一種基于瞬時相位方差加權的線譜檢測器

鄭恩明 余華兵 陳新華 孫長瑜

1 引言

由于被動聲吶不主動對外輻射信號，隱蔽性較強，一直是對水下目標進行檢測、定位、跟蹤、識別重要手段之一。但隨著隱身技術的不斷提高，被動聲吶接收數據的信噪比隨之在不斷降低，對被動聲吶的性能需求也越來越嚴格。被動聲吶常用的檢測技術 能量累積檢測方法，現已不能滿足遠程目標檢測需求。學者通過理論和實驗證明了：水下目標輻射噪聲中含有豐富的單頻分量，特別是在低頻段，螺旋槳轉動會切割水體產生低頻信號，一部分低頻分量直接以加性形式出現在目標輻射信號中，另有部分被船體自身振動調制到較高頻帶[16]-，線譜譜級通常比連續譜平均譜級高出 10～25 dB。這為被動聲吶實現水下目標遠程探測提供一種可能，也促使了線譜檢測技術的進一步發展。

依據水下目標輻射噪聲含有高強度穩定線譜這一特征，國內外學者在不同方面進行了有效、有針對性研究，提高了被動聲吶性能[715]-。文獻[9,10]提出了一種基于瞬時頻率方差加權的陣列信號處理方法，文獻[11]提出了一種基于瞬時方位方差加權的陣列信號處理方法，它們均克服了傳統線譜檢測4維顯示難點，改善了能量累積檢測法在遠程目標檢測方面的性能。文獻[12]提出了一種基于瞬時頻率方差加權的時延估計方法，文獻[13,14]提出了一種基于瞬時時延差方差加權的時延估計方法，它們均提高了互相關法在遠程目標定位方面的性能。

另外，在線譜檢測檢測方面，國內外學者做了不少研究，并取得了一定的研究成果，尤其是在相位差分補償、對齊方面[1620]-。文獻[16]利用線譜信號與背景噪聲間的時間相關半徑與相位起伏均勻性差異，提出了一種基于信號起伏相位差分對齊的相干檢測方法，抑制了背景噪聲能量干擾。文獻[17,18]利用相位起伏特性，改善了對目標的監測性能和線譜信號與背景噪聲的時間相關半徑。文獻[19]提出了一種差分二次平均修正的頻域相位補償線譜檢測方法，該方法與文獻[16]相似。同樣，文獻[20]給出了正弦信號的直接 FFT 參數估計與相位差分法對比研究結果。但這些方法均是基于相位差分一階矩信息進行相位對齊或補償來提高FFT參數估計效果，均沒有利用相位差分前后的相位方差二階矩信息。

[9-14]所提出的加權思想啟發，本文依據水下目標輻射噪聲含有高強度穩定線譜這一特征，利用目標線譜頻率單元對應瞬時相位比較穩定，背景噪聲頻率單元對應瞬時相位比較隨機的特點，提出一種基于瞬時相位方差加權的線譜檢測方法。該方法相比相位差分對齊或補償法[1620]-可以進一步增強目標線譜檢測信噪比增益，抑制背景噪聲能量干擾，實現對水下目標輻射噪聲中未知線譜的檢測。并通過理論分析和實驗結果驗證了本文方法可以進一步增強目標線譜能量、抑制噪聲、提高信噪比，在抗復雜信道檢測、識別領域具有良好的應用前景。

2 信號模型

水下目標輻射信號簡化形式可表示為[5]

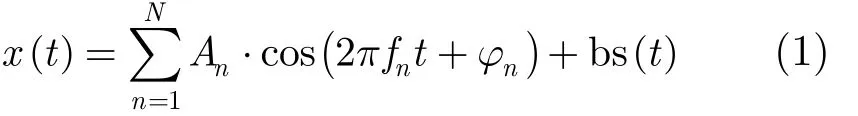
式中，nA為線譜信號幅度，nf為線譜信號頻率，nφ為線譜信號初始相位，t為目標輻射信號時刻，（）bs t為寬帶信號；N為假定的獨立分量數，nφ和（）bs t相互獨立，nφ服從[02]π～均勻分布。

以式（1）中第n個線譜信號分量為例，其與寬帶信號平均譜級比為

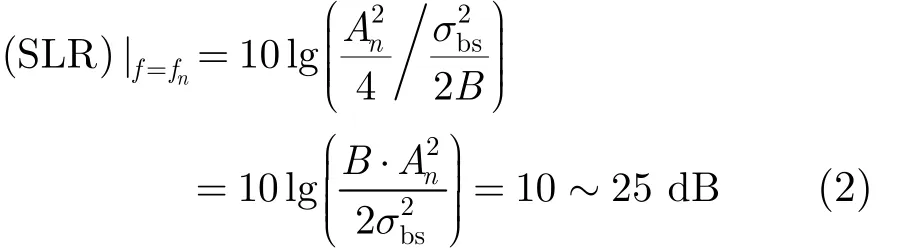
由式（2）可知，目標輻射信號的線譜信號譜級遠高于寬帶信號平均譜級。若要檢測目標，可通過檢測線譜信號來實現。

3 基于瞬時相位方差加權的線譜檢測法

由于FFT分析法處理增益較大，在檢測具有強線譜目標時，常被采用。由于背景噪聲頻譜值起伏很大，常規FFT分析法所得最終頻譜會存在線譜信號被淹沒在背景噪聲中情況，不便于線譜檢測。對此，本文對常規FFT分析法做了進一步改進處理，以增強目標線譜能量、抑制噪聲、提高信噪比。

3.1 算法基本原理

假設目標輻射信號具有穩定線譜，統計時間內線譜相位或差分相位變化緩慢，可以采用下述方法實現線譜檢測。

首先對采集數據分塊做FFT分析，所得頻譜記為X（ m, fk）,m =1,2,… ,M ,k = 1 ,2,…, K ； 其中，M為采集數據分塊數，K為每塊FFT分析所得頻率單元數。

然后對每塊 FFT分析結果所有頻率單元進行瞬時相位提取，記為φ（m, fk）,m=1,2,…,M, k=1,2,…,K。

如果采用常規FFT分析法進行線譜檢測，最終頻譜可按式（3）表示：

在濾波器頻帶 B = f1～ fK內，當目標輻射信號只占據某一個或某幾個頻率單元時，如果采用式（3）求取最終頻譜，則會將所有頻率單元對應譜值等價地加權到最終頻譜中。由于背景噪聲頻譜值起伏很大，最終頻譜受噪聲影響較大，不便于最后線譜檢測。對此，利用線譜頻率單元與噪聲頻率單元對應瞬時相位在二階矩上的差別，對各頻率單元進行加權求和，削弱噪聲對最終頻譜影響，增強線譜檢測信噪比增益，抑制背景噪聲能量干擾，可將式（3）變換為

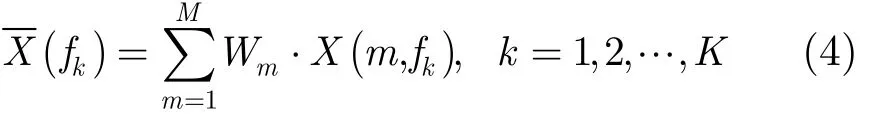
式中，mW 為不同頻率單元所需權值。

基于瞬時相位方差加權的線譜檢測流程圖如圖1 所示。

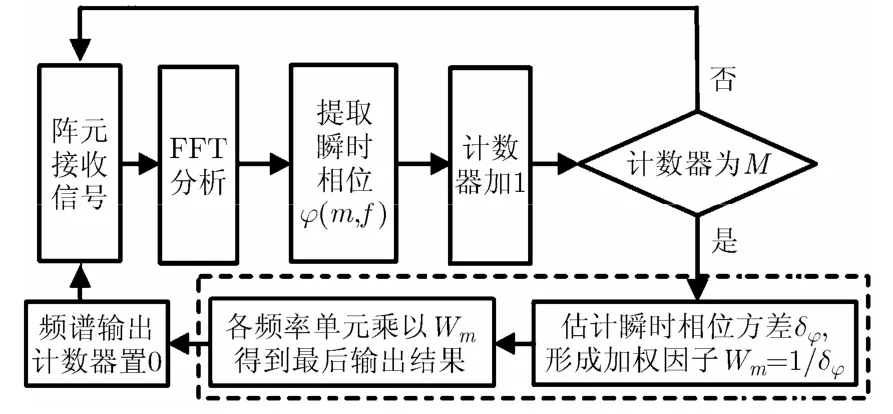
圖1 基于瞬時相位方差加權的線譜檢測流程圖

圖中虛線部分既為本文對 FFT分析法所做改進。

3.2 算法實現

依據圖1所示流程圖，本文方法實現過程可分為以下5個步驟：

步驟 1 對陣元拾取數據進行濾波放大，然后通過A/D電路采樣，采樣率為 fs，得到離散信號x（ n' Ts） ，其中，Ts=1/fs,n ' = 1 ,2,… ,N ',N'為數據長度；

步驟2 按式（5）對x（ n'Ts）做FFT分析，并提取X（ kws）中各頻率單元瞬時相位；為了充分利用所得信號，本文采用α-β濾波器得到本次所需頻譜。

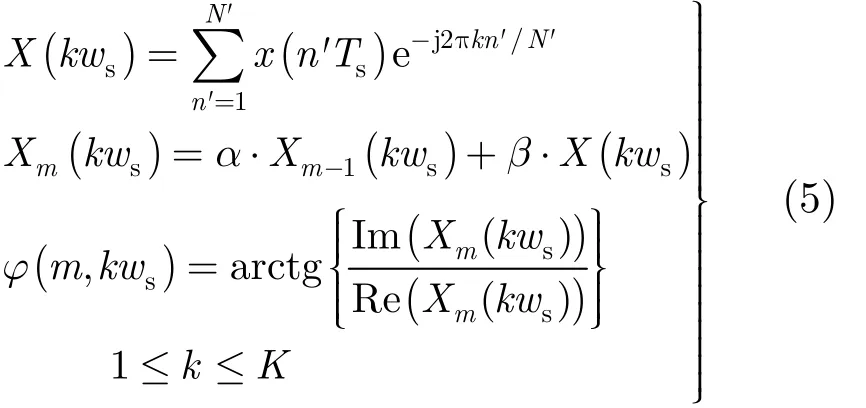
式中，ws= 2π/ KTs是FFT分析中的頻率采樣間隔。Xm（kws） 疊加了頻譜數據Xm-1（kws） ，其中，1≤m≤M ,M為統計次數，X0（kws）=0,α =β=0.5為本文所用濾波器系數；

步驟3 更新接收信號，重復進行步驟1、步驟2，直到重復次數達到預先設定值M，則各頻率單元均得到M個瞬時相位值，記為 φ （ m, kws）, m =1,2,…,M,k = 1 ,2,…, K ；

步驟 4 對所有頻率單元的瞬時相位值按式（6）進行方差計算，記為 δφ（ k ws）,k = 1 ,2,… , K 。

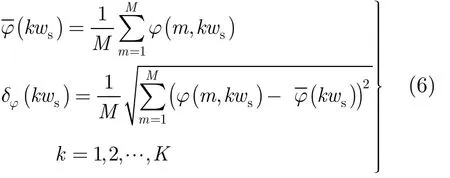
步驟 5 對所有頻率單元進行瞬時相位方差加權統計，得到最終頻譜和信號線譜估計值。如式（7）所示。

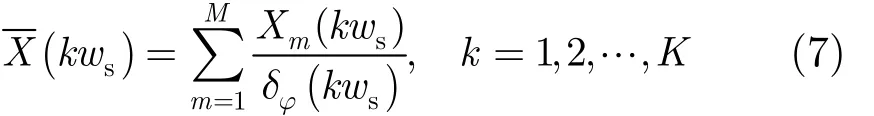
當 δφ（ k ws） 較小時，其對應頻率單元譜值在X（ kws）中數值較大，便于檢測提取。

3.3 算法性能分析

設濾波器頻帶上下限為 f1,fK，目標線譜占其中一個頻率單元。最小和最大預成瞬時相位值為φ1,φL，目標線譜頻率單元瞬時相位值的最小值和最大值分別為φmin, φmax。進行M幀統計，假設所有頻率單元瞬時相位值均服從均勻分布，背景噪聲和目標線譜瞬時相位方差分別為δn, δs。

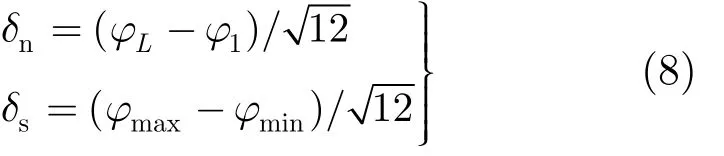
首先對背景噪聲頻率單元進行統計，對于背景噪聲頻率單元，每個預成瞬時相位值出現概率相等。

然后將目標線譜瞬時相位方差結果累加到式（9）中，可得

式（10）可簡化為

所以當目標線譜相位比較穩定被正確估計的概率在50%以上時，通過排序、提取中間部分值可使相位方差值 δs＜＜δn；當目標線譜頻率單元對應瞬時相位受水聲信道影響產生波動時，可對各頻帶瞬時相位先進行差分對齊，然后再求取相位差分對齊后的相位方差值。此時由文獻[16]可知目標線譜頻率單元對應瞬時相位差分值比較穩定，背景噪聲頻率單元對應瞬時相位差分值比較隨機，進而可得相位差分對齊后的相位方差值 δs＜＜ δn，由式（11）可知：在頻譜輸出值中，目標線譜頻率單元對應譜值將遠大于其它位置對應譜值。

依據水下目標輻射噪聲的線譜幅值明顯高出連續譜幅值。現假定目標輻射信號只有線譜分量，線譜 1，線譜 2頻率分別為69 Hz和100 Hz，干擾為帶限噪聲，帶寬為10 ～ 5 00 Hz。圖2，圖3和圖4分別是3種方法從輸入平均譜級比-30～30 dB，每個平均譜級比下做 1000次獨立統計所得線譜頻率單元與噪聲頻率單元的瞬時相位標準差和最終線譜頻率單元與噪聲頻率單元的平均譜級比，每次采集長度為 T = 1 0 s，對采集數據分10段進行FFT分析。

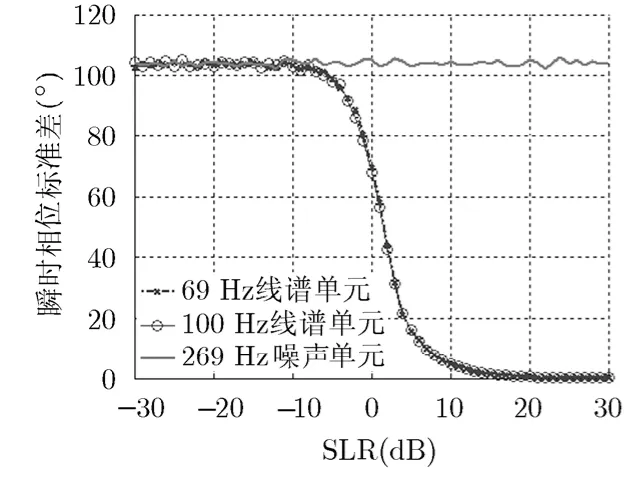
圖2 不同輸入平均譜級比下的瞬時相位標準差

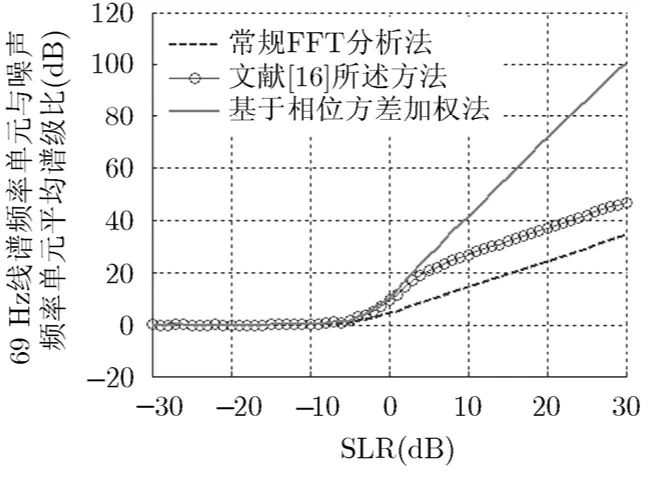
圖3 不同輸入平均譜級比下，3 種方法所得69 Hz線譜頻率單元與噪聲頻率單元平均譜級比

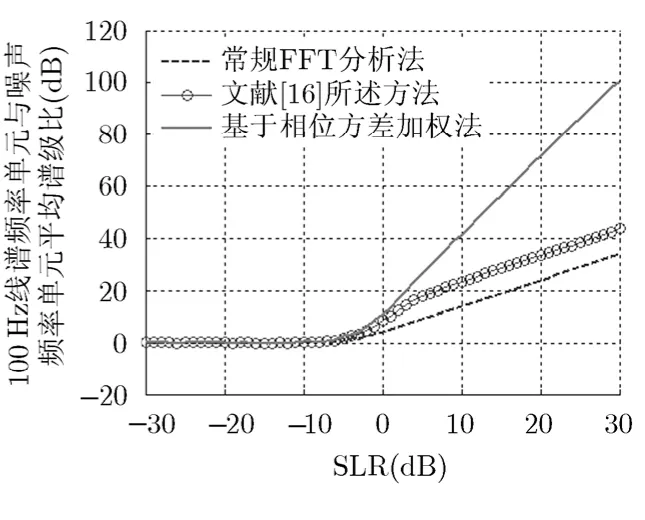
圖4 不同輸入平均譜級比下，3 種方法所得100 Hz線譜頻率單 元與噪聲頻率單元平均譜級比

由圖2可知，在輸入平均譜級比高于-6 dB時，目標線譜頻率單元瞬時相位標準差小于噪聲頻率單元的瞬時相位標準差。由圖 3 和圖4可知，相比常規FFT分析法、文獻[16]所述方法所得最終線譜頻率單元與噪聲頻率單元的平均譜級比，在輸入平均譜級比大于 6 dB- 時，本文方法所得最終線譜頻率單元與噪聲頻率單元的平均譜級比得到了提高，且隨著輸入平均譜級比越高，輸出線譜頻率單元與噪聲頻率單元的平均譜級比被提高越多。原因在于在相位存在波動時，每一時刻所得頻譜相位并非完全一致，常規FFT分析法在沒有進行相位對齊時，求得的最后頻譜并非為線譜真實幅值的絕對累加，而文獻[16]所述方法是先對每一時刻所得頻譜相位進行對齊，然后采用式（3）求取最后頻譜，所得最后頻譜為線譜真實幅值的絕對累加。所以輸入平均譜級比大于-6 dB時，文獻[16]所述方法相比常規 FFT分析法所得最后頻譜的線譜頻率單元與噪聲頻率單元的平均譜級比得到了提高；且在高信噪比下，線譜真實幅值的絕對累加與非真實幅值的絕對累加差別基本不變，所以在輸入平均譜級比大于5 dB，文獻[16]所述方法相比常規FFT分析法所得最后頻譜的線譜頻率單元與噪聲頻率單元的平均譜級比的差值基本不變。在相位存在波動時，本文方法先對每一時刻所得頻譜相位進行差分對齊，然后再求取相位方差，最后采用式（7）求取最后頻譜，由于δs＜＜δn，所得頻譜的線譜頻率單元與噪聲頻率單元的平均譜級比得到了進一步提高。在仿真情況下，輸入譜級比越高，δs越小，所得頻譜的線譜頻率單元與噪聲頻率單元的平均譜級比提高越大。

4 實驗結果

本次海試數據為2014年7月在南海進行相關海試采集存儲所得。當時海深80 m左右，海底平坦，海況3級左右。試驗所用目標船和接收設備如圖5所示，潛標所連水聽器布放于60 m深度，目標船在潛標1 km附近運動，水聽器所接采集設備采樣率為20 kHz。

圖6～圖10為一次采集長度為 5 s T= ，對采集數據分5段進行 FFT分析，然后再分別按式（3）、文獻[16]所述方法和式（7）所得最終頻譜圖、輸出線譜頻率單元與噪聲頻率單元平均譜級、瞬時相位標準差和LOFAR圖。

由圖6結果可知，相比常規FFT分析法、文獻[16]所述方法，本文方法可有效增強目標線譜能量、抑制噪聲、提高信噪比；在t=300 s數據段中，本文方法相比文獻[16]所述方法所得 69 Hz處線譜頻率單元平均譜級提高了近7 dB, 107 Hz處線譜頻率單元平均譜級提高了近 14 dB；本文方法相比常規FFT分析法所得69 Hz處線譜頻率單元平均譜級提高了近5 dB, 107 Hz處線譜頻率單元平均譜級提高了近12 dB。原因可由圖7得，在大部分時間段內，δs＜＜ δn，經式（7）處理后，所得頻譜的線譜頻率單元譜級相比噪聲頻率單元譜級被有效擴大，所以可得在其他時間數據段中，本文方法相比常規FFT分析法、文獻[16]所述方法在69 Hz, 107 Hz處線譜頻率單元平均譜級提高更多。

同樣，對比圖 8至圖10可知，常規FFT分析法已不能檢測到 69 Hz處目標線譜信號，文獻[16]所述方法雖然能檢測到69 Hz處目標線譜信號，但與背景噪聲譜級差別不大，而本文方法可以有效檢測到69 Hz處線譜頻率單元信號，且與背景噪聲譜級差別較大；且對于107 Hz處線譜頻率單元信號的檢測效果，本文方法遠好于FFT法分析法、文獻[16]所述方法。

5 結束語

本文依據水下目標輻射噪聲含有高強度穩定線譜這一特征，介紹了一種基于瞬時相位方差加權的線譜檢測方法。本文方法首先對接收信號做FFT，然后對所有頻率單元均進行瞬時相位提取，利用目標線譜頻率單元對應瞬時相位比較穩定，背景噪聲頻率單元對應瞬時相位比較隨機的特點，對各頻率單元進行瞬時相位方差加權統計，進一步抑制了背景噪聲能量干擾，增強了目標線譜檢測信噪比增益。在本文仿真條件下，相比常規FFT分析法、相位差分對齊法[16]所得最終線譜頻率單元與噪聲頻率單元的平均譜級比，在輸入平均譜級比大于-6 dB時，本文方法所得最終線譜頻率單元與噪聲頻率單元的平均譜級比得到了進一步提高，且隨著輸入平均譜級比越高，輸出線譜頻率單元與噪聲頻率單元的平均譜級比提高越多。海試數據處理結果同樣驗證了本文所提方法相比常規FFT分析法、相位差分對齊法，進一步抑制了背景噪聲能量干擾，增強了目標線譜檢測信噪比增益，實現了對水下目標輻射噪聲中未知線譜的檢測。另外，在目標線譜頻率單元對應瞬時相位受水聲信道影響產生波動時，可對各頻帶瞬時相位先進行差分對齊，然后再求取相位差分對齊后的相位方差值。

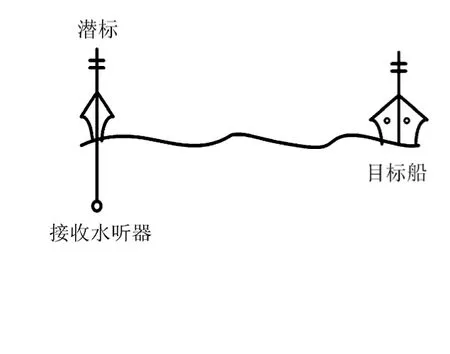
圖5 海試試驗系統圖

圖6 3種方法所得最終頻譜圖（t=300 s）

圖7 瞬時相位標準差

圖8 常規FFT分析法所得最終LOFAR圖

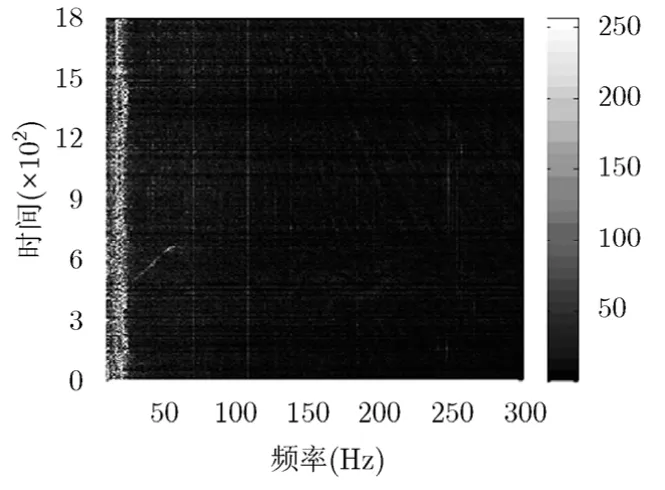
圖9 文獻[16]所示方法所得 最終LOFAR圖

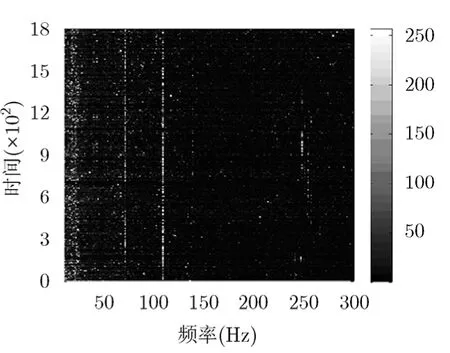
圖10 基于瞬時相位方差加 權法所得最終LOFAR圖

參 考 文 獻

[1] Urick R J. Principles of Underwater Sound[M]. New York:McGraw-Hill Book Company, 1983: 61-79.

[2] Ross D. Mechanics of Underwater Noise[M]. New York:Pergmin Press, 1976: 83-89.

[3] Crocker S E, Nielesen P L, Miller J H, et al.. Geoacoustic inversion of ship radiated noise in shallow water using data from a single hydrophone[J]. Journal of the Acoustical Society of America, 2014, 136（5）: 362-368.

[4] Megan F, Donald R, and Sean M. Underwater radiated noise from modern commercial ships[J]. Journal of the Acoustical Society of America, 2012, 131（1）: 92-103.

[5] 李啟虎, 李敏, 楊秀庭. 被動目標輻射噪聲中單頻信號分量的檢測: 理論分析[J]. 聲學學報, 2008, 33（3）: 193-196.Li Qi-hu, Li Min, and Yang Xiu-ting. The detection of single frequency component of underwater radiated noise of target:theoretical analysis[J]. Acta Acustica, 2008, 33（3）: 193-196.

[6] 李啟虎, 李敏, 楊秀庭. 被動目標輻射噪聲中單頻信號分量的檢測: 數值仿真[J]. 聲學學報, 2008, 33（4）: 289-293.Li Qi-hu, Li Min, and Yang Xiu-ting. The detection of single frequency component of underwater radiated noise of target:digital simulation[J]. Acta Acustica, 2008, 33（4）: 289-293.

[7] Tucker J D and Azimi-Sadjadi M R. Coherence-based underwater target detection from multiple disparate sonar platforms[J]. IEEE Journal of Oceanic Engineering, 2011,36（1）: 37-51.

[8] 吳國清, 王美剛, 陳耀明. 水聲波導中包絡線譜強度數值預報[J]. 聲學學報, 2013, 37（4）: 432-439.Wu Guo-qing, Wang Mei-gang, and Chen Yao-ming.Numerical prediction of envelope line spectrum intensity in underwater acoustic waveguide[J]. Acta Acustica, 2013, 37（4）:432-439.

[9] 陳陽, 王自娟, 朱代柱, 等. 一種基于頻率方差加權的線譜目標檢測方法[J]. 聲學學報, 2010, 35（1）: 76-80.Chen Yang, Wang Zi-juan, Zhu Dai-zhu, et al.. A detecting method for line-spectrum target based on variance of frequency weight[J]. Acta Acustica, 2010, 35（1）: 76-80.

[10] 陳陽, 趙安邦, 王自娟, 等. 瞬時頻率方差加權導向最小方差波束形成檢測器[J]. 哈爾濱工程大學學報, 2011, 32（6）:730-735.Chen Yang, Zhao An-bang, Wang Zi-juan, et al.. Variance of instantaneous frequency-weighted steered minimum variance beamforming detector[J]. Journal of Harbin Engineering University, 2011, 32（6）: 730-735.

[11] 陳新華, 鮑習中, 李啟虎, 等. 水下聲信號未知頻率的目標檢測方法研究[J]. 兵工學報, 2012, 33（4）: 471-475.Chen Xin-hua, Bao Xi-zhong, Li Qi-hu, et al.. Research on detection of underwater acoustic signal with unknown frequency[J]. Acta Armamentarii, 2012, 33（4）: 471-475.

[12] 鄭恩明, 陳新華, 孫長瑜. 基于頻率方差加權的時延差估計方法[J]. 系統工程與電子技術, 2014, 36（2）: 224-229.Zheng En-ming, Chen Xin-hua, and Sun Chang-yu. The time delay difference estimation weighted method based on frequency variance[J]. Systems Engineering and Electronics,2014, 36（2）: 224-229.

[13] 鄭恩明, 陳新華, 孫長瑜, 等.基于時延差方差加權的時延差估計方法[J]. 電子與信息學報, 2014, 36（6）: 1362-1367.Zheng En-ming, Chen Xin-hua, Sun Chang-yu, et al..Weighted time delay difference estimation method based on Its variance[J]. Journal of Electronics & Information Technology, 2014, 36（6）: 1362-1367.

[14] 鄭恩明, 陳新華, 孫長瑜. 一種水下聲信號未知頻率的時延差估計方法[J]. 振動與沖擊, 2014, 33（9）: 190-194.Zheng En-ming, Chen Xin-hua, and Sun Chang-yu. A time delay difference estimation method of underwater acoustic sgnal with unknown frequency[J]. Journal of Vibration and Shock, 2014, 33（9）: 190-194.

[15] 張建, 關鍵, 董云龍, 等. 基于局部 Hilbert 譜平均帶寬的微弱目標檢測算法[J]. 電子與信息學報, 2012, 34（1）: 121-127.Zhang Jian, Guan Jian, Dong Yun-long, et al.. Weak target detection based on the average bandwidth of the partial hilbert spectrum[J]. Journal of Electronics & Information Technology, 2012, 34（1）: 121-127.

[16] 解愷, 丁雪潔, 孫貴青, 等. 基于目標輻射噪聲的信號起伏檢測算法研究[J]. 電子與信息學報, 2013, 35（4）: 844-851.Xie Kai, Ding Xue-jie, Sun Gui-qing, et al.. The signal fluctuating detection algorithm based on the target radiated noise[J]. Journal of Electronics & Information Technology,2013, 35（4）: 844-851.

[17] Venugopal S, Wagstaff R A, and Sharma J P. Exploiting phase fluctuations to improve machine performance monitoring[J]. IEEE Transactions on Automation Science and Engineering, 2007, 4（2）: 153-166.

[18] Wagstaff R A. Exploiting phase fluctuations to improve temporal coherence[J]. IEEE Journal of Oceanic Engineering,2004, 29（2）: 498-510.

[19] 戴文舒, 陳亞, 陳新華, 等. 差分二次平均修正的頻域相位補償線譜檢測方法[J]. 兵工學報, 2014, 35（10）: 1630-1637.Dai Wen-shu, Chen Ya, Chen Xin-hua, et al.. An algorithm of line-spectrum detection uUsing frequency domain phase compensation with difference and TPM technique[J]. Acta Armamentarii, 2014, 35（10）: 1630-1637.

[20] 李輝, 王巖飛. 正弦信號的直接 FFT 參數估計與相位差分法對比研究[J]. 電子與信息學報, 2010, 32（3）: 544-547.Li Hui and Wang Yan-fei. The contrastive study between direct FFT and phase difference in parameter estimation of sinusoidal signal[J]. Journal of Electronics & Information Technology, 2010, 32（3）: 544-547.