利用等差數(shù)列構(gòu)造大圍長(zhǎng)準(zhǔn)循環(huán)低密度奇偶校驗(yàn)碼
張 軼 達(dá)新宇 蘇一棟
1 引言
碼的結(jié)構(gòu)決定了低密度奇偶校驗(yàn)(Low-Density Parity-Check, LDPC)碼的性能。基于循環(huán)移位矩陣構(gòu)造的準(zhǔn)循環(huán)低密度奇偶檢驗(yàn)(Quasi-Cyclic Low-Density Parity-Check, QC-LDPC)碼,其校驗(yàn)矩陣的準(zhǔn)循環(huán)特性使其易于高效編解碼,碼的代數(shù)結(jié)構(gòu)為超大規(guī)模集成電路的實(shí)現(xiàn)提供了可能,因此受到廣泛關(guān)注和研究。圍長(zhǎng)是碼中最小的環(huán)長(zhǎng)度,增大圍長(zhǎng)可以提高碼字的性能。借助于計(jì)算機(jī)搜索,人們已經(jīng)提出了一些圍長(zhǎng)大于6的QC-LDPC碼構(gòu)造方法[17]-,但為了滿足各種約束條件,這些準(zhǔn)隨機(jī)方法通常花費(fèi)時(shí)間長(zhǎng),存在失敗可能,且對(duì)編解碼存儲(chǔ)空間提出了更高要求。
針對(duì)上述問題,國(guó)內(nèi)外學(xué)者對(duì)確定性構(gòu)造方法的研究屢有成果涌現(xiàn)。文獻(xiàn)[8]和文獻(xiàn)[9]分別采用群結(jié)構(gòu)法、3維循環(huán)網(wǎng)絡(luò)法構(gòu)造出了圍長(zhǎng)在10以上的QC-LDPC碼,但是校驗(yàn)矩陣的行重只局限于特定范圍內(nèi);文獻(xiàn)[10-12]基于貪婪算法構(gòu)造了圍長(zhǎng)為 8的QC-LDPC碼,其循環(huán)移位矩陣尺寸具有連續(xù)變化的優(yōu)點(diǎn),但該方法要求準(zhǔn)循環(huán)基矩陣首行首列元素必須為0;文獻(xiàn)[13]提出了基于二次函數(shù)的確定性方法,但方程系數(shù)與行重有關(guān),任意行重只能構(gòu)造兩種校驗(yàn)矩陣。這在一定程度上限制了它們的實(shí)際應(yīng)用。
在此基礎(chǔ)上,本文利用等差數(shù)列提出一種列重為3、圍長(zhǎng)至少為8的 QC-LDPC碼構(gòu)造方法。首先通過舉例歸納得到約束條件,總結(jié)出推導(dǎo)思路和方法;然后將特殊情形推廣,進(jìn)而提出基于一般等差數(shù)列的確定性構(gòu)造方法,并證明了其圍長(zhǎng)特性;最后通過軟件仿真,驗(yàn)證了該方法構(gòu)造的 QC-LDPC碼參數(shù)設(shè)置靈活、性能優(yōu)良。
2 QC-LDPC碼
QC-LDPC碼是一類非常特殊的高度結(jié)構(gòu)化的LDPC碼,它的校驗(yàn)矩陣以單位陣的循環(huán)移位陣和零方陣為子陣,可表示為
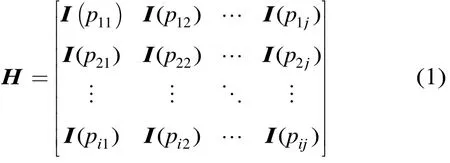
其中: I (pij)表示一個(gè)p×p的循環(huán)移位矩陣,pij∈{0,1,2,… ,p -1,∞ }。易知I(0)就是單位陣Ip×p,零方陣用I(∞)表示。把循環(huán)右移系數(shù)pij寫成一個(gè)矩陣P,稱為準(zhǔn)循環(huán)基矩陣,如式(2)所示[14]。當(dāng)P確定后,校驗(yàn)矩陣H也隨之確定。
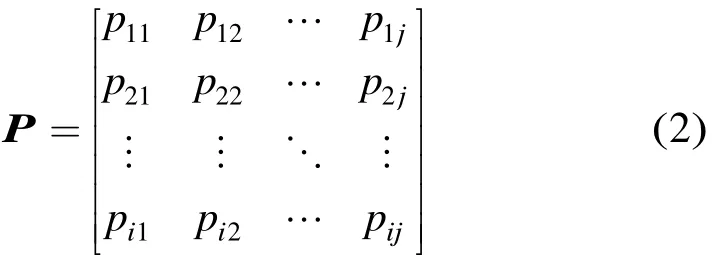
在基矩陣P中,若干個(gè)點(diǎn)(元素)p1,p2,… , p2k構(gòu)成一個(gè)環(huán),則對(duì)應(yīng)的H矩陣也存在與之對(duì)應(yīng)的p個(gè)同樣大小的環(huán)。顯然,環(huán)的長(zhǎng)度只能是大于或等于4的偶數(shù)。表示H中長(zhǎng)為2k環(huán)的序列(p1, p2,…,p2k)滿足定理1。
定理 1[15]對(duì)于基矩陣 P中的序列(p1, p2,… ,p2k),其中 pi和 pi+1在同一行或同一列,pi和 pi+2在不同行且不同列,則(p1, p2,… , p2k)構(gòu)成長(zhǎng)為2k環(huán)的充分必要條件是
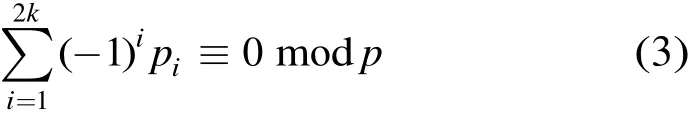
短環(huán)的存在使 LDPC碼在譯碼時(shí)不能快速收斂,甚至不能收斂,造成誤比特率(Bit Error Rate,BER)性能變差。因此,為了使校驗(yàn)矩陣不含長(zhǎng)為2k的環(huán),就必須通過某種設(shè)計(jì),使得式(3)不成立。圖1給出了6環(huán)存在的6種形狀。
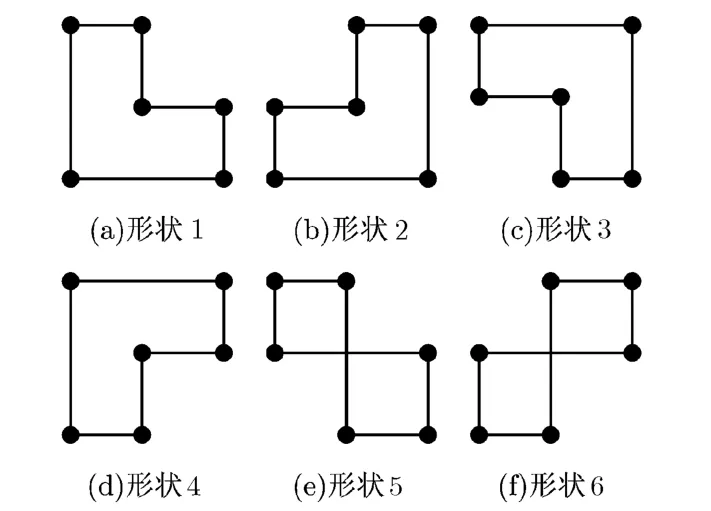
圖1 6種形狀的6環(huán)
3 基于等差數(shù)列的確定性構(gòu)造
3.1 歸納推導(dǎo)
對(duì)列重為3的校驗(yàn)矩陣的基矩陣采取的配置方式為
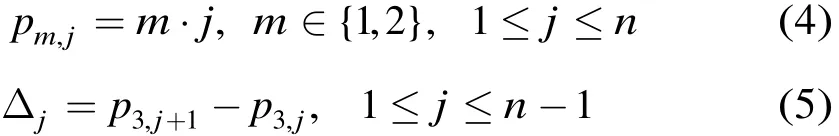
其中n為基矩陣的列數(shù)。顯然,此時(shí) { p1,j}為正整數(shù)列, { p2,j}為正偶數(shù)列。對(duì) p3,2進(jìn)行賦值時(shí),為避免出現(xiàn)短環(huán),則Δ1應(yīng)滿足:
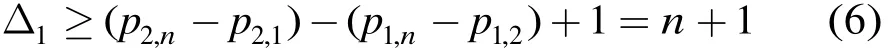
依此類推,可以得到滿足圍長(zhǎng)至少為8的{Δj} 的取值下界,如表1所示。

表1 n69=~時(shí)j{}Δ的取值下界

3.2 構(gòu)造方法
上節(jié)的結(jié)論是基于一種特例推導(dǎo)給出的。若采取相同的分析方法,將式(4)推廣至一般等差數(shù)列,則得到一種(3,)n基矩陣的構(gòu)造方法為
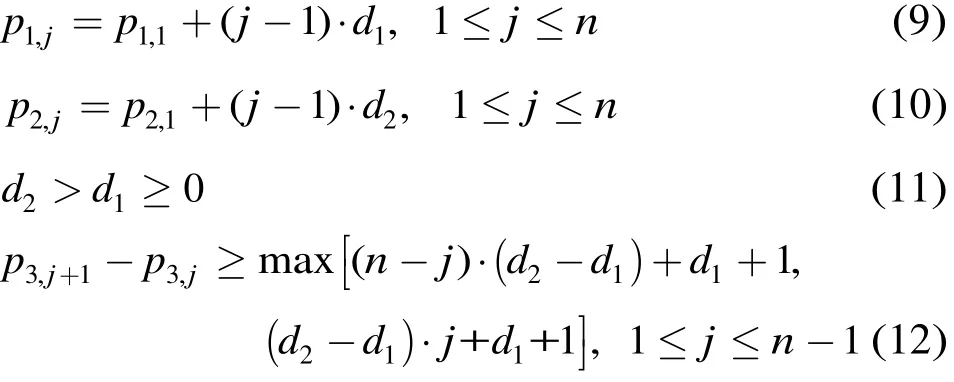
其中1d,2d分別為兩個(gè)等差數(shù)列的公差。
4 圍長(zhǎng)至少為8的性質(zhì)證明
定理2 對(duì)于任意 n ≥ 3 ,滿足式(9)~式(12)定義的基矩陣P的圍長(zhǎng)至少為8。
證明 圍長(zhǎng)至少為8即不存在4環(huán)和6環(huán)。
(1)4環(huán)檢驗(yàn) 不失一般性,令1 ≤ s <t ≤ n 。若P中存在4環(huán),則滿足式(13)中的至少一項(xiàng)
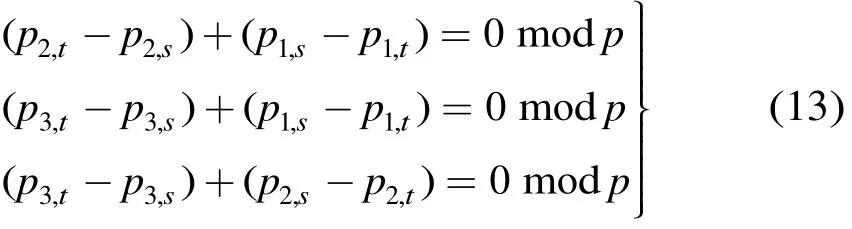
這是不可能的,因?yàn)楫?dāng)n為奇數(shù)時(shí),
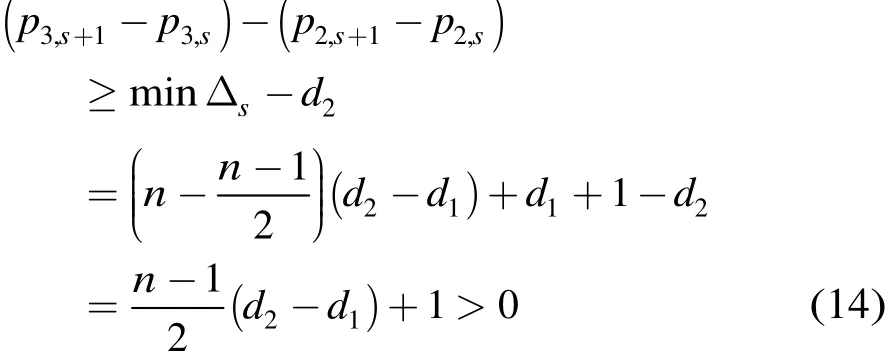
當(dāng)n為偶數(shù)時(shí),同理可得
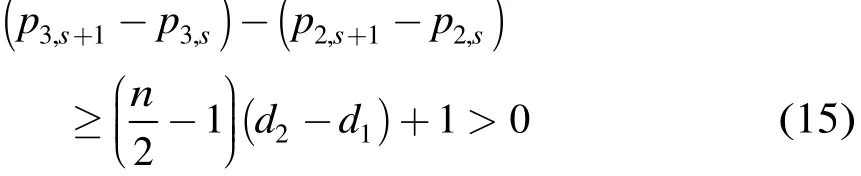
因此有
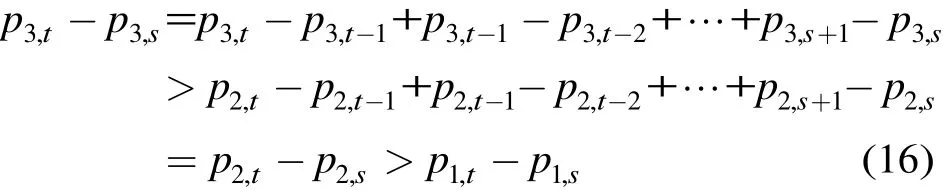
注意到 0 < p3,s- p3,t<p 和 0 < p2,s- p2,t< p ,故式(13)不成立。因此,P中不存在4環(huán)。
(2)6環(huán)檢驗(yàn) 不失一般性,令1 ≤ i < k <j ≤ n。若P中存在圖1(a)所示6環(huán),則
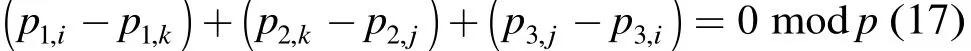
這是不可能的,因?yàn)橛?環(huán)檢驗(yàn)的結(jié)論,有

故式(17)不成立,同理可證P中也不存在圖1(b)~圖1(d)所示6環(huán)。
下面考慮圖1(e)的情形:
若 j - k = 1 ,由式(12)可得 p3,j-p3,k≥(d2-d1)?k+d1+1,故
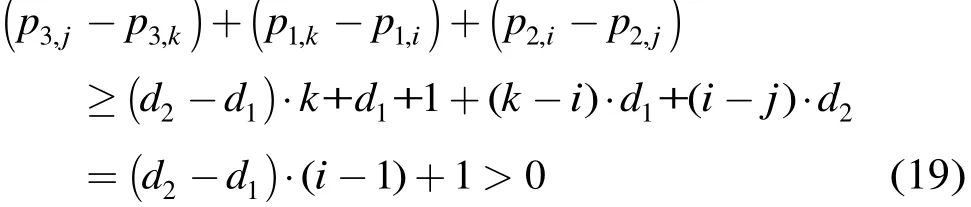
若 j - k ≥ 2 ,以 n為奇數(shù)為例(偶數(shù)時(shí)同理),由 { p3,j}為單增數(shù)列可得
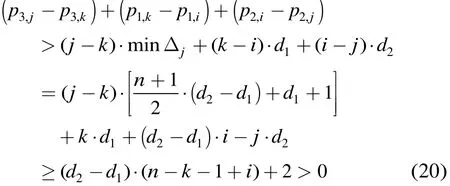
因此P中不存在圖1(e)所示6環(huán),同理也不存在圖1(f)所示6環(huán)。
綜上,基矩陣P的圍長(zhǎng)至少為8。 證畢
利用等差數(shù)列求和公式可求出3,np 的通項(xiàng)表達(dá)式。
當(dāng)n為奇數(shù)時(shí),
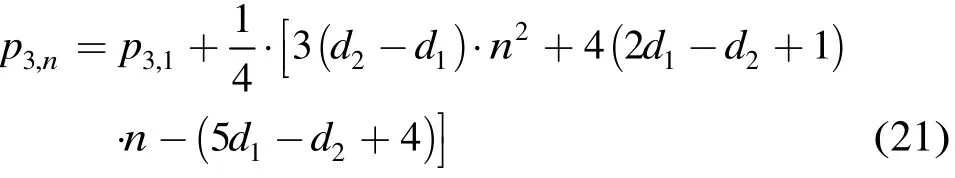
當(dāng)n為偶數(shù)時(shí),
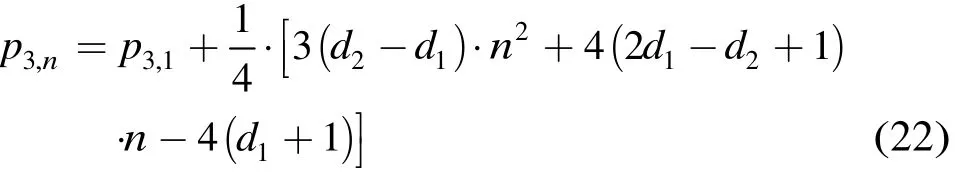
可以發(fā)現(xiàn),當(dāng)3,1p ,1d,2d確定后,3,np 是關(guān)于n的二次函數(shù)。由于本文方法中參數(shù)設(shè)置的靈活性,而移位矩陣的維數(shù)p大于移位系數(shù),故p的取值下界為
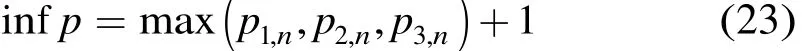
特別地,當(dāng) p1,1= p2,1= p3,1= d1= 0 , d2= 1 時(shí),式(21)的計(jì)算結(jié)果為 3 (n2- 1 )/4,式(22)為 3 n2/4 - 1,此時(shí)p的下界為 3 n2/4,與文獻(xiàn)[10]給出的研究結(jié)果相一致,說明該基矩陣是本文方法的一種特例。
5 仿真與分析
5.1 p值下界分析
構(gòu)造3種準(zhǔn)循環(huán)基矩陣,設(shè) di= i , i ∈ { 1,2},其它參數(shù)如表2所示。圖2描繪了這3種碼字p的取值下界隨n的變化曲線。
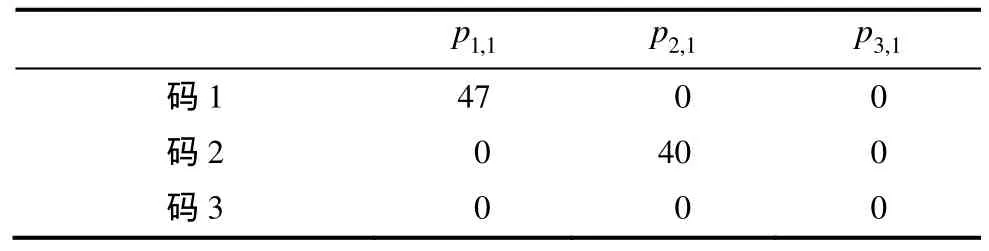
表2 d i = i , i ∈ { 1,2}時(shí)的參數(shù)配置
從圖2中可以看到,p的取值下界隨n的增大而增大。當(dāng)3≤n<8時(shí),碼1、碼2的p值下界與n呈線性關(guān)系,當(dāng) n ≥ 8 時(shí),3條曲線重合,此時(shí)p的取值僅與 p3,n有關(guān)。這是因?yàn)?種基矩陣的 { p3,j}完全一致,且由式(16)可知, { p3,j}中元素的增幅顯然大于 { p1,j}和{p2,j},隨著n的增大,無(wú)論初始參數(shù)如何設(shè)置, in f p = p3,n+ 1都是必然結(jié)果。同時(shí)表明,利用本文方法構(gòu)造的任意參數(shù)的準(zhǔn)循環(huán)基矩陣,都可使p值獲得連續(xù)取值的下界。
5.2 圍長(zhǎng)分析
構(gòu)造3種準(zhǔn)循環(huán)基矩陣,設(shè) n = 6 ,其它參數(shù)如表3所示。圖3描繪了這3種碼字的8環(huán)數(shù)目隨p值的變化曲線,圖4為碼長(zhǎng)一定(N = n ? p= 9 60)條件下,碼3的8環(huán)數(shù)目隨n的變化曲線。可以看到,基矩陣一定時(shí)8環(huán)數(shù)隨p值增大而增多;而當(dāng)碼長(zhǎng)一定時(shí),p值越小則行重越大,意味著形成短環(huán)的概率越大,造成環(huán)數(shù)增多。因此在構(gòu)造基矩陣時(shí),針對(duì)不同的編碼參數(shù)需求,本文方法提供了一種簡(jiǎn)單、靈活的設(shè)計(jì)思路。
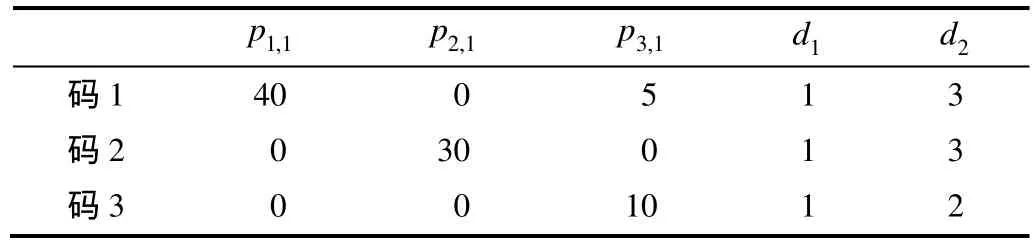
表3 n 6= 時(shí)的參數(shù)配置
5.3 性能分析
構(gòu)造兩種準(zhǔn)循環(huán)基矩陣,設(shè)碼率 1/2R= ,其它參數(shù)如表 4所示。在加性高斯白噪聲(Additive White Gauss Noise, AWGN)信道下進(jìn)行仿真,譯碼采用置信傳播(Belief Propagation, BP)算法,最大迭代次數(shù)為30,調(diào)制方式為BPSK,選取同碼長(zhǎng)碼率的漸進(jìn)邊增長(zhǎng)(Progressive Edge-Growth,PEG)[16]碼進(jìn)行性能比較。仿真結(jié)果如圖5所示。

表4 R 1/2= 時(shí)的參數(shù)配置
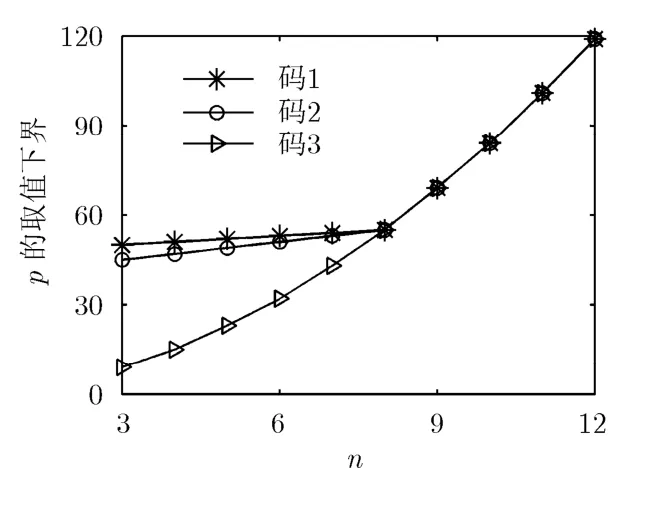
圖2 p的取值下界隨n的變化曲線
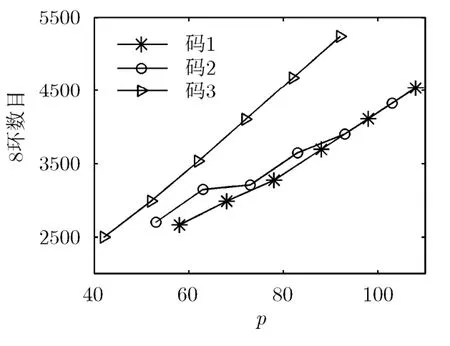
圖3 8環(huán)數(shù)目隨p值的變化曲線
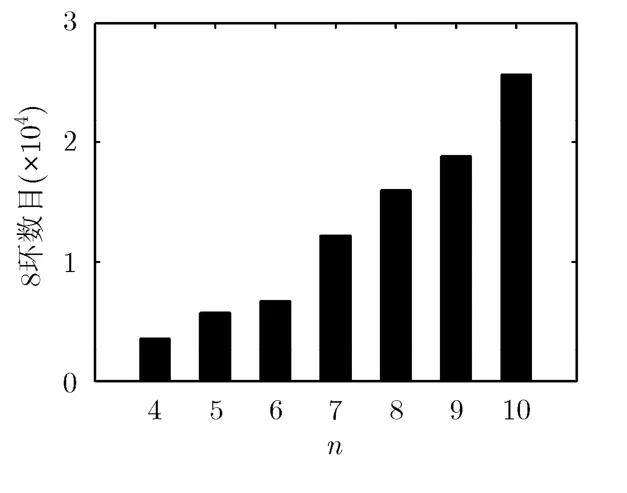
圖4 碼長(zhǎng)一定時(shí)8環(huán)數(shù)目隨n的變化曲線
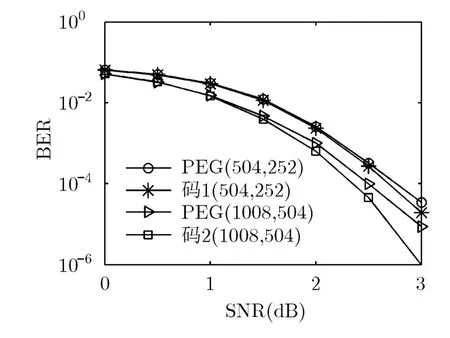
圖5 本文構(gòu)造碼字與PEG碼的性能比較
仿真結(jié)果表明,碼長(zhǎng)為504時(shí)二者的譯碼性能差異不大;當(dāng)碼長(zhǎng)為1008, BER為10-5時(shí),與PEG碼相比本文構(gòu)造碼字信噪比增益約為0.3 dB。此外,PEG方法需要對(duì)度數(shù)的分布進(jìn)行優(yōu)化處理,其算法復(fù)雜度也高于本文方法。
6 結(jié)束語(yǔ)
本文提出了一種構(gòu)造圍長(zhǎng)至少為 8的(3,)nQC-LDPC碼的確定性方法。該碼的準(zhǔn)循環(huán)基矩陣由等差數(shù)列生成的數(shù)學(xué)表達(dá)式確定,構(gòu)造方法簡(jiǎn)單,節(jié)省了編解碼存儲(chǔ)空間。研究結(jié)果表明,這類碼只需少量的初始值控制就可設(shè)計(jì)任意參數(shù)的基矩陣,同時(shí)在AWGN信道中能夠獲得較好的糾錯(cuò)能力,因此對(duì)信道編碼理論的研究和應(yīng)用具有一定的參考價(jià)值。在此方法基礎(chǔ)上,如何消除8環(huán),從而構(gòu)造圍長(zhǎng)為10的QC-LDPC碼是今后深入研究的內(nèi)容之一。
[1] O’Sullivan M E. Algebraic construction of sparse matrices with large girth[J]. IEEE Transactions on Information Theory, 2006, 52(2): 718-727.
[2] Milenkovic O, Kashyap N, and Leyba D. Shortened array codes of large girth[J]. IEEE Transactions on Information Theory, 2006, 52(8): 3707-3722.
[3] Jiang X and Lee M H. Large girth non-binary LDPC codes based on finite fields and Euclidean geometries[J]. IEEE Signal Processing Letters, 2009, 16(6): 521-524.
[4] Huang Jen-fa, Huang Chun-ming, and Yang Chao-chin.Construction of one-coincidence sequence quasi-cyclic LDPC codes of large girth[J]. IEEE Transactions on Information Theory, 2012, 58(3): 1825-1836.
[5] Zhang Guo-hua, Sun Rong, and Wang Xin-mei. Construction of girth-eight QC-LDPC codes from greatest common divisor[J]. IEEE Communications Letters, 2013, 17(2):369-372.
[6] Park H, Hong S, NO J S, et al.. Design of multiple-edge protographs for QC LDPC codes avoiding short inevitable cycles[J]. IEEE Transactions on Information Theory, 2013,59(7): 4598-4614.
[7] Mohammad G and Ghaffar R. Column weight two and three LDPC codes with high rates and large girths[OL].http://arxiv.org/abs/1403.6090, 2014.4.
[8] Kim S, NO J S, Chung H, et al.. On the girth of tanner (3, 5)quasi-cyclic LDPC codes[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1739-1744.
[9] Zhang Fan, Mao Xue-hong, Zhou Wu-yang, et al.. Girth- 10 LDPC codes based on 3-D cyclic lattices[J]. IEEE Transactions on Vehicular Technology, 2008, 57(2):1049-1060.
[10] 張國(guó)華, 陳超, 楊洋, 等. Girth-8 (3, L)-規(guī)則QC-LDPC碼的一種確定性構(gòu)造方法[J]. 電子與信息學(xué)報(bào), 2010, 32(5):1152-1156.Zhang Guo-hua, Chen Chao, Yang Yang, et al.. Girth-8 (3,L)-regular QC-LDPC codes based on novel deterministic design technique[J]. Journal of Electronics & Information Technology, 2010, 32(5): 1152-1156.
[11] Zhang Guo-hua, Sun Rong, and Wang Xin-mei. Several explicit constructions for (3, L) QC-LDPC codes with girth at least eight[J]. IEEE Communications Letters, 2013, 17(9):1822-1825.
[12] 張國(guó)華, 孫蓉, 王新梅. 圍長(zhǎng)為8的QC-LDPC碼的顯示構(gòu)造及其在 CRT方法中的應(yīng)用[J]. 通信學(xué)報(bào), 2012, 33(3):171-176.Zhang Guo-hua, Sun Rong, and Wang Xin-mei. Explicit construction of girth-eight QC-LDPC codes and its application in CRT method[J]. Journal of Communications,2012, 33(3): 171-176.
[13] Zhang Guo-hua, Sun Rong, and Wang Xin-mei. Deterministic construction of girth-eight (3, L) QC-LDPC codes from quadratic function[J]. Electronics Letters, 2013, 49(9):600-602.
[14] 楊民, 張文彥, 鐘杰, 等. 準(zhǔn)循環(huán)多進(jìn)制 LDPC碼構(gòu)造[J]. 電子與信息學(xué)報(bào), 2013, 35(2): 297-302.Yang Min, Zhang Wen-yan, Zhong Jie, et al.. Construction of non-binary QC-LDPC codes[J]. Journal of Electronics &Information Technology, 2013, 35(2): 297-302.
[15] Fossorier M P C. Quasi-cyclic low-density parity-check codes from circulant permutation matrices[J]. IEEE Transactions on Information Theory, 2004, 50(8): 1788-1793.
[16] Hu Xiao-yu, Eleftheriou E, and Amold D M. Progressive edge-growth tanner graphs[C]. Proceedings of the IEEE Global Telecommunications Conference, San Antonio, USA,2001: 995-1001.

