低輪FOX64算法的零相關(guān)-積分分析
郭 瑞 金晨輝
1 引言
目前,對(duì)分組密碼算法的攻擊方法主要分為:差分密碼分析[1]及其推廣、線性密碼分析[2]及其推廣、積分攻擊、密鑰相關(guān)攻擊、中間相遇攻擊、插值攻擊等。其中,差分密碼分析和線性密碼分析是目前對(duì)分組密碼算法安全性分析的最重要和最有效的工具。最近,文獻(xiàn)[3]提出了零相關(guān)線性分析,該分析方法基于相關(guān)系數(shù)為0的線性逼近,并通常被看作與不可能差分分析相對(duì)應(yīng)的一類推廣的線性密碼分析方法。
文獻(xiàn)[3]提出零相關(guān)線性分析方法時(shí),給出了AES算法、Skipjack算法、CAST256算法、CLEFIA算法相關(guān)系數(shù)為0的線性逼近,并成功攻擊了低輪AES-192, AES-256以及CLEFIA-256。但是,為了判斷選取的線性逼近的相關(guān)系數(shù)是否為 0,零相關(guān)線性分析需要選取明文規(guī)模至少為分組規(guī)模一半。因此,攻擊所需數(shù)據(jù)復(fù)雜度較高是零相關(guān)線性分析最大的缺陷。隨后,文獻(xiàn)[4]證明了使用多個(gè)獨(dú)立的零相關(guān)線性逼近可以降低數(shù)據(jù)復(fù)雜度。但是,多個(gè)線性逼近相互獨(dú)立的假設(shè)難以滿足。為此,文獻(xiàn)[5]指出可以使用不同的已知明文來消除線性逼近互相獨(dú)立的假設(shè),從而降低攻擊所需的數(shù)據(jù)復(fù)雜度,并給出了零相關(guān)線性區(qū)分器與積分區(qū)分器、多維線性區(qū)分器的關(guān)系。證明了由積分區(qū)分器可以得到零相關(guān)線性逼近區(qū)分器、由零相關(guān)線性逼近區(qū)分器在一定條件下同樣可以得到積分區(qū)分器,證明了零相關(guān)線性區(qū)分器是多維線性區(qū)分器的特例。同時(shí),首次給出了變形的31輪Skipjack算法的零相關(guān)-積分攻擊。此外,文獻(xiàn)[6]還給出了LBlock算法的多維-零相關(guān)線性分析,且攻擊結(jié)果的時(shí)間復(fù)雜度優(yōu)于已有攻擊結(jié)果。
本文分析 FOX系列分組密碼算法抵抗零相關(guān)線性分析的能力。FOX分組密碼算法是文獻(xiàn)[7]為了滿足Mediacrypt公司的需求而設(shè)計(jì),包括分組規(guī)模為64 bit和128 bit兩類算法,通常稱為FOX64和FOX128。FOX系列分組密碼算法的安全性基于Lai-Massey模型[8,9]的可證明安全結(jié)論,其圈函數(shù)采用嵌套 SPS結(jié)構(gòu)的 Lai-Massey模型,密鑰規(guī)模 k滿足0256k≤≤,且是8的倍數(shù)。特別地,F(xiàn)OX算法使用了復(fù)雜的密鑰編排算法,使得其由若干子密鑰無法獲取種子密鑰或其它子密鑰。已有對(duì)FOX算法有效的攻擊包括碰撞-積分攻擊、不可能差分分析、差分碰撞攻擊等。文獻(xiàn)[10]利用FOX算法的3輪區(qū)分器及碰撞技術(shù)對(duì)4, 5, 6, 7輪FOX64分析的時(shí)間復(fù)雜度分別為245.4, 2109.4, 2173.4, 2237.4,數(shù)據(jù)復(fù)雜度為29個(gè)選擇明文。文獻(xiàn)[11]和文獻(xiàn)[12]獨(dú)立地找到了4輪FOX算法的不可能差分對(duì)應(yīng),并指出不可能差分攻擊對(duì)5, 6, 7輪FOX64的時(shí)間復(fù)雜度分別為269, 2133, 2197,攻擊的數(shù)據(jù)復(fù)雜度大約為 239個(gè)選擇明文。此外,文獻(xiàn)[13]給出了FOX算法的差分-碰撞攻擊,攻擊需要的數(shù)據(jù)復(fù)雜度很小,但預(yù)處理復(fù)雜度較高。文獻(xiàn)[14]給出了FOX算法的差錯(cuò)故障分析結(jié)果。
本文首先給出了FOX64算法大量4輪零相關(guān)線性逼近,然后利用零相關(guān)線性逼近區(qū)分器與積分區(qū)分器的關(guān)系,首次得到了FOX64算法4輪積分區(qū)分器。最后,利用積分分析方法對(duì) 5,6,7,8輪 FOX64進(jìn)行了攻擊。
2 基礎(chǔ)知識(shí)
本節(jié)首先簡(jiǎn)單介紹 FOX算法及其圈函數(shù)線性逼近的一般規(guī)律,然后介紹零相關(guān)線性分析。
2.1 FOX分組密碼算法[7]簡(jiǎn)述
FOX算法使用的圈函數(shù)是嵌套 SPS結(jié)構(gòu)的Lai-Massey模型。限于篇幅,只對(duì)FOX64進(jìn)行詳細(xì)介紹,F(xiàn)OX128可看作兩個(gè) FOX64的并置。FOX64/k中的k是密鑰長(zhǎng)度。
輪函數(shù) f : {0,1}32×{0,1}64→{0,1}32由字節(jié)代替變換sigma4、線性置換mu4和密鑰異或加構(gòu)成,其使用的子密鑰K = k0k1是 64 bit,表達(dá)式為f( x, K ) = sigma4(mu4(sigma4(x ⊕ k0) ) ⊕ k1)⊕ k0。其中sigma4: {0,1}32→{0,1}32由4個(gè)相同的8進(jìn)8出的 s盒并置而成,擴(kuò)散層 mu4: [GF(256)]4→[GF(256)]4使用一個(gè)分支數(shù)為5的MDS矩陣,其定義為
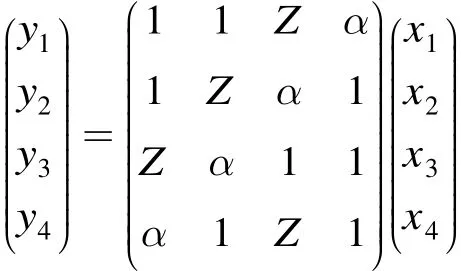
Z = α-1⊕ 1 ,α 是不可約多項(xiàng)式 m ( x ) = x8⊕ x7⊕x6⊕ x5⊕ x4⊕ x3⊕ 1 的一個(gè)根。
FOX64算法圈函數(shù)迭代16次,64 bit明文P經(jīng)加密后得到的64 bit密文為
C=Imid64( Imor64 ( …(Imor64 ( P , K1),… ,K2),Kr)其中圈函數(shù) I mor64(xl||xr) =or(xl⊕f32(xl⊕xr,k ))||(yr⊕f32(xl⊕xr,k )),K1, K2,…,Kr是各圈使用的64 bit子密鑰,or(x, y ) = ( y, x ⊕ y ) 是圈函數(shù)使用的線性正形置換,最后一輪圈函數(shù)Imid64無正形置換。
設(shè) FOX算法中使用的正形置換or對(duì)應(yīng)矩陣為M。給出FOX64算法圈函數(shù)線性逼近對(duì)應(yīng)的一般規(guī)律。
引理1 FOX64算法圈函數(shù)Qk的線性逼近(α, β)→ (A, B)的相關(guān)系數(shù)為非零ρ的充分必要條件是α ⊕ β ⊕ B⊕ M A=0。此時(shí),F(xiàn)函數(shù)對(duì)應(yīng)的線性逼近為 β ⊕ B → α ⊕ β 且滿足相關(guān)系數(shù)也是 ρ 。
證明 設(shè) ( x1,x2)為 Qk的輸入,令 x =x1,y = x1⊕x2,將x, y看作列向量,則有
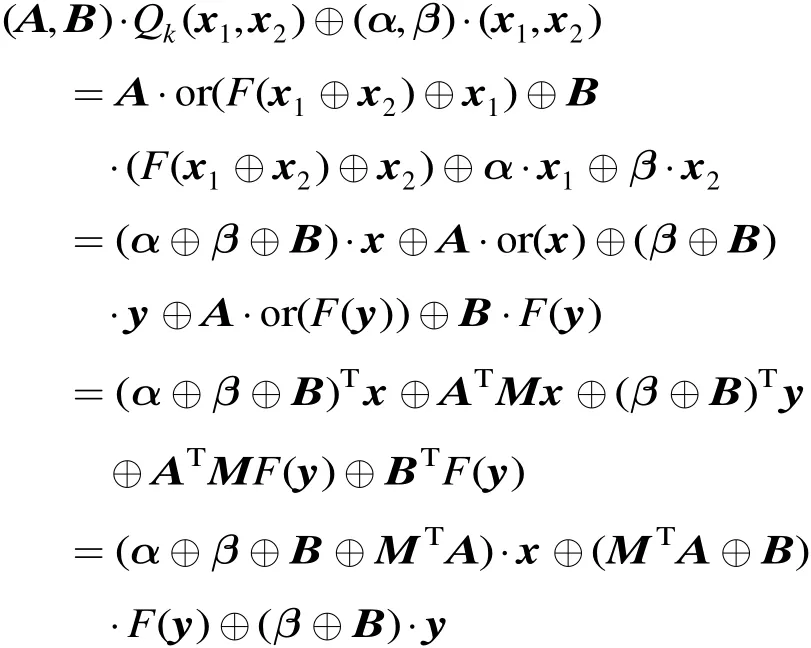
本 文 記 Δ=α ⊕ β ⊕ B⊕MTA , Γ( y ) = (MTA⊕B ) ? F (y ) ⊕ (β ⊕ B)?y 。則有
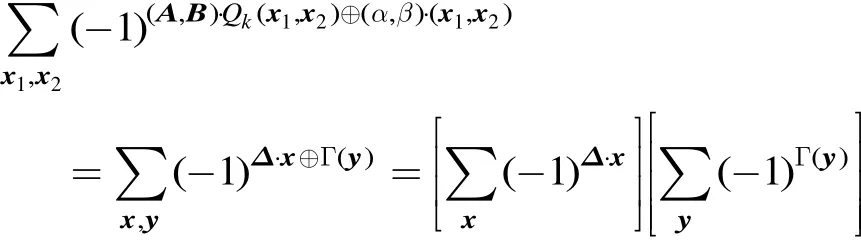
F F特別地,由于正形置換or滿足 MT=M ,可得α ⊕ β ⊕ B⊕ M A=0。充分條件顯然。 證畢
此外,F(xiàn)OX算法使用的正形置換or(x, y)=(y, x ⊕y)及逆置換io(x, y ) = ( x ⊕ y , x)具有的性質(zhì)為:
性質(zhì) 1[7](1) or2(x, y ) = i o(x, y), io2(x, y)=or(x, y ) ; (2)io(x, y ) ⊕ o r(x, y ) ⊕ (x, y ) = (0,0); (3)or(x, y ) = ( x, y)當(dāng)且僅當(dāng)(x, y) = ( 0,0); (4) o r3(x, y)= ( x, y)。
2.2 零相關(guān)線性逼近[15]
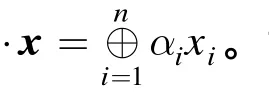
定義 1[2]給定函數(shù) F = fr-1°…° f0的一個(gè)線性堆 α → β ,稱 Γ = ( α0, α1, … ,αr) 為F函數(shù)的一個(gè)起點(diǎn)為α=α0,終點(diǎn)為β=αr的組合傳遞鏈。設(shè)線性堆 α → β 的相關(guān)系數(shù)為 CF(α, β) , fi的線性特征(αi-1,αi) 的 相 關(guān) 系 數(shù) 為 Cfi( αi-1,αi), 則 有CF(α, β) = Cf1(α0, α1) Cf2(α1, α2) … Cfr(αr-1,αr)。
定義 2[2]給定函數(shù) F =° f °…° f,設(shè) r-20Γ = ( α0, α1, … ,αr) 為F函數(shù)的一條組合傳遞鏈,如果圈函數(shù) fi的線性逼近 αi→ αi+1的相關(guān)系數(shù)Cfi(αi, αi+1) = 0,則稱線性選擇模式對(duì) (αi, αi+1)是不相容的。
由此,文獻(xiàn)[3]給出了零相關(guān)線性逼近存在的充分條件為:
引理 2[3]給定函數(shù) F =° f °…° f,設(shè) r -20α → β為F函數(shù)的一個(gè)線性堆對(duì)應(yīng),如果該線性堆的任意一條組合傳遞鏈 Γ = ( α, α1, L,αr-2,β)至少存在一對(duì)不相容的選擇模式對(duì),則 CF(α, β) = 0。
此外,本文給出如下幾個(gè)引理和定義:
引理 3[3]對(duì)于置換P,其相關(guān)系數(shù)非零的充分條件是輸入、輸出選擇模式都為零或者都不為零。
定義3[2]如果 X = (x0, x1, … , xn-1) ∈ ()n,則稱wt(X) = # {0 ≤ i ≤ n - 1 : xi≠0}為X的重量。
定義 4[2]設(shè)線性變換 L ( x ) =Ax,則線性分支數(shù)定義為 Bl= m in{wt(ATΓ y ) + w t(Γ y ) : Γ y ≠0},其中 AT表示矩陣A的轉(zhuǎn)置。
2.3 零相關(guān)-積分分析
文獻(xiàn)[5]研究了零相關(guān)線性區(qū)分器與積分區(qū)分器的關(guān)系,并將由零相關(guān)線性區(qū)分器得到積分區(qū)分器,然后利用積分區(qū)分器攻擊分組密碼算法的分析方法稱為零相關(guān)-積分分析。本文進(jìn)一步研究?jī)深悈^(qū)分器的關(guān)系:
引理4[16]設(shè),ξ η均是二元隨機(jī)變量,且ξ服從等概分布,則ξη⊕服從等概分布的充分必要條件是ξ與η獨(dú)立。
引理 5[16]設(shè) ξ1, ξ2,… ,ξm和 η1, η2,…,ηn都是二元隨機(jī)變量,則 (ξ1, ξ2,… ,ξm)與(η1, η2,… ,ηn)獨(dú)立等價(jià)于對(duì)所有二元非零向量 (a1, a2,… ,am)和(b1, b2,…,bm),a1ξ1⊕ a2ξ2⊕ … ⊕amξm與b1η1⊕b2η2⊕ … ⊕bnηn均獨(dú)立。
證明 由于任意非零的 a , b, c, d∈F28,有α?x⊕β ? f (x)的 相 關(guān) 系 數(shù) 為 零 , 即 [a ? (x1⊕ x3) ⊕ b ? (x2⊕x4)]⊕ [c ? (y1⊕ y3) ⊕ d ? (y2⊕ y4)]為平衡函數(shù),所以(x1⊕ x3, x2⊕ x4)是平衡函數(shù),故由引理4知上式等價(jià) 于 a ? (x1⊕ x3) ⊕ b ? (x2⊕ x4)與 c ? (y1⊕ y3) ⊕ d ? (y2⊕y4)獨(dú)立,再由引理 5可知 ( x1⊕ x3,x2⊕x4)與(y1⊕ y3, y2⊕ y4)獨(dú)立。所以對(duì)任意給定的常值λ1, λ2,加密形如 (x1, x2, x1⊕ λ1, x2⊕ λ2, x3x4x5x6)的所有可能輸入, (y1⊕ y3, y2⊕ y4)每個(gè)可能值出現(xiàn)的次數(shù)是相同的。 證畢
其中 α =(a bab,0000)和 β =(c dcd,0000)最后位置都為0,只是為了形式簡(jiǎn)單而為之。
3 低輪FOX64算法的零相關(guān)線性分析
3.1 4輪FOX算法零相關(guān)線性區(qū)分器
定理 1 如 果 α ∈{0,1}32{0}且wt(α)+wt(α ⊕ β ) ≤ 4,則(io(α) , io(α) ) → (io(β ) ,io(β))是4輪FOX64(最后一輪無正形置換)的零相關(guān)線性區(qū)分器。
證明 如圖1所示,當(dāng)輸入選擇模式為(io(α),io(α))時(shí),設(shè)第1輪圈函數(shù)的輸出選擇模式為(A ,B ),由引理1可知io(α) ⊕ i o(α) ⊕ B⊕ M A=0,即A = M-1B,且 f1的輸入選擇模式和輸出選擇模式分別為io(α)⊕B和io(α) ⊕ i o(α) =0。再由引理3可知,f1輸出選擇模式為0,相關(guān)系數(shù)非零的輸入選擇模式必為0,即io(α) ⊕ B =0,得 B = io(α),由此可得 A = or(α),即第 2圈的輸入選擇模式為(or(α) , io(α) ) 。對(duì)第2輪圈函數(shù)使用引理1,得 f2的輸出選擇模式為or(α) ⊕io(α) =α。假設(shè) f2的輸入選擇模式為b,由引理1可得第2圈的輸出選擇模式為(α ⊕io(b ) ,io(α) ⊕ b)。
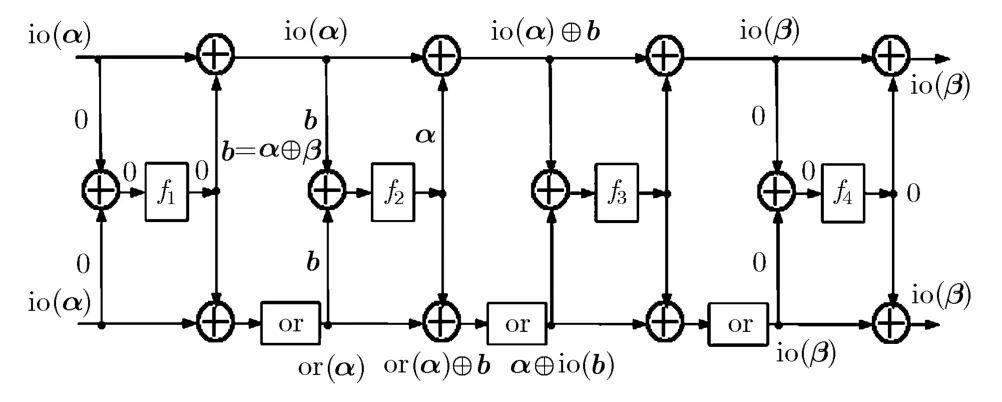
圖 1 4輪FOX64的零相關(guān)線性區(qū)分器
當(dāng)?shù)?圈輸出選擇模式為(io(β) ,io(β) )時(shí),可知第4圈的輸入選擇模式為(io(β ) ,io(β ) )。此時(shí),對(duì)第3輪圈函數(shù)使用引理 1有 α ⊕ i o(b ) ⊕ i o(α)⊕b⊕io(β) ⊕ β = 0, 可 得or(b ) = o r(α ⊕ β), 即 b =α ⊕ β。因此, f2的輸入選擇模式和輸出選擇模式分別為α⊕β和α。故當(dāng)wt(α) + w t(α ⊕ β ) ≤4時(shí),α ⊕ β → α 是 不 相 容 的 。 所 以(io(α),io(α))→(io(β) ,io(β ) )是4輪FOX64的零相關(guān)線性區(qū)分器。證畢
推論1 對(duì)于任意非零字節(jié) a, b, c, d, 4輪FOX64算法具有3類零相關(guān)線性區(qū)分器:
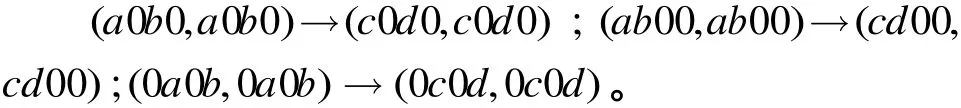
證明 當(dāng)4輪FOX64算法的輸入選擇模式和輸出選擇模式分別為(a0 b 0,a0 b 0 )和(c0 d 0 ,c0 d 0 )時(shí),有wt(or(a0 b 0 )) + wt(or(a0 b 0 ) ⊕ or(c0 d 0)) = 2 + 2 = 4 成立,由定理1可知(a0 b 0 ,a0 b 0 ) → (c0 d 0 ,c0 d 0)為4輪FOX64算法的零相關(guān)線性逼近。同理可證另外兩種情況。 證畢
3.2 低輪FOX64的零相關(guān)-積分分析
本節(jié)將利用上節(jié)給出的4輪FOX的零相關(guān)線性區(qū)分器構(gòu)造4輪積分區(qū)分器,同時(shí)對(duì)低輪的FOX64算法進(jìn)行零相關(guān)-積分分析。為此,首先給出引理7。
引理 7 對(duì)于 4輪 FOX64(最后一輪無正形置換),設(shè)4輪FOX64的輸出為 (w1w2w3w4, w5w6w7w8),則
(1)加密 248個(gè)所有可能明文 ( p1p2p3p4, p1p5p3p6),w1⊕w5, w3⊕w7的28個(gè)可能值各出現(xiàn) 240次;
(2)加密 248個(gè)所有可能明文 (p1p2p3p4, p5p2p6p4),w2⊕w6, w4⊕w8的28個(gè)可能值各出現(xiàn) 240次;
(3)加密 248個(gè)所有可能明文 (p1p2p3p4, p1p2p5p6),w1⊕w5, w2⊕w6的28個(gè)可能值各出現(xiàn) 240次。
證明 (1)由推論 1可知(a0 b 0,a0 b 0) → (c0 d 0,c0 d 0 )為4輪FOX64算法的零相關(guān)線性逼近,然后取引理6中的λ=0,即可得此結(jié)論。同理可得到引理7(2)和引理7(3)。 證畢
下面證明中,令明文結(jié)構(gòu) P1={(p1p2p3p4,p1p5p3p6) | pi∈F28,i =1,2,… ,6},P2={(p1p2p3p4,p5p2p6p4) | pi∈F28,i =1,2,… ,6},P3={(p1p2p3p4,p1p2p5p6) | pi∈F28,i =1,2,… ,6}。
設(shè)第 5輪 64 bit子密鑰為 R K5=||, 5輪FOX64(最后一輪無or變換)的輸出為 (CL, CR) = (u1u2u3u4, u5u6u7u8)。其中,對(duì)于第5輪的Imid64變換,輸入塊的異或和等于輸出塊的異或和。所以第5輪F函數(shù)的輸入為CL⊕CR。
引理8 對(duì)于5輪FOX64(最后一輪無or變換),第4輪的輸出 (w1w2w3w4, w5w6w7w8)(未經(jīng)過or變換)與密文 (CL, CR) = (u1u2u3u4, u5u6u7u8)及 64 bit密鑰RK5=的關(guān)系為:
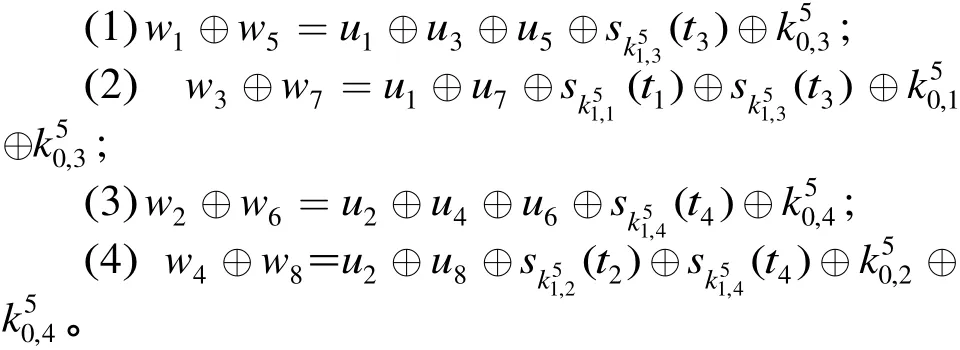
其 中(t1t2t3t4) =mu4(sigma4(CL⊕ CR⊕)),( tj)=s[mu4(sigma4(ΔC ⊕⊕]。
證明 由 于 f5( CL⊕CR, RK5) = sigma4(mu4?(sigma4(CL⊕ CR⊕⊕⊕,所以已知及 CL⊕CR的值,即可求得(t1t2t3t4) = mu4(sigma4?(CL⊕ CR⊕))的值。此時(shí),有
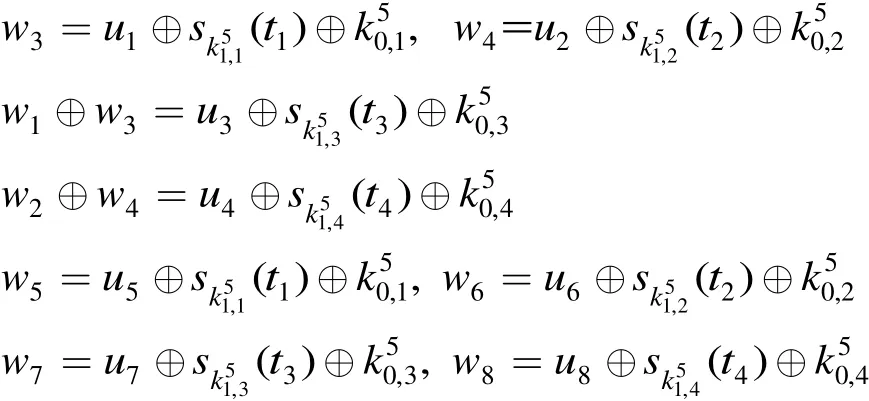
所 以 w1⊕ w5=w1⊕w3⊕w3⊕ w5=u1⊕u3⊕u5⊕(t)⊕,同理可證其它等式。 證畢3
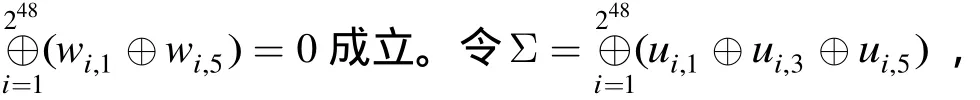
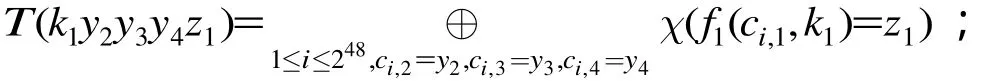
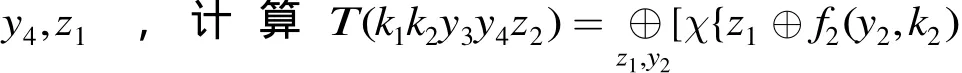
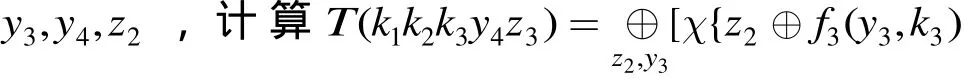
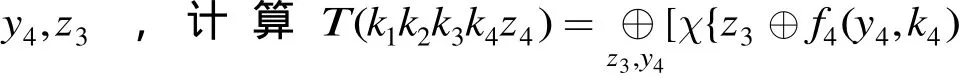
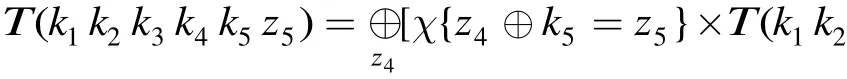
步驟1的時(shí)間復(fù)雜度為 248× 28= 256,空間復(fù)雜度為232。步驟2到步驟5的時(shí)間復(fù)雜度均為 248,空間復(fù)雜度分別為224, 216, 28, 1。故算法1的時(shí)間復(fù)雜度約為 256,空間復(fù)雜度為232。

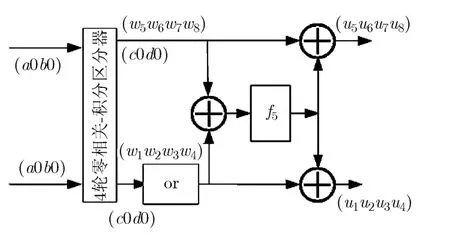
圖 2 5輪FOX64的零相關(guān)-積分分析
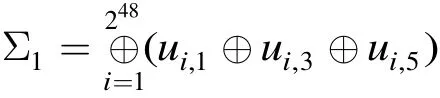

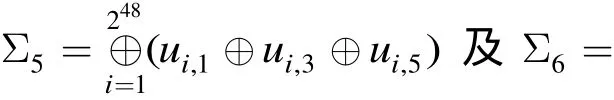
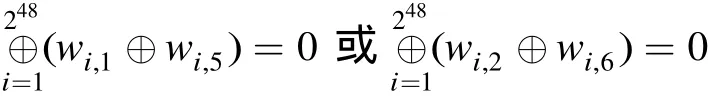
同理,利用引理 7(1)、引理 7(3),通過統(tǒng)計(jì)w3⊕w7和w4⊕w8的28個(gè)可能值是否出現(xiàn) 240次,可以分別恢復(fù)及,時(shí)間復(fù)雜度都為 256次查表。故恢復(fù) R K5的數(shù)據(jù)復(fù)雜度為 250個(gè)選擇明文,時(shí)間復(fù)雜度為 8 × 256= 259次查表運(yùn)算。由于FOX64算法圈函數(shù)的實(shí)現(xiàn)大約需要 24次查表運(yùn)算。故該攻擊的時(shí) 間復(fù) 雜 度 約 為 259× 2-4× 1 /5 ≈ 252.7次5輪FOX64加密。獲得第5輪圈子密鑰 R K5后,我們可以利用文獻(xiàn)[9]給出的4輪FOX64的積分攻擊恢復(fù)前4輪子密鑰,其復(fù)雜度約為 245.4次4輪FOX64加密。此外,對(duì)于6輪FOX64的攻擊,我們可以通過窮舉第6輪全部64 bit子密鑰來實(shí)現(xiàn),其時(shí)間復(fù)雜度約為 2116.7次6輪FOX64加密。同理可知,對(duì)7輪和8輪FOX64攻擊的時(shí)間復(fù)雜度約為 2180.7和2244.7次加密。
4 結(jié)束語
本文分析了 FOX64算法抗零相關(guān)線性分析的能力,并利用零相關(guān)線性分析與積分分析相結(jié)合的方法分析了FOX64算法的安全性,結(jié)果表明零相關(guān)-積分分析對(duì)低輪FOX64算法是一類有效的攻擊。攻擊的數(shù)據(jù)復(fù)雜度為 250個(gè)選擇明文,攻擊 5輪FOX64/64的時(shí)間復(fù)雜度為 252.7次加密,6輪FOX64/128的時(shí)間復(fù)雜度為 2116.7次加密,7輪FOX64/192的時(shí)間復(fù)雜度為 2180.7次加密,8輪FOX64/256的時(shí)間復(fù)雜度為2244.7次加密。鑒于本文關(guān)于低輪FOX64的零相關(guān)-積分分析結(jié)果,要求設(shè)計(jì)者在設(shè)計(jì)分組密碼算法時(shí),必須評(píng)估其抵抗零相關(guān)線性分析的能力。
[1] Biham E and Shamir A. Differential cryptanalysis of DES-like cryptosystems[C]. Proceedings of the CRYPTO 1990, Santa Barbara, CA, USA, 1990, 537: 2-21.
[2] Matsui M. Linear cryptanalysis method for DES cipher[C].Proceedings of the EUROCRYPT 1993, Lofthus, Norway,1993, 765: 386-397.
[3] Bogdanov A and Rijmen V. Linear hulls with correlation zero and linear cryptanalysis of block ciphers[J]. Designs, Codes and Cryptography, 2014, 70(3): 369-383.
[4] Bogdanov A and Wang M. Zero correlation linear cryptanalysis with reduced data complexity[C]. Proceedings of the Fast Software Encryption 2012, Washington DC, USA,2012, 7549: 29-48.
[5] Bogdanov A, Leander G, Nyberg K, et al.. Integral and multidimensional linear distinguishers with correlation zero[C]. Proceedings of the ASIACRYPT 2012, Beijing,China, 2012, 7658: 244-261.
[6] Hadi S. Zero correlation linear cryptanalysis of reduced-round LBlock[J]. Designs, Codes and Cryptography,2014, To be published.
[7] Junod P and Vaudenay S. FOX: a new family of block ciphers[C]. Proceedings of the Selected Areas in Cryptography-SAC 2004, Ottawa, Canada, 2004, 2595:131-146.
[8] Vaudenay S. On the Lai-Massey scheme[C]. Proceedings of the ASIACRYPT 1999, Singapore, 1999, 1716: 8-19.
[9] Aaram Y and Je H. On Lai-Massey and quasi-Feistel ciphers[J]. Design, Codes and Cryptography, 2011, 58(1):45-72.
[10] Wu Wen-ling, Zhang Wen-tao, and Feng Deng-guo. Integral cryptanalysis of reduced FOX block cipher[C]. Proceedings of the Information Security and Cryptology-ICISC 2005, Beijing,China, 2005, 3935: 229-241.
[11] Wu Zhong-ming, Lai Xue-jia, Zhu Bo, et al.. Impossible differential cryptanalysis of FOX[C]. Proceedings of the first International Conference on Information Security: Beijing,China, 2010, 6163: 236-249.
[12] 魏悅川, 孫兵, 李超. FOX密碼的不可能差分攻擊[J]. 通信學(xué)報(bào), 2010, 31(9): 24-29.Wei Yue-chuan, Sun Bing, and Li Chao. Impossible differential attack on FOX[J]. Journal on Communications,2010, 31(9): 24-29.
[13] Chen jie, Hu Yu-pu, Zhang Yue-yu, et al.. Differential collision attack on reduced FOX block cipher[J]. China Communications, 2012, 9(7): 71-76.
[14] Li Rui-lin, You Jian-xiong, Sun Bing, et al.. Fault analysis study of the block cipher FOX64[J]. Multimedia Tools and Applications, 2013, 63(3): 691-708.
[15] Blondeau C and Nyberg K. New links between differential and linear cryptanalysis[C]. Proceedings of the EUROCRYPT 2013, Athens, Greece, 2013, 788: 388-404.
[16] 金晨輝. 有限域和剩余類環(huán)上非奇異反饋多項(xiàng)式的譜刻劃[J].通信學(xué)報(bào), 2000, 21(1): 74-77.Jin Chen-hui. Spectra characterizations of nonsingular feedback polynomials over finite fields and residue class rings[J]. Journal of China Institute of Communications, 2000,21(1): 74-77.
[17] Ferguson N, Kelsey J, Lucks S, et al.. Improved cryptanalysis of Rijndael[C]. Proceedings of the Fast Software Encryption 2000, New York, USA, 1978: 213-230.

