基于模態測試及有限元法的葉片失諧參數識別

張 亮， 李 欣，袁惠群

（1.遼寧工業大學機械工程與自動化學院，遼寧 錦州 121001；2.東北大學機械工程與自動化學院，遼寧 沈陽 110819）

0 引 言

理論上，葉片輪盤系統為周期對稱結構，但由于制造誤差、材質不均、使用磨損或人為抑制顫振等因素，葉片間會存在微小的差別，即為失諧[1-4]。失諧葉盤系統的耦合振動和振動局部化對發動機的結構完整性和工作可靠性有較大影響，因此，這方面的研究日益受到重視。

研究葉盤系統失諧振動的方法主要有集中參數法[1-3]和有限元法[4-5]，目前應用較多的是有限元法，而有限元模型輸入失諧參數的準確程度對分析結果起著舉足輕重的作用。一些學者采用隨機失諧參數來模擬葉片失諧[1，3，5]，但隨機失諧不能準確反映葉片的實際失諧情況。要預測真實失諧葉盤系統振動及動力學特性，首先要選擇一個較為合理的參數，其次是對該失諧參數進行準確識別。近年來，一些學者提出了幾種失諧識別方法[6-7]，但存在一定缺陷，參數沒有明確的物理意義，不能使實際葉片物理性質的變化直接與有限元模型矩陣相聯系。因此，葉片失諧參數的合理選擇與準確識別極大地影響著失諧葉盤系統振動及動力學特性分析的準確性。綜上，本文提出一種葉片模態測試與有限元法相結合的葉片失諧參數識別方法，并以某壓氣機一級葉片為例，識別了各葉片的失諧參數。

1 葉片失諧參數選擇

目前主要的失諧模擬類型有固有頻率[7]、阻尼[8]和振型等，但都存在片面性。失諧引起的葉片結構參數與諧調時微小差別，既不能準確獲得，也沒有必要準確獲得，而有效描述和模擬失諧，達到準確度要求是最終目標[9]。

本文假設輪盤諧調，只考慮葉片材料參數變化，通過對N個葉片的彈性模量引入不同的擾動系數Pj來模擬葉片彈性模量的改變，即模擬葉片失諧：

式中：E0——葉片材料彈性模量（諧調葉片）；

Ej——第j個葉片的失諧彈性模量；

Pj——第j個葉片失諧彈性模量的擾動系數。

Pj雖不能完全描述葉片其他形式的失諧，但包含了其他形式失諧的彈性等效值，因而可定量比較葉盤結構各扇區的葉片失諧；Pj具有明顯的物理意義，可以與有限元模型矩陣相聯系，在采用組件模態綜合（CMS）分析時，式（1）表示把每個葉片的整體剛度作為子矩陣，每個葉片引入了一個失諧彈性模量擾動系數[10-11]。

2 葉片失諧參數識別

對于如何識別擾動參數Pj，本文提出了一種葉片模態測試與有限元法相結合的方法。葉片失諧參數識別具體方案如下：

1）搭建葉片模態測試裝置，采用共振法測試各葉片一階彎曲靜頻。即當葉片在激振力作用下，且當該力的頻率等于葉片自振頻率，其位置和相位適當時，葉片則由強迫振動進入共振狀態。通過測量激振力的頻率可以獲得葉片的自振頻率。圖1為葉片模態測試方案，主要由固持系統、激振系統和測試系統3部分組成。

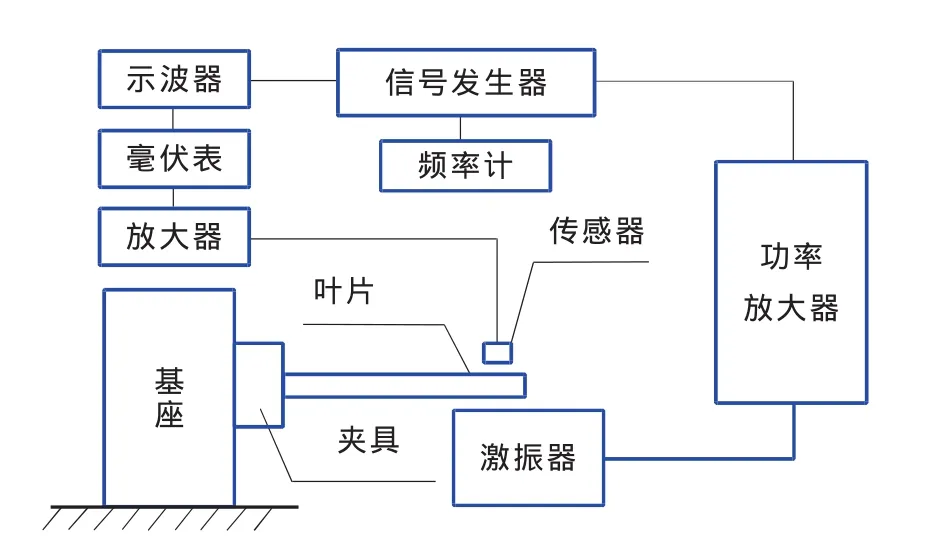
圖1 葉片靜頻測試方案

固持系統：由安裝葉片的夾具和基座組成。夾具應夾緊葉片，符合葉片的工作狀態。葉片處于發動機正常工作狀態時，受到很大的離心力作用，使葉片根部接近于完全固持狀態。

激振系統：由信號發生器、功率放大器和激振器等組成。它給被測葉片提供足夠的激振能量，以激勵葉片，產生強迫振動。激振器采用非接觸式激振器；信號發生器采用具有信號發生及掃頻輸出功能的AZ308S數據采集箱。只需設定一個掃頻范圍以及葉片測頻準確度即掃頻間隔步長，根據在此掃頻范圍內振動加速度幅值響應的最高點來確定該葉片的自振頻率。運用有限元法預估葉片一階彎曲頻率近似值，并在其±10%范圍內依次進行掃頻。

測試系統：由傳感器、放大器、毫伏表、示波器、頻率計等組成。本文采用加速度傳感器、AZ804信號調理儀、AZ308S數據采集箱及葉片測頻采集與分析軟件系統。加速度傳感器頻響范圍為1～2000Hz，靈敏度為100mV/g。AZ804信號調理儀為4通道多功能放大濾波器，具有信號放大、積分及濾波功能。放大倍率有 3檔（×1、×10、×100）。濾波截止頻率分為 9檔，分 別 為 0.005，0.01，0.02，0.05，0.1，0.5，1，5，10 kHz。AZ308S數據采集箱具有USB 2.0接口，8路并行同步采集，AD轉換準確度14bit，程控放大有5檔（×1、×2、×4、×8、×16），最高采樣頻率每通道 256 kHz，帶正弦掃頻功能。葉片測頻采集與分析軟件系統包括信號采集、數據處理（FFT頻譜計算）、虛擬示波器及分散度統計等模塊，通過葉片測頻采集與分析軟件控制數據采集器和計算機完成各葉片振動信號的采集與分析，進而獲得各葉片一階彎曲靜頻。某壓氣機葉片模態測試無量綱數據如表1所示，Fj為第j個葉片的一彎靜頻測試值；F為諧調葉片（與材料彈性模量E0相對應）一彎靜頻測試值。

表1 某壓氣機一級葉片靜頻測試數據

2）建立葉片三維實體模型及有限元網格模型，如圖2所示。根據葉片材料彈性模量參數，給定彈性模量失諧上下限，采用有限元法對單個葉片進行模態分析，邊界條件設置為葉片與輪盤交界接觸面各節點的位移全約束。

3）葉片失諧參數識別流程如圖3所示。首先，計算彈性模量上下限所對應的葉片一階彎曲固有頻率；其次，通過二分法迭代計算，將葉片模態測試獲得的一彎靜頻與葉片一彎固有頻率有限元分析結果對比，誤差＜0.01作為計算收斂標準，進而給出與葉片模態測試相對應的單個葉片失諧擾動參數Pj和失諧彈性模量Ej；最后，選擇幾個葉片進行上述分析，獲得與葉片模態測試相對應的葉片失諧彈性模量，通過擬合計算獲得與葉片模態測試相對應的各葉片失諧彈性模量。

3 葉片失諧參數識別結果

通過Matlab軟件調用ANSYS軟件執行如圖3所示葉片失諧參數識別流程，根據文獻[12]，輸入諧調葉片材料參數為：密度ρ0=4380kg/m3，泊松比μ0=0.3，彈性模量E0=1.135×105MPa，δ值由試算確定，得到葉片失諧彈性模量分布。葉片彈性模量與一階彎曲無量綱固有頻率測試值的對應關系如圖4所示。

圖2 葉片三維實體模型及有限元模型

圖3 葉片失諧參數識別流程圖

從圖中可以看出，失諧彈性模量與葉片一階無量綱固有頻率測試值之間為近似線性關系，因此，通過線性擬合得到失諧彈性模量隨葉片一階彎曲無量綱固有頻率測試值變化的表達式：

式中：Ej——失諧彈性模量，MPa；

Fj——第j個葉片的一階彎曲靜頻測試值；

F——諧調葉片一彎靜頻測試值。

圖4 失諧彈性模量與一階無量綱固有頻率測試值關系曲線

對同一輪盤上，同種材料其他葉片的失諧擾動參數和失諧彈性模量識別時，不必按如圖3所示的流程識別，而直接將失諧葉片一階彎曲無量綱靜頻測試值代入到式（2）中，即得到與失諧葉片一階彎曲無量綱靜頻測試值對應的失諧彈性模量，如表2所示，從而節省了大量時間。

表2 失諧彈性模量識別結果

4 結束語

本文通過引入不同的葉片彈性模量擾動參數模擬葉片失諧，提出了一種基于葉片模態測試與有限元分析相結合的葉片失諧參數識別方法。并以某壓氣機一級葉片為例，識別了葉片的失諧參數。結果表明：該方法識別速度較快且準確度高，可廣泛應用于航空發動機、燃氣輪機、汽輪機等透平機械葉片的失諧參數識別。

[1] 張亮，袁惠群，韓清凱，等.基于微動滑移摩擦模型的失諧葉盤系統振動分析[J].振動工程學報，2012，25（3）：289-293.

[2] 姚建堯，王建軍，李其漢.失諧葉盤結構魯棒性能分析[J].航空動力學報，2010，25（7）：1634-1639.

[3] 袁惠群，張亮，韓清凱，等.基于蟻群算法的航空發動機失諧葉片減振排布優化分析[J].振動與沖擊，2012，31（11）：169-172.

[4] 王建軍，于長波，李其漢.錯頻葉盤結構振動模態局部化特性分析[J].航空動力學報，2009，24（4）：788-792.

[5] 秦飛，陳立明.失調葉片-輪盤系統耦合振動分析[J].北京工業大學學報，2007，33（2）：126-128.

[6] Kim N E，Griffin J H.System identification in high modal density regions of bladed disks[C]∥The 8th National Turbine Engine High Cycle Fatique Conference Monterey USA，2003.

[7] Feiner D M，Griffin J H.Mistuning identification of bladed disks using a fundamental mistuning model-Part I：Theory[J].Journal of Turbomachinery，2004，126（1）：150-158.

[8] Bladh R，Castanier M P，Pierre C.Reduced order modeling and vibration analysis of mistuned bladed disk assemblies with shrouds[J].ASME J Eng Gas Turbines Power，1999（121）：515-522.

[9] Mignolet M P，Rivas-Guerra A J，Delor J P.Identification of mistuning characteristics of bladed disks from free response data-Part I[J].Journal of Engineering for Gas Turbines and Power，1999，123（2）：395-403.

[10]王帥，王建軍，李其漢.一種基于模態縮減技術的整體葉盤結構失諧設別方法[J].航空動力學報，2009，24（3）：662-669.

[11]張亮.航空發動機葉片輪盤系統振動特性及多場耦合力學特性研究[D].沈陽：東北大學，2013.

[12]中國航空材料手冊[M].北京：中國標準出版社，2002：72-91.