巖石可鉆性及巖石破碎機理探討

吳其干

（廣東省有色金屬地質局九三一隊，廣東汕頭515041）

巖石可鉆性及巖石破碎機理探討

吳其干*

（廣東省有色金屬地質局九三一隊，廣東汕頭515041）

目前的巖石可鉆性分級與實際的鉆進時效有出入，相應的巖石在壓頭下破碎機理的觀點也很難解析破碎坑的頂角和大小問題，通過進一步的探討和計算，做出了巖石在壓頭下破碎機理的推論，并對巖石可鉆性的劃分提出了建議。

可鉆性；破碎機理；探討

通常在選用鉆頭及選擇鉆壓等鉆進參數時，主要以巖石的可鉆性等級為依據，而巖石的可鉆性等級則主要根據壓入硬度的大小進行劃分，但在實際巖芯鉆探過程中，往往會發現實際的鉆進時效與預計鉆進時效差別很大，例如壓入硬度相差不大的黑云母花崗巖（462kg/mm2）和灰白色顆粒石英砂巖（471kg/mm2）鉆進的實際時效分別為1.97m/h、0.63m/h，差別很大。可見目前巖石的可鉆性等級分類不太合理，需進一步探討。了解和掌握巖石在壓模作用下破碎機理將有助于我們更合理地劃分巖石的可鉆性等級。

目前有關巖石在壓模作用下破碎機理的觀點有多種，但都很難解析壓模所產生破碎坑的角度及大小問題，而且有關破碎坑大小試驗資料也不一致：目前被較普遍接受的破碎坑的直徑為，脆性巖石破碎坑的直徑為壓模直徑的5～8倍，塑性巖石破碎坑的直徑為壓模直徑的3～4倍。而根據前蘇聯A.T包爾德諾娃和H.H巴符洛娃的試驗結論，脆性和小塑性巖石破碎坑的直徑為壓模直徑的3～4倍，塑性巖石破碎坑的直徑則為壓模直徑的5～8倍。兩者之間相矛盾。因此有必要對巖石在壓模作用下的破碎機理進一步探討。

1 壓模下巖石破碎機理的推理

有關巖石在壓模作用下破碎機理，個人認為應遵循庫倫—莫爾原則：接觸面下方的裂紋并非是產生于最大剪應力，而是當接觸面下方某處的應力沿剪切滑移面方向的分力大于摩擦力和內聚力之和時產生。壓模下面某處的應力除了垂直方向的主應力σz外，還有水平徑向方向的應力σr等應力。設τ為沿剪切滑移面方向的應力、σ為剪切滑移面上的正應力，那么壓模下面某處沿剪切滑移面方向的應力τ及剪切滑移面上的正應力σ分別為：

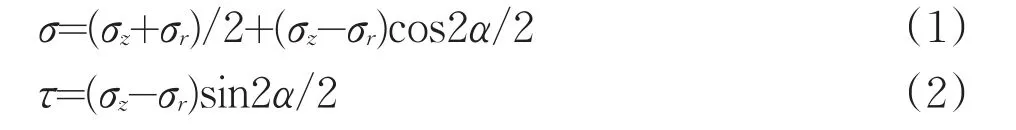
式中：α——最大主應力與剪裂面法線之間的夾角。

根據庫倫—莫爾原則，當沿剪切滑移面方向的應力τ滿足下面條件時產生剪切裂紋。

式中：σ——剪切滑移面上的正應力；

ψ——摩擦角；

C——內聚力。

壓模下面某處垂直方向的主應力σz及水平徑向方向的應力σr可通過下面公式求得：

將τ=σtanψ+C對Z求導并使其等于零，便可得到剪應力τ減去摩擦力（σtanψ）后為最大值的深度Z0：

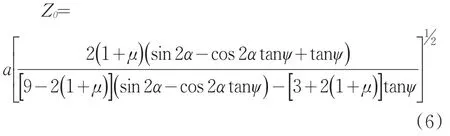
式中深度Z0是產生剪切裂紋的源點，a為壓模半徑，最大主應力與剪裂面法線之間的夾角α=π/4+ψ/2。壓頭下面巖石破碎的方式推理如下：如圖1所示，巖石在負載作用下首先產生接觸變形，然后在接觸面下方Z0處產生剪切裂紋源1；在接觸面邊緣則產生最大拉應力，形成赫茲裂紋2，然后裂紋源擴展和交匯，沿裂紋交匯線形成脫離圍巖的錐狀獨立巖體，此時獨立巖體內部及下面的圍巖已存在內傷（裂紋），極易在壓力下剪切破碎。當獨立巖體在壓力下向下擠壓時，該獨立巖體與下面圍巖的重疊部分首先被擠壓破碎并被壓密成密實體，在獨立巖體及其下面的巖石在壓頭的壓力下剪切破碎的同時，密實體通過傳遞的壓力使其下面的巖石沿剪切方向壓縮并因此對圍巖產生擠壓，當壓力增加到一定程度時，水平方向的擠壓力將圍巖（與水平面）沿剪切角方向擠壓崩離，形成錐體破碎坑。

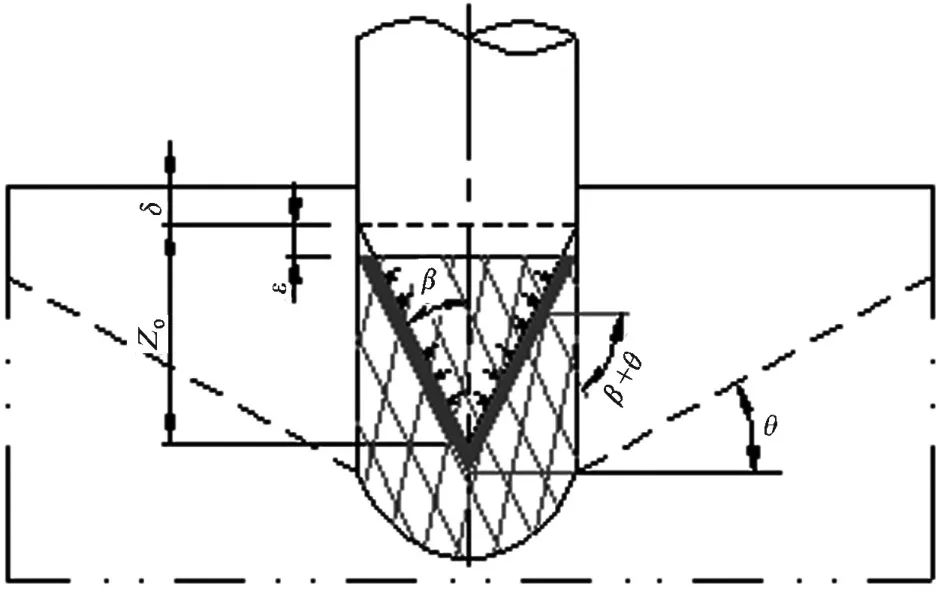
圖1 巖石在壓力作用下產生剪切破碎坑示意圖

2 破碎坑大小及壓入硬度的推算驗證

2.1 破碎坑大小的推算

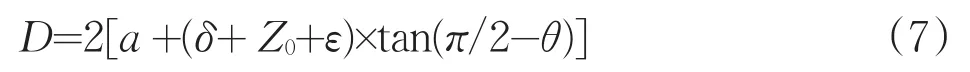
破碎坑的大小可按上述推論進行推算，其直徑為：式中θ為巖石的剪切角(θ=π/4-ψ/2)，δ為在壓頭壓力作用下產生剪切裂紋源點前的壓縮深度，ε為獨立巖體的壓深，根據巖石的變形性質，脆性巖石主要為堅硬致密以及堅硬巖石，參考工程巖體分級標準附錄C表C.0.1、常見巖石的強度及泊松比可知，其摩擦角ψ通常大于50°,泊松比μ通常小于0.25。根據(6)式和(7)式可得：在不考慮δ及ε的情況下，破碎坑的直徑D=9.2～15.7a，從而可得出脆性巖石破碎坑的直徑與壓模直徑之比為4.6～7.85倍，若考慮δ及ε，則破碎坑的直徑為壓模直徑的5～8倍；至于塑性巖石（摩擦角ψ＜50°,泊松比μ=0.2～0.35）,通過計算，在不考慮δ及ε的情況下，其破碎坑的直徑為壓模直徑的3～5倍，受δ及ε的影響，破碎坑的直徑應為壓模直徑的4～6倍，個別巖石（如片理平行于壓力方向的片巖）破碎坑的直徑大于壓模直徑的7～8倍。計算結果符合試驗結論。

2.2 壓入硬度的推算

根據上述推論，使圍巖產生剪切破碎坑的擠壓力F擠來自密實體傳遞的壓力，這些壓力將破碎巖石沿剪切角方向推動，在克服摩擦力后將剩余壓力作用在圍巖上，最終導致剩余壓力的水平分力將圍巖擠壓崩離，形成錐體破碎坑。

假設錐狀獨立巖體的錐頂角為2β（為便于計算，將其當成圓錐體。β=arctana/Z0），來自壓模的壓力為Fσ，那么密實體傳遞的壓力為Fσ/sinβ，該作用力沿剪切面的分力為Fσ×cosθ/sinβ，所克服的摩擦力為Fσ×sinθ× tanψ/sinβ，故其沿剪切面方向的剩余壓力為：

由于剪切面方向與水平面方向的角度為β+θ，因而使圍巖產生剪切破碎坑的水平擠壓力等于F剩×cos(β+ θ)，即：

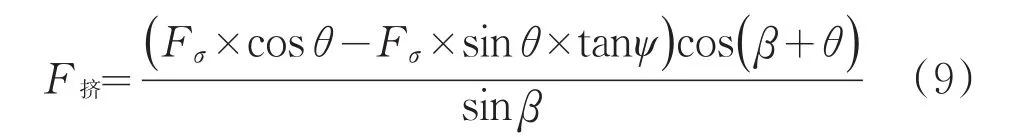
破碎巖石所需要的作用力通常按抗壓強度×受壓面積計算，即：

式中：σC——巖石的抗壓強度；

MC——受壓面積。

假設Mτ為剪切面積。則MC=Mτ×sinθ（θ為剪切角），上式可換算為：

巖石剪切破碎坑的側面積（剪切面積）為：

由(11)式和(12)式可得，使巖石產生剪切破碎坑的擠壓力F擠為：

對于壓頭的壓人深度(δ+ε)，為便于計算，脆性巖石可當成彈性體來計算。即：

式中：E——巖石的彈性模量。

塑性巖石的壓人深度(δ+ε)可按破碎坑深度與其比值為2.5～5計算：

巖石的壓入硬度可通過(9)式、(13)式、（13）或（14）以及σ壓=Fσ/πa2進行推算，例如某石英巖的單軸抗壓強度σC=350MPa；ψ=60°；E=7×104MPa所對應的μ=0.12，可推算出其σ壓=783 MPa。

3 影響壓入硬度的因素及可鉆性等級的劃分

通過計算可知，影響巖石壓入硬度的主要因素不僅有抗壓強度σC，還包括摩擦角ψ以及泊松比μ：σC越大，則壓入硬度越大；μ主要影響破碎坑的深度以及作用于圍巖的水平擠壓力(μ越大，則Z0越大，破碎坑越深；而β則越小，水平擠壓力F擠越大）；ψ不僅影響破碎坑的深度以及作用于圍巖的水平擠壓力，還影響破碎坑的頂角(ψ越大，破碎坑越深、越大，作用于圍巖的水平擠壓力F擠越大）。在抗壓強度相同的情況下，致密巖石、摩擦角較小的巖石由于產生的破碎坑小(剪切面積小)，所測得的致密巖石的壓入硬度會偏小，但由于作用于圍巖的水平擠壓力F擠小，其實際上的壓入硬度(在破碎坑大小相同的情況下)反而更大。

表1 巖石可鉆性分級表

由于壓頭壓入不同巖石產生的破碎坑的深度及大小不同，因而光用壓入硬度來表示巖石的可鉆性級別會不大準確。個人認為壓入硬度應考慮破碎坑深度及大小的因素，用壓入硬度除于破碎坑深度及半徑與壓頭半徑之比的乘積來表示，這樣所得的壓入硬度新值更能反映巖石的可鉆性，壓入硬度=700kg/mm2的巖石（可鉆性12級）主要為堅硬、致密的巖石，其摩擦角ψ通常大于55°,泊松比μ通常小于0.12，彈性模量E通常大于7×104MPa。當ψ=55°，μ=0.12，E=7×104MPa時，求得破碎坑深度與壓頭半徑之比=1.439，破碎坑半徑與壓頭半徑之比=5.564，故其壓入硬度新值=87.4kg/mm2；同樣，可求得壓入硬度=90kg/mm2的巖石（摩擦角ψ通常小于35°,泊松比μ通常大于0.35，破碎坑深度與壓人深度的比值為2.5）的壓入硬度新值為9.5kg/mm2，因而建議巖石可鉆性按表1進行分級。該分級可比較合理地反映巖石的可鉆性，例如某寒武紀石英砂巖的抗壓強度σC為68 MPa，摩擦系數為0.54（摩擦角ψ為28°）,彈性模量E為5.4×104MPa，所對應的泊松比μ為0.14。通過推算，按原可鉆性分級推算出的壓入硬度為159kg/mm2,可鉆性5級；而測試的可鉆性同為5級中粒石英砂巖（122kg/mm2）鉆進的實際時效為0.58m/h，按鉆進時效分則為11級，差別很大；而若按表1分級進行推算，其壓入硬度新值為66kg/mm2,可鉆性9～10級，與鉆進時效比較接近。

[1]修憲民，等.巖石力學性質及可鉆性分級研究[J].云南地質，2001（3）.

[2]武漢地質學院.鉆探工藝學（上冊）[M].地質出版社，1980.

[3]屠厚澤，高森.巖石破碎學[M].地質出版社，1990.

[4]張祖培，劉寶昌.碎巖工程學[M].地質出版社，2004.

[5]中華人民共和國水利部.GB50218-94工程巖體分級標準[S].

[6]顧曉魯，等.地基與基礎[M].中國建筑工業出版社，1993.

P634.1

A

1004-5716(2015)01-0070-03

2014-05-27

2014-12-08

吳其干（1965-），男（漢族），廣東梅州人，工程師，現從事探礦工程技術和相關管理工作。