基于對數變換的灰色預測模型GM (1,1)對全運會男子100m跑成績的預測研究
李 陽,陳愛華,楊莉然
基于對數變換的灰色預測模型GM (1,1)對全運會男子100m跑成績的預測研究
李 陽,陳愛華,楊莉然
1982年由鄧聚龍教授創立了灰色系統理論(Grey System)[1],該理論可以對時間序列短、統計數據少、信息不完全的系統進行建模與分析,從某種程度上彌補了統計學中的不足[2]。灰色系統指部分信息明確,部分信息不明確的系統[3],它對隨機的、有序的灰色過程進行預測,從而尋找其潛在的規律。目前,灰色系統理論在各行各業得到了廣泛應用。在體育學領域中,灰色關聯分析方法和GM(1,1)模型方法是當今體育科研領域灰色理論的兩大主干[4]。田徑項目在奧運會比賽項目中長期以來是我國的一個短板,但是在2013年全運會田徑男子100m決賽中,北京隊張培萌以10.08s奪冠,刷新了全運會紀錄,廣東的蘇炳添以10.12s獲得亞軍。張培萌在2013年莫斯科世錦賽跑出10.00s,刷新了全國男子100m跑紀錄,2013年5月在國際田聯鉆石聯賽上海站創造20.47s的男子200m全國紀錄[5]。因此,本文以此為出發點,基于灰色系統理論與方法,通過運用灰色系統模型GM(1,1),結合歷屆100m跑前三名成績,通過建立預測模型,預測下一屆全運會男子100m平均成績。為進一步完善灰色系統理論在體育中的研究做鋪墊,同時也為教練員和運動員的100m跑訓練和比賽提供理論參考。
1 研究對象與方法
1.1 研究對象
鄧聚龍先生明確指出,GM(1,1)模型的建模數據“必須等時矩,相鄰,不得有跳躍”[6]。表1顯示,第二屆和第三屆全運會相隔10年,第六屆和第七屆相隔6年,時間非等距,從第七屆開始,每隔4年舉辦一次。因此,選取1993-2013年的100m成績作為研究對象。又因影響100m跑成績的因素眾多,以前3名的平均成績來衡量我國整體優秀運動員100m跑的水平較為客觀,最終選取第七屆到第十二屆100m跑前3名的平均成績作為研究對象。
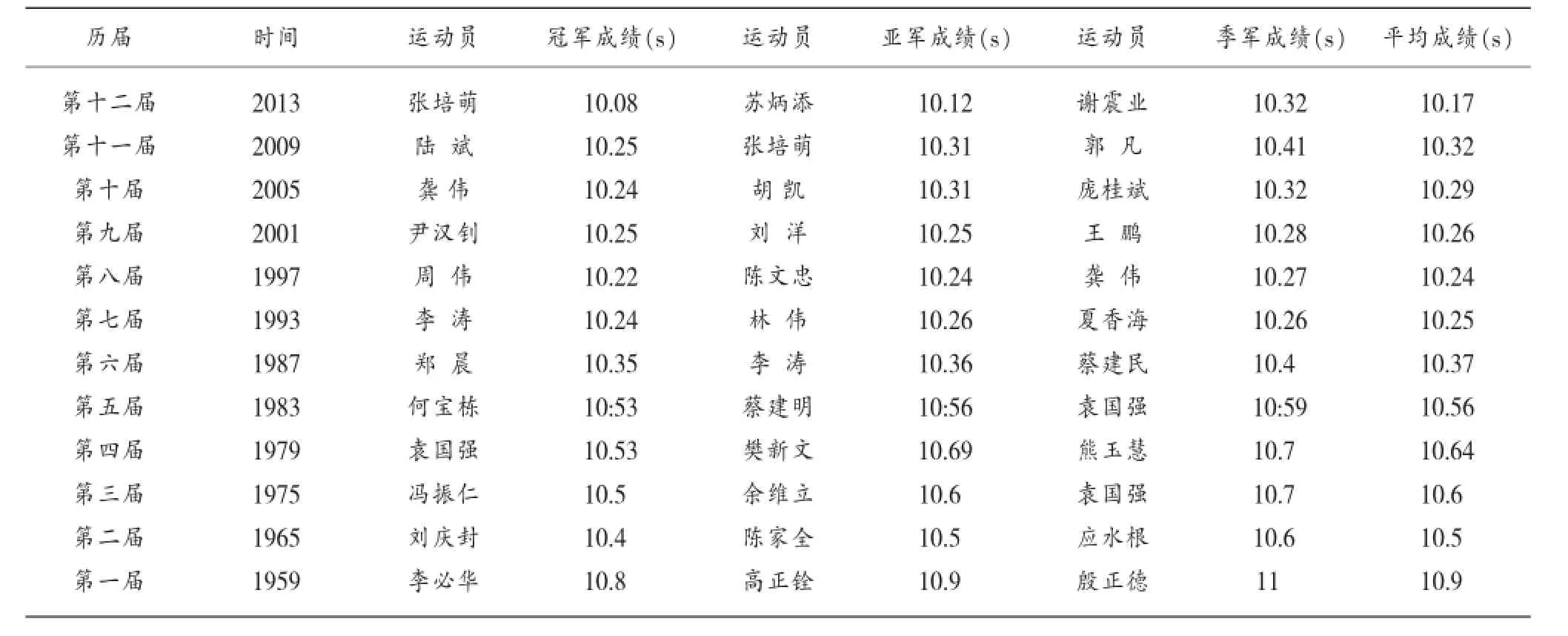
表1 歷屆全運會男子100m跑前三名成績統計表
1.2 研究方法
1.2.1 文獻資料法
查閱系統工程、灰色系統理論、系統科學、數理統計以及體育類大量相關書籍資料,檢索中國期刊網、萬方數據庫和國家體育總局官方網站。
1.2.2 灰色預測方法
1)原始數據對數變換處理。傳統的GM(1,1)模型要求原始數據為光滑序列[7],原始數據越光滑,其預測模型越精確。但是100m跑成績并不是線性的光滑數列。因此,要對數據做處理。對原始數據的處理主要有3種方法:對數變換[8]、指數變換[9]、對數函數—冪函數變換[10]、冪函數—指數函數復合變換[11]、余切函數變換[12]等。本文主要運用對數變換的方法處理原始數據,并做一次累加生成得到新的數列 x(1)={x1(1),x2(1),x3(1),x4(1),x5(1),x6(1)}。
2)確定數據矩陣:B,Yn
3)計算:(BTB)-1
4)求參數列:根據(BTB)-1BTYn求出a和u
5)確定模型:x(1)(k+1)=(x1(0)-u/a)e-ak+u/a
6)精度檢驗:殘差檢驗、關聯度檢驗、后驗差檢驗
1.2.3 數理統計法
運用軟件Mathtype6.5和計算器對相關數據進行編輯和計算。
2 結果與分析
2.1 原始數據的對數變換處理
設原始數據序列Y(0)={y(0)(1),y(0)(2),y(0)(3),y(0)(4),y(0)(5),y(0)(6)}
則對應的原始數據Y(0)={10.25,10.24,10.26,10.29,10.32.10.17}
對原始數據做對數變換:設X(0)=In(Y(0)),則對數變換后的
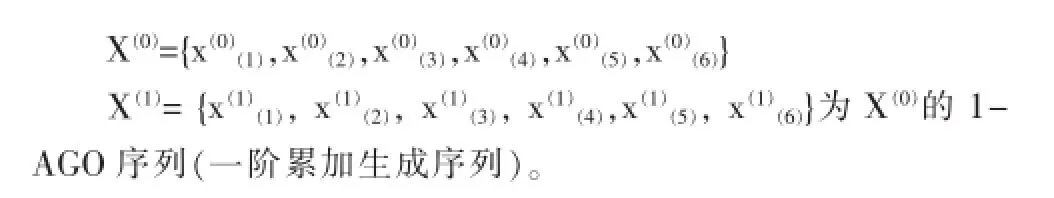
根據上式求的:
X(0)={2.3273,2.3263,2.3283,2.3312,2.3341,2.3194}
X(1)={2.3273,4.6536,6.9819,9.3131,11.6472,13.9666}
2.2 GM(1,1)建模




2.3.2 關聯度檢驗計算小誤差概率:


3 結語
2)在進行灰色預測GM(1,1)建模時首先要對原始加以處理,使原始數據序列變的平滑,如果對原始數據不加處理則誤差較大。對原始數據的處理的方法有對數變換、指數變換、對數函數—冪函數變換、冪函數—指數函數復合變換、余切函數變等,在選用不同方法時要考慮不同方法的使用條件和范圍。
3)本文只討論了前3名的平均成績,未對冠軍、亞軍和季軍各名次成績進行預測,今后可進一步進行相關研究。
[1]陳 亮.運動訓練過程組織管理的灰色系統理論與方法研究[D].曲阜:曲阜師范大學,2007.
[2]劉嘉津,孫桂云,戴美仙.灰色系統理論與方法在體育科研中的應用狀況研究[J].中國體育科技,2005,41(3):137-140.
[3]鄧聚龍.灰色控制系統[M].武漢:華中理工大學出版社,1985.
[4]劉嘉津.適用于競技體育的灰色預測方法體系研究[D].上海:華東師范大學,2007.
[5]第十二屆全運會專題.國家體育總局官網[EB/OL].http://www. sport.gov.cn/.
[6]鄧聚龍.灰色系統(社會經濟)[M].北京:國防工業出版社,1985.
[7]鄧聚龍.灰色系統理論教程[M].武漢:華中理工大學出版社,1990.
[8]陳濤捷.灰色預測模型的一種拓廣[J].系統工程,1990,8(4):50-52.
[9]何 斌.灰色預測模型拓廣方法研究[J].系統工程理論與實踐,2002,22(9):137-140.
[10]李 群.灰色預測模型的進一步拓廣[J].系統工程理論與實踐,1993,13(1):64-66.
[11]陳 潔.灰色預測模型的改進[J].遼寧師范大學學報,2005,28 (3):262-264.
[12]李翠鳳.基于函數cotx變換的灰色建模方法[J].系統工程,2005,23 (3):110-114.
[13]朱紅兵,劉建通,王 港,等.GM(1,1)模型灰色預測法及其在預測體育成績中的應用[J].首都體育學院學報,2003,15(1):120-121.
Prediction of the Result of Male 100m Run in the National Games based on the Logarithmic Transformation in Grey GM(1,1)Model
LIYang,CHEN Aihua,YANG Liran
研究目的:為預測下一屆全運會男子100m跑平均成績,通過運用灰色系統理論,建立GM(1,1)預測模型。研究方法:運用灰色系統理論預測方法、數理統計法及文獻資料調研,以第七屆到第十二屆全運會男子100m跑前三名的平均成績作為研究對象。結果與結論:通過對數變換對原始數據處理、進行GM(1,1)建模、模型檢驗(殘差檢驗、關聯度檢驗、后驗差檢驗),得到了合格的預測模型:(0)(k+1)=(1-e0.0003824)(2.3273-6194.7929)e-0.00382473k,k=6,(0)(7)=2.3233,(0)(7)=10.21(s)。即預測第十三屆全運會男子100m跑前三名的平均成績為10.21(s)。
對數變換;GM(1,1)模型;全運會;男子100m
This study usesgrey system theory to build up the predictingmodel ofGM (1,1),aim ing to predict next national sportsmeeting's 100m run average results.We uses grey system theory based on themodel of GM (1,1).The literature and mathematical statistics,regarding the 7th to 12th men's 100m run average results as the objects.Firstly,make data processing,Second ly,use the original GM (1,1),Then model test (residual test,correlation test,posterior poor inspection).Finally obtain predictionmodel:(0)(k+1)=(1-e0.0003824)(2.327 3-6 194.792 9)e-0.00382473k,k=6,(0)(7)=2.323 3,(0)(7)=10.21(s).The next national games of the men's 100m running predicting averages scores is 10.21(s).
logarithmic transformation;gm(1,1)model;the national games;male 100m
G822.1
A
1003-983X(2015)01-0047-04
2014-09-30
李 陽(1985-),男,陜西漢中人,碩士,講師,研究方向:體育教學與訓練.
蘭州大學體育教研部,甘肅蘭州730000 Department of Physical Education, Lanzhou University,Lanzhou Gansu,730000

