基于遺傳算法的UUV快速性和能源系統綜合優化分析

王蒙云，俞 強，楊松林

(江蘇科技大學 船舶與海洋工程學院，江蘇 鎮江212003)

0 引 言

UUV 是一種適合局部地區河流條件的用于水下搜索和救援行動的小型潛艇［1］。為了將搜救范圍擴展到潛水員不容易接近或根本無法到達的區域，UUV 便被大量開發并廣泛用于各種用途。根據能源系統和操作風格，UUV 大致可以分為兩類，一是ROV (纜控無人潛水器)，能源是通過電纜傳送的，通過船員使用交互式的控制系統執行任務;二是AUV (無纜自治潛水器)，能源系統獨立，可以被編寫成帶有人工干預選項的程序來完成任務［2］。

近年來，低阻力、遠程化是UUV 的發展趨勢，低阻力的UUV 擁有較好的快速性能，遠程化則要求增大UUV 的水下續航力從而擴大其活動范圍。但是，UUV 艇體阻力的減小主要通過改變艇體尺度來實現，艇體尺度的變化將影響能源艙的體積，能源艙體積的變化將影響能源艙的電量，以致影響其續航力。所以，為了提供綜合性能好的UUV 設計，從快速性和能源系統兩方面出發的綜合優化分析是必須的。該優化是一個多目標、多變量、多約束條件的復雜問題，它與諸多因素有關。由快速性定義可知，它取決于艇體阻力和推進性能，其中阻力性能與艇體主尺度、航速、以及航行環境有關;能源系統主要與能源艙的主尺度、電池的基本參數和布置方式有關。

當前，國內外的諸多高校及科研機構都在進行多學科、多目標綜合優化設計方面的研究工作。該項技術的研究主要集中于飛行器設計領域，在船舶與海洋工程領域的應用還未得到廣泛推廣［3］。在實際工程中，海洋結構物設計的優化問題往往是按照順序方式處理的，并未充分考慮各個學科之間的相互聯系，所以傳統的海洋結構物優化設計工作得到的往往是局部最優解，并非全局最優解。因此，綜合優化設計在船舶與海洋工程領域，尤其是主導未來海戰的UUV 研發方面具有十分廣闊的空間。近年來，國內針對UUV 的優化研究已取得一定成果，在低阻、降噪、艇型、耐壓殼等單性能、單目標方面進行了研究，但是考慮總體性能和能源系統的綜合優化還未進行深入分析，有待進一步研究［4-5］。

本文將建立包含快速性和能源系統的UUV 綜合優化數學模型，并基于遺傳算法構造合理高效的優化方法對該問題進行優化計算分析。

1 數學模型

從減小艇體阻力、提高推進效率方面出發，構造快速性評判指標;從能源艙的體積、重量、價格方面出發，構造能源系統評判指標。將以上2 種指標通過冪指數積的方式構造成UUV 快速性和能源系統綜合優化目標函數，而將浮性、穩性、續航力等其他性能及設計變量的限制作為約束條件［6］。

1.1 設計變量

影響AUV 快速性和能源系統的因素很多，一般影響快速性的因素，從阻力方面看，艇體的總阻力取決于排水量、航速、方形系數、主尺度、艇體型線等諸多因素;從推進方面看，對于螺旋槳推進方式、螺旋槳的效率與負荷系數直接相關，這涉及到螺旋槳的收到功率、轉速、直徑和航速等［7］。一般影響能源系統的因素有能源艙的體積、電池數量、設計航速航行時間等。綜合參考以上因素，本文選取一型水下無人艇為研究對象，采用常規單螺旋槳推進，共選取19 個設計變量(見表1)。

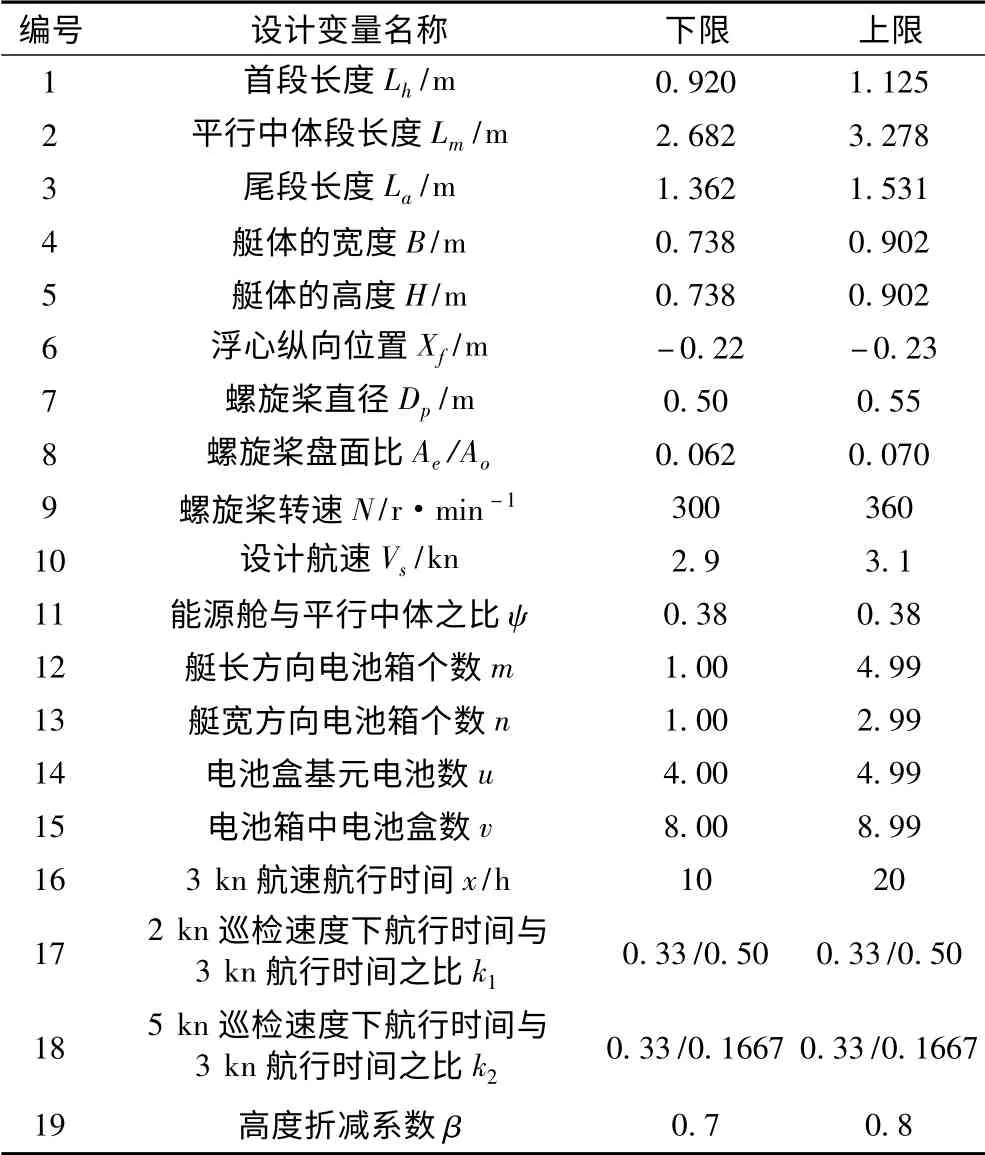
表1 設計變量范圍Tab.1 The range of design variables

1.2 目標函數

1.2.1 快速性目標函數

海軍系數是衡量船舶快速性能的重要參數，包括船舶阻力與推進性能優劣的綜合信息，是一個船舶快速性的綜合評價因子。參照海軍系數，快速性優化目標函數為:

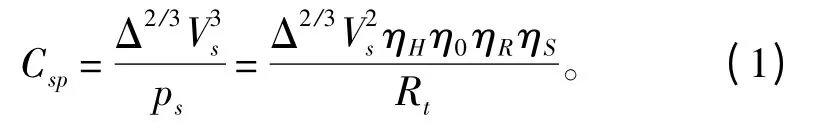
由于UUV 設計航行水深一般遠遠大于一個艇長，所以忽略興波阻力的影響，則總阻力Rt由摩擦阻力Rf、粘壓阻力Rpv、附體阻力Rap三部分組成。

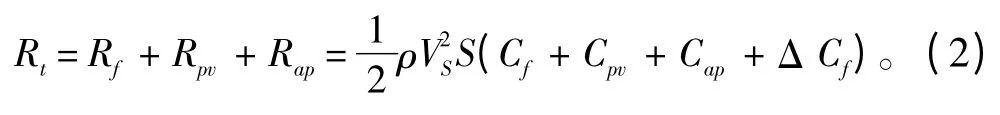
式中:Δ 為排水量;VS為設計航速;Rt為總阻力;ηH為船身效率;η0為螺旋槳敞水效率;ηR為相對旋轉效率;ηS為軸系傳送效率;ρ 為海水密度(取t=15℃時，ρ=1.025×103kg/m3);S 為濕表面積;Cf為摩擦阻力系數;ΔCf為粗糙度補貼系數，一般取0.4×10-3;Cpv為粘壓阻力系數;Cap為附體阻力系數。

1.2.2 能源系統目標函數

UUV 用電主要由動力電和控制電組成，動力電主要用于船舶螺旋槳和舵機耗電，控制電主要用于UUV 聲吶探測等設備用電，動力電的工作電壓為100 V，控制用電電壓為24 V。

考慮到性能好的能源艙的設計需要有較高的能源儲備系數以保證UUV 的航行安全，能源艙的能重比越大表示單位重量下所提供的電能越大，控制電路和動力電路的效率越高越好。綜合以上因素，本文選取5 個子目標函數構成能源系統的總目標函數。

1)控制電電路效率η1

滿足方程如下:

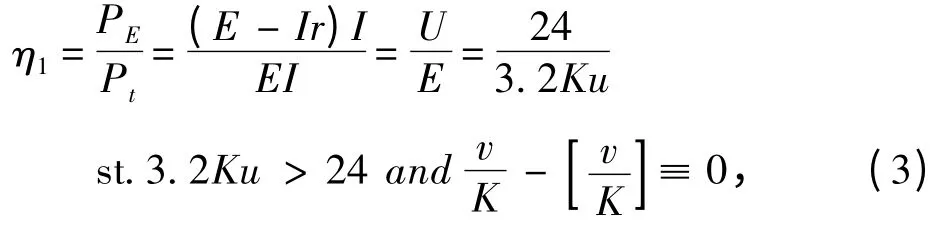
式中K 為達到控制用電電壓24 V 所串聯的電池盒個數。

2)動力電電路效率η2

滿足方程如下:

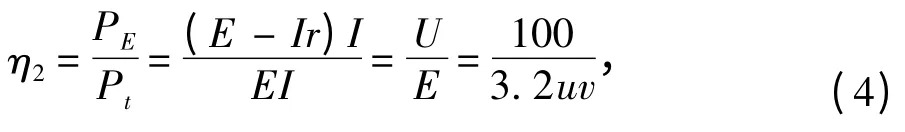
st.3.2uv ＞100。

3)控制電儲備能源系數λ1

滿足方程如下:

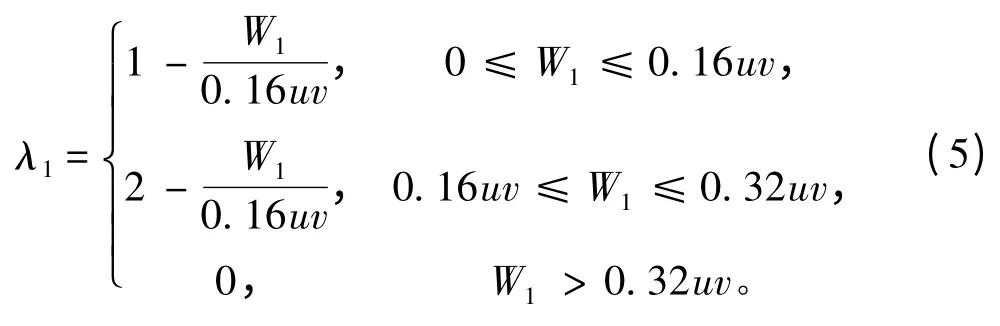
4)動力電儲備能源系數λ2

滿足方程如下:

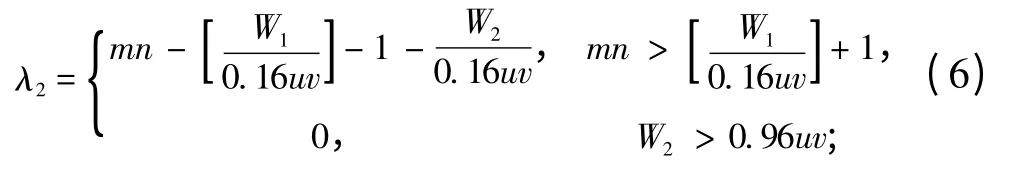
式中:W1為控制電功耗;W2為動力電功耗。

5)能源艙的能重比μ

滿足方程如下:

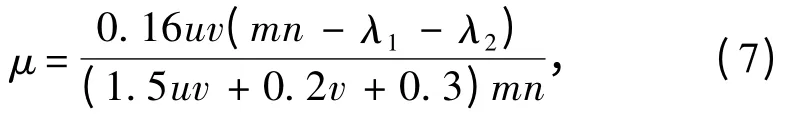
本文采用冪指數乘積的形式構成能源系統的總目標函數Cen:

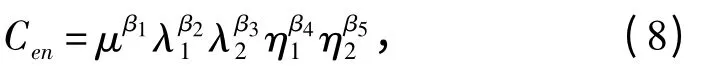
式中β1，β2，β3，β4，β5＞0 為對應子目標函數的權重，且β1·β2·β3·β4·β5=β，其中β 為能源系統總目標函數的權重。

1.2.3 綜合目標函數

分別對快速性和操縱性的目標函數設置權重α及β，且α·β=1。則綜合目標函數為:

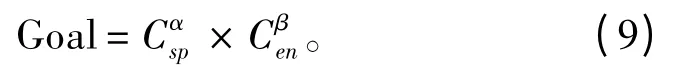
1.3 約束條件

1.3.1 等式約束條件

1)浮性約束，UUV 優化得到排水量與設計排水量一致

2)推力阻力平衡約束，螺旋槳有效推力與艇體航行阻力相等:

3)轉矩平衡約束，主機供給螺旋槳的轉矩等于螺旋槳所承受的水動力轉矩:

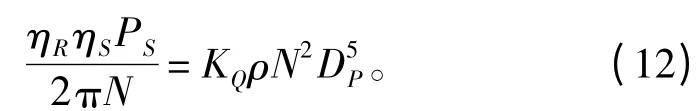
1.3.2 不等式約束條件

1)航程約束保證在設計航速下航程能達到100 km

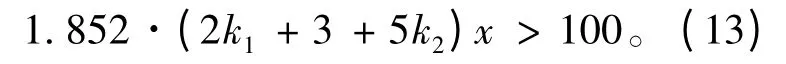
2)能源艙空間約束

艇長方向:

艇寬方向:

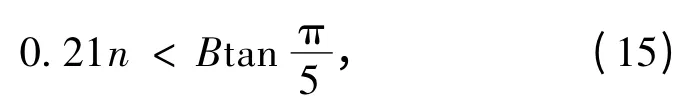
艇高方向:

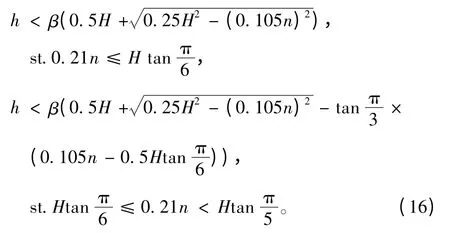
3)能源艙能源約束

考慮到電池箱外部電路約5%的能源損耗，將電池儲備能源進行了折減:

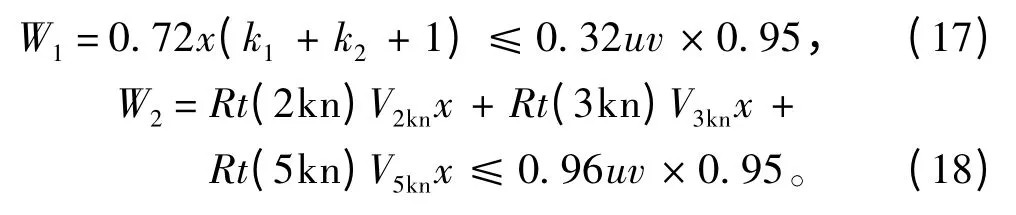
2 算法可靠性分析

2.1 優化計算

為了進行優化計算，首先需要定義各目標權重:

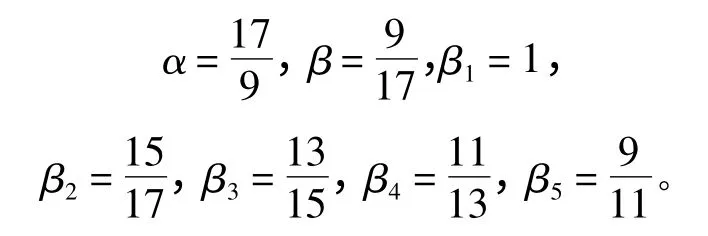
在1 臺計算機(主頻2.80 GHz，內存3.49 GB，硬盤1 TB)上進行基于10 000 代遺傳算法的優化計算，共計算3 次，取最好值作為該遺傳算法的最終結果(見表2)。

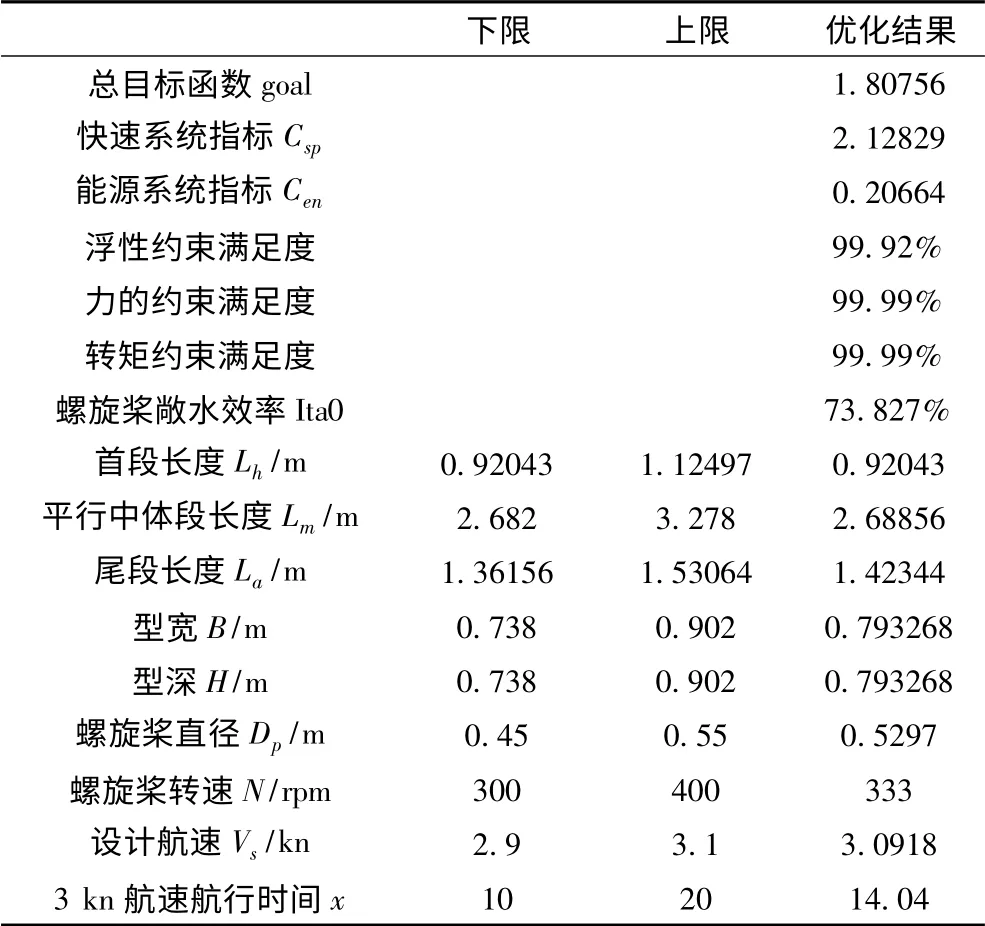
表2 優化算法計算結果Tab.2 The calculation results of optimization algorithms

2.2 算法可靠性分析

通過計算發現，多次運算后，結果均有小范圍的波動，但波動相對較小，各約束的滿足程度均達到99.9%以上，說明該優化方法計算結果穩定可靠，計算精度高，能較好地解決此類優化問題。

3 變量敏感度分析

艇體的首段長度、中段長度、尾段長度、回轉體直徑是艇體的主尺度，貫穿整個優化系統，對艇體快速性和能源系統均有影響。在快速性系統中，主尺度影響艇體的總阻力;在能源系統中，主尺度主要影響能源艙的體積。螺旋槳的直徑和轉速主要影響螺旋槳的敞水效率，設計航速航行時間主要影響UUV 的續航力。因此認為在整個優化系統中，這7 個設計變量較其他設計變量而言敏感度較高。

為研究變量對優化系統的敏感性，選取艇體首段長度Lh、中段長度Lm、尾段長度La、回轉體直徑B、螺旋槳直徑Dp、螺旋槳轉速N 和3 kn 航速航行時間x 共7 個設計變量為研究對象，分別將7 個設計變量離散，利用基于遺傳算法的綜合優化系統對剩余設計變量進行優化計算，并繪制出7個變量對該優化系統的敏感度曲線。

本文的敏感度曲線包括快速性目標函數Csp、能源系統目標函數Cen和綜合目標函數Goal 隨各設計變量變化的曲線。

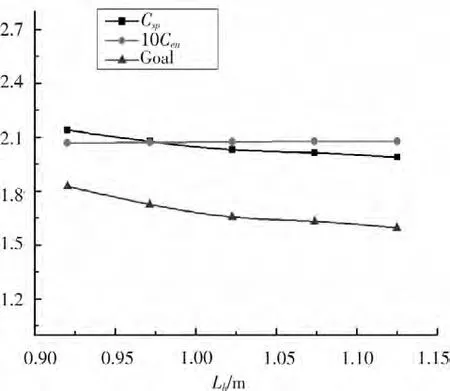
圖1 Lh 對優化系統的敏感度曲線Fig.1 Lh′s sensitivity curve to optimize system

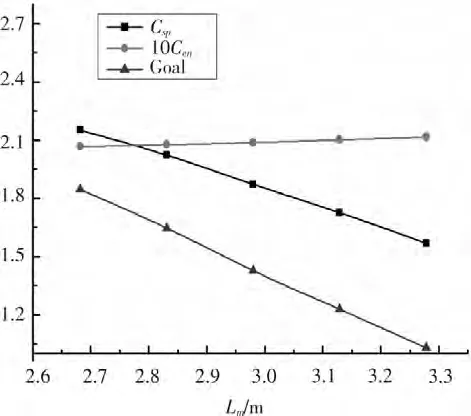
圖2 Lm 對優化系統的敏感度曲線Fig.2 Lm′s sensitivity curve to optimize system

圖3 La 對優化系統的敏感度曲線Fig.3 La′s sensitivity curve to optimize system

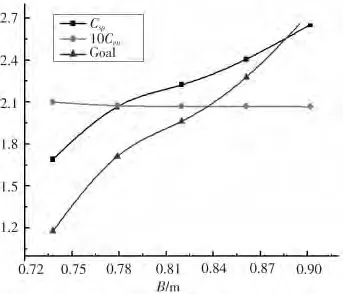
圖4 B 對優化系統的敏感度曲線Fig.4 B′s sensitivity curve to optimize system

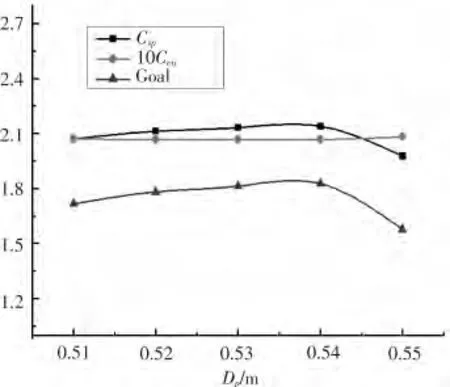
圖5 Dp 對優化系統的敏感度曲線Fig.5 Dp′s sensitivity curve to optimize system

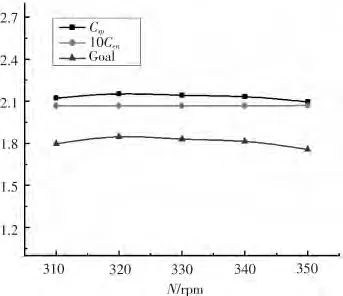
圖6 N 對優化系統的敏感度曲線Fig.6 N′s sensitivity curve to optimize system

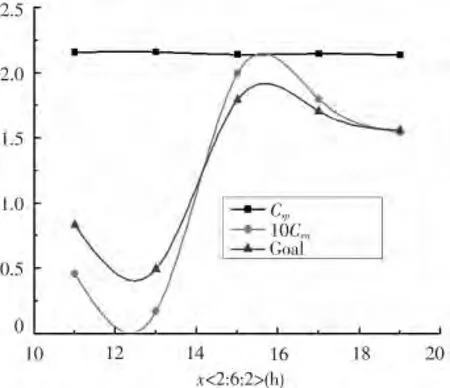
圖7 x 對優化系統的敏感度曲線Fig.7 x′s sensitivity curve to optimize system

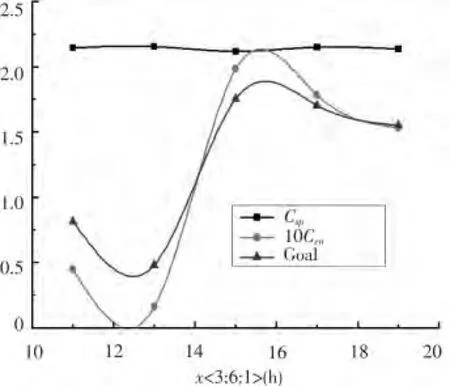
圖8 x 對優化系統的敏感度曲線Fig.8 x′s sensitivity curve to optimize system

圖1 ～圖6 分別為艇體首段長度Lh，中段長度Lm，尾段長度La，回轉體直徑B，螺旋槳直徑Dp，螺旋槳轉速N 所對應的敏感度曲線。

圖7 是當2 kn，3 kn 和5 kn 航行時間之比為2∶6∶2時的3 kn 航行時間x 對應的敏感度曲線。

圖8 是當2 kn，3 kn 和5 kn 航行時間之比為3∶6∶1時的3 kn 航行時間x 對應的敏感度曲線。

從圖1 ～圖6 可以看出，對于艇體的幾何外形參數而言，平行中體段長度和回轉體直徑對該優化系統的敏感度較大，而首、尾段長度對優化的敏感度較小，觀察曲線可以發現，艇長越小、回轉體直徑越大，快速性越好，因而總目標函數值也越大。對于螺旋槳參數而言，螺旋槳直徑在0.54 m 左右，轉速在320 r·min-1左右時具有更好的推進性能。

從圖7 和圖8 可以看出，3 kn 航速航行時間x主要影響了UUV 的能源系統，而對快速性影響不大。2 種不同的時間配比情況下，能源系統目標函數曲線均呈現隨x 的增大而分段遞減的趨勢。并且通過觀察曲線可以發現，能源系統目標函數的走勢對總目標函數的走勢也有很大的影響。

因此，算法可以進一步改進，選取敏感度大的設計變量并進行并行劃分，然后再利用遺傳算法進一步優化，便可以使優化更精確。

4 結 語

本文主要研究了UUV 快速性和能源系統的綜合優化問題。首先，本文從快速性和能源系統兩方面構造了UUV 綜合優化數學模型，該模型較好的將優化問題數學化，變成了一個多目標、多約束、多變量的工程優化設計問題。其次，本文構造了基于遺傳算法的綜合優化方法，并進行了基于遺傳算法的優化計算。計算的結果表明:其計算結果穩定可靠、約束滿足程度好。最后本文選取7 個設計變量進行離散，分析了數學模型中的不同設計變量對該優化系統的敏感度，為進一步構造分層并行方法提供依據。今后可以利用此方法，分析數學模型中的目標函數類型及性能指標權重對該優化計算問題的影響［8］。

［1］FIRDAUS A，MATTHIEU F，ANDREW R.Design optimisation of an unmanned underwater vehicle［J］.Journal of Engineering Science and Technology，2007:119.

［2］HOU W，KENDALL L C，DAVID K.et al.Using unmanned underwater vehicles as research platforms in coastal ocean studies［J］.Journal of Ocean University of Qingdao，2003，2(2):211 -217.

［3］FLETCHER B.A vision for navy UUV development［C］//OCEANS 2000 MTS/IEEE Proceedings，2000.

［4］王其.水下無人作戰平臺主體外形低阻低噪綜合優化設計［D］.西安:西北工業大學，2003.

［5］PAN Bin-bin，CUI Wei-cheng，LENG Wen-hao. Multidisciplinary design optimization of surface vessels［J］. Journal of Ship Mechanics，2009，13(3):378 -387.

［6］李密，高雷，孫筱波，等.高速單體船航行性能與結構力學特征綜合優化初步研究［J］.艦船科學技術，2009，31(1):47 -52.Li Mi，GAO Lei，SUN Xiao-bo，et al. On the overall optimization of navigational performance and structure characteristic for one kind of the high-speed ships［J］.Ship Science and Technology，2009，31(1):47 -52.

［7］李學斌.多目標遺傳算法在水面船舶快速性優化設計中的應用［J］.江蘇科技大學學報(自然科學版)，2008，22(5).LI Xue-bin.Application of multi-objective genetic algorithm to the optimal and fast design of surface ship［J］.Journal of Jiangsu University of Science and Technology (Natural Science Edition)，2008，22(5).

［8］陳鵬，楊松林，劉福偉，等. 基于并行遺傳混沌方法的UUV 性能綜合優化分析［J］. 艦船科學技術，2013，35(8):66 -71.CHEN Peng，YANG Song-lin，LIU Fu-wei，et al. The comprehensive optimization of UUV′s performance based on parallel genetic chaos method［J］. Ship Science and Technology，2013，35(8):66 -71.