卡爾曼濾波在變形監(jiān)測中的應(yīng)用

金廷文

（中交三航局第二工程有限公司，上海 200122）

0 引言

卡爾曼濾波器是一個“最優(yōu)化自回歸數(shù)據(jù)處理算法”，它是在線性最小方差估計的基礎(chǔ)上的數(shù)學(xué)結(jié)構(gòu)比較簡單的最優(yōu)線性遞推濾波方法。卡爾曼濾波的實質(zhì)是由量測值重構(gòu)系統(tǒng)的狀態(tài)向量，它以“預(yù)測—實測—修正”的順序遞推，根據(jù)系統(tǒng)的量測值來消除隨機干擾，再現(xiàn)系統(tǒng)的狀態(tài)，或根據(jù)系統(tǒng)的量測值從被污染的系統(tǒng)中恢復(fù)系統(tǒng)的本來面目[1-2]。

從以上分析可以看出卡爾曼濾波就是在有隨機干擾和噪聲的情況下，以線性最小方差估計方法給出狀態(tài)的最優(yōu)估計值，卡爾曼濾波是在統(tǒng)計的意義上給出最接近狀態(tài)真值的估計值。因此，在變形監(jiān)測中，卡爾曼濾波可以利用新的變形監(jiān)測觀測值，通過不斷地預(yù)測和修正即可估計出系統(tǒng)新的狀態(tài)值，這正適用于處理多期重復(fù)觀測的監(jiān)測網(wǎng)的觀測數(shù)據(jù)，從而對監(jiān)測網(wǎng)進行形變分析。

1 卡爾曼濾波的模型

卡爾曼濾波模型由狀態(tài)方程（1）和觀測方程（2）組成[3]，基本的數(shù)學(xué)模型如下[1]：

式中：Xk為k時刻系統(tǒng)狀態(tài)向量；φk，k-1為k-1時刻到k時刻的系統(tǒng)狀態(tài)轉(zhuǎn)移矩陣；Γk，k-1為k-1時刻到k時刻系統(tǒng)狀態(tài)噪聲輸入矩陣；Ωk為輸入噪聲；Wk為觀測值的噪聲序列；Zk為k時刻系統(tǒng)觀測向量；Hk為k時刻系統(tǒng)的觀測矩陣，Δk為k時刻系統(tǒng)觀測噪聲。

通過該數(shù)學(xué)模型就可以進行狀態(tài)估值Xk的求解了。

2 變形監(jiān)測濾波模型的建立

2.1 狀態(tài)方程

變形監(jiān)測是一種動態(tài)測量，物體的變形就是物體的空間位置隨時間的改變，也就是在一定時間內(nèi)發(fā)生的位移。傳統(tǒng)的數(shù)據(jù)處理方法是從靜態(tài)的角度對各期數(shù)據(jù)觀測值進行單獨平差，然后對各期的變形量加以比較，這樣就反映了監(jiān)測點在相應(yīng)時間內(nèi)的變形情況。而為了更好地了解被研究物體的變形狀態(tài)，僅僅求得一定時間內(nèi)的變形量是不夠的，還應(yīng)知道監(jiān)測點在某時刻的沉降速度甚至加速度，從而可以預(yù)測其未來的趨勢。

設(shè)有一組變形監(jiān)測點，其位移過程是一個隨機過程。在tk時刻的位置用xk表示，形變速度用vk表示，運動加速度用ak表示，動態(tài)噪聲用Ωk表示。對這些狀態(tài)參數(shù)常用的運動模型是將監(jiān)測點的位置和形變速度及形變加速度都視作狀態(tài)參數(shù)，而將形變加速度的變化率視作動態(tài)噪聲，運動方程為公式（3）：

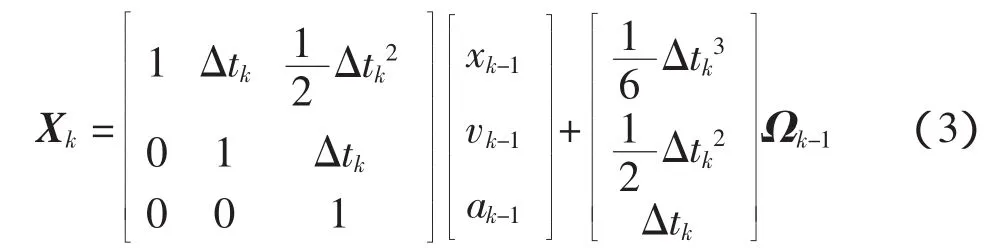
Ωk為三維形變加速度的動態(tài)噪聲矩陣，Δtk為tk時刻和tk-1時刻的時間差。

對應(yīng)到狀態(tài)方程（1）中，可得

2.2 觀測方程

變形監(jiān)測中通常觀測的是監(jiān)測點的變形情況，即監(jiān)測點在tk時刻和tk-1時刻位置，由兩個時刻的空間位置得到的位移向量即為形變量，其觀測方程與方程（2）相同。

以上公式為一維動態(tài)監(jiān)測網(wǎng)（沉降監(jiān)測）適用公式，如果是二維平面監(jiān)測網(wǎng)或三維空間監(jiān)測網(wǎng)，需要根據(jù)不同的觀測值確定模型中的Xk和Zk的維數(shù)，建立正確的濾波模型。

3 實例分析

本算例以港珠澳大橋東人工島暗埋段沉降監(jiān)測數(shù)據(jù)為原始數(shù)據(jù)，暗埋段地基通過降水、堆載預(yù)壓處理后，打設(shè)PHC樁，并在PHC樁頂部鋪設(shè)碎石墊層及澆筑混凝土墊層。

為了監(jiān)測暗埋段的沉降情況，每節(jié)段暗埋段共布設(shè)4個監(jiān)測點，位于4個角點處，觀測得到的數(shù)據(jù)為沉降量的時間特征，在進行數(shù)據(jù)處理前，要進行數(shù)據(jù)的初級處理，將沉降量的時間特征化算到累積沉降量的時間特征。選取其中一個點（點號CE3-1-N2）的觀測數(shù)據(jù)作為處理實例，各期觀測值沉降量見表1。

表1 點CE3-1-N2沉降監(jiān)測數(shù)據(jù)Table 1 The settlement data of point CE3-1-N2

結(jié)合運動方程及觀測方程，Zk為一維的累積沉降量觀測值，則Hk= [1 0 0]，由于速度值是狀態(tài)參數(shù)，而速度的初始值需要前兩期的數(shù)據(jù)共同來確定，則從第三期開始進行濾波處理。數(shù)據(jù)初始值X0的協(xié)方差陣及觀測噪聲的協(xié)方差陣，根據(jù)變形監(jiān)測的精度要求及測量規(guī)范，按照變形監(jiān)測等級給定初始值X0的方差為0.5 mm2，權(quán)逆陣為單位陣，則初始值的協(xié)方差陣為：

濾波過程分兩步進行，第1步是對前15期數(shù)據(jù)進行濾波處理，計算濾波值與實測值之差，比較數(shù)據(jù)見表2；第2步是對后6期數(shù)據(jù)進行濾波預(yù)測，計算預(yù)測值與實測值之差，比較數(shù)據(jù)見表3。

表2 前15期數(shù)據(jù)實測值與濾波值之差計算表Table 2 The difference between the observation value and the filtering value of the first 15 data mm

表3 后6期數(shù)據(jù)實測值與預(yù)測值之差計算表Table3 Thedifferencebetween theobservation data and theforecast data of thelast 6 data mm

另外，對數(shù)據(jù)進行五次多項式擬合分析，并將觀測值、濾波值及多項式擬合值進行作圖比較，形成圖形見圖1。

圖1 濾波值與五次多項式擬合值比較圖Fig.1 Comparison chart of filtering value and five polynomial value

4 結(jié)語

通過實例計算和分析后得到以下結(jié)論：

1）卡爾曼濾波是一個不斷的預(yù)測、修正的過程，修正由于噪聲引起的數(shù)據(jù)突變，使數(shù)據(jù)更符合實際變形趨勢，并且只要有新的測量成果，就可以進行濾波處理，計算出最新的濾波值，便于實時處理觀測值。

2）卡爾曼濾波值在原始數(shù)據(jù)基礎(chǔ)上進行修正得到的最優(yōu)估計值偏離原始值很小，則在考慮沒有觀測錯誤和粗差的情況下，所建立的濾波模型是合理的，可靠的，它能較好地模擬動態(tài)系統(tǒng)的變化規(guī)律，能有效改善原始觀測數(shù)據(jù)的精度。

3）從表2數(shù)據(jù)分析，卡爾曼濾波值與觀測值之間最大差值為12期的0.109 mm，其余差值均小于0.1 mm，說明卡爾曼濾波能較好地反應(yīng)出暗埋段實際的沉降情況，對沉降監(jiān)測能有效剔除噪聲的作用。

4） 通過表3可以看出，預(yù)報值偏差最大為-1.608 mm，最小為-0.008 mm，說明卡爾曼濾波具有較強的預(yù)報作用。

5）從圖1中濾波值與多項式擬合比較不難看出，濾波值與觀測值重合度高，而五次多項式擬合值偏離觀測值大小不一，說明濾波值比多項式擬合的精度要高。