地下水位動態序列分析與預報研究

鄒 曄，胡 瑩，朱世芳

（山東省魯南地質工程勘察院，山東兗州272100）

地下水位動態序列分析與預報研究

鄒 曄*，胡 瑩，朱世芳

（山東省魯南地質工程勘察院，山東兗州272100）

根據地下水水位動態資料的特點，將地下水位非平穩時間序列分解為趨勢項函數、周期項函數和隨機項3部分，并疊加后建立組合數學模型，對地下水水位動態進行預測。最后通過實例檢驗，此種建模和預報理論取得了較好的效果。

地下水水位動態；非平穩時間序列；預測

1 概述

地下水動態取決于地下水的補給、徑流與排泄條件，是受地形地貌、地層巖性、氣象和水文等自然因素和人工開采、灌溉、排水等人為因素綜合作用的結果。地下水動態反映了地下水要素隨時間變化的狀況，為了合理利用地下水或有效防范其危害，必須掌握地下水動態。

目前國內外已經有很多學者研究了采用隨機性數學模型進行地下水水位動態的預測，其中受到大家公認的方法主要包括回歸分析法、頻譜分析法和時間序列分析法等。在各種隨機模型中，無論是頻譜分析法還是時間序列分析法，都要求地下水動態序列滿足平穩性條件，而實際中的地下水動態序列，由于人為干擾因素越來越大以及觀測時間的有限性，絕大部分序列都不滿足平穩性條件，而是存在一個趨勢項。此外，由于各種隨機因素的作用，單一的周期加趨勢項模型必然會產生大量殘差，即隨機項，從而使預報的精度大大降低。為此本文嘗試運用參數模型方法研究非平穩性地下水動態序列。

2 非平穩時間序列分析

2.1 非平穩時間序列模型

所謂非平穩時間系列，即表示統計性質隨時間而異的存在非常廣泛的那一類物理數據，在實際問題中經常遇到的時間序列一般都是非平穩的。由于非平穩時間序列的一般性和復雜性特點，對它至今尚無統一處理的一般方法。

設D（t）是時間t的確定性函數，R（t）是一個各態歷經的平穩隨機過程，通常可以采用加法模型來研究非平穩過程，作為實際物理過程的近似，

由H（t）的測量數據，用一種統計的方法估計函數D（t）所含的一些參數，識別、提取、預報趨勢函數項D（t）。人們把這樣一類方法，稱為參數模型方法。

在時間序列分析中，識別、提取趨勢項D（t），是很重要的一項工作。為了提取D（t），一般假定D（t）由2部分組成，即：

式中：T（t）——實際測量數據隨時間t變化的主值函數項；

P（t）——由實測數據中可分離出來的周期函數項。

因此，一個非平穩時間序列可以認為是由趨勢成分、近似周期成分和平穩隨機成分組成，而平穩時間序列則要求統計參數的期望值與方差不隨時間改變。

2.2 非平穩時間序列建模

2.2.1 建模思路

非平穩水位動態序列H（t）是由趨勢成分T（t）、近似周期成分P（t）和平穩隨機成分R（t）組成，其可表示為3個組成部分之和，表達式為[1]：

H（t）=T（t）+P（t）+R（t）

在非平穩水位動態模型中，趨勢項T（t）反映變量的多年變化趨勢；周期項T（t）反映變量的周期性變化。趨勢項、周期項這2項反映了時間序列變量變化中的確定性成分，把這2項分離出去，余下的就是隨機項了。隨機項可用平穩時間序列來分析，其可分為2項：平穩時間序列項S（t）和純隨機項N（t），即：

R（t）=R（t）+N（t）

其中純隨機項N（t）作為白噪聲來處理。

將時間序列變量分解成3個組成部分之后，就可按各組成項的變化規律對未來時刻進行外推，再將各項合成作出預報。

2.2.2 地下水水位動態時間序列模型的建立

（1）趨勢項分析：趨勢項是指在時間序列中，序列穩定而規則的變動，即隨時間的推移對平均值來說增大或減小的趨勢，其可能是線性的，也可能是非線性的。趨勢項數學模型的結構基本上由人們的經驗判定，當無法判定趨勢項應采用何種形式的數學結構時，通常用確定性模型擬和趨勢成分T（t），用逐步回歸方法對模型系數加以求解。

對于趨勢分量T（t）可用多項式逼近，即：

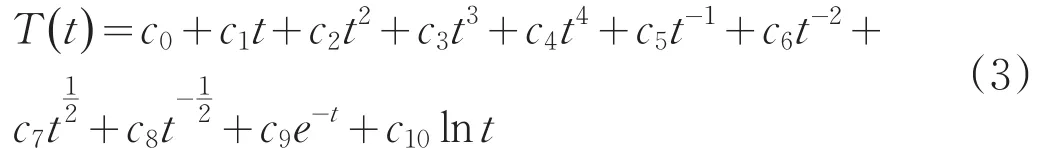
由此，可采用多元回歸方法確定待定系數c0，c1，c2，…，c10和階數。其具體求解方法通過編程序統一處理來實現。如果經逐步回歸計算，回歸系數全為零，可以認為（3）式無趨勢項T（t）。

（2）周期項分析：

①頻譜分析方法：周期分量是序列隨著時間的推移而呈現出的周期性成分。時間序列分離趨勢之后，將剩余的序列P（t）=H（t）-T（t）進行周期分析。識別和提取周期項P（t）的方法有方差分析、頻譜分析和周期圖分析等，這里主要采用頻譜分析法。

頻譜分析是利用傅立葉級數把某個資料的時間序列表示成無數個不同周期的簡諧波和的形式來分析序列變化規律的一種方法。對序列P（t）可用L個波疊加的形式表示其周期項[2]：

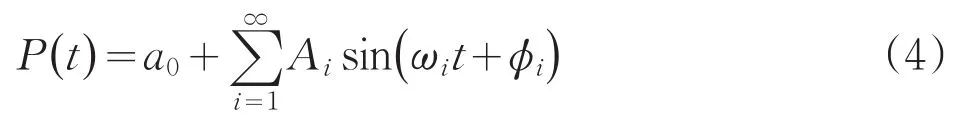
其中的每個項為一個分波，分別稱Ai，ωi，φi為第i個分波的振幅、頻率和相位，a0為一常數。因為

sin( ) ωit+φi=sinωitcosφi+cosωitsinφi

并令：

ai=Aisinφibi=Aicosφi

則P（t）可以改記為：

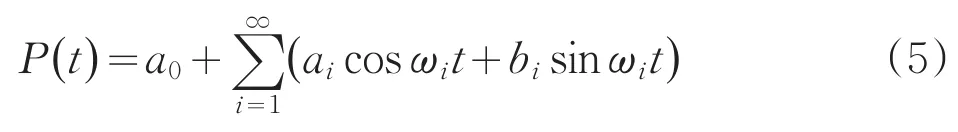
由于觀測資料的有限性，無法進行無窮分波，因此一般假定P（t）有K個分波（試驗周期個數），即：

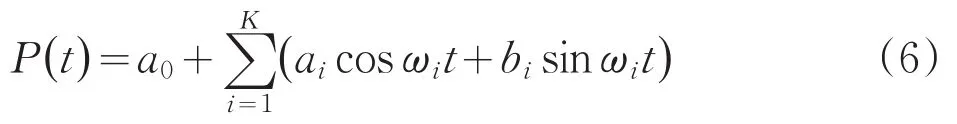
對于給定的時間序列可用以下的方法來確定a0，ai，bi，i=1，2，…，K。設有n個水位H（t），t=1，2，…，n，n為樣本的長度，除去其趨勢項T（t）后，余下的序列記為P（t），即P（t）=H（t）-T（t），t=1，2，…，n，又認為K個分波各有年的周期，即第i個分波，周期為：

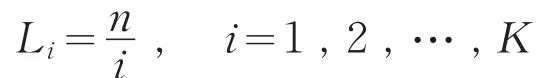
因而第i個分波的頻率為：

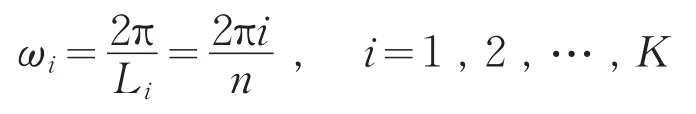
于是：

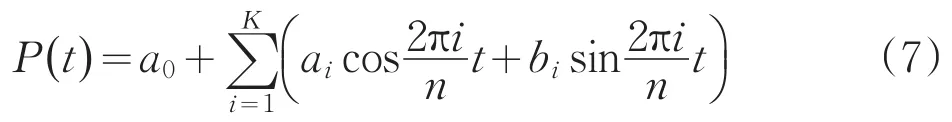
可以采用最小二乘法來確定系數a0，ai，bi，通過一系列推導，可以求得：

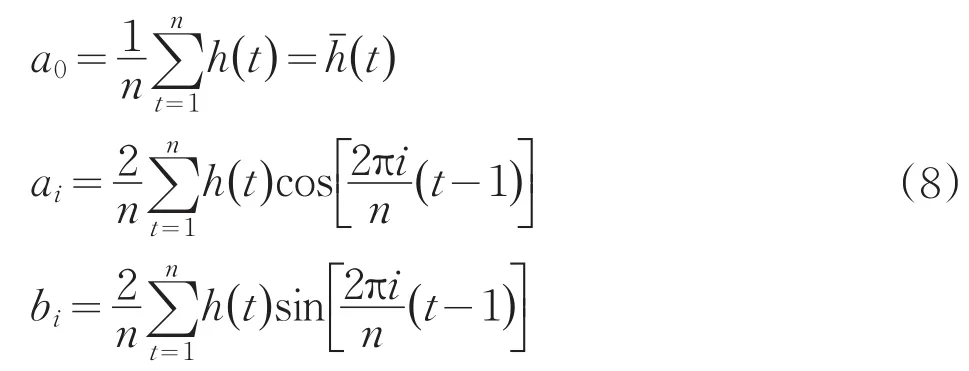
如何從上述求得的各分波系數ai，bi中選取主要周期。常用下面2種方法推求。

②主要周期判斷：本次分析用振幅的大小判斷主要周期。

因：

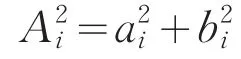
故：

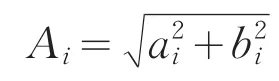
在顯著水平為0.05時，若：

則認為相應的第i個分波是主要周期，上式中的n為樣本長度，K為試驗周期個數，σ2為序列P（t）的方差，可用樣本方差S2來估計。通過推導能夠證明S2可用下式來計算：

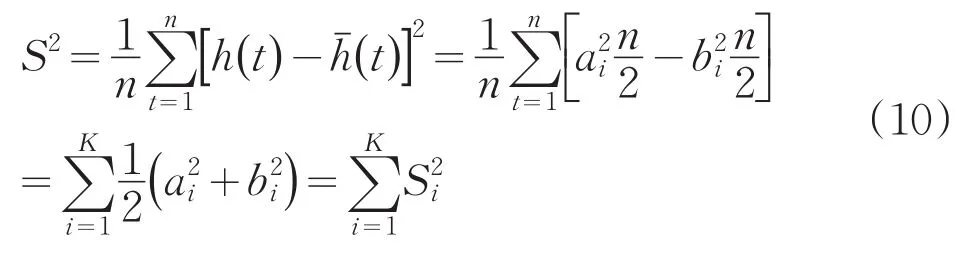
其中：

若A1，…，Ak中有M個分波滿足（9）式，則我們在（6）式中只保留相應的M個項即可，即最后求得P（t）的周期項為：

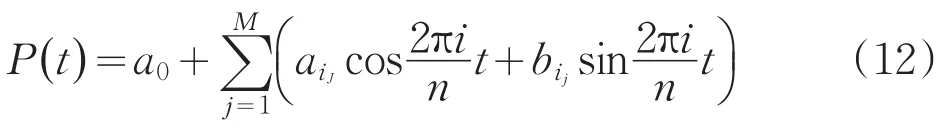
在實際應用中為節省工作量，通常在L個波中選取波動比較顯著的幾個諧波相加得到周期項，一般只需選取前6個顯著諧波就能滿足精度要求了。

（3）隨機項分析：隨機分量是指各時刻的序列值與前一個時刻或幾個時刻值存在著某種相關關系的成分。時間序列模型中，消除趨勢項和近似周期項后的剩余序列，即為平穩隨機系列項，此時，即可用平穩隨機模型方法來分析求解。

①求解數學模型：在數理統計中，我們已知回歸模型為：

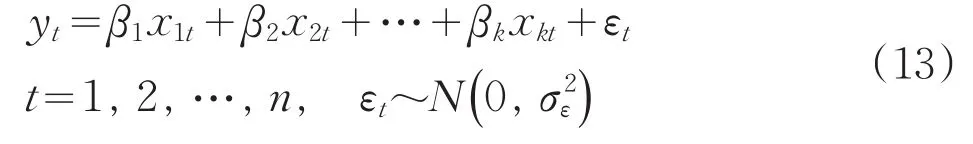
它表示觀測值yt對另一組觀測值（x1t，x2t，…，xkt）的相依性，上式可以視為由2部分組成，一部分取決于自變量（x1t，x2t，…，xkt），而另一部分則是隨機成分εt。觀測序列｛yt｝是假定為相互獨立或不相關的。

對時間序列xt=x（t）（假定屬平穩序列，且均值為零）有[3]：

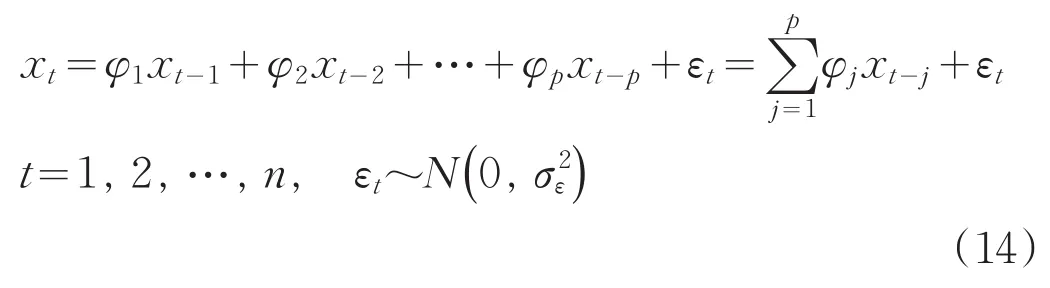
上式為p階自回歸模型，常記為AR（p），式中φ1，φ2，…，φp為待定常數，稱它們為自回歸系數，εt表示在量測過程中存在的隨機干擾和未來預報中出現的誤差。我們假定t時的觀測誤差εt與t以前的觀測值xt-j，j=1，2，…，p獨立，因而有：

②自回歸系數的確定：自回歸系數φ1，φ2，…，φp的確定有2條途徑。

其一是用xt-i乘（14）式兩邊，得到：

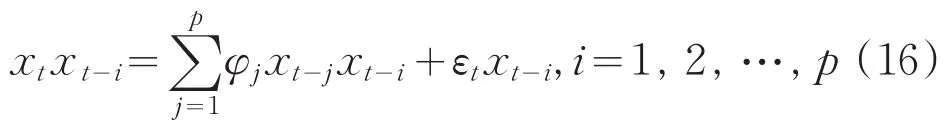
上式兩邊取數學期望，并利用（15）式得：

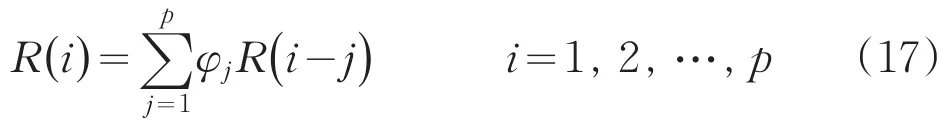
此即一組p階線性方程：

式中：R（1），R（2），…，R（p）可以用估計值r（1），r（2），…，r（p）來代替，于是從理論上講由（18）式便可以解出φ1，φ2，…，φp。

根據x1，x2，…，xN為各態歷經平穩時間序列的假定，可以用下式估計相關函數r（τ）[4]：

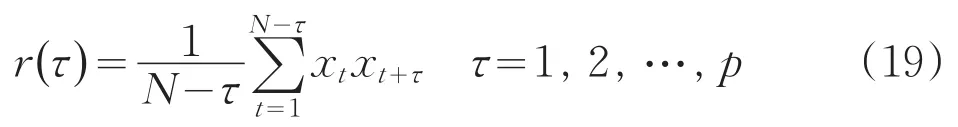
若x1，x2，…，xp未標準化，需先標準化如下：

然后對xb1，xb2，…，xbN使用（19）式。這樣，我們得到自回歸系數φ1，φ2，…，φp的相應估計值b1，b2，…，bp，它們滿足p階方程組：

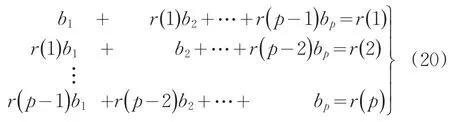
式中r（p）[r（τ）]即為相關函數R（p）[R（τ）]的估計值，見式（21）。

另一途徑用最小二乘估計的方法來決定（14）式中的系數φ1，φ2，…，φp，即選φ1，φ2，…，φp，使：

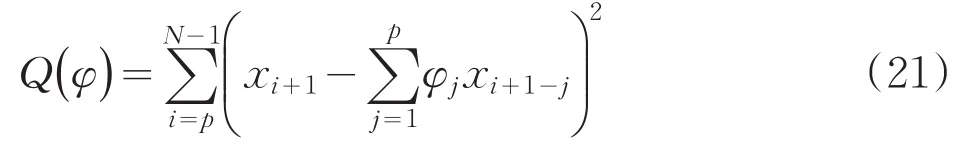
為最小值[5]。上式關于φj，j=1，2，…，p分別求偏導數，得：

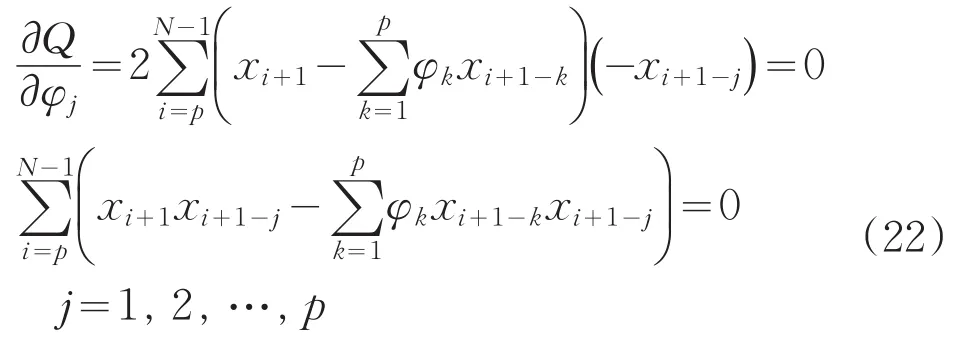
由各態歷經性的假定有：

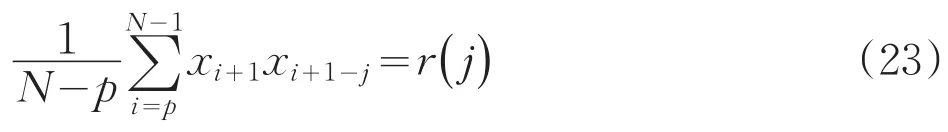
于是（22）式兩邊除以N-p，據（23）式，便得：

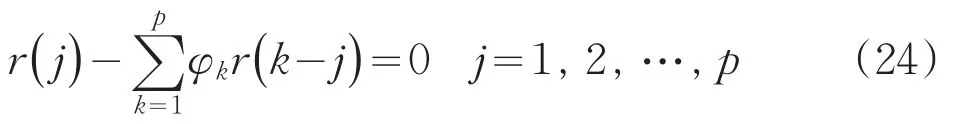
將φk改記為bk再展開后，它與（20）式完全一樣。

用各種代數方法求解方程組，得φ1，φ2，…，φp。

③自回歸模型階數p的確定：上面給出了自回歸模型（14）式，從上面的過程可以看出，如果取的階數p不同，則所得的模型也不同，因此便提出一個問題：究竟p應是多少，才可使得求出的自回歸模型（14）最佳？這實際上是個模型識別問題。

在使用上可以這樣考慮：給出一個誤差范圍，例如0.01，即（14）中的 ||εt＜0.01，然后對不同的p進行計算，直至滿足 ||εt＜0.01的那個p為止，最后所得結果便是所要的值。

3 實例驗證

為了驗證文中所提理論，筆者收集了某鉆孔1996～2012年的1224個水位值（每個月6個水位觀測值）作為建模數據，利用文章所提理論確定了模型，趨勢分析模型參數C0取3.510，C1取0.0042，其它模型參數結果見表1和表2。模型對1994～2012年水位進行了擬合，取得了較好的效果，實際水位與擬合水位對比圖見圖1，同時利用建立的模型對該鉆孔2013～2027年的水位進行了預報（見圖1）。

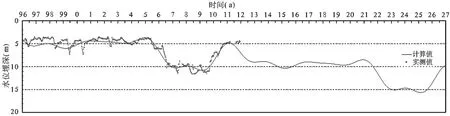
圖1 地下水位埋深動態擬合、驗證、預測曲線

表1 周期分析參數表

表2 自回歸模型參數表

4 結論

非平穩時間系列方法適宜樣本容量較大的地下水動態建模和預測，以容量大于100以上為佳，小樣本不足以全面反映地下水位動態的變化規律，不能有效地提取出真實的趨勢項和周期項，且受隨機干擾較大。同時該方法雖然在一定程度上考慮到了人為干擾的影響，但在偶然、大強度干擾下，預報結果會有一些誤差。

[1]張偉,徐建華,秦勇.非平穩性地下水動態序列分析及預測[J].工程勘察，2000(1):17.

[2]燕良東.地下水動態組合模型研究[D].遼寧：遼寧工程技術大學，2011.

[3]丁晶,劉全授.隨機水文學[M].北京：中國水利水電出版社，1997.

[4]安鴻志,時間序列分析[M].上海：華東師范大學出版社，1992.

[5]申鼎煊，隨機過程[M].湖北：華中理工大學出版社，1990.

TV641.74

A

1004-5716(2015)06-0182-04

2014-06-25

2014-07-03

鄒曄（1982-），男（漢族），江蘇宜興人，工程師，現從事水、工、環技術工作。