正八邊形多胞薄壁管吸能特性仿真和優化＊

白中浩，王飛虎，郭厚銳

（湖南大學 汽車車身先進設計制造國家重點實驗室，湖南 長沙 410082）

金屬薄壁結構以其成本低、吸能效率高等特點，在航空和汽車工業上的應用越來越廣泛．在過去數十年中，國內外針對金屬薄壁結構進行了大量的研究，從試驗、理論和數值分析方面探究了不同加載條件下的金屬薄壁結構的吸能特性．然而，過去大部分研究工作都集中在圓形、方形或矩形截面金屬薄壁結構上［1－4］．

近年來，具有多個胞元的新型薄壁結構受到關注［5－10］．Chen等人［5］于2001年率先在理論和數值分析方面研究了軸向加載下雙胞和三胞鋁制品結構的沖擊優勢．Zhang等人［6］比較研究了多胞結構和泡沫填充結構的吸能效率．Najafi等人［7］對不同截面方形多胞結構的吸能特性進行了研究．亓昌等人［8］研究了錐形多胞薄壁管斜向沖擊下的吸能特性．上述研究都表明：多胞薄壁結構與單胞或填充材料結構相比，具有更高的吸能效率．然而，到目前為止，關于非直角與板組成的多胞結構的研究較少．

Rossi等人［11］研究發現，在截面面積和厚度相同的情況下，八邊形薄壁結構比四邊形薄壁結構的平均碰撞力增加了25%，吸能變形量降低了20%．Fan等人［12］研究表明，八邊形薄壁管變形均勻，吸能特性較好．張宗華等人［13］研究了等周長的不同截面形狀多邊形薄壁結構的軸向沖擊性能，發現多邊形薄壁管的平均沖擊力和吸能特性隨著多邊形頂點的增加而提高，但八邊形以后基本趨于穩定．作者之前設計了一種八邊形逐級吸能結構，有效地改進了某越野車前縱梁的碰撞性能［14－15］，現針對八邊形薄壁結構以及多胞結構具有結構緊湊和高效吸能的特點，研究了一種邊對邊（two side to side，S2S）布置的正八邊形多胞管S2S結構，該結構同時結合了八邊形管的結構緊湊和多胞管的高比吸能特性．通過一系列仿真探討了不同截面形狀和結構參數對吸能特性的影響，并根據吸能特性指標對正八邊形多胞管S2S結構進行了優化，優化后其吸能特性明顯提高，為此類結構的優化設計和工程應用提供參考．

1 問題描述

1．1 物理模型

本文研究的對象為正八邊形多胞管S2S結構，如圖1所示．長度L為210mm，正八邊形截面邊長d為40mm，壁厚t都為1mm．底端采用固定支承，上端承受剛性墻以恒定速度軸向壓縮，速度大小為V．

圖1 正八邊形多胞管軸向壓縮示意圖Fig．1 Schematic diagram of octagon multi－celltubes under axial compression

1．2 結構吸能特性指標

一般來說，分析結構吸能特性的關鍵參數主要有：總吸能量（E）、比吸能（SEA）、平均壓潰力（Fav）、最大壓潰力（Fpeak）等．比吸能SEA是評價一個結構的能量吸收效率的指標，用來描述結構單位質量吸收的沖擊能量，可表示為：

式中：M為結構的質量；E為結構吸收的總能量，其值可以通過對力－位移曲線積分得到．

式中：d為結構的有效變形量．

平均壓潰力為Fav，其表達式如式（3）所示．由此式可以計算出平均壓潰力隨時間的變化趨勢．

最大壓潰力是指薄壁結構在壓潰過程中的初始壓潰載荷峰值，即薄壁結構與剛性墻初始接觸時峰值載荷Fpeak．

2 仿真模型

2．1 有限元建模

采用有限元軟件Abaqus／Explicit，建立了正八邊形多胞薄壁管模型．如圖2所示，頂部剛性平面以恒定的速度5mm／min軸向壓縮多胞管，多胞管底部與另一剛性平面焊接連接，底部剛性平面固定．多胞管采用四節點殼單元S4R模擬，綜合考慮精度和求解效率，殼單元沿厚度方向取5個積分點，單元特征長度取2．5 mm．多胞結構的材料為H300Lad鋼，密度ρ＝7 850 kg／m3，彈性模量E＝210GPa，泊松比ν＝0．3．H300Lad鋼材的真實應力－應變曲線如圖3所示．

圖2 正八邊形多胞管有限元模型Fig．2 Finite element model of octagon multi－cell tube

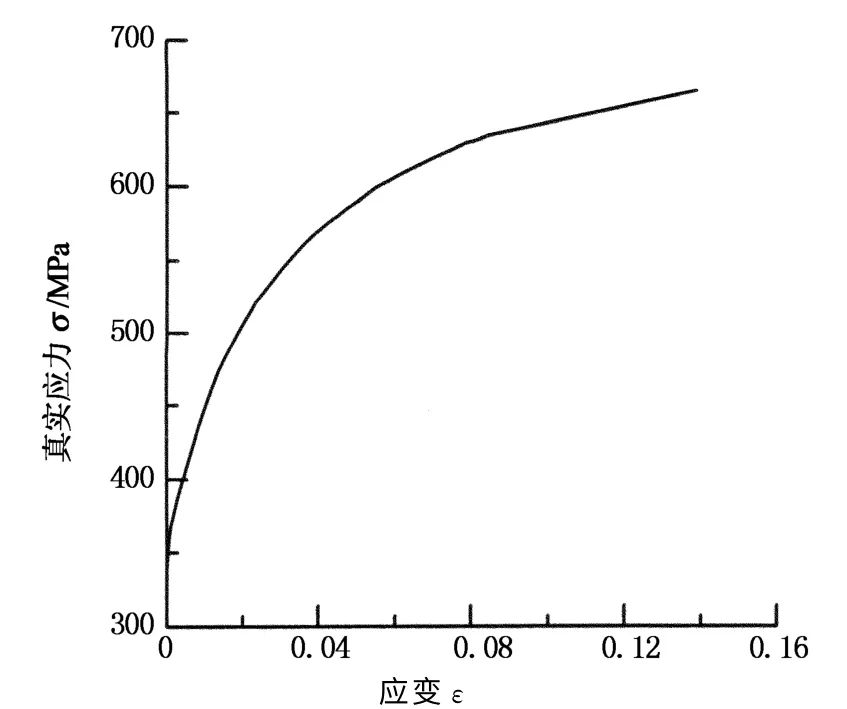
圖3 真實應力－應變曲線Fig．3 Ture strss－strain of specimens

2．2 有限元模型驗證

為了驗證有限元模型，根據文獻［12］的實驗模型參數，對正八邊形單胞管進行準靜態軸向壓潰仿真．圖4為本文有限元仿真結果與文獻［12］中的實驗結果對比，從圖中可以看出，力響應曲線的峰值、峰值出現時刻以及波動趨勢基本一致，變形模式方面存在一定的誤差，但誤差在可接受范圍內．因此，本文所建模型有效，可用于后續的研究．

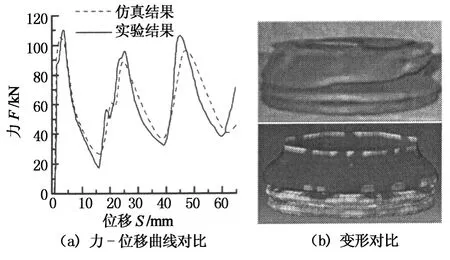
圖4 正八邊形單胞管仿真與試驗結果對比Fig．4 Simulation and experimental results comparison of octagon single－cell tubes

3 仿真結果與分析

3．1 截面形狀對吸能特性的影響分析

圖5為幾種幾何參數相同而截面形狀不同的正八邊形薄壁管示意圖，單胞管命名為SO（single－cell octagon）；2種不同截面形狀的四胞管分別命名為S2S（two side to side）和C2C（two corner to corner）；2種不同截面形狀的八胞管分別命名為S4S（four side to side）和C4C（four corner to corner）．通過對不同截面形狀的多胞管進行仿真分析，仿真結果如表1所示．

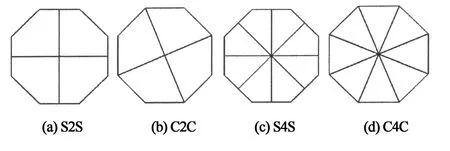
圖5 正八邊形薄壁管不同截面形狀示意圖Fig．5 Different cross sections shape of octagon thin－walled tubes

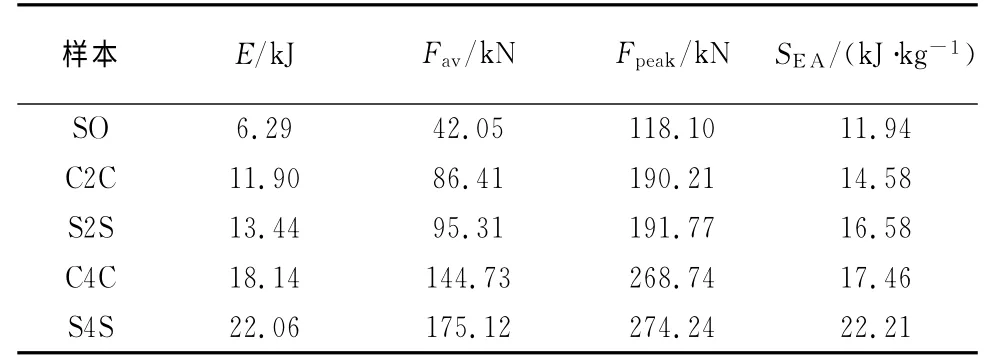
表1 多胞管數值分析結果Tab．1 Results of simulation for multi－cell tubes

從表1可以看出，平均壓潰力Fav隨著胞管數增加而增大．S4S 結構的平均壓潰力是SO 結構的4倍多．不同截面形狀的同胞數結構的平均壓潰力也不同，如同胞數的S2S結構與C2C 結構相比，平均壓潰力增加了10．3%．這是由于不同截面形狀導致出現不同的變形模式，當結構中連通邊為3的角單元在夾角小于120°時，隨著夾角的增大，平均壓潰力明顯增加［16］．

最大壓潰力Fpeak隨著薄壁管胞數的增加而明顯增大，S4S 結構的最大壓潰力Fpeak最大，達到了274．24kN，是SO 結構的2倍多，比S2S結構增加了43%．同時，S2S與C2C結構以及S4S與C4C 結構相比，最大壓潰力都略大些．其中，C4C 結構的最大壓潰力比S2S結構增加了40．14%．

多胞管的比吸能明顯高于單胞管，這是由于薄壁管胞數增加后，管內部增加了交叉板，這需要更多的能量來使之變形．此外，S2S與C2C結構以及S4S與C4C 結構相比，比吸能分別增加了13．7%和27．2%，這與結構的截面布置形式有關，同胞數管邊對邊的布置形式（side to side，見圖5（a）和圖5（c））相比角對角布置形式（corner to corner，見圖5（b）和圖5（d）），增加了拐角的數目，隨著拐角數目的增大，產生塑性變形需要耗散的總能量就越多．然而，C4C結構的比吸能比S2S結構只增加了5．3%，說明截面形式不同對多胞結構比吸能影響較大，邊對邊的布置形式比角對角布置形式的吸能效果更好．

3．2 結構參數對吸能特性的影響分析

在正八邊形多胞管S2S 結構基準模型的基礎上，研究結構幾何參數對多胞管吸能特性的影響．依據汽車車身結構中典型薄壁管件尺寸，各參數取值如表2所示．

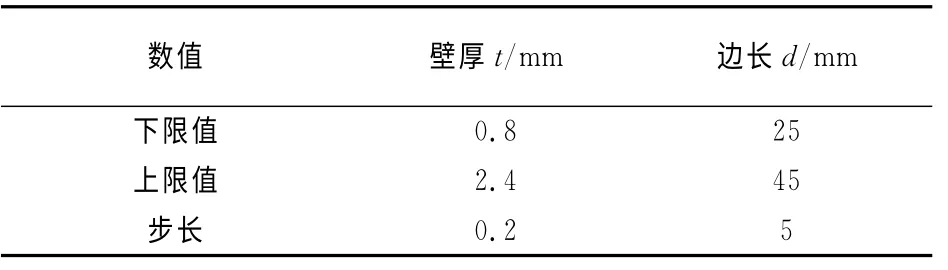
表2 正八邊形多胞管幾何參數取值Tab．2 Geometry parameters of octagon multi－cell tubes

3．2．1 壁厚對S2S結構的影響

保持截面尺寸不變，首先分析壁厚對S2S結構的影響．圖6為準靜態壓縮下壁厚t對多胞管S2S結構比吸能的影響．可以看出，隨著壁厚的增加，比吸能逐漸增大，增大幅度逐漸減小．如壁厚t從1．2 mm 增加到1．8 mm，比吸能增加了39．65%；t從1．8mm增大到2．4mm，比吸能只增加了13．77%．

壁厚對最大壓潰力的影響如圖7所示，最大壓潰力隨著壁厚的增加而單調上升，近似呈線性正相關．

圖6 壁厚對比吸能的影響Fig．6 Effect of wall thickness on SEA

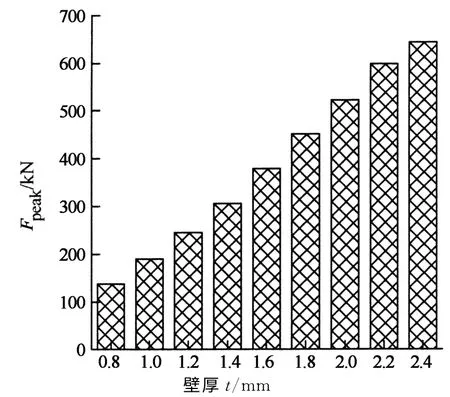
圖7 壁厚對最大壓潰力的影響Fig．7 Effect of wall thickness on peak force

3．2．2 截面尺寸對S2S結構的影響

圖8為截面邊長對S2S結構比吸能的影響．從圖中可知，隨著截面邊長的增大，比吸能單調減小，近似呈線性負相關．

截面尺寸對最大壓潰力的影響如圖9所示，隨著截面尺寸的增大，最大壓潰力略微增加．如邊長d從35 mm增大到45mm，最大壓潰力只增長了6．87%．

圖8 截面尺寸對比吸能的影響Fig．8 Effect of section size on SEA

圖9 截面尺寸對最大壓潰力的影響Fig．9 Effect of section size on peak force

總的來說，各結構參數對正八邊形多胞管S2S結構的吸能特性影響相互關聯，彼此制約，針對具體問題，有必要對S2S結構進行優化設計得到滿足需求的最優結構．

4 結構優化設計

4．1 優化問題定義

目前，提高薄壁結構吸能特性普遍采用2種方法：1）采用先進的高強度特性的材料；2）對壁厚、截面尺寸等參數進行優化．在碰撞過程中，常以最大吸能量為設計準則，但是，隨著不可再生能源的日益枯竭，輕量化設計已成為當前汽車安全性設計主要考慮的因素之一，因此比吸能更加全面地表征了結構的吸能性．此外，碰撞過程中薄壁結構的最大碰撞力也直接影響到車內乘員的安全性．

上述仿真結果表明，壁厚t和截面尺寸d對多胞管S2S結果的吸能特性影響明顯．為了進一步提高多胞管S2S結構的吸能特性，以多胞管S2S結構的壁厚t和截面尺寸d為優化參數；以比吸能SEA，平均壓潰力Fav以及最大壓潰力Fpeak為優化目標，定義多胞管S2S結構的多目標優化問題為：

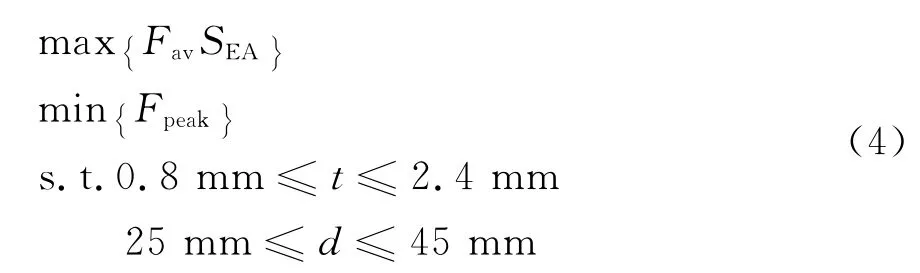
為了提高求解效率，優化過程采用二次多項式響應面模型代替有限元仿真分析，并通過優拉丁超立方試驗設計（DOE）方法設計9組仿真試驗，建立響應面模型．利用非支配遺傳算法（NSGA－Ⅱ）［17］尋求多目標優化問題（式（4））的帕雷托最優解，優化流程如圖10所示．

4．2 構建近似模型

近似模型的方法已經被證明是一種特別有效的方法，被廣泛應用于薄壁管的優化設計中，如響應面模型（RSM）［18］．本文基于優拉丁超立方試驗設計的試驗結果，利用逐步回歸方法得到優化目標關于兩個設計變量的二階多項式響應面模型的多元回歸方程為：

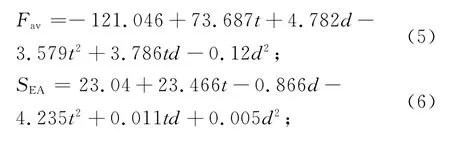
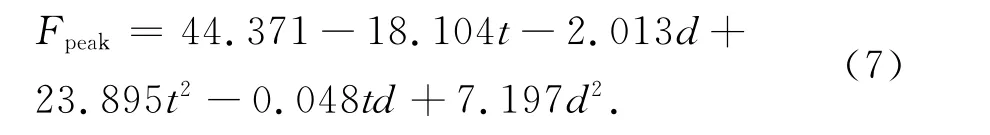
式中：Fav，SEA和Fpeak分別為正八邊形多胞管S2S結構的平均壓潰力、比吸能和最大壓潰力；t和d分別為多胞管的壁厚和截面邊長．

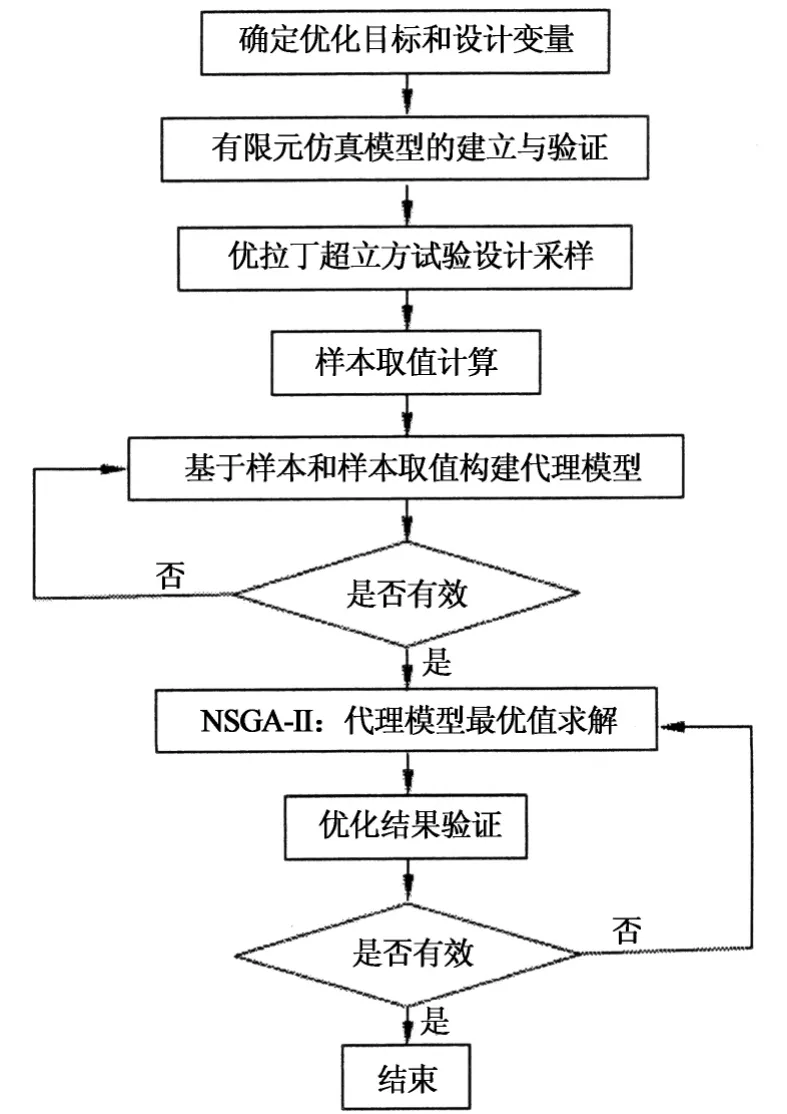
圖10 優化流程圖Fig．10 Optimization process sketch map

平均壓潰力Fav的回歸方程的決定系數R2為99．97%，比吸能SEA的回歸方程的決定系數R2為99．93%，最大壓潰力Fpeak的回歸方程決定系數R2為99．99%．由R2值可以看出，這3個二階多項式響應面模型的擬合精度較好，能夠較好地滿足預測精度的要求．

表3給出了5個隨機樣本點的設計目標響應面模型計算值和有限元分析值．從表中可以看出，響應面模型的計算值與有限元的分析值都相當接近，相對誤差不超過5%，因此，設計目標的響應面模型精度都很高，可以替代有限元模型用于后續的多目標優化設計過程．

4．3 優化結果分析

多目標優化問題最明顯的特征就是不存在唯一的全局最優解，而是存在一個最優解集，稱為Pareto解集或Pareto前沿．基于此解集，設計者可以根據具體問題確定最終優化方案．本文基于響應面模型，采用非支配遺傳算法對回歸方程進行多目標優化求解得到的Pareto前沿如圖11所示．圖中三角形點、圓形點和五角星點所示分別為最大壓潰力、比吸能和平均壓潰力的最優解．由于3個目標之間存在相互制約的矛盾，在此以比吸能為主要目標，兼顧最大壓潰力和平均壓潰力，選取權重分別為0．5，0．3，0．2．本多目標優化問題的最優解如圖11中五邊形點所示，此時設計點取整后d＝30mm，t＝1．0mm．

表3 5個樣本點的近似值和有限元分析值Tab．3 The results of RSM and simulation for five sample points

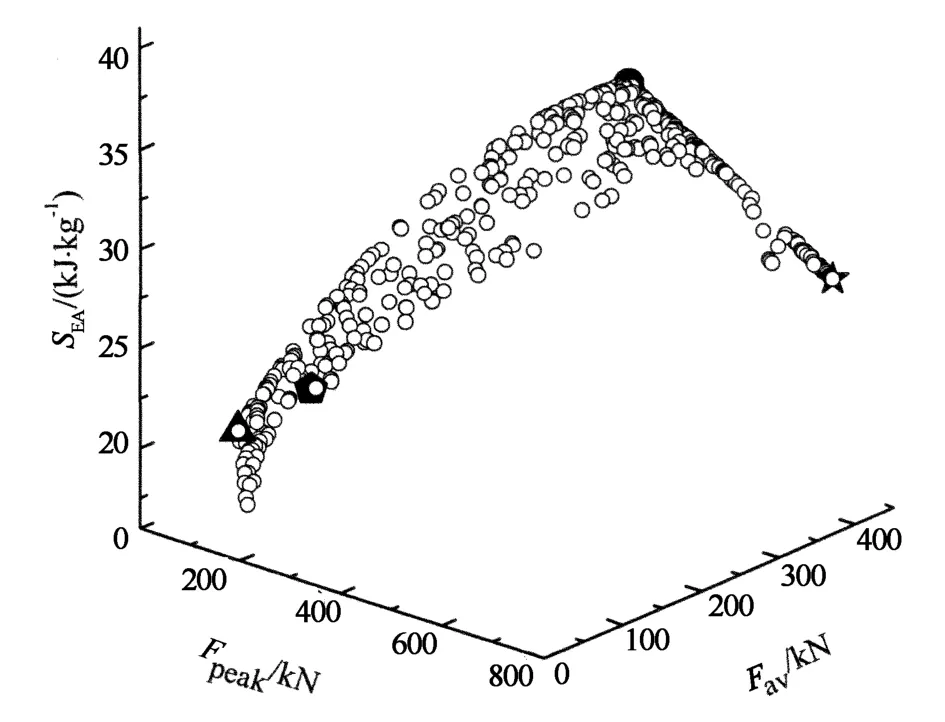
圖11 多目標優化問題的Pareto解集Fig．11 Pareto solution set of multi－objective optimization problem

根據優化結果，考慮到結構的吸能特性以及現有的材料和加工工藝，設計了一種正八邊形多胞管S2S結構，其長度為210mm，截面邊長為30mm，截面形狀如圖5（a）所示，壁厚為1．0mm，并對其進行了有限元仿真，仿真值與優化值的最大相對誤差不超過4%，說明了設計方法具有足夠高的精度．優化設計結果如表4所示，結果表明，多胞管S2S結構的比吸能比優化前提高了33．11%，平均壓潰力提高了6%，最大壓潰力降低了3．78%，優化效果明顯．

表4 優化設計結果對比Tab．4 Comparison between optimization results

5 結 論

研究了一種用于碰撞吸能的正八邊形多胞薄壁管S2S 結構，采用有限元仿真分析了截面形狀（C2C，S2S，C4C 和S4S）和結構參數對吸能特性的影響，并對多胞管S2S 結構的結構參數進行了優化．研究結果表明：

1）與單胞管、多胞管C2C，C4C 和S4S 結構相比，多胞管S2S結構的吸能特性更好；邊對邊布置形式的吸能效果優于角對角布置形式．

2）減小截面尺寸、增加壁厚可以提高多胞管的比吸能，但壁厚的增加使得最大壓潰力也隨之增大；最大壓潰力與壁厚呈近似線性正相關，可以通過減小壁厚和增大截面尺寸降低最大壓潰力．

3）結合優拉丁超立方試驗設計方法和非支配遺傳算法，對多胞管S2S結構的吸能特性進行了優化設計，優化結果比初始設計的吸能特性有了較大提高，比吸能比優化前提高了33．11%，最大壓潰力降低了3．78%，吸能效果更好．

［1］ABRAMOWICZ W，JONES N．Dynamic progressive buckling of circular and square tubes［J］．International Journal of Impact Engineering，1986，4（4）：243－270．

［2］HUANG X，LU G，YU T，etal．On the axial splitting and curling of circular metal tubes［J］．International Journal of Mechanical Sciences，2002，44（11）：2369－2391．

［3］TARIGOPULA V，LANGSETH M，HOPPERSTAD O S，et al．Axial crushing of thin－walled high－strength steel sections［J］．International Journal of Impact Engineering，2006，32（5）：847－882．

［4］顧紅軍，趙國志，陸廷金，等．軸向沖擊下薄壁圓柱殼的屈曲行為的實驗研究［J］．振動與沖擊，2004，23（4）：58－59．

GU Hong－jun，ZHAO Guo－zhi，LU Ting－jin，etal．Buckling of thin－wall cylindrical shell under axial impact［J］．Journal of Vibration and Shock，2004，23（4）：58－59．（In Chinese）

［5］CHEN W，WIERZBICKI T．Relative merits of single－cell，multi－cell and foam－filled thin－walled structures in energy absorption［J］．Thin－Walled Structures，2001，39（4）：287－306．

［6］ZHANG X，CHENG G．A comparative study of energy absorption characteristics of foam－filled and multi－cell square columns［J］．International Journal of Impact Engineering，2007，34（11）：1739－1752．

［7］NAJAFI A，RAIS－ROHANI M．Mechanics of axial plastic collapse in multi－cell，multi－corner crush tubes［J］．Thin－Walled Structures，2011，49（1）：1－12．

［8］亓昌，董方亮，楊姝，等．錐形多胞薄壁管斜向沖擊吸能特性仿真研究［J］．振動與沖擊，2012，31（24）：102－107．

QI Chang，DONG Fang－liang，YANG Shu．Simulation and optimization for blast－resistant performances of a graded aluminum foam sandwich structure［J］．Journal of Vibration and Shock，2012，31（24）：102－107．（In Chinese）

［9］BAI Z，GUO H，JIANG B，etal．A study on the mean crushing strength of hexagonal multi－cell thin－walled structures［J］．Thin－Walled Structures，2014，80：38－45．

［10］JIANG B，ZHU F，JIN X，etal．Computational modeling of the crushing behavior of SKYDEX? material using homogenized material laws［J］．Composite Structures，2013，106：306－316．

［11］ROSSI A，FAWAZ Z，BEHDINAN K．Numerical simulation of the axial collapse of thin－walled polygonal section tubes［J］．Thin－Walled Structures，2005，43（10）：1646－1661．

［12］FAN Z，LU G，LIU K．Quasi－static axial compression of thinwalled tubes with different cross－sectional shapes［J］．Engi－neering Structures，2013，55：80－89．

［13］張宗華，劉樹田．多邊形薄壁管動態軸向沖擊的耐撞性研究［C］／／2007年中國汽車工程學會年會論文集．北京：機械工業出版社，2007：437－443．

ZHANG Zong－hua，LIU Shu－tian．Crashworthiness of dynamical axial crushing of polygonal thin－walled tubes［C］／／2007SAE－China Congress Proceedings．Beijing：China Machine Press，2007：437－443．（In Chinese）

［14］白中浩，陳天志，曹立波，等．基于正交設計的汽車前縱梁吸能結構的優化［J］．汽車工程，2010，32（11）：935－939．

BAI Zhong－hao，CHEN Tian－zhi，CAO Li－bo，etal．Optimization of energy－absorbing structure of vehicle front side rail based on orthogonal design［J］．Automotive Engineering，2010，32（11）：935－939．（In Chinese）

［15］曹立波，崔崇禎，白中浩，等．八邊形逐級吸能梁的設計與優化［J］．湖南大學學報：自然科學版，2010，37（1）：29－34．

CAO Li－bo，CUI Chong－zhen，BAI Zhong－hao，etal．Design and optimization of the octagonal step by step energy［J］．Journal of Hunan University：Natural Sciences，2010，37（1）：29－34．（In Chinese）

［16］JONES N．Energy－absorbing effectiveness factor［J］．International Journal of Impact Engineering，2010，37（6）：754－765．

［17］白中浩，盧靜．基于多目標優化的兒童座椅匹配方法［J］．湖南大學學報：自然科學版，2013，40（3）：52－58．

BAI Zhong－hao，LU Jing．Study of matching for a child seat based on multi－objective optimization［J］．Journal of Hunan University：Natural Sciences，2013，40（3）：52－58．（In Chinese）

［18］YIN H，WEN G，HOU S，etal．Crushing analysis and multiobjective crashworthiness optimization of honeycomb－filled single and bitubular polygonal tubes［J］．Materials and Design，2011，32（8／9）：4449－4460．