計及經濟效益的分布式電源多目標優化規劃＊

譚陽紅，王 偉

（湖南大學 電氣與信息工程學院，湖南 長沙 410082）

分布式發電（Distributed Generator，DG）是一種新興的能源利用方式，其定義可概括為：直接布置在配電網或分布在負荷附近的發電設施，用以經濟、高效、可靠地發電［1－6］．分布式發電系統中的發電設施稱為分布式電源，主要包括風力發電、光伏發電、微型燃氣輪機、燃料電池、小水電等．DG 接入配電網中具有節省投資、降低能耗、提高電力系統的可靠性和靈活性等優點［7－8］．

對于DG 接入配電網的優化問題，一般包括選址和定容兩個方面．若接入位置和容量不當，不僅會增加系統網損，還會增加經濟損失．因此，獲得經濟效益最好的配置方案顯得尤為重要．文獻［9－11］以有功網損最小為單目標進行DG 的優化配置，未考慮經濟效益等因素．文獻［12－16］以最大經濟效益為目標函數建立了優化模型，卻沒有考慮接入DG后對系統運行帶來的影響．文獻［17］僅僅考慮了單一類型的DG 接入配電網，而沒有考慮多種類型的DG 同時加入配電網的情況．文獻［18－19］雖然考慮了多目標優化，但都從兩個角度考慮了其優化問題，使得考慮不夠全面．文獻［20］建立了DG 優化多目標模型，在優化過程中從投資費用、網損、電壓三個角度獨立研究分析了各個目標的作用，但沒能把多目標函數聯系在一起進行綜合研究．文獻［21］深入研究了對獨立微網系統中可控型微電源的組合優化問題，但并未涉及微網并網優化運行問題．

中國是一個能源生產和消費大國，經濟的快速發展導致能源需求的快速增長．為緩解能源資源不足，供應壓力大，環境保護矛盾突出，能源技術落后等問題，實現經濟的快速發展，能源的多樣化和可持續發展，增加可循環能源的開發，是我國現階段的主要任務，也是21世紀電力工業發展的主要方向．所以將經濟效益納入優化配置模型中具有實際意義．基于以上原因，本文提出了綜合考慮經濟效益和有功網損的多目標優化模型，應用量子粒子群算法對不同類型DG 的選址和定容進行優化［22－23］，并通過IEEE33節點系統對所提出的模型和方法進行驗證．

1 分布式發電優化配置指標

以配電網有功損耗費用、分布式電源運行費用和系統有功網損最小作為系統經濟性評價指標，該指標由以下3部分構成．

1．1 配電網有功損耗費用

配電網有功損耗費用為：

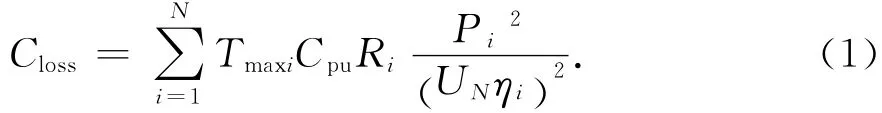
式中：Tmaxi為支路i的一年最大網損時間（h）；Cpu為單位電價（元／kWh）；Pi為流過第i條支路的有功功率；Ri為第i條支路的電阻；ηi為第i條線路上的負荷功率因數；UN為配電網的額定電壓；N為支路總數．

1．2 分布式電源運行費用

分布式電源運行費用為：

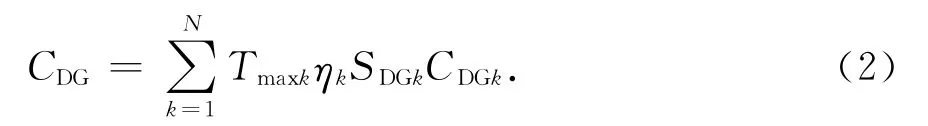
式中：Tmaxk為第k個分布式電源一年內的最多發電時間（h）；ηk為第k個分布式電源的功率因數；SDGk為第k個分布式電源的電機容量；CDGk為第k個分布式電源的單位電量發電耗費（元／kWh）．

1．3 系統有功網損

分布式電源加入配電網會對系統的潮流分布產生重要影響，合理配置DG 的位置和容量，可有效減小支路的潮流流動，從而降低系統的網損．但是，如果DG 的配置不合理，注入功率過高時，反而會增大支路的潮流流動，增加系統的網損．所以，采用系統的有功網損作為指標：

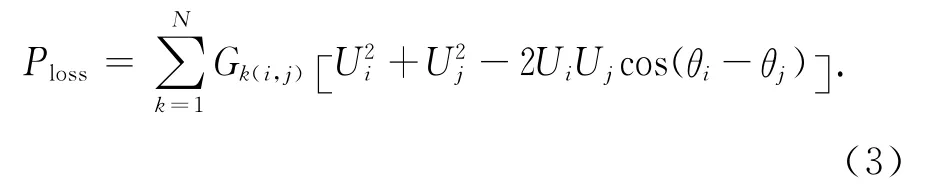
式中：Ploss為系統的有功損耗；N為系統的支路數；Gk（i，j）為第k條支路的電導；i，j分別為支路k兩端的節點編號；Ui和Uj分別為節點i和j的電壓幅值；θi和θj分別為節點i和j的相角差．

2 分布式發電多目標優化配置模型

2．1 目標函數

目標函數為：

式中：F為配電網有功損耗費用、分布式電源運行費用和系統有功網損三者之和；λa，λb，λc分別為多目標權重系數，0＜λa＜1，0＜λb＜1，0＜λc＜1，權重系數可根據實際背景進行適當調整．

2．2 約束條件

約束條件包含等式約束條件和不等式約束條件兩部分．

2．2．1 等式約束

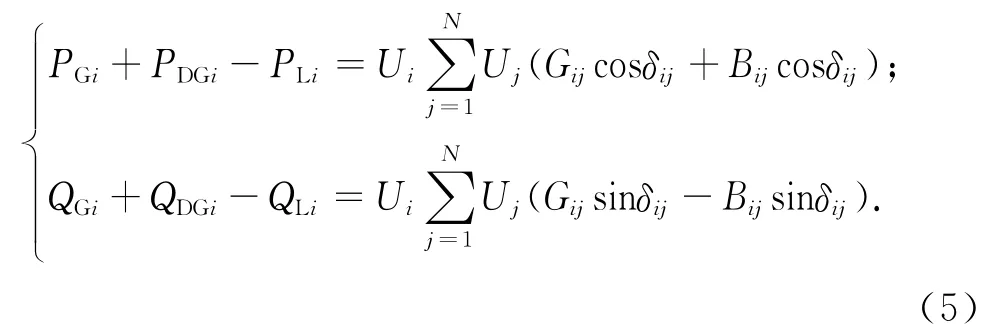
式中：PGi，QGi分別為節點i處發電機的有功、無功出力；PDGi，QDGi分別為節點i處分布式電源的有功、無功功率；PLi，QLi分別為節點i處發電機的有功、無功負荷功率；Ui，Uj分別為支路首末節點處的電壓；δij為節點i，j的相角差值．

2．2．2 不等式約束

1）DG 的總容量約束：

即所有接入的DG 總容量應不大于DG 并網總容量的最大值．自然環境因素對于分布式電源發電有很大的影響，電機的啟動、停機具有隨機性，若分布式電源在配電網中的容量過大，會使得系統的電能質量下降．一些研究表明，通常DG 的總容量不會大于配電網總負荷的1／10．其在優化配置中采用的懲罰函數表達式為：

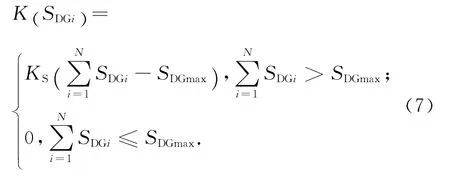
式中：SDGi為所有接入的DG總容量；SDGmax為DG并網總容量的最大上限；KS為DG 總容量越限的懲罰因子，為一個很大的正常數．

2）各節點處的DG 約束容量：

式中：SDGimax為第i個節點處DG 的容量最大值．其懲罰函數為：

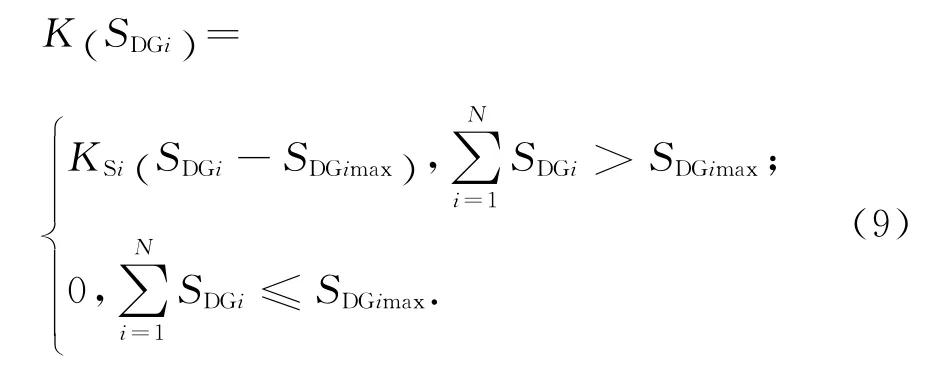
式中：SDGi為接入節點i的DG 的容量大小；KSi為節點i所接入容量越限的懲罰因子，為一個較大的正常數．

3）節點電壓約束：

式中：Uimin，Uimax分別為節點i所允許通過的電壓上下限．其懲罰函數為：

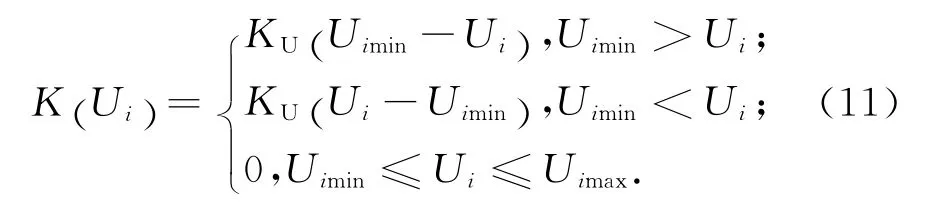
式中：Ui為節點i的電壓；KU為節點電壓在運行極限下偏離的懲罰因子，為一個較大的正常數，當取0時電壓沒有越限．

4）支路電流約束：文中提到的最大載荷電流不能小于支路電流，其懲罰函數如下．

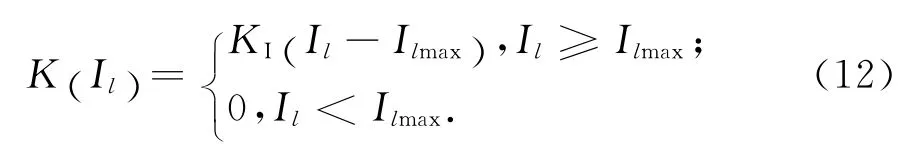
式中：Il為支路l的電流；Ilmax為第l條支路所允許通過的最大電流值；KI為線路電流越限懲罰因子，為一個較大的正常數，當取0時電流沒有越限．

3 DG 優化配置的量子粒子群方法

3．1 量子粒子群算法

粒子群優化（Particle Swarm Optimization，PSO）算法是群體智能優化算法中的一種典型算法，于1995年由美國社會心理學家Kennedy博士和電氣工程師Eberhart博士共同提出［24］．該算法的思想來源于早期對鳥類群體行為的研究，并具有計算簡單、易于實現、控制參數少等特點．在PSO 算法中每一個候選解稱之為一個“粒子”，若干個候選解就組成了鳥的群體．這里的每個粒子沒有重量和體積，通過目標函數來確定它的適應值．在解空間中運動的每個粒子，都是由速度來決定他的運動方向和距離，粒子通過追隨自身的個體最好位置與群體的全局最好位置來動態地調整自己的位置信息．但是隨著時間的推移，粒子的運動軌跡受到一定的影響；同時粒子的速度也受到一定的限制，使粒子的搜索空間受到限制并逐漸減小，不能搜索到整個可行解的空間，容易陷入局部最優解，從而不能保證全局收斂．

針對PSO 算法這一缺點，根據粒子群收斂的基本性質，結合量子力學中的相關理論，從中提出了基于δ勢阱模型的量子行為粒子群優化算法［25］；在此基礎上，為了進一步完善上述算法，針對算法的重要參數即波函數的特征長度的特性，設計了一種新的基于全局水平的參數控制方法，從而更加完善了量子粒子群優化（Quantum Particle Swarm Optimization，QPSO）算法［26］．

3．2 算法流程

在一個N維的目標搜索空間中，QPSO 算法由M個代表潛在問題解的粒子組成群體X（t）＝，在t時刻，第i個粒子位置為：

Xi（t）＝…，M．粒子沒有位置向量，個體最好位置表示為：

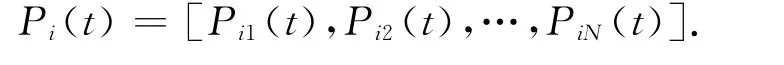
群體的全局最好位置為：

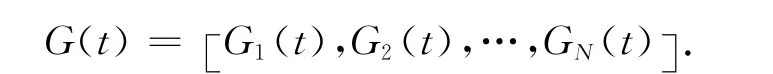
前一次迭代的群體全局最好位置為：

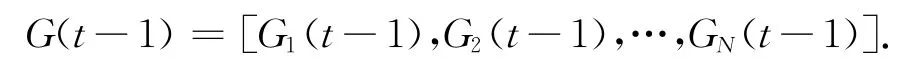
粒子i的個體最好位置pbest由下式確定：

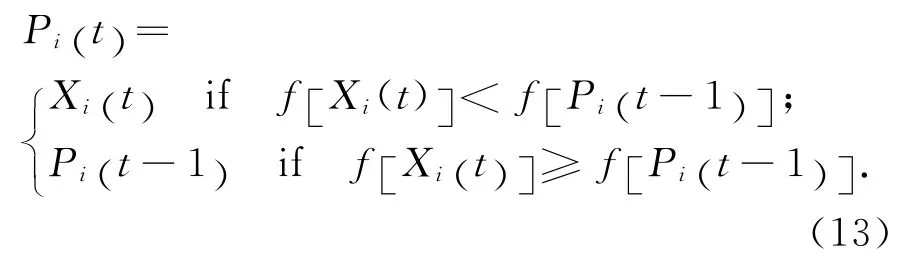
式中：f［Xi（t）］ 代表粒子i當前位置的適應值；f［Pi（t－1）］代表粒子i前一次迭代的適應值．

群體的全局最好位置由式（14）和式（15）確定：

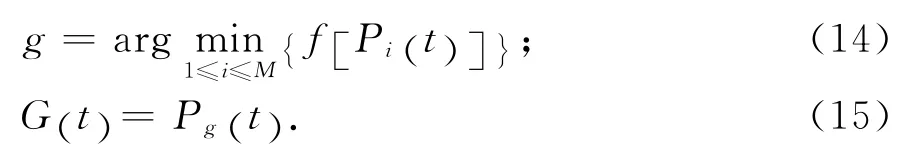
但在實際算法運行中，由于每一次更新粒子位置前都要計算全局最好位置，因此只需將每一個粒子的當前個體位置適應值與全局最好位置的適應值比較，如果前者好，則G（t）更新；否則，G（t）不更新．令

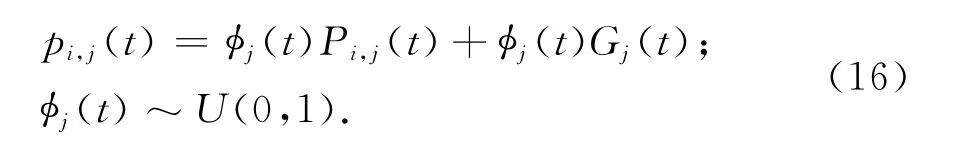
式中：pi，j（t）為粒子i的一個隨機點位置坐標；φj（t）為區間（0，1）上均勻分布的隨機數；Pi，j（t）為粒子i的個體最好位置坐標．則粒子的進化方程為：

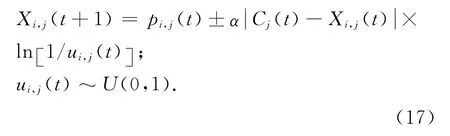
式中：Xi，j（t＋1） 為粒子i的位置坐標．

所有粒子個體平均最好位置為：

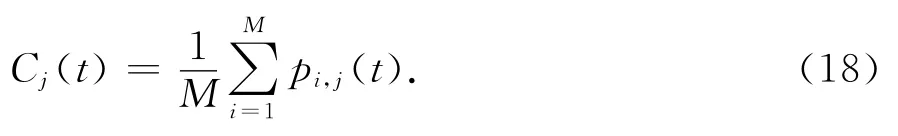
3．3 算法步驟及流程圖

1）置t＝0，在問題空間中初始化粒子群中每一個粒子的當前位置Xi（0），并置個體最好位置Pi（0）＝Xi（0）．

2）根據式（18）計算粒子群的平均最好位置．

3）對于粒子群中的每一個粒子i（1≤i≤M），執行步驟4）－7）．

4）計算粒子i的當前位置Xi（t）適應值，根據式（13）更新粒子的個體最好位置，即將Xi（t）適應值與前一次迭代的適應值比較，如果Xi（t）適應值優于的適應值，即，則置Pi（t）＝Xi（t）；否則，Pi（t）＝Pi（t－1）．

5）對于粒子i，根據式（14），（15）計算群體的全局最好位置，將Pi（t）的適應值與全局最好位置的適應值進行比較，若優于G（t－1） 的適應值，即，則置G（t）＝Pi（t）；否則G（t）＝G（t－1）．

6）對粒子i的每一維，根據式（16）計算得到一個隨機點的位置．

7）根據式（17）計算粒子的新的位置．

8）若達到最大迭代次數或粒子在最大迭代代數內沒有獲得更好值，則滿足算法的終止條件，算法結束；否則置t＝t＋1，返回步驟2）．

基于QPSO 算法的分布式電源多目標優化程序流程如圖1所示．

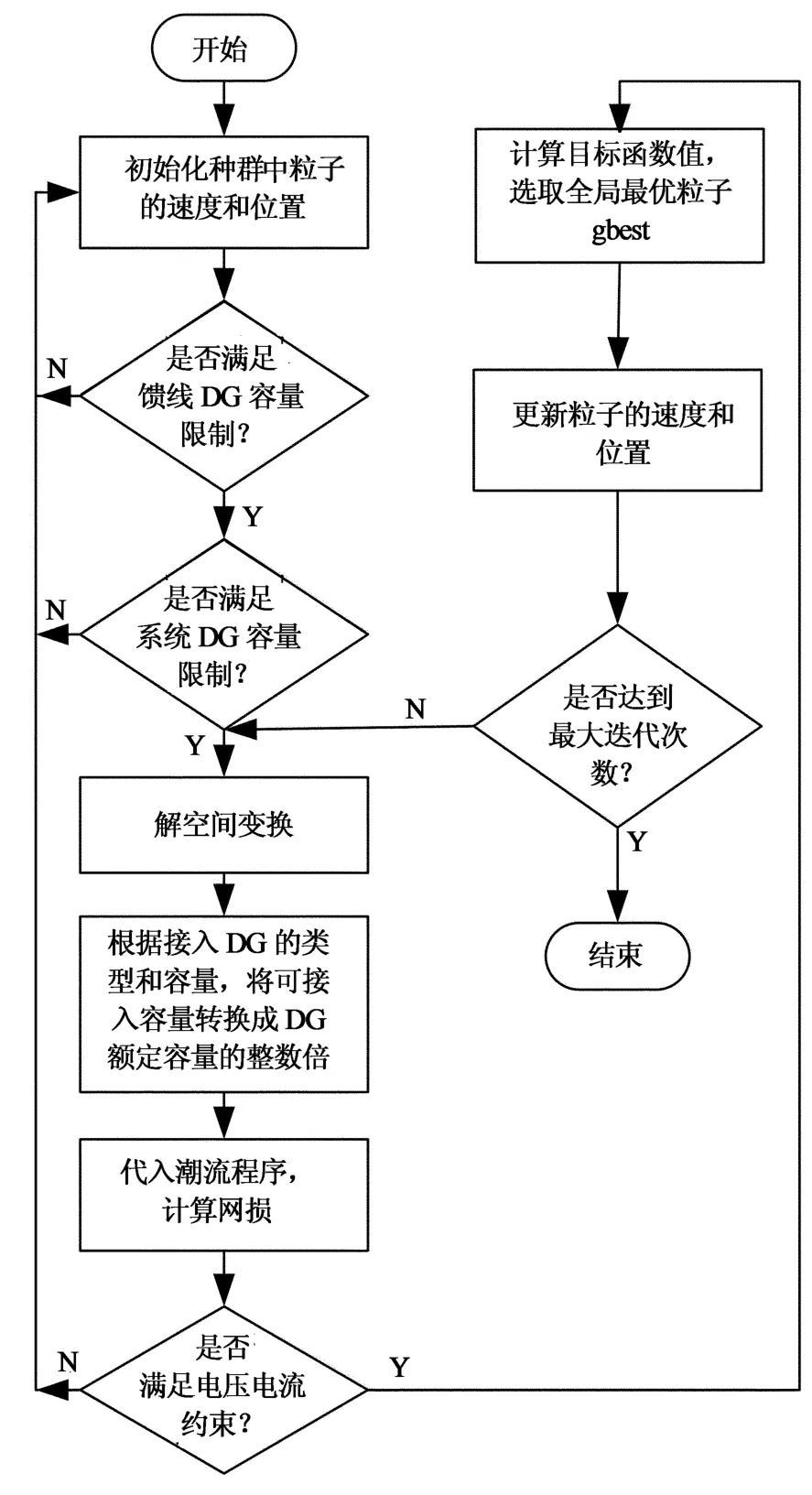
圖1 計及經濟效益的DG 多目標優化配置流程圖Fig．1 DG account the economic benefits of multi－objective optimization configuration flow chart

4 仿真算例與結果分析

4．1 仿真算例

本文采用IEEE33節點的配電系統進行算例分析，如圖2所示，對分布式電源的位置和容量進行優化．該系統包含32條支路、5條聯絡開關，其中節點0為電源節點（平衡節點），系統首端基準電壓為12．66kV，三相功率基準容量為10 MVA，系統總有功負荷為3 715 kW，總無功負荷為2 300kvar．系統的節點負荷和支路阻抗以及參數設置詳見文獻［27］．

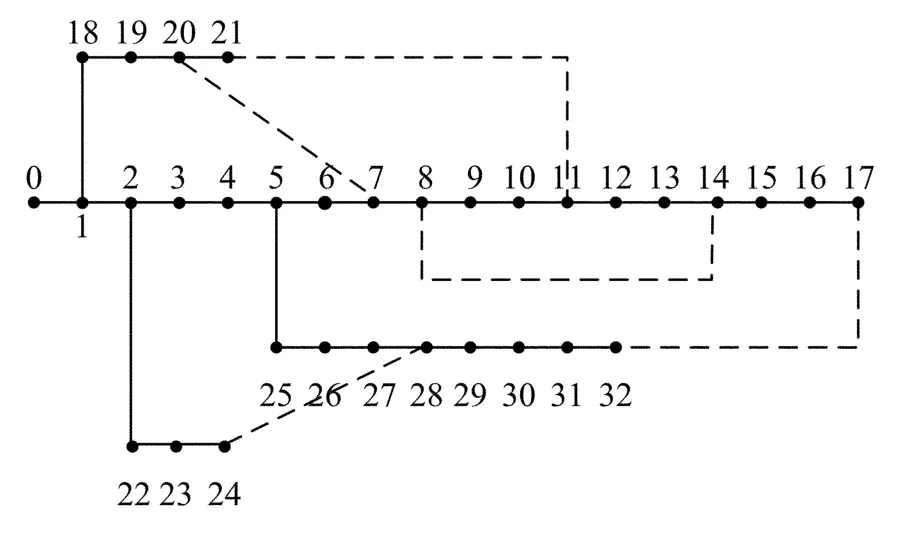
圖2 IEEE33節點配電系統Fig．2 IEEE33node distribution system

采用量子粒子群算法求取最優解時，各參數設為：初始種群規模為50，最大迭代次數為100，收斂精度為1×10－6，邊界變異系數c為0．02；單位配電網損電價Cpu＝0．65元／kWh，每條支路的一年最大網絡損耗時間為8 760h；單獨一個分布式電源的容量為10kW 的整數倍，分布式電源一年的最大發電時間Tmax＝6 000h，不同類型的分布式電源的功率因數、容量范圍和單位發電成本見表1；懲罰因子KS，KSi，KU，KI都設為1 000；權重系數λa＝0．3，λb＝0．3，λc＝0．4．

為了減少搜索范圍，縮短運行時間，經優化后配電網中可以安裝分布式電源的節點有14，17，20，21，24，32．現有4種類型的分布式電源可接入配電網，其類型、功率因數、單位發電成本和容量范圍等參數如表1所示．

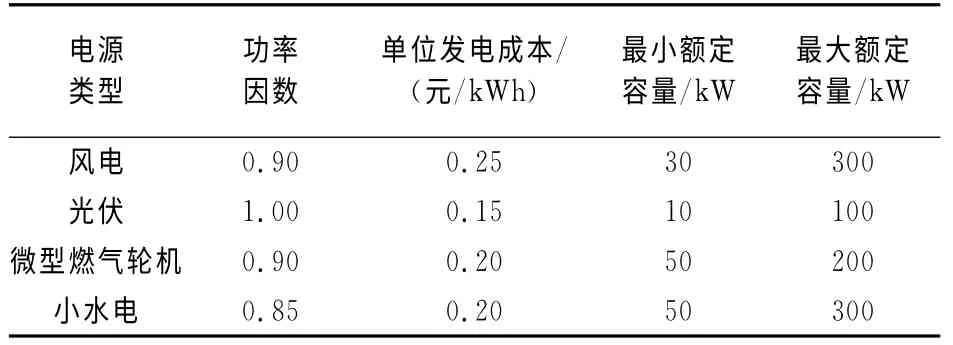
表1 4種分布式電源參數情況Tab．1 Four kinds of distributed power parameters case

配電網中可以接入多種類型的DG，當不同類型、不同容量的DG 接在不同位置的配電網中會產生不同的影響．在優化前未接入DG 時，配電網的有功網損為202．646 3kW，節點最低電壓為0．918 3 pu．優化形式不同的DG 組合，并對其產生的影響結果進行分析．

4．2 含有2種DG 組合的情況

方案1：風電、光伏組合．當把風電、光伏同時加入上述區域，經優化后，系統有功損耗為62．600 9 kW，有功損耗降低率為69．11%，節點最低電壓為0．956 1pu，總費用為2．149 2×105元．DG 接入位置及容量如表2所示．

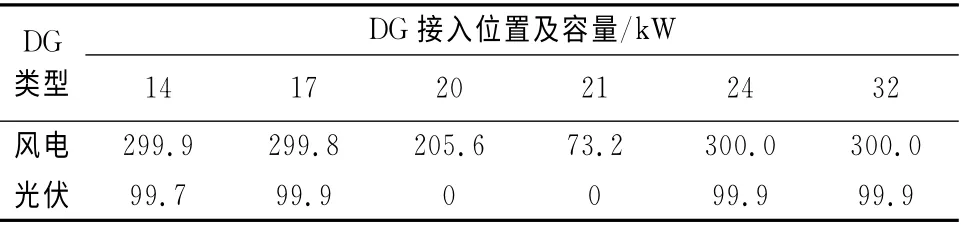
表2 方案1的DG 安裝位置與容量Tab．2 One program installation location and capacity of DG

方案2：風電、微型燃氣輪機組合．當把風電、微型燃氣輪機同時加入上述區域，經優化后，系統有功損耗為45．594 8kW，有功損耗降低率為77．50%，節點最低電壓為0．964 9pu，總費用為1．569 6×105元．DG 接入位置及容量如表3所示．

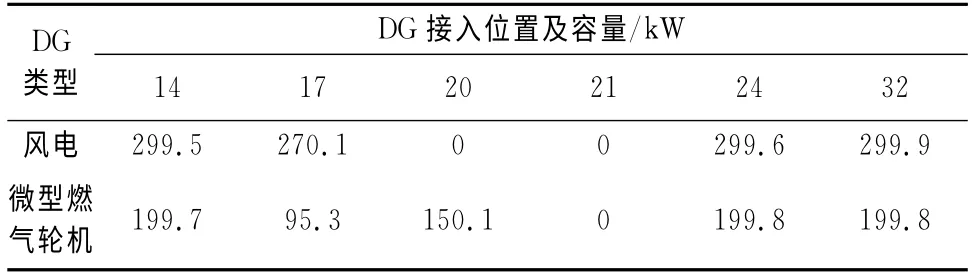
表3 方案2的DG 安裝位置與容量Tab．3 Two program installation location and capacity of DG

方案3：風電、小水電組合．當把風電、小水電同時加入上述區域，經優化后，系統有功損耗為35．208 2kW，有功損耗降低率為82．63%，節點最低電壓為0．970 8pu，總費用為1．215 5×105元．DG 接入位置及容量如表4所示．

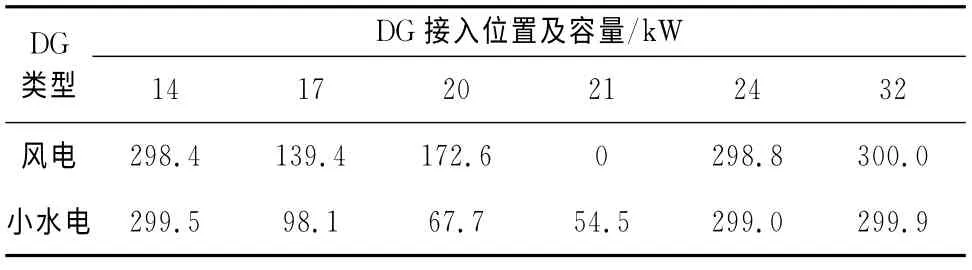
表4 方案3的DG 安裝位置與容量Tab．4 Three program installation location and capacity of DG

本文將量子粒子群算法應用到配電網經濟優化中進行分析，計算結果得出的不同方案下配電網節點電壓幅值如圖3所示，總費用收斂特性曲線如圖4所示．

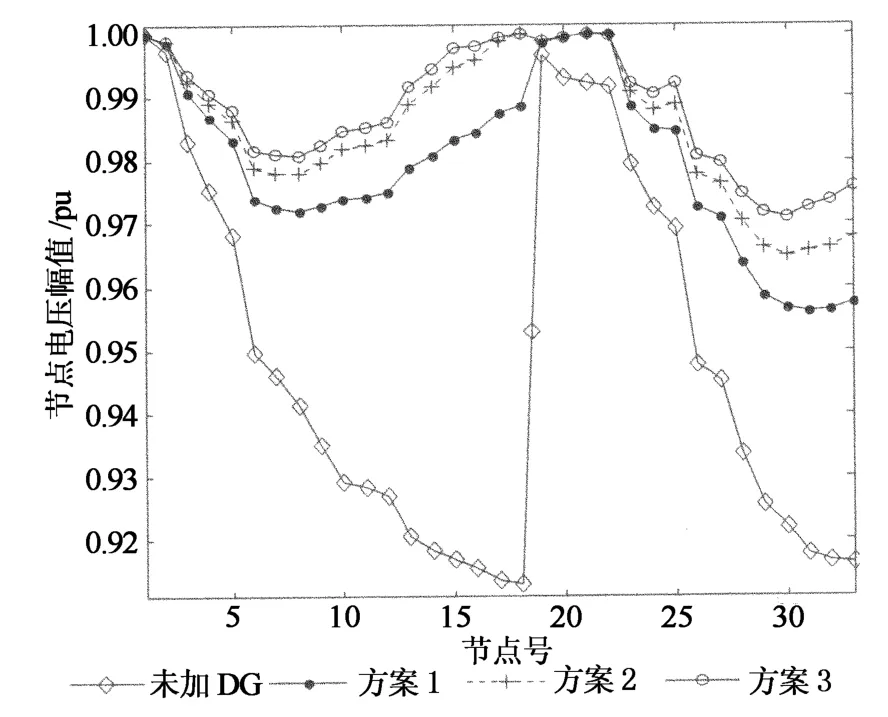
圖3 接入2種類型DG優化前后的系統節點電壓幅值Fig．3 System access node voltage amplitude before and after optimization are two types DG

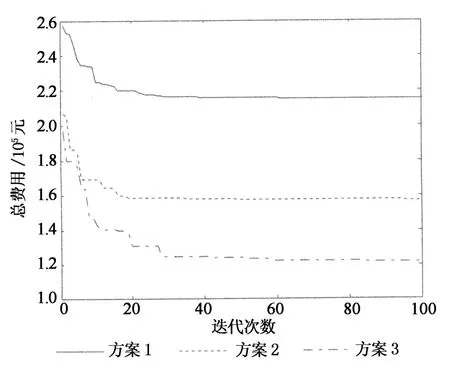
圖4 方案1，2和3經濟費用的收斂特性曲線Fig．4 Option one，two，three economic cost curve

由圖3和圖4可以看出，本文算法能有效地進行2種類型DG 的優化配置問題．當系統接入DG后，系統的各節點電壓較初始網絡均有所提高．方案1在50代左右進入收斂，方案2在20代左右，方案3在30代左右，算法的收斂性較好．

4．3 含有3種DG 組合的情況

方案4：風電、光伏、微型燃氣輪機組合．當把風電、光伏、微型燃氣輪機同時加入上述區域，經優化后，系統有功損耗為41．376 8kW，有功損耗降低率為79．58%，節點最低電壓為0．968 5pu，總費用為1．426 3×105元．DG 接入位置及容量如表5所示．

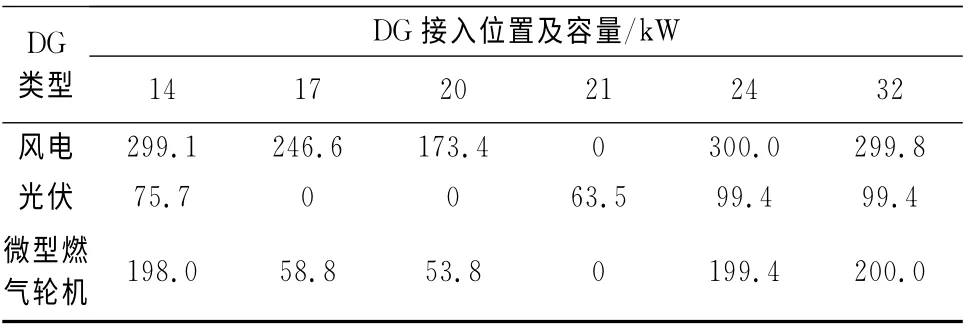
表5 方案4的DG 安裝位置與容量Tab．5 Four program installation location and capacity of DG

方案5：風電、光伏、小水電組合．當把風電、光伏、小水電同時加入上述區域，經優化后，系統有功損耗為32．700 0kW，有功損耗降低率為83．86%，節點最低電壓為0．974 2pu，總費用為1．129 9×105元．DG 接入位置及容量如表6所示．

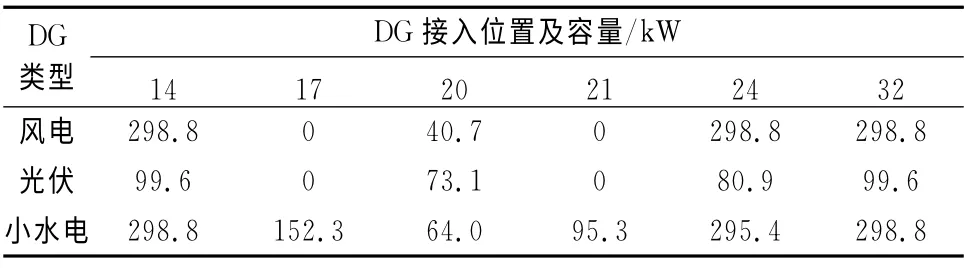
表6 方案5的DG 安裝位置與容量Tab．6 Five program installation location and capacity of DG

方案6：風電、微型燃氣輪機、小水電組合．當把風電、微型燃氣輪機、小水電同時加入上述區域，經優化后，系統有功損耗為27．365 0kW，有功損耗降低率為86．50%，節點最低電壓為0．978 4pu，總費用為9．487 3×104元．DG 接入位置及容量如表7所示．

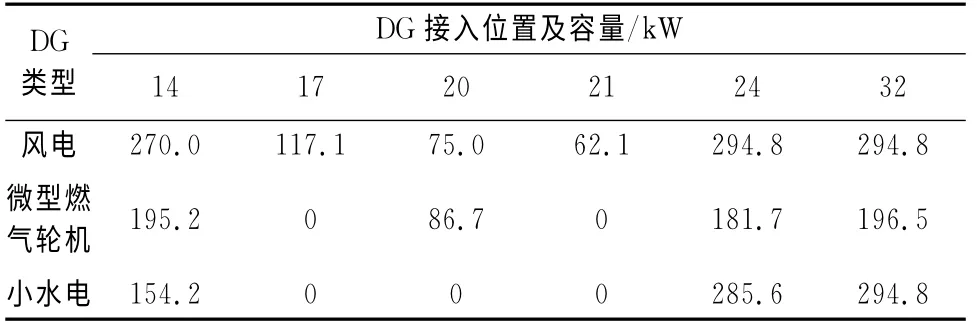
表7 方案6的DG 安裝位置與容量Tab．7 Six program installation location and capacity of DG

由圖5和圖6可以看出，本文算法也能有效地進行3種類型DG 的優化配置問題．當系統接入DG后，系統的各節點電壓較初始網絡均有所提高．方案4在40代左右進入收斂，方案5在50代左右，方案6在70代左右，算法的收斂性較好．

4．4 各種接入方案比較

從上述優化方案結果可以看出，若只考慮有功網損，則使有功網損最小的是方案6：風電、微型燃氣輪機、小水電組合．當計及DG 運行費用時，由于權重系數對網損的影響較大，因而一般情況下總耗費會跟隨有功網損的變小而降低，所以總耗費最小的組合也是方案6．相反，總耗費最大的是方案1：風電、光伏組合．運行成本費用的不同源自于不同類型的DG 組合，因此，我們在抽取被優化后的結果時，首先應該從目標類型組合的角度考慮問題，不一樣的優化結果對應著不同的組合目標．總的來說，以上被優化的DG 對有功網損的減少起到了一定的作用，與此同時對于改進負荷節點電壓，使其在靜態電壓方面的穩定性、電能質量以及一部分線路的負載能力方面得到了極大的改善．

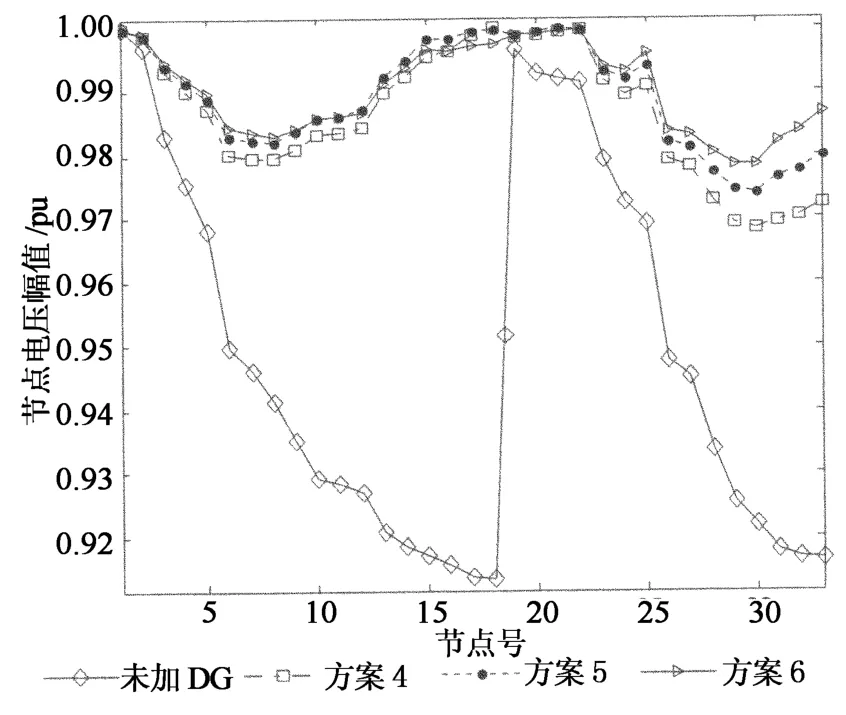
圖5 接入3種類型DG優化前后的系統節點電壓幅值Fig．5 System access node voltage amplitude before and after optimization are three types DG

圖6 方案4，5，6經濟費用的收斂特性曲線Fig．6 Option four，five，six economic cost curve

5 結 論

本文在綜合考慮經濟運行成本和系統有功損耗最小的情況下，研究了配電網中分布式電源的位置和容量優化問題，對所研究過程及結果總結如下：

1）本文以配電網有功損耗費用、分布式電源運行費用及系統有功網損3個指標最小為目標函數，進行了含DG 優化選址問題建模，并對每個子目標函數設置權重，使優化結果更加靈活可靠．

2）選取風電、光伏、微型燃氣輪機、小水電這4種典型的DG 進行優化，由于不同類型的DG 其運行機理不同，所以優化后DG 的最優輸出容量和位置也不同，使得規劃更加貼合實際，更有利于方案的選取．

3）采用量子粒子群算法解決分布式電源多目標優化，并能對約束條件進行更加靈活的處理．

算例分析表明：將經濟效益和有功網損綜合納入優化模型中，能夠更加全面地評估DG 的優勢，提高電力系統運行水平，節省費用．

［1］JIAYI H，CHUANWEN J，RONG X．A review on distributed energy resources and MicroGrid［J］．Renewable and Sustainable Energy Reviews，2008，12（9）：2472－2483．

［2］AKOREDE M F，HIZAM H，POURESMAEIL E．Distributed energy resources and benefits to the environment［J］．Renewable and Sustainable Energy Reviews，2010，14（2）：724－734．

［3］AL－HAJRI M F，EL－HAWARY M E．Improving the voltage profiles of distribution networks using multiple distribution generation sources［C］／／Power Engineering，2007Large Engineering Systems Conference on．IEEE，2007：295－299．

［4］RAHMAN T K A，RAHIM S R A，MUSIRIN I．Optimal allocation and sizing of embedded generators［C］／／Power and Energy Conference，2004，PECon 2004．IEEE，2004：288－294．

［5］梁有偉，胡志堅，陳允平．分布式發電及其在電力系統中的應用研究綜述［J］．電網技術，2003，27（12）：71－75．

LIANG You－wei，HU Zhi－jian，CHEN Yun－ping．A survey of distributed generation and its application in power system［J］．Power System Technology，2003，27（12）：71－75．（In Chinese）

［6］楊旭英，段建東，楊文宇，等．含分布式發電的配電網潮流計算［J］．電網技術，2009，33（18）：140－143．

YANG Xu－ying，DUAN Jian－dong，YANG Wen－yu，etal．Power flow calculation based on power losses sensitivity for distribution system with distributed generation［J］．Power System Technology，2009，33（18）：140－143．（In Chinese）

［7］HEPBASLI A．A key review on exergetic analysis and assessment of renewable energy resources for a sustainable future［J］．Renewable and Sustainable Energy Reviews，2008，12（3）：593－661．

［8］BAYOD－RùJULA A A．Future development of the electricity systems with distributed generation［J］．Energy，2009，34（3）：377－383．

［9］NARA K，HAYASHI Y，IKEDA K，etal．Application of tabu search to optimalplacement of distributed generators［C］／／Power Engineering Society Winter Meeting．IEEE，2001，2：918－923．

［10］WANG C，NEHRIR M H．Analytical approaches for optimal placement of distributed generation sources in power systems［J］．Power Systems，IEEE Transactions on，2004，19（4）：2068－2076．

［11］ACHARYA N，MAHAT P，MITHULANANTHAN N．An analytical approach for DG allocation in primary distribution network［J］．International Journal of Electrical Power ＆Energy Systems，2006，28（10）：669－678．

［12］TAUTIVA C，CADENA A，RODRIGUEZ F．Optimal placement of distributed generation on distribution networks［C］／／Universities Power Engineering Conference（UP－EC），2009 Proceedings of the 44th Int－ernational．IEEE，2009：1－5．

［13］EL－KHATTAM W，BHATTACHARYA K，HEGAZY Y，et al．Optimal investment planningfor distributed generation in a competitive electricity market［J］．Power Systems，IEEE Transactions on，2004，19（3）：1674－1684．

［14］EL－KHATTAM W，HEGAZY Y G，SALAMA M M A．An integrated distributed generation optimization model for distribution system planning［J］．Power Systems，IEEE Transactions on，2005，20（2）：1158－1165．

［15］SOROUDI A，EHSAN M．A distribution network expansion planning model considering distributed generation options and techoeconomical issues［J］．Energy，2010，35（8）：3364－3374．

［16］JAIN N，SINGH S N，SRIVASTAVA S C．Planning and impact evaluation of distributed generators in Indian context using multi－objective particle swarm optimization［C］／／Power and Energy Society General Meeting．IEEE，2011：1－8．

［17］SINGH D，SINGH D，VERMA K S．GA based optimal sizing＆placement of distributed generation for loss minimization［J］．International Journal of Electrical and Computer Engineering，2007，2（8）：556－562．

［18］MACIEL R S，ROSA M，MIRANDA V，etal．Multi－objective evolutionary particle swarm optimization in the assessment of the impact of distributed generation［J］．Electric Power Systems Research，2012，89：100－108．

［19］ALARCON－RODRIGUEZ A，HAESEN E，AULT G，etal．Multiobjective planning framework for stochastic and control－lable distributed energy resources［J］．IET Renewable Power Generation，2009，3（2）：227－238．

［20］栗然，馬慧卓，祝晉堯，等．分布式電源接入配電網多目標優化規劃［J］．電力自動化設備，2014，34（1）：6－13．

LI Ran，MA Hui－zhuo，ZHU Jin－yao，etal．Multiobjective optimization for DG integration into distribution system［J］．Electric Power Automation Equipment，2014，34（1）：6－13．（In Chinese）

［21］李鵬，李濤，張雙樂，等．基于混沌二進制粒子群算法的獨立微網系統的微電源組合優化［J］．電力自動化設備，2013，33（12）：33－38．

LI Peng，LI Tao，ZHANG Shuang－le，etal．Combinatorial optimization of microsources in standalone microgrid based on chaotic binary particle swarm optimization algorithm ［J］．Electric Power Automation Equipment，2013，33（12）：33－38．（In Chinese）

［22］文升，顧潔，程浩忠，等．分布式電源的準入容量與優化布置的實用方法［J］．電力自動化設備，2012，32（10）：109－114．

WEN Sheng，GU Jie，CHENG Hao－zhong，etal．Maximum penetration level and optimal placement of distributed generation［J］．Electric Power Automation Equipment，2012，32（10）：109－114．（In Chinese）

［23］王成山，陳愷，謝瑩華，等．配電網擴張規劃中分布式電源的選址和定容［J］．電力系統自動化，2006，30（3）：38－43．

WANG Cheng－shan，CHEN Kai，XIE Ying－hua，etal．Siting and sizing of distributed generation in distribution network expansion planning［J］．Automation of Electric Power Systems，2006，30（3）：38－43．（In Chinese）

［24］KENNEDY J，EBERHART R．Particle swarm optimization［C］／／Neural Networks，1995．Proceedings，IEEE International Conference on．IEEE，1995，4：1942－1948．

［25］SUN J，FENG B，XU W．Particle swarm optimization with particles having quantum behavior［C］／／Congress on Evolutionary Computation．2004：326－331．

［26］SUN J，XU W B，FENG B，A global search strategy of quantumbehaved particle swarm optimization［C］／／Proceedings of IEEE Conference on Cybernetics and Intelligent Systems．Singapore，2004：111－116．

［27］劉健，畢鵬翔，董海鵬．復雜配電網簡化分析與優化［M］．北京：中國電力出版社，2002：113－115．

LIU Jian，BI Peng－xiang，DONG Hai－peng．Simplify complex distribution network analysis and optimization［M］．Beijing：China Electric Power Press，2002：113－115．（In Chinese）