飛機缺件停飛與出動能力關系研究

段 剛，劉臣宇，俞金松 （海軍航空工程學院，山東 青島266041）

DUAN Gang, LIU Chen-yu, YU Jin-song (Naval Aeronautical Engineering Institute, Qingdao 266041, China)

0 引 言

按照慣例，飛機缺件停飛率通常用來衡量航材保障的效能。但缺件停飛率作為衡量供應保障效率的管理指標其有效性已日益引起人們的研究興趣。有觀點認為，缺件停飛率高，飛機出動能力就低，兩者之間存在一種線性負相關的關系。據此就可以將飛機的缺件停飛率作為衡量飛機出動能力的一項重要指標。這是一種沒有進行定量分析的結論，不具備科學性。在航材不到位的情況下，機務人員通過串件拼修，可以保證飛機的出動能力不受影響。因此，定量分析缺件停飛與出動能力的關系有一定的研究和應用價值。如果能在缺件停飛與飛機出動能力之間建立某種關系的話，則在評估飛行單位完成其所分配任務的能力時，缺件停飛率應是有用的工具。缺件停飛率與出動能力之間任一關系的存在是選用適當的統計方法檢驗的。為了衡量缺件停飛率對飛機出動能力的影響，采用統計的因缺件停飛而取消的飛行任務數據，并以此作為衡量影響飛行的最佳方法。在其它所有因素保持不變的情況下，衡量缺件停飛率對飛機出動能力的影響程度，其唯一正確的指標是計算確定因缺件停飛的情況取消了多少次飛行任務。

1 缺件停飛率

當一架飛機因缺少備件而不能完成飛行計劃中的任何一項時，該機就屬于缺件停飛。一個機種的缺件停飛率定義為，在規定的期限內累計的缺件停飛時數除以同期內飛機占有的總時數，這一比值就是缺件停飛率。如某機場全月停放s架J型機，則一月份占用總時數z=s（）J×31×24，期間a架J型機缺件停飛n天，本月中s架J型機缺件停飛時數q=a×n×24。因此，一月份缺件停飛率為an/31s。

影響缺件停飛率的因素有：機場修理能力；庫存量管理；串件拼修規定；飛行計劃的重要性；飛機的壽命；對申請器材的積極供應；缺件停飛報告的缺陷；送修器材待收修復品的管理；備件供應與維修部門協作配合；調用緊急配套器材等。

現實中單純以缺件停飛率這一指標，去衡量航材保障效果是不準確的。因此，一個機場某一缺件停飛率，可能不等于另一機場同一缺件停飛率。但若在缺件停飛率與飛機出動能力之間建立某種關系，則在評估一個機場完成飛行任務的能力時，缺件停飛率可作為可靠參數。初步分析認為，在其他因素保持不變的條件下，衡量缺件停飛率對飛機出動能力的影響程度，其唯一正確的指標是計算確定因缺件停飛的情況取消了多少次飛行任務。

2 模型分析

選定的各機場缺件停飛率分別與各自的同期缺件取消飛行任務率相比較，并分析有何關系。同時，各個機型的缺件停飛率分別與各自的缺件取消飛行任務率相比較，以確定在整個機型內它們是否存在一種關系。利用散點圖可便于識別模型，如線性模型、雙曲線形、冪函數模型、指數型等，簡化了選擇合適回歸模型的工作。實例如下：該例的數據（如表1 所示） 顯示了一種線性關系，再輔以相關分析和回歸分析。設定數據散點圖如圖1 所示。

表1 設定數據（某機場某型飛機）

挑選回歸模型方程：

線性方程：Y=A+Bx

二次方程：Y=A+Bx2

為了確信在問題變量之間存在強的線性關系挑選r2=0.8 作為相關重要性的衡量指標。若r2大于或等于0.8，管理人員就能運用缺件停飛率十分準確地預測取消飛行任務數。任何小于0.8 的r2值預測取消任務數就沒有多大價值。在這種情況下，用其他預測方法，如果取平均值，可能得出更好的結果。

3 引入數據

線性模型檢驗數據結果：線性模型r2=1，非線性模型r2=0.9398；非線性模型檢驗數據結果：線性模型r2=0.9404，非線性模型r2=1。

表2～表5 按不同情況整理，提出相關系數平方值匯總情況。

表2 不同機場兩種機型的r2

從表2～表5 看出，無論怎樣分類進行分析，所有r2值都明顯低于所指定的指標值0.8。

4 數據分析

第一個分析結果是，當所有其他因素不變時，缺件停飛率與飛機出動能力之間不是密切相關的。飛機缺件停飛率增加或減小一個量，不會獨自對飛機出動能力造成有利或不利的影響。

第二個分析結果是，對各類機種進行比較，可以看出相應的缺件停飛率與缺件取消飛行任務率的關系是有很大區別的。由此可以推斷一種可能性，即：單一考慮確實存在一定的相關性，但只有將機種作為整體考慮時這種關系才顯得稍微密切。

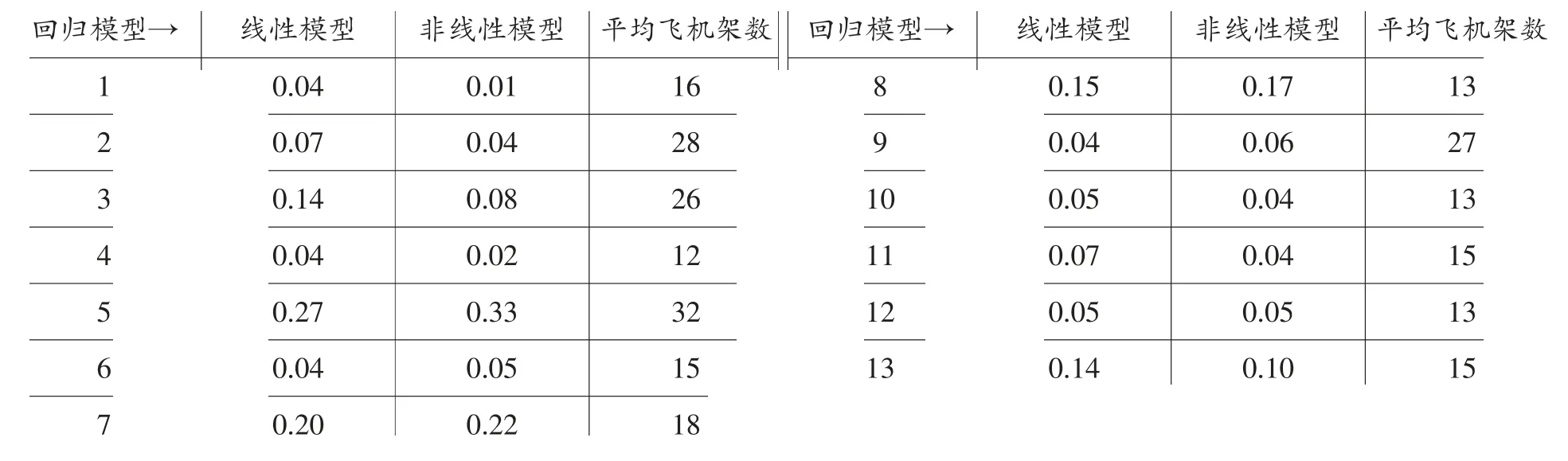
表3 不同機場某種機型的r2

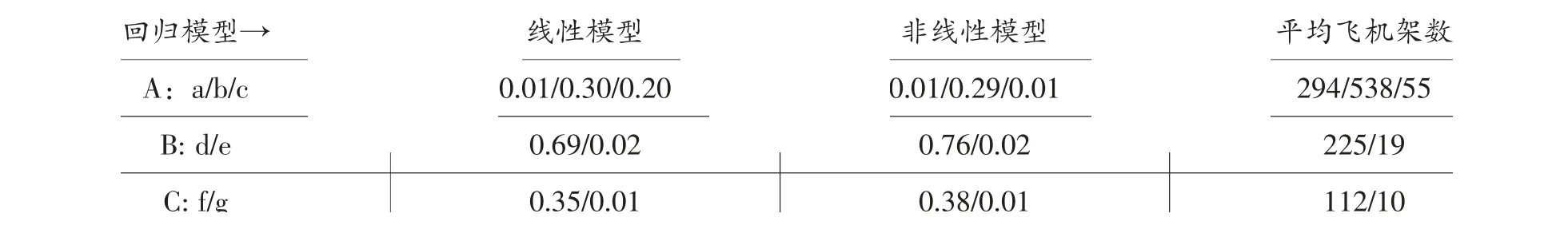
表4 按機場和機種的r2

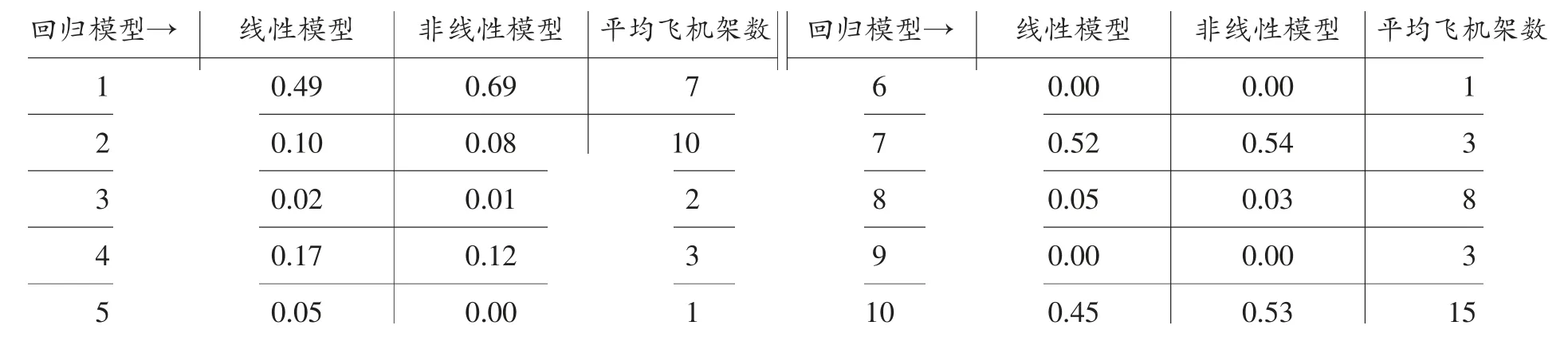
表5 飛機平均架數的r2

第三個分析結果是，當所研究的飛機數量變化時，用缺件停飛率預測飛機出動能力，效果不好。由此斷定缺件停飛率與飛機出動能力之間的關系不受裝備飛機數量的影響。

根據分析結果，第一條建議是，將數據資料擴展到更長的時間范圍，這樣才能完成缺件停飛率與缺件取消飛行任務相關性的分析。由于本文引用數據涉及時間范圍相對較短，因此回歸方程受到散點圖中少數極端點數據的影響。例如，18 個月中一極端數據點有可能使r2從一個重要值（r2≥0.8 ）降低到非重要值（r2≤0.8 ）。為了減輕這種影響，研究表明，3 年的數據就能減弱極端數據點可能出現的影響，并會提供比較準確的結果。

第二條建議，研究中可將串件拼修率和常用器材壽命考慮在內，這兩個變量是影響飛機出動能力的潛在因素。例如，運用關于三個變量的多元線性回歸的標準方法，計算每一個相關的強度和趨勢，然后檢驗各個變量，求出最佳影響因素。研究有助于揭示上述變量的關系，并可清除有關測量值的許多相互矛盾的觀點。

5 結 論

總之，利用缺件停飛率和缺件取消飛行任務率這兩個變量進行線性回歸分析，相關系數r2低于0.8，這表明缺件停飛率和缺件取消飛行任務率之間存在弱相關性。因此，在未更好地研究出兩者之間的實質性關系之前，都不要盲目地把一特定的缺件停飛率與某一具體的飛機出動能力聯系起來。進一步考慮，缺件停飛率作為衡量供應保障率的管理指標應當進行改進，針對不同的機種，重新制定相應的缺件停飛標準。在新的動態缺件停飛保障概念中，可以考慮將機種的壽命、飛行任務的性質和分散形式綜合形成一個數字保障目標，該目標將是新的缺件停飛標準。

[1] 劉臣宇,等. 航材供應[M]. 北京：國防工業出版社，2009:30-31.

[2] 左召軍，鐘新輝. 航材消耗的時間序列分析[J]. 長沙航空職業技術學院學報，2004(3):29-32.

[3] 于倩，干曉蓉. 灰色多元線性回歸分析[J]. 云南師范大學學報，2009,29(3):19-22.

[4] 丁士俊，姜衛平，楊顏梅. 整體最小二乘線性回歸模型與算法[J]. 測繪通報，2012(12):8-10.

[5] 魯鐵定，陶本藻. 基于整體最小二乘法的線性回歸建模和解法[J]. 武漢大學學報（信息科學版），2008,33(5):504-507.

[6] 張志勇，文桂林. 時變時滯系統的灰色預測非線性PID 控制[J]. 系統仿真學報，2009,31(5):44-46.