寬扁型環肋骨圓柱殼強度和穩定性分析
黃加強,陳 杰
(1.海軍駐武漢第七一九研究所軍事代表室,湖北 武漢430064;2.武漢市第二船舶設計研究所,湖北 武漢430064)
0 引 言
加筋圓柱殼作為深潛器的主要耐壓結構,在工程上有著廣泛應用。加筋圓柱殼結構的強度和穩定性一直以來被眾多學者和設計者所關注,也出現了諸多研究成果[1-3]。
傳統水下結構物普遍采用T 型材和球扁鋼等肋骨形式。朱邦俊等[4]對半圓環殼耐壓圓柱殼強度和穩定性進行分析研究,推導了相應的計算公式,并采用實驗方法進行驗證;呂春雷等[5]采用理論分析和數值計算方法對不同型式加筋的圓柱殼穩定性進行對比分析,并給出了關于加強筋設計的建議。為了提高圓柱殼的屈曲承載能力,龍連春等[6]對加筋圓柱殼結構進行優化設計分析,得到了加筋圓柱殼合理的布筋方案。
目前研究的環肋骨結構截面寬度與高度的比值普遍都小于1,但是對于有些深潛器而言,需要對諸多設備進行布置和安裝,由于受到其內部空間的限制,在設計其耐壓結構時,其內部加強筋高度不宜設計過高。為了增加肋骨剛度,只有通過增加肋骨寬度的方式實現,這樣就產生了一類特殊的耐壓結構形式——寬扁型環肋骨加筋圓柱殼,如圖1 所示。本文針對這種特殊的結構形式,采用Ansys 軟件對其強度和穩定性進行計算分析,對比了2 種建模方式下計算結果的差異性,并且與規范值進行比較。同時,通過有限元計算,分析加筋尺寸以及加筋布置方案對結構極限承載能力的影響。
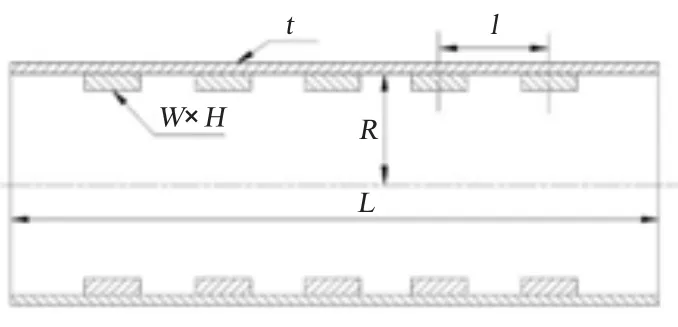
圖1 寬扁型環肋骨加筋圓柱殼結構剖面圖Fig.1 Cross-sectional view ofring-stiffened cylindrical shell withflatribs
1 寬扁型肋骨加筋圓柱殼強度有限元分析
內加筋圓柱殼幾何模型如圖2 所示。耐壓圓柱殼半徑R = 190 mm,耐壓殼板厚t = 7 mm,肋骨間距l = 220 mm,寬扁梁截面尺寸為40 ×18 mm。材料為鋁合金,彈性模量E = 6.9 ×104MPa,泊松比μ =0.32,屈服強度σs= 380 MPa,工作壓強P = 4 MPa。

圖2 典型寬扁梁加筋圓柱殼幾何模型Fig.2 Typical geometry of stiffened cylindrical shellwith flat ribs
采用有限元通用軟件Ansys 進行有限元建模分析。傳統的加筋圓柱殼一般采用殼單元和梁單元進行模擬,由于寬扁型環肋骨加筋圓柱殼具有一定的特殊性,本文將采用2 種不同方法進行模擬計算:1)全部采用體單元;2)圓柱殼采用殼單元,加強筋采用梁單元。將這2 種模擬方法的計算結果進行對比分析,同時與規范計算值進行比較。
1.1 寬扁型環肋骨加筋圓柱殼強度有限元計算
Ansys 軟件中體建模采用solid45 單元模擬;殼、梁單元建模中殼采用shell63 單元,梁采用beam188單元。網格大小保證兩者在周向份數和每個肋距內份數相同。
規范校核中3 個典型位置處的應力分布云圖如圖3 ~圖5 所示。

圖3 相鄰肋骨跨中殼板中面周向應力分布云圖Fig.3 Circumferential stress contours of the middle layer between adjacent ribs

圖4 肋骨跨端殼板內表面縱向應力分布云圖Fig.4 Longitudinal stress contours of bottom layer on cross ribs

圖5 肋骨應力分布云圖Fig.5 Stress contours of the rib
由圖3 可知,殼板在跨中處取得最大周向應力,應力分布規律一致。圖4(a)顯示了體單元內外表面的縱向應力,而圖4(b)顯示為殼單元內表面縱向應力,都表現為肋骨跨端處內表面應力最大,但是體單元最大應力出現在肋骨與殼板截面突變處,而殼單元出現在肋骨中心線處。圖5 顯示兩者應力分布差異很大,體單元肋骨沿厚度方向有應力梯度,而梁單元肋骨為同一應力值。
1.2 寬扁環肋骨加強圓柱殼強度有限元計算與規范計算對比分析
有限元計算值與規范計算值如表1 所示。
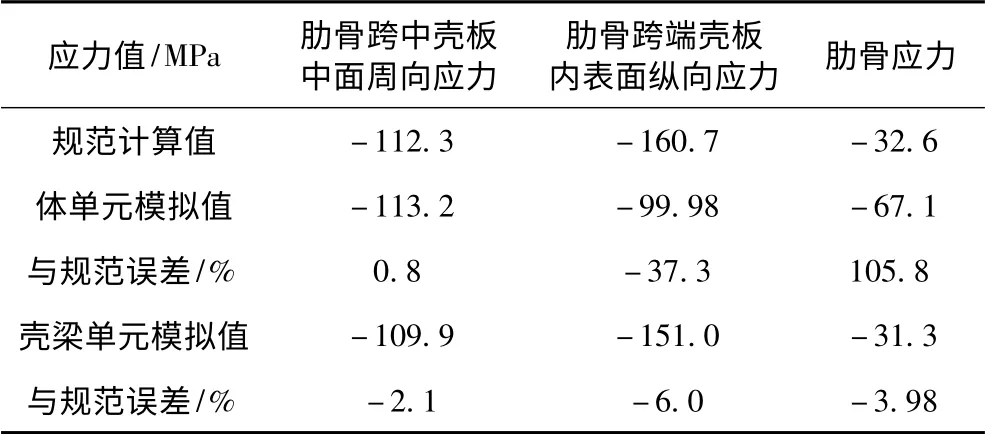
表1 有限元計算與規范計算對比Tab.1 Comparison of calculation between finite element and norm
除肋骨跨中殼板中面周向應力誤差較小外,體單元模擬計算值與規范計算值的差異較大;而殼、梁單元模擬計算值與規范計算值誤差在6%以內,能很好的與規范吻合。
體單元模擬肋骨與殼板共面連接,使得肋骨跨端縱向應力出現在板厚突變處,而不再是肋骨中心線處,這與梁、殼單元模擬有所不同。體單元建模能更準確的反映寬扁梁加強圓柱殼的應力分布。通過對比分析,對于這種特殊的寬扁環肋骨形式,規范中的強度校核部分不再適用。
2 寬扁型肋骨圓柱殼穩定性分析
隨著下潛深度增加,耐壓圓柱殼結構在靜水壓力的作用下會出現屈曲失穩。由于耐壓結構的失穩往往發生在材料的非線性階段[7],因此,關于肋骨加強耐壓圓柱殼穩定性計算,需要同時考慮殼體的幾何非線性(如初始缺陷)和材料非線性的影響。
2.1 寬扁環肋骨加強耐壓圓柱殼穩定性有限元分析
本文采用雙線性材料模型,初始缺陷幅值取耐壓圓柱殼半徑的0.25%。Ansys 軟件中線性屈曲與非線性屈曲的區別在于材料屬性的定義,非線性屈曲需要定義材料屈服強度和材料切線模量(取彈性范圍內楊氏模量1%);施加單位載荷以得到結構特征值屈曲模態,再將屈曲模態以給定的幅值施加到原結構中生成新的有限元模型,形成了以特征值屈曲模態為初始缺陷的非線性屈曲有限元計算模型。
寬扁環肋骨加強圓柱殼的特征值屈曲失穩波形如圖6 所示,圖示為第一階失穩波形(整體失穩)。圖7 和圖8 分別為破壞載荷下的位移分布云圖和位移—載荷曲線圖。

圖6 整體失穩波形Fig.6 Buckling mode

圖7 破壞載荷下位移云圖Fig.7 Shell deformation contourwhen collapsed

圖8 典型位置處位移—載荷曲線Fig.8 Load-displacement curve of theshell
規范中計算結構整體失穩臨界壓力時,考慮了結構的幾何修正和物理修正。有限元計算值與規范計算值見表2。

表2 整體失穩臨界壓力有限元值與規范值對比Tab.2 Comparison of overall instability pressure between finite element and norm
體單元整體失穩臨界壓力較規范計算值偏大,與規范值誤差為22.4%左右,有較大差異。對于本文中的特殊肋骨形式規范中穩定性校核部分不再適用。
3 加筋尺寸及布置方案對結構極限承載能力影響分析
3.1 加筋尺寸對環肋加筋圓柱殼極限承載能力影響分析
對于某些深潛器,由于其內部空間有限,為滿足內部設備安裝等要求,加強筋高度方向的尺寸可能受到限制不能加大,為了提高其極限承載能力,只有增大加強筋的寬度。本節在上節算例的基礎上,將加強筋的寬度作為變量,研究了加強筋寬度對結構極限承載能力的影響。不同加強筋寬度下結構的極限承載能力計算結果見表3。結構的極限載荷與加強筋寬度關系如圖9 所示。

表3 不同加強筋寬度下結構的極限承載能力Tab.3 Ultimatecarrying capacity of structure with different rib width
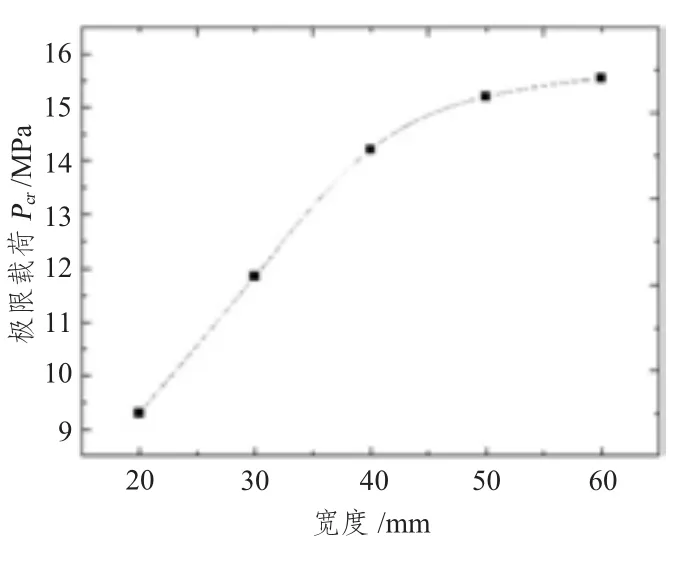
圖9 極限載荷與加強筋寬度關系圖Fig.9 Ultimatecarrying load against rib width
從圖9 可看出,在剛開始階段即加強筋寬度較小時,增大加強筋寬度,能明顯提高結構的極限承載能力,但是隨著肋骨寬度的增加,結構極限承載能力增幅逐漸減小,當肋骨寬度由50 mm 增加到60 mm時,結構極限承載能力提高2.3%,提升空間有限。因此,在結構的設計過程中,要綜合考慮結構的功能性和經濟性,合理地選用加強筋的尺寸。
3.2 加筋布置方案對環肋加筋圓柱殼極限承載能力影響分析
本節在總重量相等的前提下,計算分析3 種加強筋布置方案對加筋圓柱殼極限承載能力的影響,如圖10 所示。
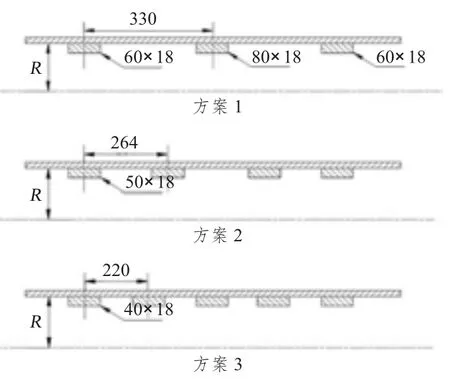
圖10 典型加筋布置方案Fig.10 Typical arrangements of rib
3 種布置方案下加筋圓柱殼的極限承載能力計算結果見表4。

表4 三種布置方案下加筋圓柱殼的極限承載能力Tab.4 Ultimatecarrying capacity of stiffened cylindrical shell with different arrangements
由計算結果可知,3 種方案下加筋圓柱殼極限承載能力基本相當,方案1 相對方案2 和方案3 略微偏大。因此,在此情況下,可根據內部總布置的需求,靈活選用加強筋的設計方案。
4 結 語
通過對具有寬扁型環肋圓柱殼的強度和穩定性進行計算和分析,得到以下結論:
1)對于寬扁型環肋骨圓柱殼這種特殊的結構形式,采用殼、梁單元進行有限元計算已經不再合適,雖然體單元會花費更多的計算代價,卻能準確反映寬扁肋骨耐壓圓柱殼結構的真實應力分布;對比分析結果表明采用規范對此類特殊結構進行強度和穩定性計算,會導致較大誤差。
2)加筋尺寸及布置方案對結構極限承載能力影響分析結果表明,在本文所選用的尺寸范圍內,在加強筋寬度較小時,增大加強筋寬度,能明顯提高結構的極限承載能力,但是隨著肋骨寬度的增加,結構極限承載能力增幅逐漸減小;在總重量相等的前提下,加強筋的3 種布置方案對結構極限承載能力影響不大,因此,可根據內部總布置的需求,靈活選用加強筋的設計方案。
[1]宋保維,成鵬飛,曹永輝,等.藕節形耐壓殼體強度與穩定性有限元分析[J]. 計算機仿真,2007,22(2):54-56.SONG Bao-wei,CHENG Peng-fei,CAO Yong-hui,et al.Strength and stability study of multiple intersecting spheres for pressure hull[J]. Computer Simulation,2007,22(2):54 -56.
[2]黃加強. 長艙段耐壓結構研究進展[J]. 船海工程,2014,43(6):175 -177,181.HUANG Jia-qiang. Research development of the long cabin′s pressure structure[J].Ship & Ocean Engineering,2014,43(6):175 -177,181.
[3]王存福,趙敏,葛彤. 水下耐壓結構拓撲優化設計方法探究[J].工程力學,2015(1):247 -256.WANG Cun-fu,ZHAO Min,GE Tong.Study on the topology optimal design of under water pressure structure[J].Engineering Mechanics,2015(1):247 -256.
[4]朱邦俊,萬正權,徐秉漢,等.半圓環殼型肋骨加強的耐壓圓柱殼結構穩定性研究[J]. 船舶力學,2005(1):79-83.ZHU Bang-jun,WAN Zheng-quan,XU Bing-han,et al. On the buckling of cylindrical shell ring - stiffened by halftubes under hydrostatic pressure[J]. Journal of Ship Mechanics,2005(1):79 -83.
[5]呂春雷,王曉天,姚文,等.多種型式肋骨加強的耐壓圓柱殼體結構穩定性研究[J].船舶力學,2006(5):113-8.LV Chun-lei,WANG Xiao-tian,YAO Wen,et al. Study of buckling of cylindrical shell ring - stiffened by manifold stiffeners under hydrostatic pressure[J]. Journal of Ship Mechanics,2006(5):113 -8.
[6]龍連春,陳興華,傅向榮,等.矩形加筋圓柱殼軸壓屈曲承載力優化[J]. 中國農業大學學報,2009(4):124-130.LONG Lian-chun,CHEN Xing-hua,FU Xiang-rong,et al.Buckling capacity optimization of cylindrical shell with rectangle stiffeners under uniform axial compression[J].Journal of China Agricultural University,2009(4):124-130.
[7]王林.深海耐壓結構型式及穩定性研究[D].北京:中國艦船研究院,2011.WANG Lin. Studies on deep - sea pressure structuraltype and stability [D]. Beijing:China Ship Research &Development Aca de my,2011.

