潛艇水下回轉運動數學模型研究與仿真分析

陳志法，戴余良，鄧 峰，倪 剛

(1.海軍工程大學 動力工程學院，湖北 武漢430033;2.中國人民解放軍92351 部隊，海南 三亞527000)

0 引 言

近些年各國陸續提出了發展海洋經濟、維護海洋權益的戰略方向，海軍的地位日益提高，潛艇作為現代海軍的威懾力量之一，其作用也愈顯重要。為了捕捉戰機、占據有利位置，或者是快速撒離戰場、有效規避反潛武器的攻擊，潛艇水下回轉運動成為一種常用的運動方式，它是潛艇定深直航、變深潛浮和轉向機動等3 種最重要、最基本的運動方式之一［1］，因此有必要對其進行研究。潛艇水下回轉運動時，艇體受力受橫向流影響極大，把潛艇看成一個剛體，利用潛艇重心處的運動參數對其進行求解的傳統方法不再適用，所以本文通過分析對比不同的運動方程，得出合理有效的潛艇水下回轉運動數學模型，采用分段計算方法對潛艇水下回轉運動橫向水動力進行建模仿真，重點分析了潛艇水下定常回轉運動時漂角、回轉角速度、橫傾角以及縱傾角的變化規律，為下一步研究潛艇水下回轉運動非線性特征打下基礎。

1 潛艇水下回轉運動數學模型

研究潛艇水下回轉運動規律，模型是基礎。目前，世界上對潛艇運動模型的研究有很多，1967 年美國泰勒海軍艦船研究與發展中心(DTNSRDC)在進行大量船模試驗和實艇試航的基礎上，發表了“用于潛艇模擬研究的標準運動方程”［2］(本文稱其為67 方程)，因其具有較高權威性而被國際拖曳水池會議(ITTC)所采納，并為廣大研究人員所引用［3］。運用67 方程對潛艇進行研究時，人們把潛艇看成一個剛體，利用潛艇重心處的運動參數對其進行求解，其中海軍工程大學的林俊興等人于2014 年利用此方程對潛艇定常回轉運動的參數變化規律進行了研究［4］。然而1975 年Feldman，J. 在對計算機模擬預報與實艇試驗結果的相關性分析中指出，67方程及其相應的系數在大多數情況下可以對潛艇水下前進運動軌跡做出精確的預報，預報結果與實艇試驗吻合良好，重復性也很好。但是在強機動情況下，如高速、大舵角回轉運動等，其對深度改變、縱傾角和橫傾角的預報需要進一步改進［1］。究其原因，主要是由于潛艇細長型的結構特點，在做高速、大舵角回轉運動等強機動時，潛艇沿艇長方向各點的受力受橫向流影響極大，潛艇運動非線性現象突出。所以，67 方程不能精確地對潛艇水下回轉運動進行模擬仿真。DTNSRDC 于1979 年在67 方程的基礎上又發表了“修正的潛艇標準運動方程”［5］(本文稱其為79 方程)，相比于67 方程，79 方程更多考慮了螺旋槳負荷和航速變化的影響、高速大舵角回轉運動中橫向流突出的問題以及水動力產生的歷程效應，同時它也調整了部分水動力項，使其在理論上能精確地適用于各種復雜環境下潛艇運動軌跡的預報，并且可以準確運用于潛艇運動非線性研究［1］。79 方程對67 方程有很多改進之處［6］，本文結合具體研究工況，分析潛艇水下回轉運動的受力情況發現，橫向水動力是影響回轉運動的主要因素，因此重點分析79 方程與67 方程中橫向力表達式的區別，結果表明，79 方程對部分受橫向流影響的橫向水動力項進行修正，引入橫向流阻力系數Cd，將其從非積分形式改為積分形式，如表1 所示。

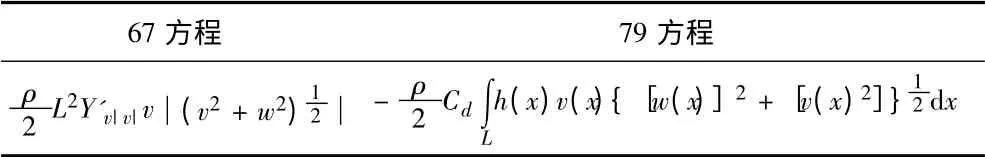
表1 橫向力方程水動力項的變化Tab.1 The variation of the hydrodynamic item in the yawing force equation

其中:h(x)是艇體在xoz 平面內、艇長x 處的局部的高度，v(x)=v +xr 和w(x)=w -xl 分別為此點在z，y 方向的速度分量。

本文采用的潛艇運動方程以79 方程為基礎，針對水下回轉運動工況，參照文獻［7 -8］所述模型，充分考慮潛艇水下回轉運動時橫向流的影響，同時省略影響較小的項，得到具體表達形式如下:

1)軸向力方程

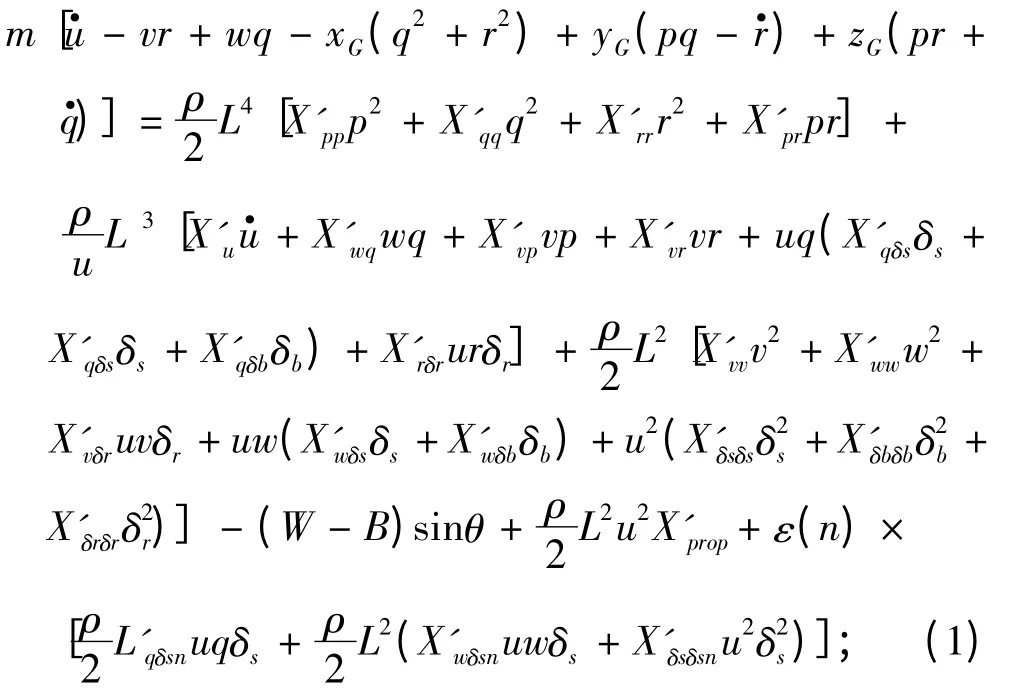
橫向力方程:

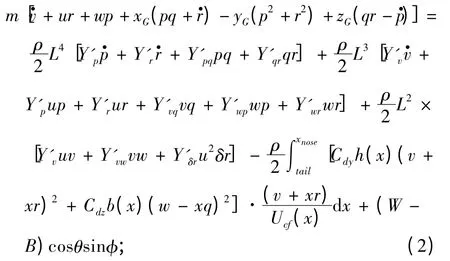
2)垂向力方程

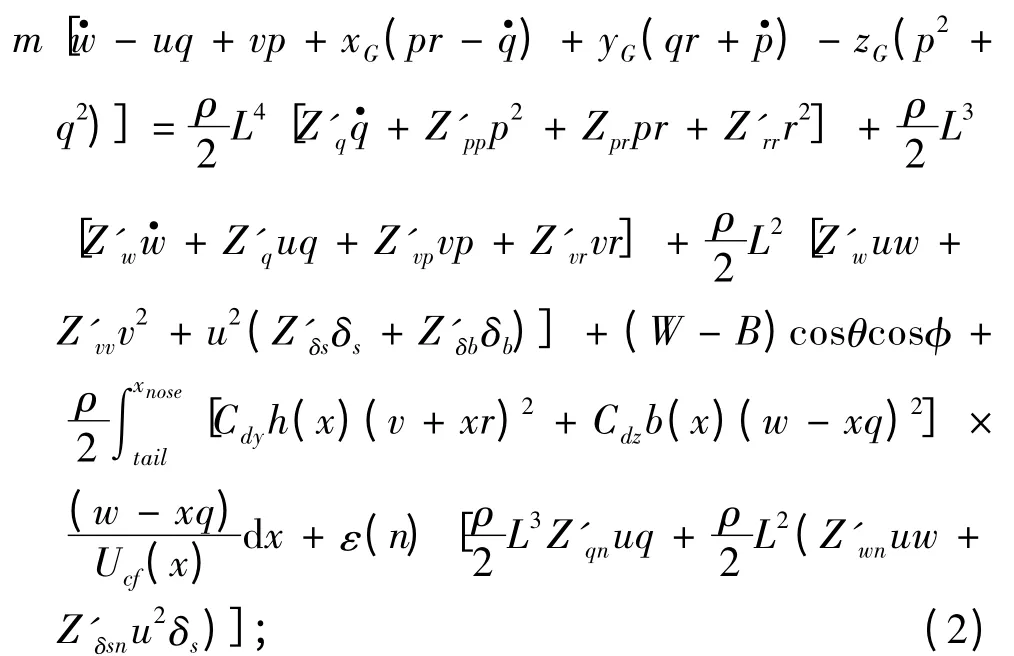
3)橫搖力矩方程

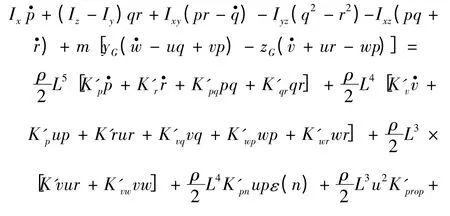
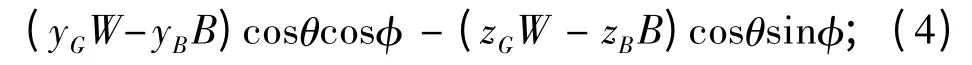
4)縱傾力矩方程

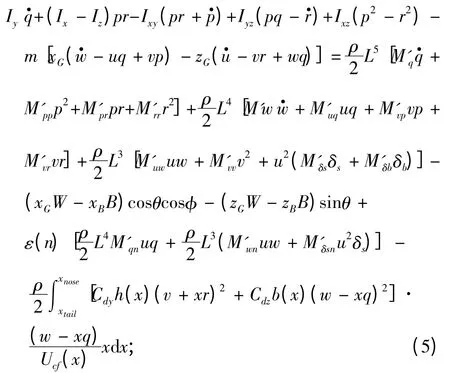
5)偏航力矩方程

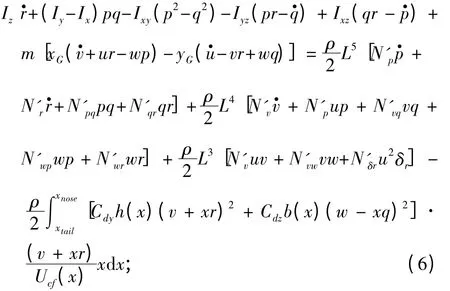
6)運動關系式

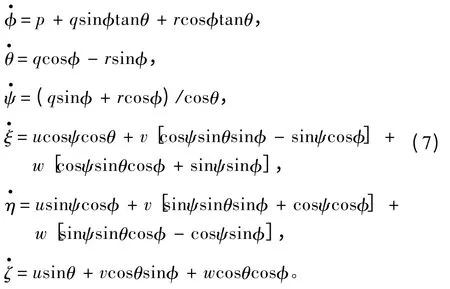
式中:運動坐標系(簡稱動系)O-xyz 固聯于潛艇艇體上;u，v，w 分別為縱向速度、橫向速度、垂向速度;p，q，r 分別為橫傾角速度、縱傾角速度、偏航角速度;φ，θ，Ψ 分別為橫傾角、縱傾角、航向角;W 為潛艇重力;B 為潛艇浮力;δr，δb，δs分別為方向舵舵角、首升降舵舵角、尾升降舵舵角;xG，yG，zG為重心坐標;xB，yB，zB為浮心坐標;n 為螺旋槳轉速;其他參數意義參照文獻［2］和文獻［5］;右上角帶“′”的項為水動力系數項，其值及其他參數值大小參考文獻［7］。

2 潛艇水下回轉運動仿真

2.1 Matlab 建模

上述數學模型中使用了積分表達式，這給實際工程應用帶來不便。由積分學的原理可知，積分是將物體分成無限段再求和，而在實際工程運用當中不可能進行無限分段，只能進行有限分段再求和，分段越多，積分精度越高，但計算越復雜;而分段越少，計算越簡單，但不利于積分精度。所以本文借鑒積分學的思想，采用一種沿x 軸各點分布的近似計算方法——分段計算方法，對潛艇水下回轉運動橫向水動力進行計算，即將潛艇沿艇長方向平均分成若干段，以每段中心點的橫向水動力作為整段的平均橫向水動力，計算各段的受力情況，再將各段的力進行矢量相加，求出整艇的橫向水動力。為了減少計算量，同時又保證足夠的計算精度，找到一個合理的分段數是必要的。針對本文的研究對象，經分析研究認為將潛艇沿艇長方向等分為10 段來近似計算艇體的受力情況已經足夠簡便和準確，故將潛艇沿艇長方向等分為10 段，并用Matlab 軟件進行建模。

2.2 運動參數仿真

潛艇水下回轉可根據運動過程中參數的變化特點將其分為轉舵階段、過渡階段和定常階段［1］，本文研究的是潛艇水下回轉運動進入定常階段時漂角βs、回轉角速度rs、橫傾角Φs以及縱傾角θs隨方向舵舵角δr和航速U 的變化規律。設定在無限深、廣、靜的流場中，以上述Matlab 仿真模型為基礎，分別設定仿真航速U 為4 kn，8 kn，12 kn，16 kn，19 kn，21 kn，22 kn;分別操5°，9°，12°，14°和15°方向舵，仿真計算結果如表2 所示。

2.3 仿真結果分析

分析表2 可知，潛艇水下定常回轉運動時:

1)漂角隨著方向舵舵角的增大而增大，但隨航速的變化不大。由此可知，漂角的大小主要受方向舵舵角的影響而與航速關系不大。潛艇小舵角回轉時，漂角隨舵角線性增長，但大舵角運動時(如大于12°)，增長趨勢呈非線性化，如圖1 所示。

2)回轉角速度分別隨著方向舵舵角和航速的增大而增大。

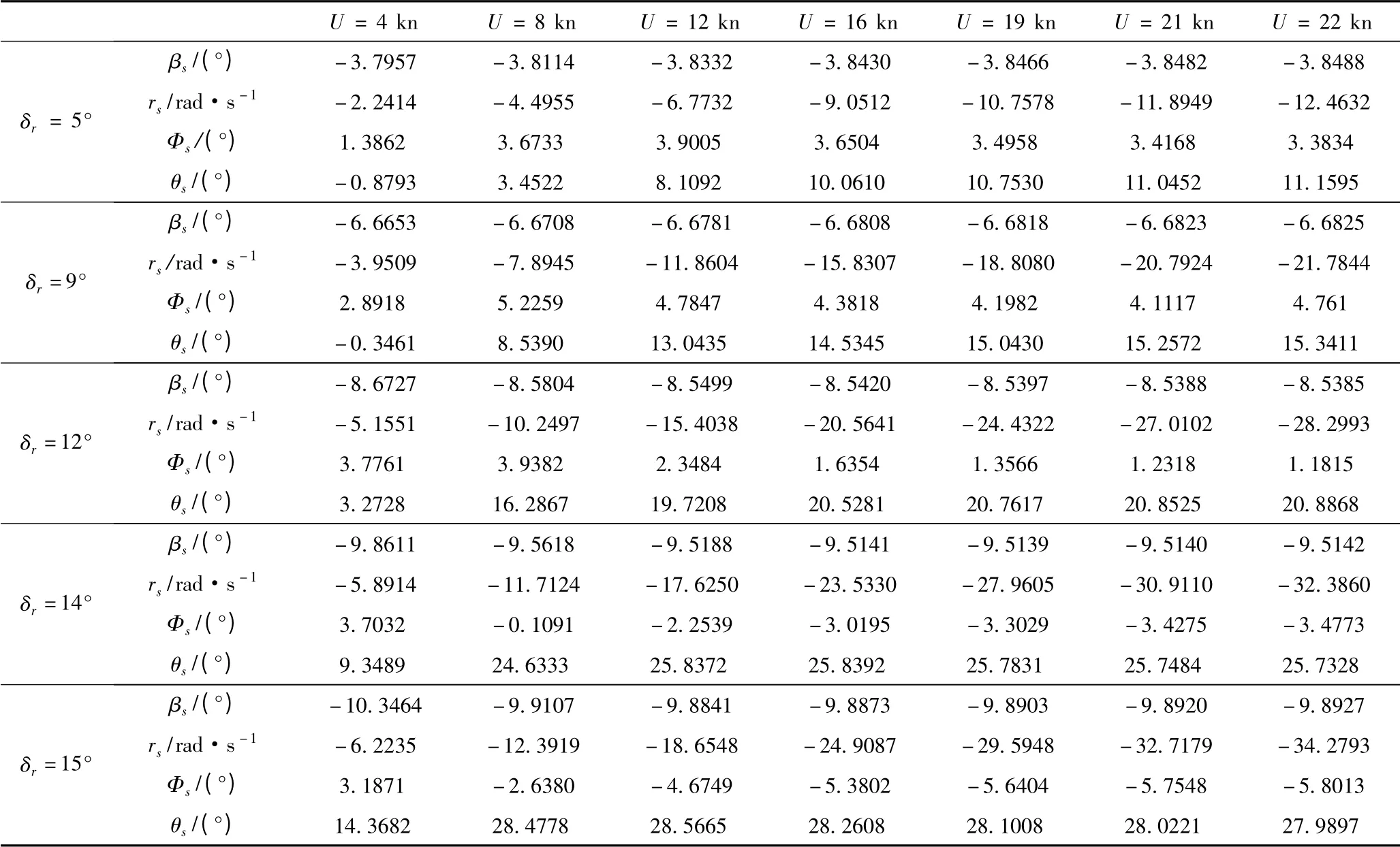
表2 潛艇水下定常回轉運動參數Tab.2 The parameters of submarine in steady rotary movement under water

①航速不變時，隨著方向舵舵角的增大，橫傾角先增大后快速減小，潛艇由內傾變為外傾，如圖2 所示，小舵角時，使潛艇內傾的艇體橫向力對潛艇橫傾起主要貢獻作用，潛艇內傾，隨著舵角的增大，漂角增大，但艇體橫向水動力增大的速度大于方向舵舵力的增大速度，內傾角繼續增大。當舵角增大到某一值后，隨著舵角的增大，艇體橫向力增大的速度小于方向舵舵力的增大速度，最終艇體橫向水動力小于方向舵舵力的橫向分量，于是艇體橫傾角出現先增大后快速減小、由內傾變為外傾的現象。

②方向舵舵角一定時，可分以下2 種情況(見圖3):一是小舵角(如小于12°)回轉時，橫傾角隨著航速的增大先增大后緩慢減小。這主要是因為潛艇小舵角回轉時，使潛艇內傾的艇體橫向力對潛艇橫傾起主要貢獻作用，隨著航速的增大，艇體橫向力增大，橫傾角也相應增大，但是，與此同時，使潛艇外傾的舵橫向分力也逐漸增大，且幅度大于艇體橫向力增長的幅度。所以橫傾角隨著航速的增大呈先增大后緩慢減小的變化趨勢。二是大舵角回轉時，艇體隨著航速的增大逐漸由內傾變為外傾。這是因為低航速回轉時，艇體橫向力大于舵橫向分力，所以艇體呈內傾姿態，之后隨著航速的增大，舵橫向分力迅速增大，直到大于艇體橫向力，潛艇由內傾變為外傾。

3)小舵角、低航速的情況下潛艇呈首傾狀，即縱傾角小于0，此時若保持航速不變，方向舵舵角逐漸增大，則縱傾角將由首傾變為尾傾，并逐漸增大，如圖4 所示;若保持方向舵舵角不變，航速增大，則縱傾角逐漸增大同時增大幅度放緩，直至基本保持最大值不變，如圖5 所示。

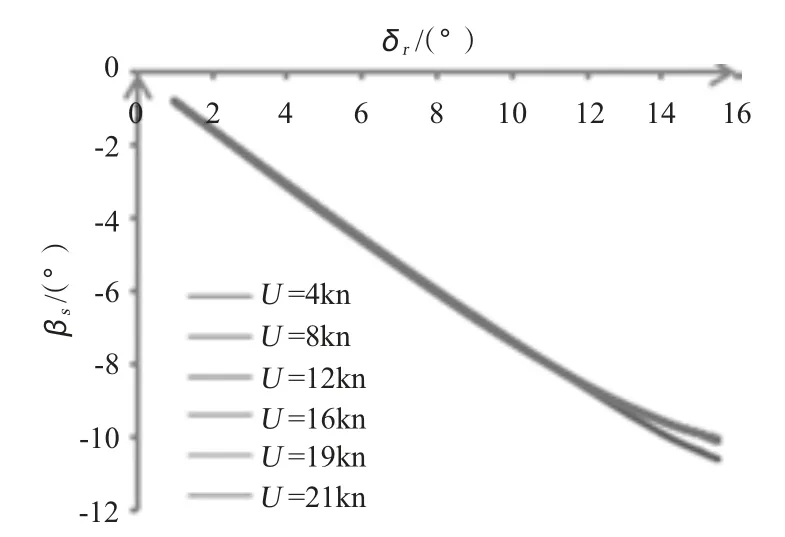
圖1 βs 隨δr 的變化情況Fig.1 βs versus δr

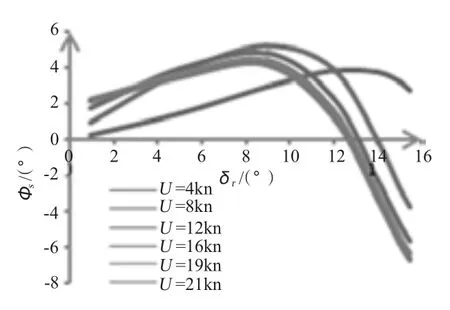
圖2 Φs 隨δr 的變化情況Fig.2 Φs versus δr

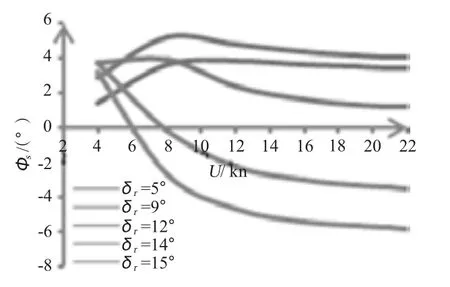
圖3 Φs 隨U 的變化情況Fig.3 Φs versus U

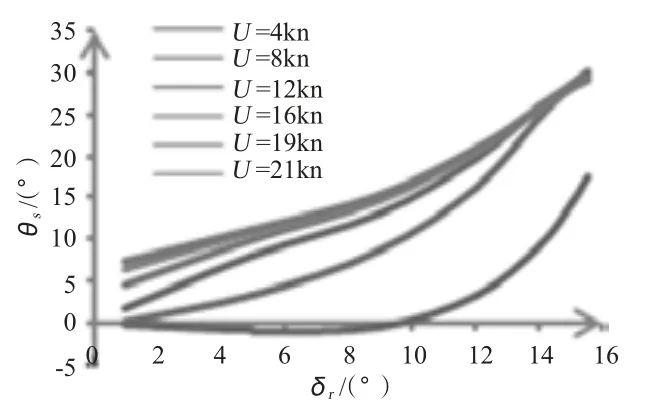
圖4 θs 隨δr 的變化情況Fig.4 θs versus δr

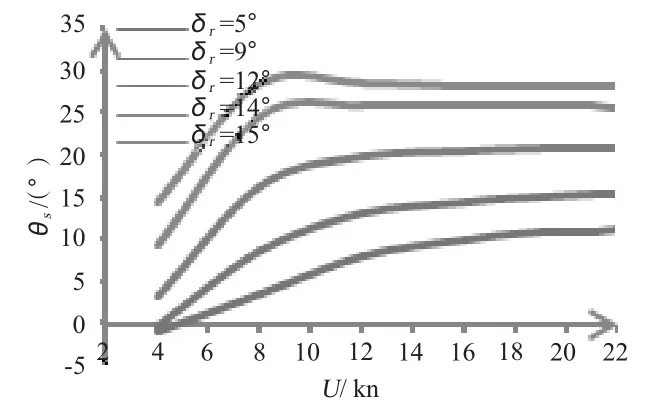
圖5 θs 隨U 的變化情況Fig.5 θsversus U

由上述分析可知，仿真結果與理論分析和實艇操縱規律基本一致，從而說明本文所用潛艇數學模型和建模仿真方法正確有效。潛艇水下回轉運動進入定常階段時，艇體以一定的角速度作等速圓周運動，同時存在明顯的橫傾、縱傾等耦合運動現象，這與潛艇回轉運動時存有較大的非線性成分有關。尤其當潛艇高速大舵角回轉時，橫向流突出，艇體上所受流體動力和力矩的大小與航速、漂角以及回轉角速度等因素密切相關，此時潛艇運動參數超出了常規的線形范圍，不能用線性方程進行求解［1］。從式(2)亦知，潛艇橫向受力方程中存在眾多高次項、耦合項等非線性項，所以有必要進一步開展潛艇水下回轉運動非線性分析。

3 結 語

本文對67 方程和79 方程進行對比分析，得出了合理有效的潛艇水下回轉運動數學模型，借鑒積分理論的思想，采用分段計算方法對潛艇水下回轉運動橫向水動力進行建模仿真，重點分析了潛艇水下定常回轉運動時參數的變化規律，其結果與實艇操縱規律基本一致，從而說明本文所用潛艇數學模型和建模仿真方法是正確有效的。研究表明，潛艇水下回轉運動時存在明顯的橫傾、縱傾等耦合運動現象，潛艇橫向受力方程中存在眾多高次項、耦合項等非線性項，艇體運動參數超出了常規的線形范圍，不能用線性方程進行求解，所以下一步有必要開展潛艇水下回轉運動非線性研究。

［1］施生達.潛艇操縱性［M］.北京:國防工業出版社，1995.SHI Sheng-da. Submarine maneuverability［M］. Beijing:Notional Defence Industry Press，1995.

［2］MORTON G，GRENT R H.Standard equations of motion for submarine simulation［R］.AD-653，861，SNAME，1967.

［3］林雄偉，胡大斌，戴余良. 潛艇非線性運動研究綜述［J］.船舶力學，2013，17(1 -2):187 -195.LIN Xiong-wei，HU Da-bin，DAI Yu-liang. Overview on the research of submarine nonlinear motion［J］. Journal of Ship Mechanics，2013，17(1 -2):187 -195.

［4］林俊興，倪剛，戴余良，等.潛艇定常回轉運動參數變化規律研究［J］.艦船科學技術，2014，36(1):31 -37.LIN Jun-xing，NI Gang，DAI Yu-liang，et al.Research on parameters′change rule of submarine′s steady rotary movement［J］.Ship Science and Technology，2014，36(1):31-37.

［5］FELDMAN J.DTNSRDC revised standard submarine equations of motion［R］.DTNSRDC Report SPD，1979:393-09.

［6］倪剛，林俊興，唐成，等.修正的潛艇標準運動方程的應用［J］.艦船科學技術，2013，35(11):41 -44.NI Gang，LIN Jun-xing，TANG Cheng，et al.Applied study of submarine′s standard movement equation of the revise［J］.Ship Science and Technology，2013，35(11):41-44.

［7］HEALEY A J，LIENARD D. Multivariable sliding mode control for autonomous diving and steering of unmanned underwater vehicles ［J］. IEEE Journal of Ocean Engineering，1993，18(3):327 -339.

［8］BONCAL R J.A study of model based maneuvering controls for autonomous underwater vehicles［D］. California:Naval Postgraduate School，1987.