基于CMOR 的跳頻信號(hào)參數(shù)盲估計(jì)算法

萬(wàn)喬喬，張俊然，龔曉峰

（四川大學(xué) 電氣信息學(xué)院，四川 成都610065）

0 引 言

如何有效地提取跳頻信號(hào)的各性能參數(shù)并對(duì)其進(jìn)行實(shí)時(shí)監(jiān)測(cè)，以提高頻譜資源利用率，是當(dāng)前無(wú)線電頻率檢測(cè)管理首要解決的問(wèn)題［1，2］。傳統(tǒng)的利用短時(shí)傅里葉變換（STFT）提取性能參數(shù)的主要做法是，人為地選擇一合適大小的矩形窗，并對(duì)信號(hào)做STFT 變換以從時(shí)頻分布圖上提取跳頻頻率和跳速等，雖然可以提取，但是固定矩形窗的大小嚴(yán)重影響著參數(shù)的估計(jì)精度［3］；而一般意義上的先利用小波變換［4］，再在頻譜圖上求跳速的方法雖然理論上可行，但是由于具體復(fù)雜的電磁環(huán)境及實(shí)際環(huán)境中的噪聲干擾等問(wèn)題，其可行性較差。

本文基于CMOR，通過(guò)充分挖掘Morlet小波系數(shù)的尺度與跳頻信號(hào)頻率之間的一種內(nèi)在聯(lián)系，準(zhǔn)確地得到了跳頻信號(hào)的時(shí)頻分布圖［5］，再?gòu)臅r(shí)頻分布圖準(zhǔn)確地估計(jì)出跳頻信號(hào)的跳頻頻率。再利用sym4 （symlets函數(shù)系symN （N＝2，3，…，8）的縮寫(xiě)）小波分解較高的濾波特性，準(zhǔn)確地估計(jì)出跳頻信號(hào)的邊緣跳變點(diǎn)，進(jìn)而估計(jì)出了跳頻周期與跳速等參數(shù)。目前大多數(shù)算法只是建立在分析理想信號(hào)的基礎(chǔ)上，缺乏實(shí)際應(yīng)用測(cè)試，本文不僅用仿真信號(hào)對(duì)算法進(jìn)行了說(shuō)明，還用信號(hào)源N5182A （Agilent N5182A3G／6G MXG 射 頻 矢 量 信 號(hào) 發(fā)生器，頻率范圍是250KHz至3GHz或6GHz，其射頻與微波：寬帶I／Q 調(diào)制）發(fā)出的實(shí)際的跳頻信號(hào)進(jìn)行了測(cè)試，較高的實(shí)時(shí)性和準(zhǔn)確性說(shuō)明所提算法具有較高的實(shí)際應(yīng)用價(jià)值。

1 Morlet小波變換原理

連續(xù)小波變換 （CWT）的定義見(jiàn)參考文獻(xiàn) ［6－8］，其表達(dá)式為

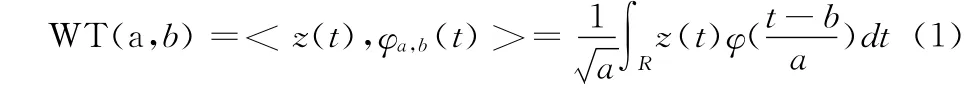
由式 （1）可以看出，小波變換是一種積分變換，稱WT（a，b）為小波變換系數(shù)。其中更重要的是，小波基具有尺度因子a和平移因子b。

Morlet函數(shù)小波是以單頻率復(fù)正弦方式調(diào)制的一種高斯波，它的時(shí)、頻表達(dá)式如下：時(shí)域表達(dá)式

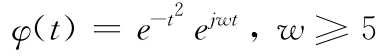
頻域表達(dá)式

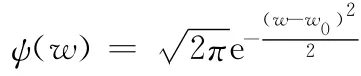
從時(shí)域表達(dá)式上看，w 只影響φ（t）虛部，顯然w 的值不同，φ（t）的包絡(luò)區(qū)域不會(huì)變，只是包絡(luò)區(qū)對(duì)應(yīng)的正弦波形的頻率會(huì)改變；從頻域表達(dá)式看，當(dāng)w0＝w0′時(shí)，ψ（w）的中心頻率會(huì)變?yōu)閣′0，但是帶寬保持不變；因此Morlet小波函數(shù)實(shí)際上是一種復(fù)小波變換，其在時(shí)、頻域都具有良好的局域特性，常常用于時(shí)頻分析以及復(fù)信號(hào)的分解中。

Morlet小波變換見(jiàn)參考文獻(xiàn) ［9－11］，其離散化形式為

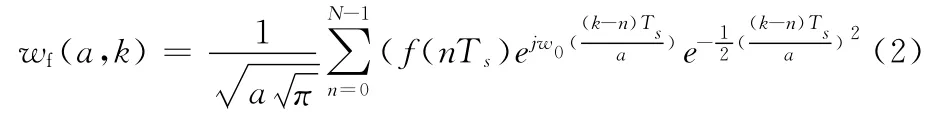
式 （2）中對(duì)應(yīng)于某給定尺度a 的信號(hào)子波變換的結(jié)果就相當(dāng)于濾波器的時(shí)域輸出，輸出的瞬時(shí)功率是返回系數(shù)模值的平方，a取不同的值就代表在不同的頻段對(duì)信號(hào)的功率譜進(jìn)行估計(jì)。總結(jié)來(lái)說(shuō)，Morlet小波變換的實(shí)質(zhì)就是其具有帶通濾波特性，以此清晰地觀察到信號(hào)的邊緣跳變點(diǎn)等性能參數(shù)。應(yīng)的尺度序列 （矩陣的行），亮度的深淺代表CMOR 變換系數(shù)幅值的大小，顏色越亮的地方CMOR 的系數(shù)值越大。取CMOR 系數(shù)模值在各個(gè)時(shí)間點(diǎn)的最大值，得到信號(hào)的跳變規(guī)律如圖2所示。

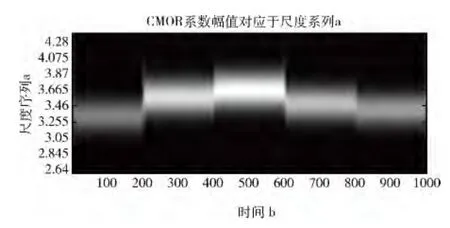
圖1 CMOR 時(shí)頻圖

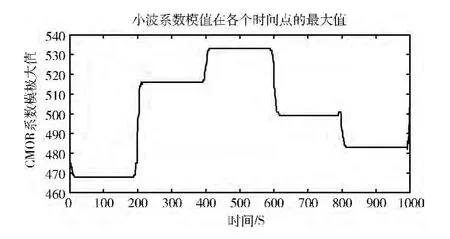
圖2 CMOR 系數(shù)模極大值

圖2可以看出CMOR 系數(shù)模值已經(jīng)很好地反應(yīng)了跳頻信號(hào)頻率跳變的規(guī)律，但是在跳變點(diǎn)存在抖動(dòng)和尖峰，為了消除在上升沿或下降沿存在的這種抖動(dòng)和尖峰，本文采用離散小波分解對(duì)信號(hào)進(jìn)行濾波，具體做法是：采用sym4小波對(duì)CMOR 系數(shù)模極大值序列做三層分解，并且取其低頻系數(shù)進(jìn)行重構(gòu)。取平滑處理后小波系數(shù)模值的第一跳來(lái)說(shuō)明濾波效果，如圖3所示。

2 基于小波的跳頻信號(hào)參數(shù)估計(jì)算法

跳頻信號(hào)參數(shù)盲估計(jì)，主要包括跳頻信號(hào)的周期、跳速及其跳頻圖案。本文先用MATLAB 生成的跳頻信號(hào)來(lái)驗(yàn)證算法，根據(jù)常規(guī)接收機(jī)系統(tǒng)中碼速率和采樣率的取值關(guān)系，在這里選取碼速率為100Hz，采樣率為20倍的碼速率，跳變次數(shù)5次，總共1000個(gè)采樣點(diǎn)數(shù)。跳頻周期為5 ms，跳頻頻率集為 ｛f1＝200 Hz，f2＝320 Hz，f3＝360 Hz，f4＝280 Hz，f5＝240 Hz｝［12］。對(duì)此信號(hào)做CMOR，選擇Morlet復(fù)小波的中心頻率fc＝3；帶寬db＝3；尺度scall＝ ［1：0.005：5］。CMOR 之后得到信號(hào)的時(shí)頻分布圖如圖1所示。

CMOR 的返回系數(shù)是一個(gè)矩陣，在圖1中，橫軸代表時(shí)間，對(duì)應(yīng)信號(hào)的采樣點(diǎn) （矩陣的列），縱軸是CMOR 對(duì)

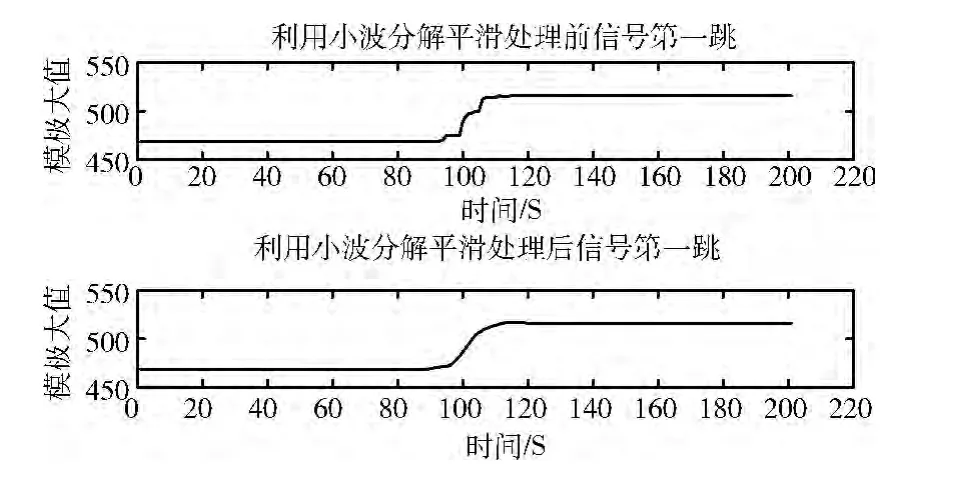
圖3 CMOR 系數(shù)模極大值對(duì)應(yīng)于信號(hào)的第一跳

對(duì)濾波處理后的信號(hào)再進(jìn)行求導(dǎo)操作，來(lái)捕獲信號(hào)跳變點(diǎn)的準(zhǔn)確位置，如圖4所示。

并對(duì)求導(dǎo)后的曲線進(jìn)行 “譜峰搜索”準(zhǔn)確捕獲跳變時(shí)刻以及跳速，統(tǒng)計(jì)結(jié)果見(jiàn)表1。

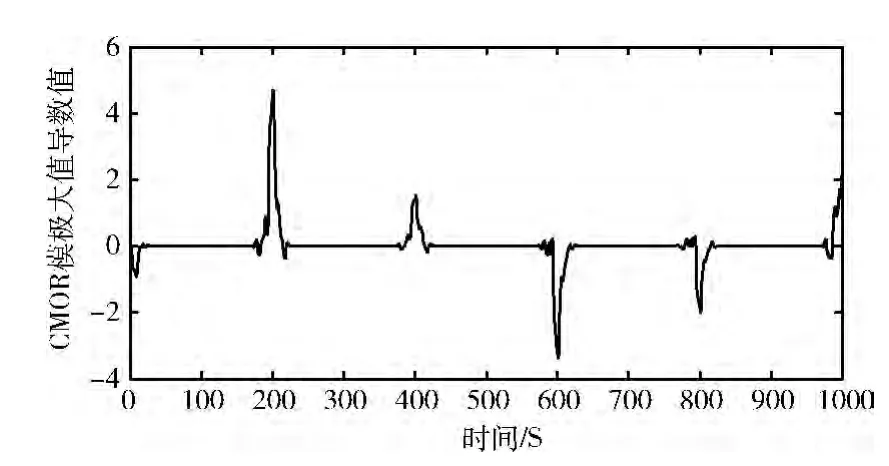
圖4 信號(hào)的跳變時(shí)刻

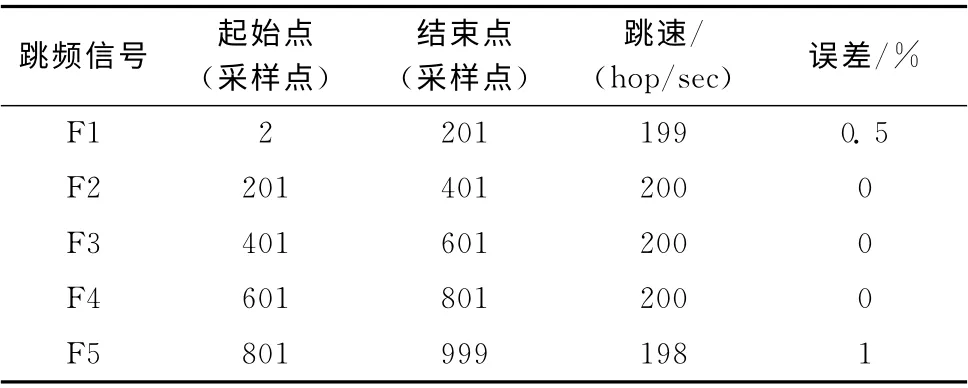
表1 跳變時(shí)刻

對(duì)表1的跳速求平均值，得到跳速V＝ （199＋200＋200＋200＋198）／5＝199.4 （hop／s），即 每 秒199.4 跳；然后再根據(jù)公式T＝1／V，得到跳頻信號(hào)的跳頻周期T＝5.02ms。

在估計(jì)出跳變時(shí)刻的基礎(chǔ)上，再次充分挖掘CMOR 系數(shù)的實(shí)質(zhì)含義，研究發(fā)現(xiàn)有如下關(guān)系式：Fa＝Fc×fs／A，其中Fc為小波的中心頻率，fs為信號(hào)的采樣率，A 為尺度，F(xiàn)a為對(duì)應(yīng)的跳頻頻率。得到了Fa就得到了跳頻信號(hào)的時(shí)間－頻率曲線，如圖5所示。相應(yīng)的跳頻信號(hào)的頻率值見(jiàn)表2。

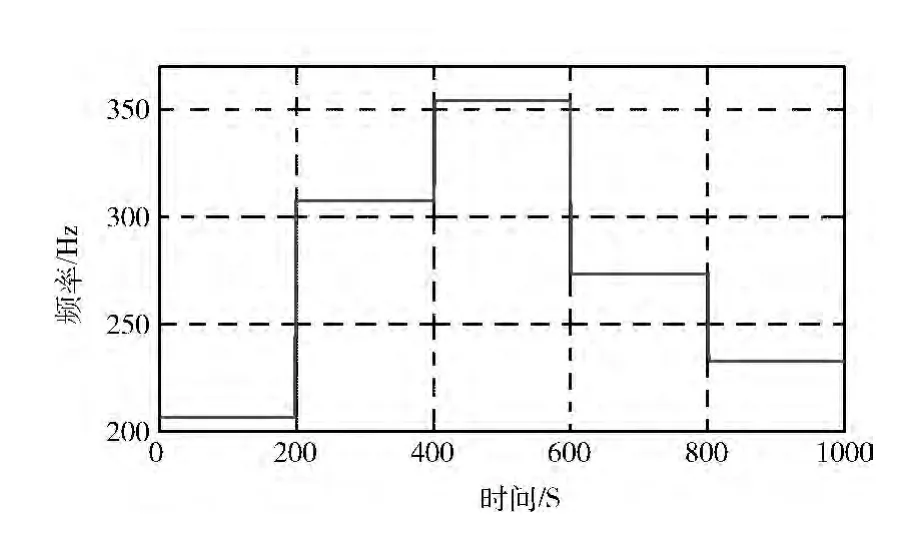
圖5 跳頻信號(hào)的時(shí)間－頻率曲線

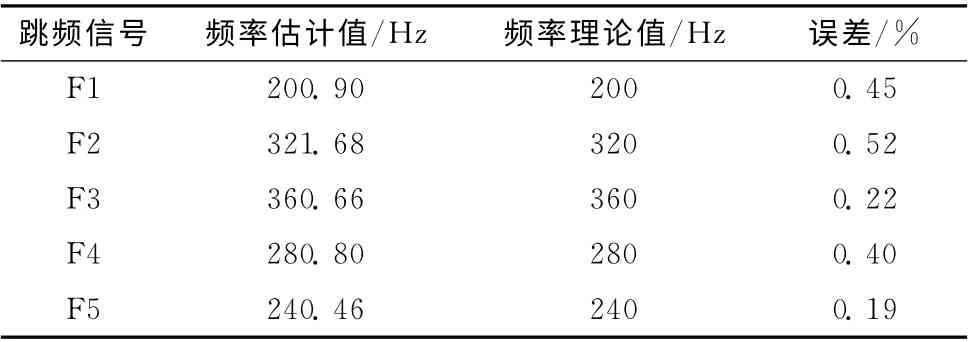
表2 跳頻信號(hào)頻率

以上仿真結(jié)果顯示，CMOR 算法可以準(zhǔn)確捕獲到信號(hào)的跳變時(shí)刻，并求出其跳頻頻率。基于CMOR 的跳頻信號(hào)參數(shù)估計(jì)算法流程如下：①選擇合適的尺度，對(duì)信號(hào)做一維連續(xù)小波變換，并求得小波變換系數(shù)的模極大值；②對(duì)小波變換系數(shù)的模極大值做3 層尺度’sym4’小波分解，取其分解后的低頻系數(shù)進(jìn)行重構(gòu)，相當(dāng)于對(duì)信號(hào)進(jìn)行低通濾波，去除高頻干擾；③對(duì)濾波處理后的模極大值序列進(jìn)行求導(dǎo)操作，捕獲其跳變時(shí)刻；據(jù)跳變時(shí)刻求出跳頻信號(hào)周期，其倒數(shù)即為跳頻信號(hào)的跳速；④根據(jù)Morlet小波變換系數(shù)模極大值序列的尺度序列與跳頻信號(hào)頻率之間的內(nèi)在聯(lián)系，求得跳頻信號(hào)的頻率值。

3 算法驗(yàn)證

3.1 實(shí)驗(yàn)平臺(tái)搭建

由于仿真信號(hào)是在理想環(huán)境下，本文用實(shí)測(cè)信號(hào)來(lái)驗(yàn)證算法的合理性。實(shí)驗(yàn)用的信號(hào)源是N5182A，在華日通訊技術(shù)有限公司的實(shí)驗(yàn)基地，信號(hào)源經(jīng)一個(gè)天線發(fā)射出去，經(jīng)空中傳播后，再由另一個(gè)連接接收機(jī)的天線接收，接收機(jī)為雙通道接收機(jī)PXI－1045，信號(hào)采用正交的采樣方式，其中I是同相分量，Q 是正交分量，實(shí)驗(yàn)平臺(tái)如圖6所示。

圖6 實(shí)驗(yàn)平臺(tái)

3.2 跳頻信號(hào)測(cè)試

信號(hào)源N5182A 發(fā)出的跳頻信號(hào)，其采樣帶寬為100 kHz，中心頻率為88.05 MHz，采樣率為125kHz，每幀長(zhǎng)度為65536，跳頻周期為80ms。為了驗(yàn)證算法的合理性和實(shí)用性，在一天的不同時(shí)間段在接收機(jī)端連續(xù)采集跳頻信號(hào)，并對(duì)每次采集的信號(hào)進(jìn)行100多次測(cè)試，在這里任選其中幾組，觀察其在每個(gè)跳變點(diǎn)的信息。跳頻信號(hào)的頻譜如圖7所示。

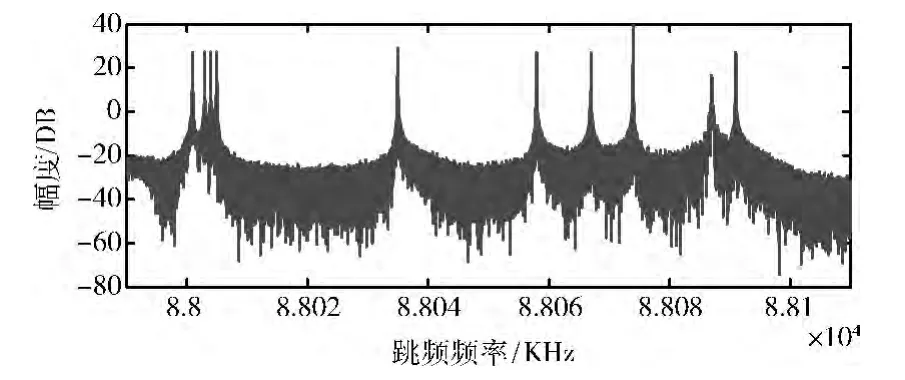
圖7 實(shí)測(cè)跳頻信號(hào)頻譜

對(duì)測(cè)試信號(hào)進(jìn)行CMOR，且平滑濾波處理前后的信號(hào)如圖8所示。得到最終的時(shí)頻曲線如圖9所示。

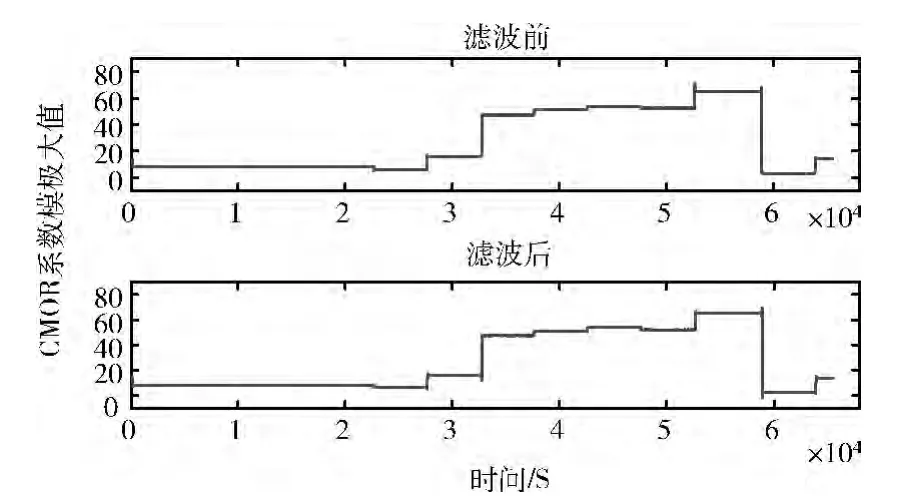
圖8 CMOR 模極大值濾波前后

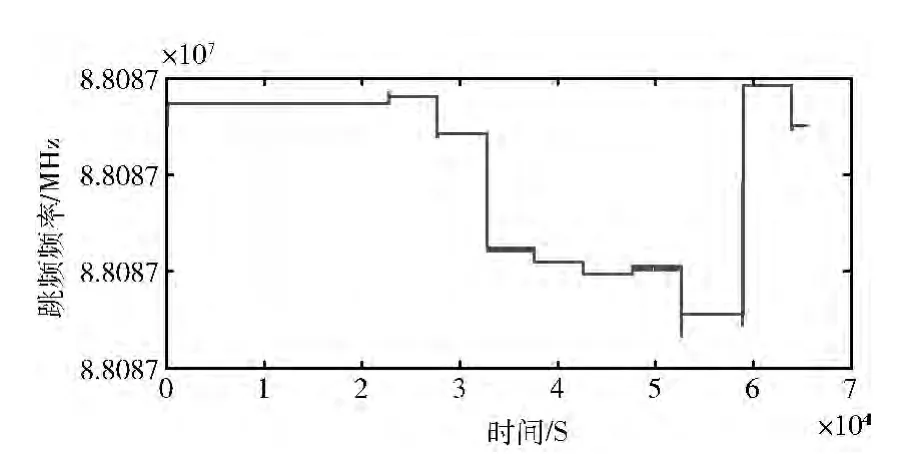
圖9 跳頻信號(hào)的時(shí)間－頻率曲線

跳頻信號(hào)的跳速和跳頻頻率分別見(jiàn)表3和表4。

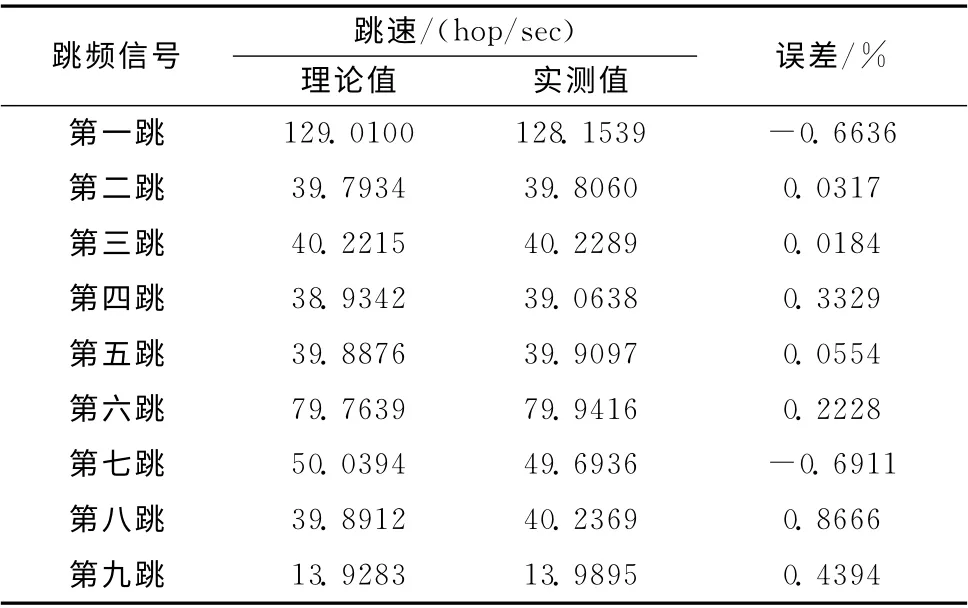
表3 Morlet復(fù)小波估計(jì)跳速

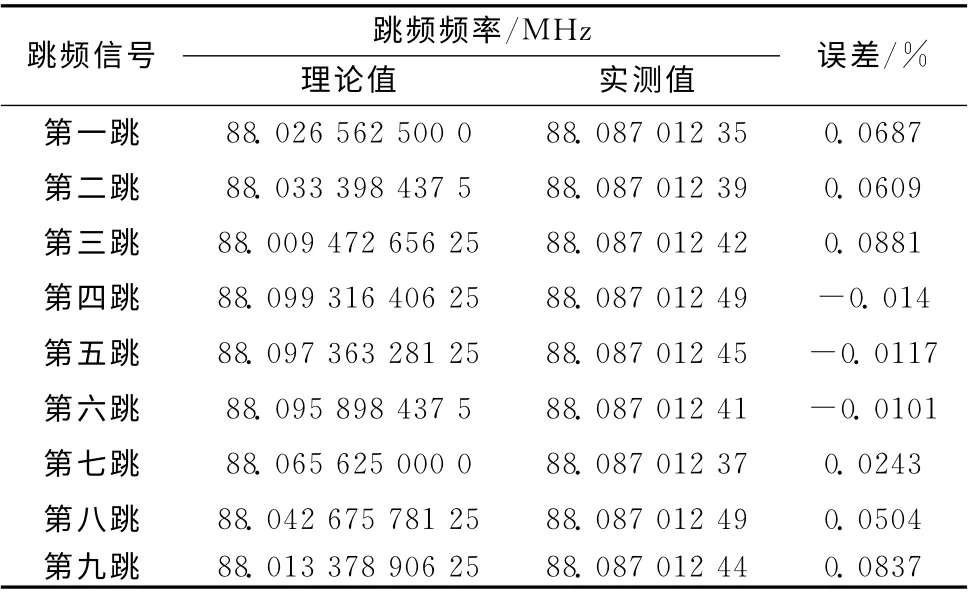
表4 Morlet復(fù)小波估計(jì)跳頻頻率

為了更直觀地顯示結(jié)果，對(duì)不同時(shí)間段的跳頻信號(hào)的跳速和跳頻頻率分別做誤差曲線評(píng)估，如圖10、圖11 所示，其中縱坐標(biāo)分別代表跳速和跳頻頻率理論值與估計(jì)值的相對(duì)誤差。

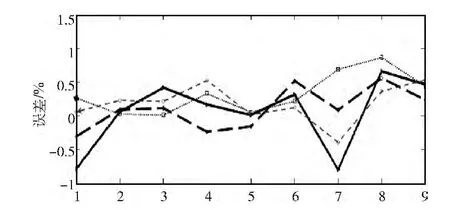
圖10 跳速誤差評(píng)估曲線

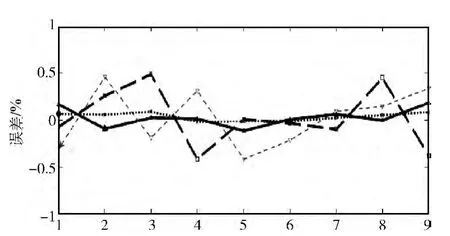
圖11 跳頻頻率誤差評(píng)估曲線

圖10和圖11的跳速和跳頻頻率的誤差評(píng)估曲線顯示，基于Morlet小波的新的跳頻信號(hào)參數(shù)盲估計(jì)算法，其估計(jì)誤差的絕對(duì)值均小于1%。為了說(shuō)明新的算法在估計(jì)精度方面的優(yōu)勢(shì)，將其與其他算法的結(jié)論做對(duì)比：文獻(xiàn) ［13］的結(jié)論見(jiàn)表5；文獻(xiàn) ［14］的結(jié)論見(jiàn)表6，表6中mi代表每一個(gè)跳變點(diǎn)，Th代表每一跳的駐留時(shí)間，由此計(jì)算出跳頻周期的估計(jì)值與真實(shí)值的平均相對(duì)誤差為±1.82%。

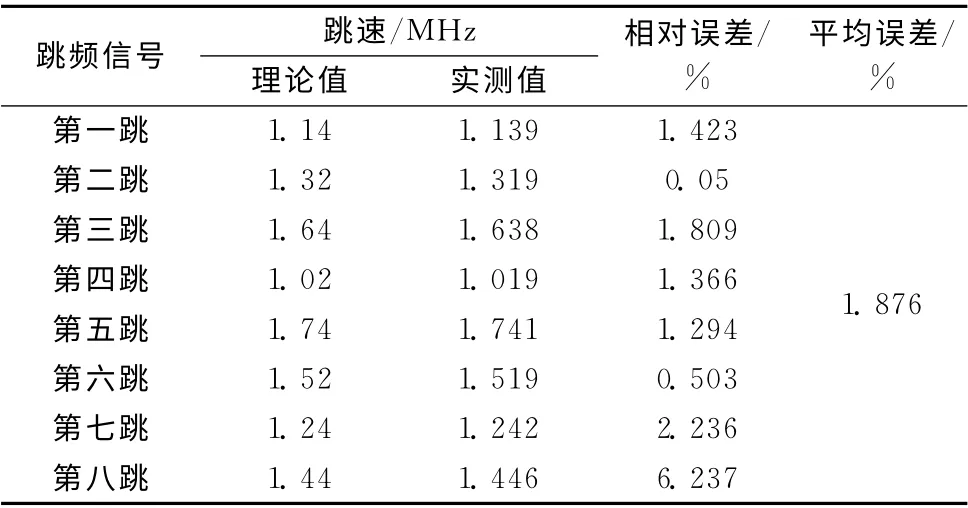
表5 文獻(xiàn) ［13］表4.2的跳頻頻率估計(jì)值

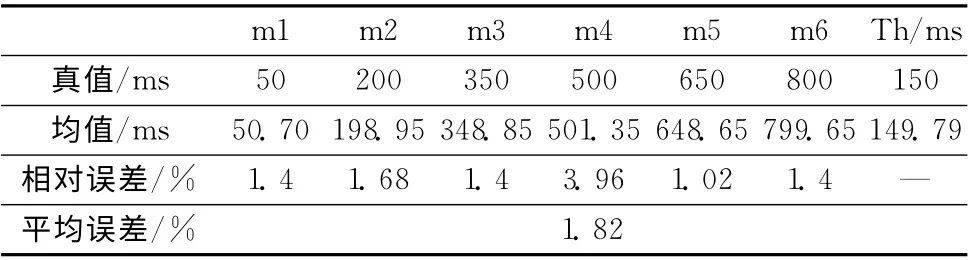
表6 文獻(xiàn) ［14］表1的跳頻周期估計(jì)值

對(duì)比顯示，新算法的估計(jì)精度更高。

4 結(jié)束語(yǔ)

本文通過(guò)充分挖掘Morlet小波變換后小波系數(shù)所代表的本質(zhì)含義，即利用小波系數(shù)模極大值對(duì)應(yīng)的尺度與測(cè)試信號(hào)頻率之間的密切關(guān)系，提出了一種新的基于CMOR 的跳頻信號(hào)參數(shù)盲估計(jì)算法，以達(dá)到參數(shù)估計(jì)的目的。仿真和實(shí)測(cè)信號(hào)結(jié)果均表明，新的算法準(zhǔn)確地估計(jì)出了跳頻信號(hào)的各性能參數(shù)，而且估計(jì)精度很高。此算法可以適應(yīng)于目前常用的數(shù)字接收機(jī)系統(tǒng)中，并在接收機(jī)系統(tǒng)中已經(jīng)得到了初步的應(yīng)用。但是如果將此方法用于分析目前學(xué)術(shù)界正在探索的變跳速的跳頻信號(hào)，還存在一定的局限性。此外還可以考慮對(duì)算法進(jìn)行進(jìn)一步的改進(jìn)，如跳頻信號(hào)的調(diào)制識(shí)別、通信對(duì)抗中信號(hào)的偵察與接收、高跳速跳頻電臺(tái)的干擾研究及跳頻電臺(tái)的同步等問(wèn)題。

［1］CHEN Feng.Real－time spectrum detection system ［J］.Railway Technology Innovation，2011 （6）：47－49 （in Chinese）.［陳峰.實(shí)時(shí)頻譜偵測(cè)系統(tǒng) ［J］.鐵路技術(shù)創(chuàng)新，2011 （6）：47－49.］

［2］LIU Qi，SU Wei，LI Chengshu，et al.Adaptive spectrum sharing scheme based on FH communications ［J］.Acta Electronica Sinica，2010，38 （1）：105－110 （in Chinese）.［劉琪，蘇偉，李承恕.基于跳頻的自適應(yīng)頻譜共享方案 ［J］.電子學(xué)報(bào)，2010，38 （1）：105－110.］

［3］ZHANG Wei.Radio frequency up cost special fund collection，management，policy analysis ［J］.China Radio，2013 （5）：18－20 （in Chinese）.［張偉.無(wú)線電頻率占用費(fèi)專項(xiàng)資金收取、管理政策解析 ［J］.中國(guó)無(wú)線電，2013 （5）：18－20.］

［4］ZHOU Lu，WU Qian，LUO Chaohong，et al.A new kind of frequency hopping signal jump speed blind estimation algorithm［J］.Telecommunications Technology，2008，48 （8）：73－77（in Chinese）.［周露，吳潛，羅朝洪.一種新的跳頻信號(hào)跳速盲估計(jì)算法 ［J］.電訊技術(shù)，2008，48 （8）：73－77.］

［5］Deng Fang，Chen Jie，Chen Chen.Adaptive unscented Kalman filter for parameter and state estimation of nonlinear highspeed objects ［J］.Journal of Systems Engineering and Electronics，2013，24 （4）：655－665.

［6］Zhang Lei，Li Yachao，Liu Yan，et al.Time－frequency characteristics based motion estimation and imaging for high speed spinning targets via narrowband waveforms［J］.Science China（Information Sciences），2010，53 （8）：1628－1640.

［7］MAO Zhongyang，ZHAO Peihong，WANG Hongxing，et al.A non－stationary signal analysis based on the phase modulation signal demodulation algorithm ［J］.Journal of Naval Aeronautical Engineering Institute，2012，27 （5）：525－529 （in Chinese）.［毛忠陽(yáng)，趙培洪，王紅星，等.一種基于非平穩(wěn)信號(hào)分析的時(shí)相調(diào)制信號(hào)解調(diào)算法 ［J］.海軍航空工程學(xué)院學(xué)報(bào)，2012，27 （5）：525－529.］

［8］ZHANG Yaqi，CAI Hua.Based on DFT，DCT and wavelet transform image compression with Matlab ［J］.Computer Knowledge and Technology，2013 （21）：4929－4932 （in Chinese）.［張雅琪，才華.基于DFT、DCT 和小波變換圖像壓縮 與 Matlab 實(shí) 現(xiàn) ［J］.電 腦 知 識(shí) 與 技 術(shù)，2013 （21）：4929－4932.］

［9］LIU Jiantao.Frequency hopping signal blind parameter estimation algorithm research and implementation ［D］.Chengdu：University of Electronic Science and Technology，2007 （in Chinese）.［劉健濤.跳頻信號(hào)參數(shù)盲估計(jì)算法研究及實(shí)現(xiàn) ［D］.成都：電子科技大學(xué)，2007.］

［10］FENG Tao，YUAN Chaowei.Frequency hopping signal，a new method of time－frequency analysis［J］.Journal of Beijing University of Posts and Telecommunications，2010，33 （3）：10－14 （in Chinese）. ［馮濤，袁超偉.跳頻信號(hào)的時(shí)頻分析新方法 ［J］.北京郵電大學(xué)學(xué)報(bào)，2010，33 （3）：10－14.］

［11］ZHANG Xi，WANG Xing，DU Xingmin.Based on the wavelet transform parameters of frequency hopping signal blind［J］.Circuit and the Journal of Communication Systems，2009，14 （4）：60－65 （in Chinese）.［張曦，王星，杜興民.基于小波變換的跳頻信號(hào)參數(shù)盲估計(jì) ［J］.電路與通信系統(tǒng)學(xué)報(bào)，2009，14 （4）：60－65.］

［12］LI Chan，CUI Xiaowei，LI Guomin，et al.The phase truncation noise influence in the GPS receiver digital delay lock loop tracking performance analysis［J］.Journal of Tsinghua University （Natural Science Edition）Network，2008，48 （4）：522－525 （in Chinese）. ［李蟬，崔曉偉，李國(guó)民，等.GPS接收機(jī)中相位舍位噪聲影響數(shù)字延遲鎖定環(huán)跟蹤性能的分析［J］.清華大學(xué)學(xué)報(bào) （自然科學(xué)版）網(wǎng)絡(luò)，2008，48 （4）：522－525.］

［13］YU Dan.Frequency hopping signal blind parameter estimation algorithm research ［D］.Dalian：Dalian University of Technology，2008 （in Chinese）.［于丹.跳頻信號(hào)參數(shù)盲估計(jì)算法研究 ［D］.大連：大連理工大學(xué)，2008.］

［14］ZHANG Shichao.Frequency hopping signal blind detection and parameter estimation research ［D］.Chengdu：University of Electronic Science and Technology，2012 （in Chinese）.［張仕超.跳頻信號(hào)的盲檢測(cè)與參數(shù)盲估計(jì)研究 ［D］.成都：電子科技大學(xué)，2012.］