基于三元組的擴頻碼構造及其性能分析

王 慧，吳成茂

（1.西安郵電大學 研究生院，陜西 西安710121；2.西安郵電大學 電子工程學院，陜西 西安710121）

0 引 言

隨著民用通信的頻帶日益擁擠，擴頻通信被廣泛應用于民用領域，并以擴頻通信技術為基礎開發了第三代移動通信 （3G）和第四代移動通信 （4G），擴頻技術傳輸高速數據的能力需要更大的拓展。擴頻技術高速傳輸數據能力的關鍵是傳輸數據的帶寬，而傳輸信號的帶寬主要由擴頻函數決定。因此，探索高效、可靠和安全的擴頻碼［1，2］是擴頻通信研究中的重要使命。

常用的偽隨機序列有線性反饋移位寄存器序列、混沌序列和同余序列。線性反饋移位寄存器序列以m 序列和Gold序列為代表，以其理論簡單、發展完善的特點得到廣泛使用，是擴頻通信中最常使用的擴頻碼。但是其采用線性反饋邏輯，輸出序列完全由初始狀態和反饋函數唯一確定，容易被敵人破譯，即保密性、抗截獲性差。m 序列具有周期性且數量有限、線性復雜度低、第三方易于從擴頻碼的一小段去重建整個序列的問題，其可靠性存在一定的風險，不能滿足大規模通信系統的要求。選用具有混沌特性的序列作為擴頻序列的動態特性會更好［3－5］。

由于Logistic、Tent等混沌序列的初值敏感性和強隨機性，混沌序列構成的擴頻碼也常被使用于擴頻通信。然而由于計算機的計算精度、編譯器、硬件、軟件算法和編程語言的限制，導致在實際計算中混沌序列出現周期性且周期較短的問題。混沌模擬實值序列在傳輸過程中有無限多個狀態，幅度在有限范圍內連續，離散混沌序列是將混沌模擬實值序列進行離散化得到的，但其隨機性和復雜性有了顯著 程度的降低［6－8］。

同余序列與混沌序列一樣，具有初始值和算法參數變化的隨機性，但算法本身是固定的，即一旦初值和算法參數給定，則其生成的隨機序列具有唯一性。同余序列發生器本質是有限域的隨機發生器，不同初始參數所對應的同余序列必然存在短周期性［9］。

三 元 組 隨 機 數［10，11］是 一 種 基 于 真 隨 機 熵 源［12－14］的 新 穎的隨機數，具有良好的統計特性，將其使用于文件加密、圖像加密和文件傳輸中，得到了較好的實際應用效果并取得了國家專利［15，16］。將三元組隨機數序列引入擴頻通信，以此為基礎，經同態均勻映射或正交變換進行改進［17－19］，得到同態三元組擴頻碼或正交三元組擴頻碼。以m 序列、分段Logistic序列［20］和線性同余序列為例，與正交三元組擴頻碼和同態三元組擴頻碼參與仿真，在蒙特卡羅直接擴頻通信模型［21］和直接序列碼分多址系統DS－CDMA［22，23］中計算誤碼率。實驗結果表明，同態三元組擴頻碼在不同幅度的正弦干擾下的誤碼率很小，正交三元組擴頻碼可以承載的用戶數更多。同態三元組擴頻碼和正交三元組擴頻碼可以降低通信系統的誤碼率，提高可靠性。

1 三元組隨機數序列

三元組隨機數將傳統的二元結構KS＝ （m，IV）擴展為由生成算法、初值和背景空間構成的三元結構KS＝ （m，IV，Key），使每次使用都會產生不同的序列。其中m 為生成算法，IV 為初始參數，Key 為用戶選擇的背景空間。該三元組隨機數序列由真隨機熵源提供初始值，以多輪重構技術構造背景，通過周期性變軌、控制空間映射和約束判斷等方法實現離散軌跡變換產生的。

1.1 重構背景信息

三元組隨機數序列又稱為基于廣義信息域離散軌跡變換的隨機數序列。廣義信息域是所有可以表示為二進制編碼的數據所構成的空間GI，所以三元組隨機序列以用戶選擇廣義信息域的信息為熵源，通過多輪重構消除對熵源內容和大小上的依賴，得到滿足一定規模且編碼出現次數均勻的數據空間——背景BG。

Key＝ （GI，M，L，D）為用戶選擇的秘鑰空間。用重構初始位置M （mi∈Z＋）、重構長度L （li∈Z＋）對用戶選擇的廣義信息GI （記為PB0）經過S 輪重構生成PBS，即BG （背景）。計數器向量c （c0，c1，…，c255）中ck是記錄每次重構過程中編碼k∈ ｛0，1，…，255｝（k 是8位的二進制數）出現的次數。j是每輪重構的長度，所以每輪重構前ck、j要初始化為零。為使生成的數據空間具有較好的統計分布特性，設置約束參數q （默認值為10），而使PBi中所有字節編碼的出現次數相當。q越小，PBi中編碼分布越均勻，約束條件越強。通過重構約束向量c與q 比較，使背景中所有字節編碼的出現次數相當，具有良好的統計分布特性。

重構生成PBi（bi0，bi1，…，bili）的產生過程：

步驟1 每輪的重構長度j、計數器向量c初始化為0。

步驟2 PBi－1中 的 第 （mi＋j）modli－1項 記 為bi－1（mi＋j）modli－1，并將其循環左移 （mi＋j）／li－1位，得到bj′。

步驟3 用cmin記錄c 中最小的值，記錄c中bj′出現的頻次為cbj′。若cbj′－cmin＜q，則令PBi的第j 位bij＝bj′；若cbj′－cmin≥q，則令bij＝｛k｜ck＝cmin｝。

步驟4 cbij＝cbij＋1，j＝j＋1。

步驟5 當j與本輪重構長度li相等時，則結束該輪重構。否則，返回步驟2。

1.2 三元組隨機數序列生成過程

IV＝ （t，v，u）為初始隨機動態因子。t、v 由系統生成，分別為系統時間戳和系統隨機數，u 為用戶輸入的初始個性化信息。可見，每次生成的不重復隨機的初始點由IV 決定，也是每次生成不同三元組隨機序列的關鍵決定因素。軌跡變換參數D（d0，d1，…，dm－1）構造地址映射函數，定義了邏輯地址的最大值。設每次析出w bit數據，則Ck′是計數器向量C′（C0′，C1′，…，C2w－1′）中記錄生成隨機數序列過程中編碼k∈ ｛0，1，…，2w－1｝出現的次數，即C′要初始化為零向量。設置軌跡變換參數q′ （默認值為10），利用C′與q′的比較，避免了小周期的存在，而且增加了平衡度，實現了約束判斷。

生成三元組隨機數的過程：

步驟1 初始計數器向量C′為零向量。將由用戶的任意輸入初始信息u、系統時間戳t、系統隨機數r構成初始隨機動態因子IV，經hash函數單向映射為一個長度為32×m bit的二進制字符串，并分割為 ［32×m］的向量組，定義為泛空間地址AI（x0，x1，…，xm－1）。

步驟2 AI經軌跡變換地址D（d0，d1，…，dm－1）模約束 后，得 到 邏 輯 地 址A（a0，a1，…，am－1），其 中ai＝ximoddi。

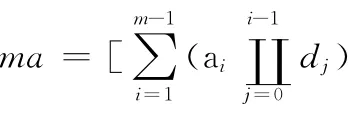
步驟4 從的第ma 位順序析出w bit二進制數，記為M。若CM′－Cmin′＜q′，M 加入隨機序列KS。若不滿足，則ma＝ma＋1，重復步驟4。

步驟5 當KS為64的整數倍時，｛k｜Ck′＝Cmin′｝替換M 加入背景BG。

步驟6 若KS的長度達到要求，則停止。否則，將AI邏輯左移M，更新AI，返回步驟2，實現周期變軌。

2 三元組擴頻碼

通過2種方案對三元組隨機序列進行改進，使三元組隨機數序列具有更好的自相關和互相關等隨機統計特性，滿足擴頻通信的使用，并使三元組擴頻碼適用于不同的使用環境。

2.1 三元組擴頻碼構造

方法一是將三元組隨機數序列KS 經過均勻映射，變為同態三元組擴頻碼KC，使三元組隨機數序列軌道和獲得同態三元組擴頻碼的軌道可以相互拓撲等價，同態三元組擴頻碼KC 具有更強的隨機性，來保證三元組系統最大的動態性。同態三元組擴頻碼KC 有優良的平衡度，可以增強系統的載波抑制度。

將二值三元組隨機數按順序析出n bit，變為一個十進制數，得到序列xn＝ ｛x0，x1，x2…｝，即若KS 的長度為L，則序列 ｛xn｝的長度為L－n＋1。均勻映射g （·）定義為

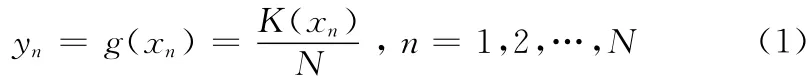
式中：N—— ｛xn｝的長度，K（xn）——xn在 ｛xn｝中按升序排列的序號。將實值序列轉換為二值序列，引入轉換函數為

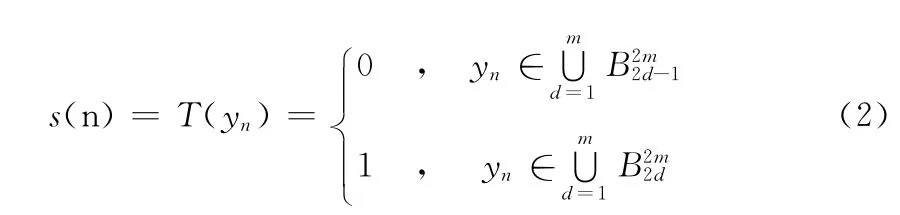
式中：2 m——正整數，B2m0，B2m1，B2m2，…，B2m2m——在 ［0，1］上連續相等的2 m 個子區間。s（n）——同態三元組擴頻碼KC。

方法二是利用正交變換具有可以去除信號中的相關性和讓信號能量集中的功能，通過正交變換使三元組隨機數序列KS變為正交三元組擴頻碼KQ，可以使正交三元組擴頻碼具有更好的互相關特性。

m 序列通過模2 加變為Gold序列，在Gold序列后加一位0或1變為正交Gold序列，而正交Gold序列具有良好的自相關性和互相關性。同理，我們利用此方法使2個三元組隨機數序列變為一個正交三元組擴頻碼KQ，使正交三元組擴頻碼KQ 具有良好的統計特性。若三元組隨機數序列KS 的長度為L，則正交三元組擴頻碼KQ 的長度為L＋1。

正交三元組擴頻碼KQ 的生成，如圖1所示。

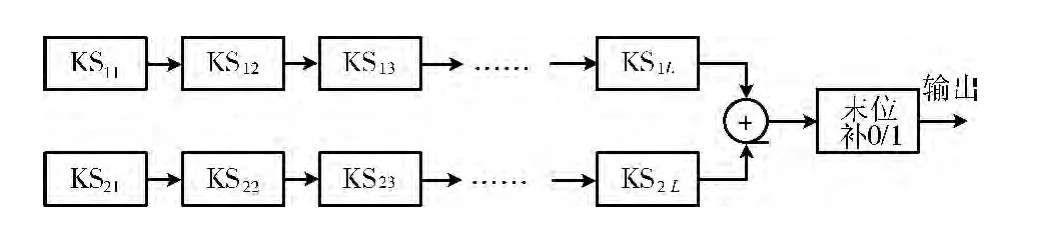
圖1 正交三元組擴頻碼KQ 的生成

2.2 三元組擴頻碼的性質

三元組擴頻碼通過C′與q′的比較和當序列長度為64整數倍時更改當前編碼等周期性變軌控制，使序列具有周期不重復性。

引入基于用戶U 盤、手機和計算機等電子設備中存儲的數字信息的廣義信息域，作為三元組擴頻碼的熵源空間，使得隨機序列具有了真隨機性，更不可預測。即使用戶的輸入初始信息相同，與系統自動生成的隨機數和系統時間戳經hash函數共同映射后，得到的初始參數也會不同，并通過反饋迭代機制，可輸出大量完全不相關的序列，具有初值敏感性。

由于三元組擴頻碼對初始條件極為敏感，2 個幾乎相同的系統，即使處于完全相同的用戶初始值也會迅速變為完全不同的狀態。同時增加了系統的抗碰撞性，消除了用戶輸入初始值的重復性或相似性的影響。

周期性變軌、控制空間映射和約束判斷等方法的離散軌跡變換，使三元組擴頻碼的算法具有隨機性。相比于混沌序列只有初值具有隨機性，使產生的三元組擴頻碼具有更強的隨機性。

經驗證三元組擴頻碼具有良好的初值敏感性、周期不重復性、平衡度、混沌特性、抗碰撞性和強隨機性，通過了嚴格的NIST SP800－22隨機性測試，且其產生速度可以滿足實際中應用的需要。

經同態均勻映射得到的同態三元組擴頻碼，有很強的載波抑制度，可以在通信系統中抵抗較強的噪聲干擾。正交三元組擴頻碼經正交變換而有更好的自互相關性，具有較強的抗碼間多址干擾特性，適合擴頻通信多用戶使用。

2.3 擴頻碼的性能分析

常用的擴頻碼以Logistic序列為例，與同態三元組擴頻碼KC 和正交三元組擴頻碼KQ 分析比較其性能，驗證了三元組擴頻碼適合用于擴頻通信系統。

2.3.1 平衡性分析

平衡度測試是隨機性測試中非常重要的環節，擴頻碼的平衡性與系統的載波抑制度有關。若不平衡，則通信系統的載波泄漏變大，降低系統性能。平衡度E 的定義為

式中：L——序列的長度，P、Q——序列中1 和0 的總個數。E 值越小，平衡度越好，則該序列的性能越好。

由圖2分析同態三元組擴頻碼KC 和正交三元組擴頻碼KQ 的平衡度優于Logistic的，且受序列長度影響較大，序列的長度越長，序列平衡性越好。經仿真得，當同態三元組擴頻碼KC 的長度為偶數時，其平衡度等于析出位數n；而長度為奇數時，其平衡度等于2n－1，所以同態三元組擴頻碼KC 具有非常良好的平衡性。

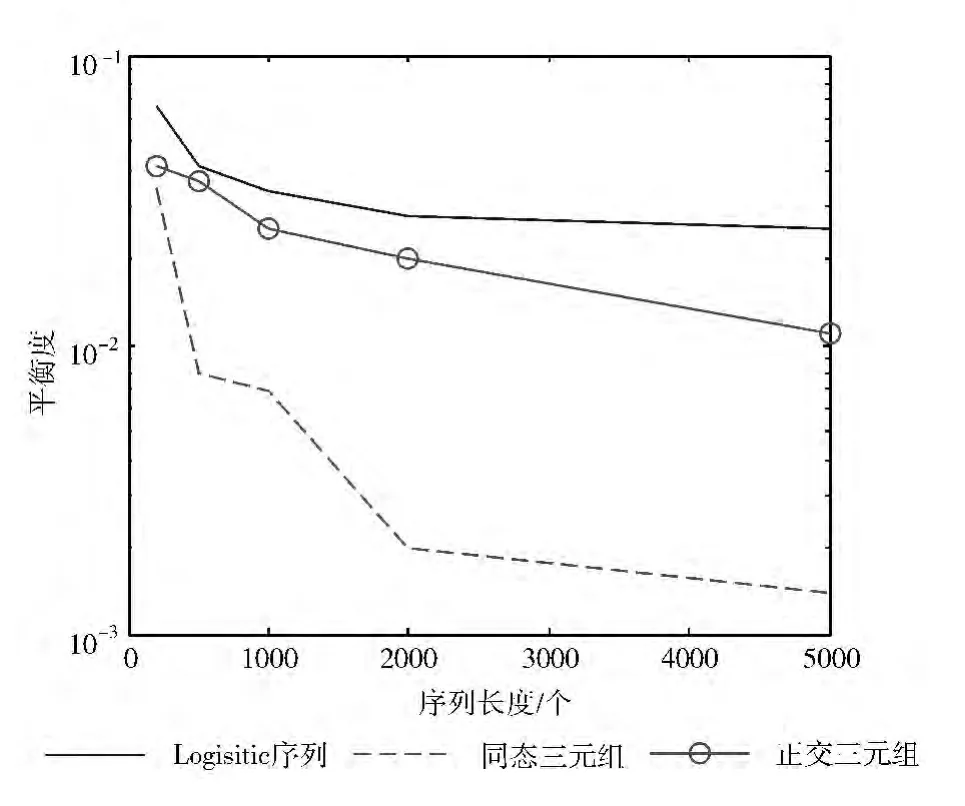
圖2 擴頻序列的平衡度

2.3.2 相關性分析

在擴頻通信系統中，良好的序列相關性是選擇擴頻碼的關鍵，包括自相關、互相關和部分相關。自相關性能好便于檢測，例如接收端的捕獲和跟蹤；互相關性能好，可減少碼間串擾，實現更多用戶的使用，即多址通信。

圖3、圖4是同態三元組擴頻碼KC 和正交三元組擴頻碼KQ 的相關性，驗證了其具有同傳統擴頻碼一樣的良好的相關統計特性。統計不同長度的Logistic序列與同態三元組擴頻碼KC 和正交三元組擴頻碼KQ 的互相關均方差和平均最大互相關值，見表1和表2。遞增序列長度，擴頻序列的互相關均方差和平均最大互相關值遞減。同態三元組擴頻碼KC 和正交三元組擴頻碼KQ 的互相關均方差與Logistic序列的相差不大，但平均最大互相關值上，正交三元組擴頻碼KQ 要優于Logistic序列，同態三元組擴頻碼KC的略差。

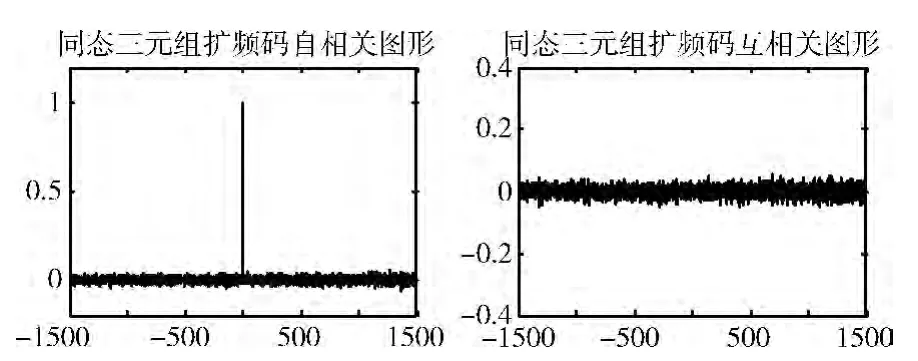
圖3 同態三元組擴頻碼KC 的相關性

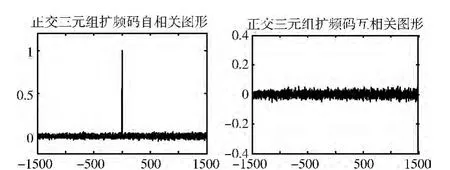
圖4 正交三元組擴頻碼KQ 的相關性

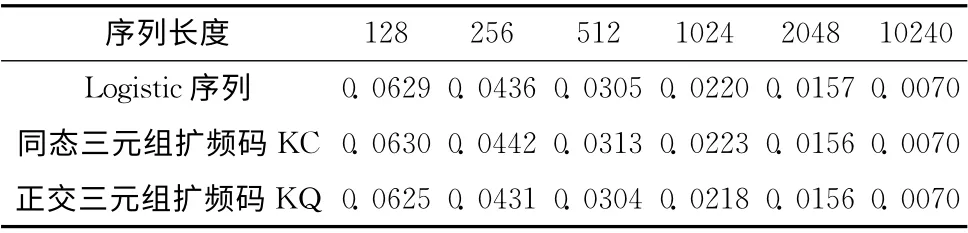
表1 擴頻序列的互相關均方差 （歸一化）

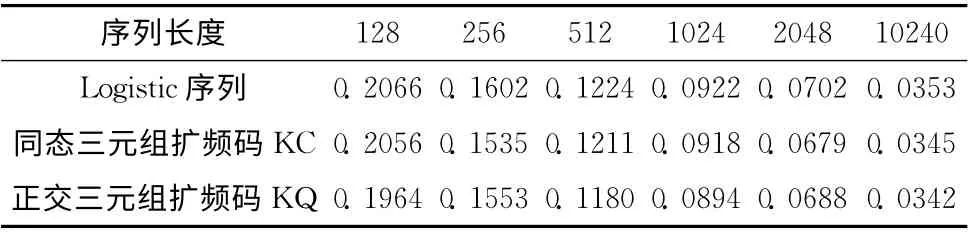
表2 擴頻序列的平均最大互相關值 （歸一化）

2.3.3 Lyapunov指數測試

Lyapunuv指數的正、負，被用來描述相鄰離散點之間經系統多次迭代后所引起的離散或靠攏情況，即Lyapunuv指數大于0，是判斷序列具有混沌性的一項依據。

選擇兩張不同的照片的任意1000個像素值作為廣義信息，經過一輪重構，仿真中變換不同的參數組合，計算同態三元組擴頻碼和正交三元組擴頻碼的Lyapunuv指數見表3和表4。得到的Lyapunuv指數均為正，表明同態三元組擴頻碼KC 和正交三元組擴頻碼KQ 都具有混沌特性。

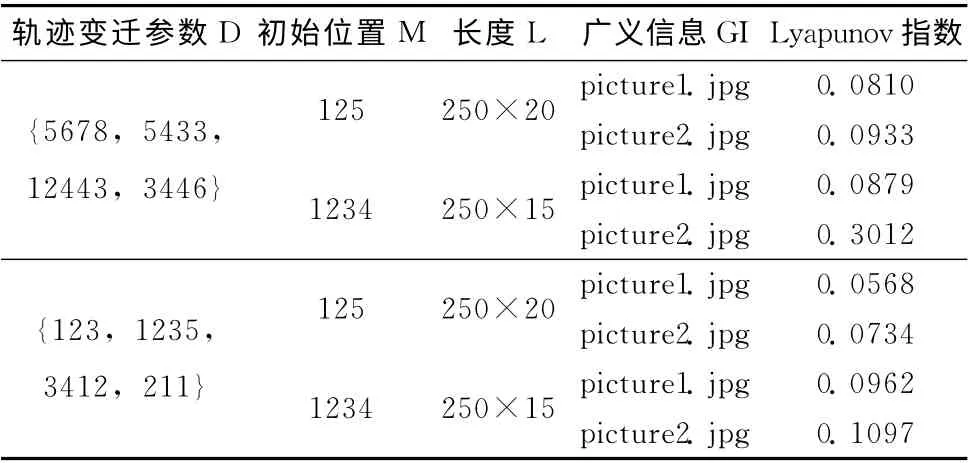
表3 同態三元組擴頻碼KC 的Lyapunuv指數

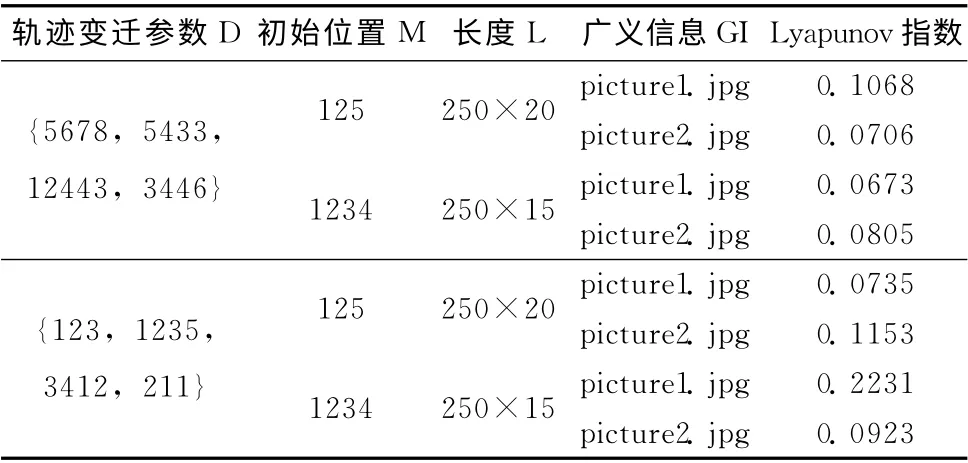
表4 正交三元組擴頻碼KQ 的Lyapunuv指數

綜上，同態三元組擴頻碼和正交三元組擴頻碼與Lo－gistic序列相比，具有良好的平衡度、自相關、互相關和混沌特性，滿足擴頻通信的基本需要。且相比于混沌序列算法缺乏隨機性，本文提出的三元組擴頻碼不僅在初始值和算法參數變化具有隨機性，而且算法本身也具有很強的隨機性，更合適應用于保密通信中。

3 擴頻碼的誤碼率分析與仿真

為檢驗同態三元組擴頻碼KC 和正交三元組擴頻碼KQ作為擴頻碼對擴頻通信系統可靠性的提高，本文以降低誤碼率為準，使用三元組擴頻碼與傳統擴頻碼進行對比。為多方面的檢驗，選用m 線性移位寄存器序列、分段Logis－tic混沌序列和線性同余序列作為傳統擴頻碼參與仿真實驗。

3.1 擴頻碼抗干擾性的仿真

使用同態三元組擴頻碼KC 與傳統擴頻碼在蒙特卡羅直擴擴頻通信模型中，在不同大小信噪比和不同幅度的正弦干擾下，仿真比較誤碼率的大小。在不同信噪比下，信號經擴頻后發送，在信道中疊加方差為σ2＝N0／2的高斯白噪聲和形式為i（n）＝Asinω0n 的正弦干擾，其中0＜ω0＜π，且仿真中令A＝0，3，7，12。接收后經解調解擴后進行輸出判決，判決后的輸出序列與原輸入信號對比，計算誤碼率。為消除偶然性，取100 次的結果求平均，如圖5所示。

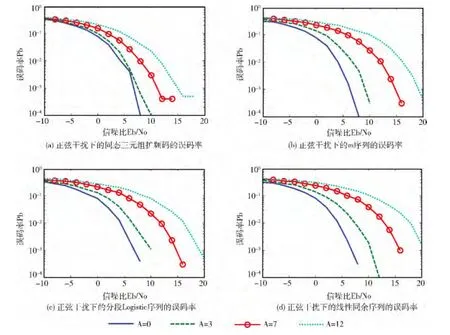
圖5 不同幅度正弦干擾下擴頻序列的誤碼率

由圖5分析可知，隨著信噪比的提高，所有擴頻碼在擴頻通信系統中的誤碼率均降低；在增大正弦干擾幅度下，相同擴頻碼的通信系統的誤碼率有所增加。在正弦干擾幅度為零時，即只有高斯白噪聲的情況下，4種擴頻碼的誤碼率相當。在相同信噪比和相同幅度的正弦干擾下，同態三元組擴頻碼的誤碼率是最低的，并隨著信噪比的提高，誤碼率保持相對快速、平穩的下降，明顯優于其它3種序列。且隨著正弦幅度增加，同態三元組擴頻碼對誤碼率降低的改善越為明顯。綜上，同態三元組擴頻碼應用在擴頻通信系統，在不同幅度的正弦干擾、不同大小的信噪比下，甚至信號被噪聲淹沒時，都能保證其很低的誤碼率和通信系統的可靠性。

3.2 擴頻碼抗碼間串擾性的仿真

在不同信噪比下，將同態三元組擴頻碼KC、正交三元組擴頻碼KQ 與傳統擴頻碼用于多用戶DS－CDMA 統中，比較通信系統的誤碼率，分析系統的穩定性。為消除隨機性，取100次實驗的平均結果，如圖6所示。

由圖6分析可知，相同信噪比下，隨著用戶數的增加，擴頻通信系統的誤碼率降低。當擴頻碼的長度均為63時，在不同用戶數的綜合比較后，同態三元組擴頻碼KC 對誤碼率有所改善，但正交三元組擴頻碼KQ 的誤碼率最低。即在多用戶的情況下，三元組擴頻碼的改善效果最好。由此可見，三元組擴頻碼更適合用于擴頻通信中多用戶的使用，增加帶寬的利用率和通信系統的可靠性。

4 結束語

三元組隨機數序列是一種新的隨機數序列體系，申請并被授權了國家發明專利。

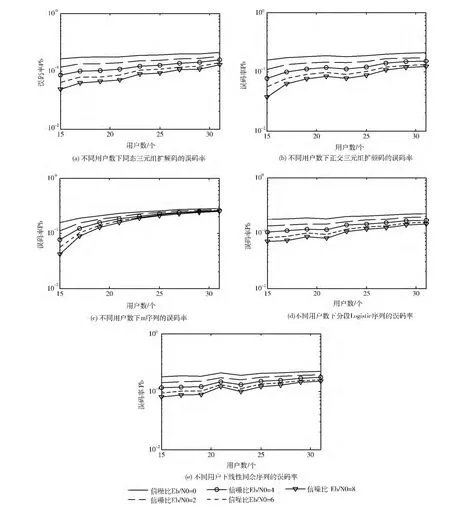
圖6 不同用戶數下擴頻序列的誤碼率

本文基于三元組隨機數序列改進，提出同態三元組擴頻碼和正交三元組擴頻碼，其是由真隨機序列發生器產生的，以真隨機熵源提供初始值，用戶選擇的廣義信息提供背景，并以多輪重構背景、周期性變軌、控制空間映射、約束判斷、同態均勻映射和正交變換等方法實現初值和算法的隨機性，具有更強的不可分析性和不可預測性，以及抗攻擊性和抗碰撞性。且三元組擴頻碼具有良好的平衡度、初值敏感性、周期不重復性、混沌特性、抗對抗性和強隨機性，統計特性更貼近于白噪聲。

同態三元組擴頻碼在較大的干擾、噪聲下，仍能保證較低的誤碼率；正交三元組擴頻碼適合多用戶的擴頻通信，抗多徑干擾性好。且其保密性好，無法從一小段構建整個擴頻碼。因此，本文所建議的三元組擴頻序列構造法為高可靠性和高安全性的擴頻系統廣泛應用提供了堅實的理論基礎。

［1］YANG LL. Multicarrier communications ［M ］. US：Wiley，2009.

［2］FazeL K，Kaiser S.Multi－carrier and spread spectrum systems：From OFDM and MC－CDMA to LTE and WiMAX ［M］.US：Wiley，2008.

［3］ZHENG DG，WANG G，LI B，et al.An improved pseudo random sequence based on the m－sequence ［C］／／Cross Strait Quad－Regional Radio Science and Wireless Technology Conference.IEEE，2011：881－884.

［4］HONG L，XU M，PENG ZZ，et al.Design and implementation of a maximal length nonlinear pseudorandom sequence［C］／／International Conference on Computer and Communications Security.IEEE，2009：64－67.

［5］Martoyo I，Susanto A，Wijianto E，et al.Chaos codes vs.orthogonal codes for CDMA ［C］／／IEEE 11th International Symposium on Spread Spectrum Techniques and Applications.IEEE，2010：189－193.

［6］YANG Q，ZHANG Y，GU X.A signal model based on combination chaotic map for noise radar［J］.Progress in Electromagnetics Research M，2013，28：57－71.

［7］ZHANG J，CHENG J，LI G.Chaotic spread－spectrum sequences using chaotic quantization ［C］／／International Symposium on Intelligent Signal Processing and Communication Systems.IEEE，2007：40－43.

［8］Dellago C，Hoover WG.Finite－precision stationary states at and away from equilibrium ［J］.Physical Review E，2000，62（5）：6275－6281.

［9］SHEN Huayun，ZHANG Peng，WANG Kan.Improved linear congruational random number gene－rators［J］.Journal Tsinghua University （Sci ＆ Tech），2009，49 （2）：191－193 （in Chinese）.［沈華韻，張鵬，王侃.改進線性同余法隨機數發生 器 ［J］.清 華 大 學 學 報 （自 然 版），2009，49 （2）：191－193.］

［10］ZHANG Guoji，LI Xuan，LIU Qing.Random number generator based on discrete trajectory transform in generalized information domain ［J］.Acta Physica Sinica，2012，61 （6）：0605021－0605029 （in Chinese）.［張國基，李璇，劉清.基于廣義信息域離散軌跡變換的隨機數生成器 ［J］.物理學報，2012，61 （6）：0605021－0605029.］

［11］LI Xuan.Research on mechanism and application of ternary key stream generator ［D］.Guangzhou：South China University of Technology，2012 （in Chinese）.［李璇.三元組密鑰流發生器的機理及應用研究［D］.廣州：華南理工大學，2012.］

［12］Marton K，Suciu A，Petricean D.A parallel unpredictable random number generator ［C］／／10th International Conference Roedunet.IEEE，2011：1－5.

［13］LI X，ZHANG G，LIAO Y.Chaos－based true random number generator using image ［C］／／International Conference on Computer Science and Service System.IEEE，2011：2145－2147.

［14］Murphy JP.Field－programmable true random number generator［J］.Electronics Letters，2012，48 （10）：565－566.

［15］ZHANG Guoji，LIU Qing，LI Fengming，et al.Dynamic streaming encryption and decryption methods in generalized information domain ［P］.China：CN 101383703B，2011－04－27 （in Chinese）.［張國基，劉清，黎鳳鳴，等.基于廣義信息域的動態流加解密方法［P］.中國：CN 101383703B，2011－04－27.］

［16］ZHANG Guoji，XU Hao，LI Fengming.System and method of advanced encryption in generalized information domain ［P］.China：CN 101394268B，2011－05－18 （in Chinese）. ［張國基，徐浩，黎鳳鳴.基于廣義信息域的高級加密系統及方法［P］.中國：CN 101394268B，2011－05－18.］

［17］WANG F L.A universal algorithm to generate preudo－random numbers based on uniform mapping as home－mophism ［J］.Chin Phys B，2010，19 （9）：0905051－0905056.

［18］RUAN Yonghong，QI Yusheng.Anti－MAI performance analysis and improvement of orthogonal code modulation in DSCDMA system ［J］.Journal of China Institute of Communications，1999，20 （8）：86－90 （in Chinese）. ［阮永紅，祁玉生.DS－CDMA 系統正交碼調制的抗多址干擾性能及其改進［J］.通信學報，1999，20 （8）：86－90.］

［19］CHEN HH，CHIU HW.Generation of perfect orthogonal complementary codes for their applications in interference－free CDMA systems［C］／／15th IEEE International Symposium on Personal，Indoor and Mobile Radio Communications.IEEE，2004：734－738.

［20］FAN Jiulun，ZHANG Xuefeng.Piecewise Logistic chaotic map and its performance analysis［J］.Acta Elecronica Sinica，2009，37 （4）：720－725 （in Chinese）.［范九倫，張雪鋒.分段Logistic混沌映射及其性能分析 ［J］.電子學報，2009，37 （4）：720－725.］

［21］Singh Pawar S，Jain A，Upadhyay R，et al.Monte Carlo simulation based error performance analysis of DS－CDMA system ［C］／／Second Asia International Conference on Modeling＆Simulation.IEEE，2008：230－233.

［22］Anichetty Murali NV，Nazeer S，Nagara Djane P，et al.Cooperative communications aided downlink DS－CDMA with transmitter preprocessing：Performance results ［C］／／Wireless and Mobile Networking Conference.IEEE，2013：1－6.

［23］ZHANG Donghong.Research on linear unified model and nonlinear improved algorithm of multiuser detection for CDMA systems［D］.Xi’an：Xidian University，2010 （in Chinese）.［張東紅.CDMA 多用戶檢測器線性統一模型與非線性改進算法研究 ［D］.西安：西安電子科技大學，2010.］