基于信號(hào)處理的橋式起重機(jī)齒輪減速箱故障診斷
鞏 銳
(江蘇省特種設(shè)備安全監(jiān)督檢驗(yàn)研究院無錫分院,江蘇 無錫214174)
0 引言
齒輪減速器是起重機(jī)上關(guān)鍵的承載和傳動(dòng)部件,長期處于高負(fù)載、工況多變等狀態(tài)下,非常容易發(fā)生故障,造成停機(jī)事故。通常齒輪減速器故障產(chǎn)生的特征信號(hào)都比較微弱,采用常規(guī)的信號(hào)檢測方法難以精確地診斷故障特征。因此,需要分析減速箱的運(yùn)行規(guī)律和故障類型的基本特點(diǎn),并結(jié)合先進(jìn)的故障特征放大技術(shù)和噪聲抑制技術(shù)進(jìn)行減速器故障檢測和診斷[1],這對準(zhǔn)確地判斷齒輪減速器的故障,保證橋式起重機(jī)運(yùn)行穩(wěn)定性具有重要的工程意義。
1 齒輪減速器故障特點(diǎn)及類型
橋式起重機(jī)齒輪減速器是一種典型的旋轉(zhuǎn)機(jī)械[2],發(fā)生故障時(shí),會(huì)產(chǎn)生異響和異常振動(dòng)等故障信號(hào),如表1所示。根據(jù)減速箱的振動(dòng)信號(hào)的特點(diǎn),可對其故障來源進(jìn)行預(yù)先診斷。然而,對于減速箱等旋轉(zhuǎn)類機(jī)械,其故障是由于很多種因素的共同作用。此外,對旋轉(zhuǎn)傳動(dòng)類機(jī)械進(jìn)行故障檢測,一般不需要將設(shè)備整件解體,否則會(huì)導(dǎo)致再次裝配精度的降低,而且某些故障特征不明顯,需要緩慢長期觀察才能確定,這使得旋轉(zhuǎn)傳動(dòng)類機(jī)械的狀態(tài)監(jiān)測和故障診斷的難度較大。

表1 齒輪箱主要振動(dòng)及原因
1.1 齒輪軸軸承損壞
起重機(jī)的工作類型復(fù)雜多樣,減速器的正常工作時(shí)間決定了齒輪與軸承的磨損和疲勞程度,影響其使用壽命。滾動(dòng)軸承的部分失效原因?yàn)槠邳c(diǎn)蝕,主要表現(xiàn)為軸承的元件在較大沖擊動(dòng)載荷和靜載荷作用下發(fā)生塑性變形,磨粒磨損嚴(yán)重,導(dǎo)致破裂損壞,進(jìn)而會(huì)產(chǎn)生輪齒的不正常卡阻、嚙合,間接導(dǎo)致齒輪發(fā)生變形和折斷,嚴(yán)重時(shí)甚至?xí)斐蓽p速箱卡滯現(xiàn)象,軸承元件點(diǎn)蝕造成的減速箱故障容易被發(fā)現(xiàn),可通過觀察減速箱的運(yùn)轉(zhuǎn)狀況或?qū)崟r(shí)監(jiān)聽噪音進(jìn)行診斷。
1.2 齒輪精度達(dá)不到要求
齒輪由于加工精度、裝配誤差等原因的存在,在運(yùn)轉(zhuǎn)工況時(shí)會(huì)產(chǎn)生不同幅度特征的振動(dòng)。不同的原因?qū)е虏煌恼駝?dòng),目前最主要的振源為嚙合振動(dòng)。齒輪在嚙入和嚙出的過程中,齒與齒之間發(fā)生周期性碰撞,從而生成振動(dòng)。除了嚙合振動(dòng),還有如制造誤差引起的損傷、外界環(huán)境引起的損傷的存在,導(dǎo)致齒廓、齒形等偏離正常范圍,增大了碰撞沖擊力度,會(huì)導(dǎo)致更大的振動(dòng)。
1.3 齒輪軸及與電機(jī)軸軸心線偏差較大
齒輪箱裝配不精確,容易造成減速箱高速軸與電機(jī)軸的軸心線偏差。偏差過大時(shí)會(huì)導(dǎo)致減速箱輪齒的嚙合出現(xiàn)故障,輪齒受力狀況不均勻,造成齒輪軸在彎曲扭矩的作用下發(fā)生變形,彎曲扭矩的重復(fù)作用和應(yīng)力集中作用會(huì)造成輪齒的過度疲勞磨損;同時(shí)也會(huì)使減速箱和電機(jī)的連接螺栓松動(dòng)變形,造成電機(jī)在運(yùn)行中振幅過大,增大減速箱的輪齒嚙合縫隙,輪齒的連續(xù)沖擊載荷導(dǎo)致輪齒變形折斷。
2 基于信號(hào)處理的齒輪減速箱故障診斷
橋式起重機(jī)齒輪減速箱發(fā)生故障時(shí),會(huì)產(chǎn)生異響、異常振動(dòng)和噪音,利用信號(hào)處理技術(shù)分析振動(dòng)信號(hào)的時(shí)域、頻域或幅值域等信號(hào)特征,進(jìn)而判別齒輪減速箱的工作運(yùn)行狀態(tài),可檢測出故障部位及其原因。
2.1 傳統(tǒng)信號(hào)處理方法
以往主要采用時(shí)域和頻域分析這兩種信號(hào)處理技術(shù)來進(jìn)行齒輪減速器故障診斷。前者主要是采用時(shí)域同步平均法、相關(guān)函數(shù)診斷法或概率分析法,分析振動(dòng)時(shí)產(chǎn)生的時(shí)域信號(hào)特征,如振幅、相位、振動(dòng)頻率、偏度、峭度、裕度等。后者則是基于傅立葉變換(FFT)進(jìn)行倒頻譜、包絡(luò)、頻譜等方面的分析。傳統(tǒng)的基于FFT的信號(hào)處理技術(shù)在理論和實(shí)踐中已有廣泛的應(yīng)用,但它目前僅用于較平穩(wěn)信號(hào)的分析,卻不適用于工程實(shí)踐中所測得的絕大多數(shù)非平穩(wěn)、非線性、非高斯分布的振動(dòng)信號(hào)。
2.2 非平穩(wěn)信號(hào)的分析方法
2.2.1 小波變換
繼傅立葉變換后,小波變換分析法由于具有一并提供信號(hào)的時(shí)域和頻域變化信息、“數(shù)學(xué)顯微”等特性,成為描述非平穩(wěn)性動(dòng)態(tài)信號(hào)、提取微弱信號(hào)、早期故障診斷以及分離機(jī)器零部件故障特征頻率的高效分析工具[3]。雖然小波變換在工程實(shí)踐的非平穩(wěn)信號(hào)分析中得到了較為廣泛的應(yīng)用,但其也存在缺點(diǎn):首先,小波變換是線性的,其本質(zhì)是在窗口中可調(diào)的傅立葉變換;其次,在選擇小波基和分解尺度后,會(huì)產(chǎn)生一個(gè)頻帶固定的信號(hào),其頻帶范圍僅與信號(hào)的采樣頻率有關(guān),不受信號(hào)本身影響,這就造成小波分析變換的自適應(yīng)性差,限制了其工程應(yīng)用。
2.2.2 經(jīng)驗(yàn)?zāi)B(tài)分解
Hilbert-Huang變換(HHT)分析方法將任意信號(hào)分解為內(nèi)在模態(tài)函數(shù)(IMF)——經(jīng)驗(yàn)?zāi)B(tài)分解(EMD)法,然后進(jìn)行時(shí)頻分析,其主要包括EMD法和Hilbert變換兩個(gè)過程,具體如下:(1)進(jìn)行信號(hào)平穩(wěn)化處理,并逐級分解出信號(hào)中不同尺度的波動(dòng),得到一系列具有不同特征尺度的IMF分量,進(jìn)一步分析和提取更準(zhǔn)確的原數(shù)據(jù)的特征信息;(2)通過EMD分解法得到每個(gè)IMF分量的信號(hào),再對每個(gè)單分量進(jìn)行Hilbert變換后能夠反映其真實(shí)的物理意義,由此得到的Hilbert譜能更加精確地反映出能量在空間(或時(shí)間)尺度上的分布規(guī)律。另外,EMD分解出的分量隨信號(hào)本身的變化而改變,因此,該方法具有自適應(yīng)性,可對多種非平穩(wěn)、非線性信號(hào)進(jìn)行時(shí)頻分析。
EMD方法能將非線性、非平穩(wěn)信號(hào)序列x(t)有限地分解為不同信號(hào)特征的IMF的和,IMF分量分別記為c1,c2,…,cn和殘差項(xiàng)r。其分解步驟如下:
(1)解析原始信號(hào)的所有極值點(diǎn)。
(2)將極大值點(diǎn)和極小值點(diǎn)分別連接起來,確保由極大值點(diǎn)構(gòu)成的上包絡(luò)曲線和由極小值點(diǎn)構(gòu)成的下包絡(luò)曲線要涵蓋所有的原始數(shù)據(jù)點(diǎn)。
(3)求出上、下包絡(luò)曲線的平均值m1,并求出:

(4)首先判定h1是否是IMF分量,若h1為信號(hào)x(t)的第一個(gè)IMF分量,則將其定義為c1,并直接進(jìn)入步驟(5)計(jì)算;若否,則h1作為新的原始數(shù)據(jù),并重復(fù)(1)~(4)的步驟,以此類推。
(5)將c1從x(t)中提取出來,得:

(6)重復(fù)(1)~(5)的步驟n次并得到有限n個(gè)IMF分量。即:

當(dāng)rn成為一個(gè)單調(diào)函數(shù)時(shí)就停止上述步驟。將式(2)代入式(3)可得:
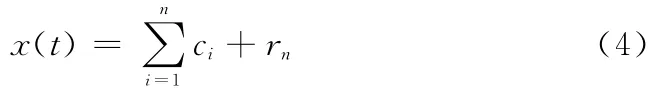
式中,rn是信號(hào)的殘余項(xiàng)。
從基函數(shù)理論來看,不同信號(hào)分解出的基函數(shù)即IMF分量c1,c2,…,cn包括了從高到低不同頻率段且是不等帶寬的信號(hào)成分,能自適應(yīng)地提取故障沖擊信號(hào),特別適用于處理非平穩(wěn)和非線性信號(hào)。
3 結(jié)語
本文針對橋式起重機(jī)齒輪減速箱運(yùn)行故障,分析主要類型及其原因,并從傳統(tǒng)信號(hào)處理技術(shù)、非平穩(wěn)信號(hào)處理技術(shù)兩方面介紹目前檢測齒輪減速箱故障的主要手段。經(jīng)分析,經(jīng)驗(yàn)?zāi)B(tài)分解(EMD)是目前檢測非平穩(wěn)、非線性信號(hào)最適用的方法。
[1]孟濤.齒輪與滾動(dòng)軸承故障的振動(dòng)分析與診斷[D].西安:西北工業(yè)大學(xué),2003.
[2]丁保華,李占芳.齒輪箱故障診斷中振動(dòng)信號(hào)處理方法綜述[J].煤礦機(jī)械,2005(8):136-138.
[3]姜洪開,王仲生,何正嘉.基于自適應(yīng)提升小波包的故障微弱信號(hào)特征早期識(shí)別[J].西北工業(yè)大學(xué)學(xué)報(bào),2008,26(1):99-103.

