中國股市長記憶性與趨勢變化研究

張金鳳+馬薇

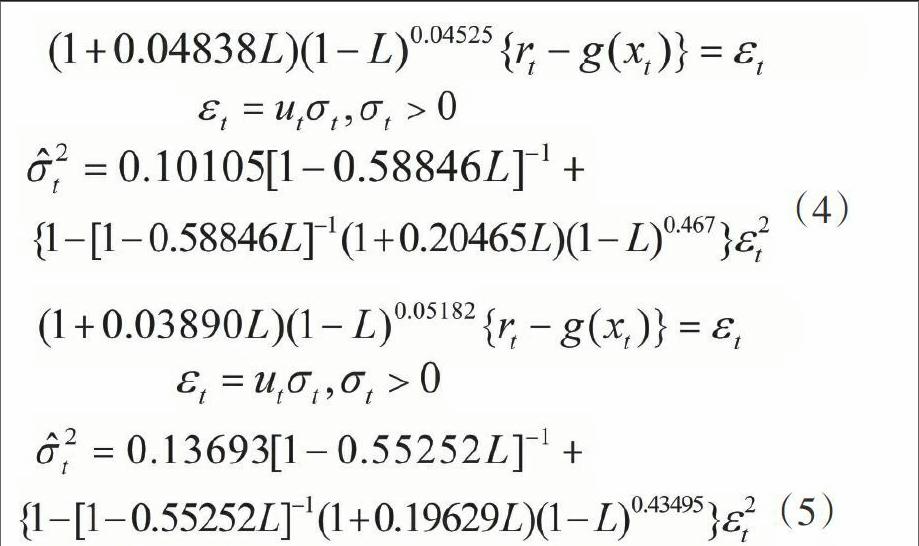
摘 要：文章對中國股市的長記憶性進行研究，在研究中將SEMIFAR模型與FIGARCH模型相結合，建立了既能反映收益率趨勢變化情況又能描述收益率和波動長記憶特征的SEMIFAR-FIGARCH模型，利用該模型對我國滬、深兩市的收益率和波動率的長記憶性及趨勢變化進行實證分析，并與ARFIMA-FIGARCH、ARFIMA-HYGARCH模型結果比較擬合及預測效果。研究結果表明：我國滬、深兩市的收益率和波動率均存在長記憶性；其收益率序列存在顯著的趨勢變化特征；SEMIFAR-FIGARCH模型的擬合和預測效果優于ARFIMA-FIGARCH、ARFIMA-HYGARCH模型，表明SEMIFAR-FIGARCH模型對我國股市有較好的模型解釋能力和預測能力。

關鍵詞：SEMIFAR-FIGARCH模型；趨勢；長記憶；核估計方法

作者簡介：張金鳳，女，天津財經大學博士研究生，天津工業大學理學院教師，從事非參數計量經濟學研究；馬薇，女，天津財經大學理學院博士生導師，從事非參數非線性計量經濟學研究。

基金項目：全國統計科學研究項目“大數據條件下金融風險測度的方法研究”，項目編號：2014LY003

中圖分類號：F830.91 文獻標識碼：A 文章編號：1000-7504（2015）06-0055-07

金融時間序列的長記憶性也稱為長期相關性，描述了金融時間序列中相距較遠的觀測值之間穩定的依存關系。Mandelbrot最早提出了長記憶性的概念，并將其應用在資產收益的研究中，此后，在金融領域長記憶性得到廣泛的應用。對金融時間序列而言，具有長記憶性意味著過去會持續影響著未來。如果金融時間序列存在長記憶性，一方面基于布朗運動和鞅過程假設所導出的金融衍生產品定價模型將失效，金融市場會面臨較大的風險；另一方面長記憶性的存在可為金融資產的預測提供一定的理論支撐。因此，關于金融時間序列長記憶性的檢驗與研究，逐漸成為近年來金融領域研究的一個熱點和重點問題，特別對金融市場的風險控制、價格預測、市場監管等方面都有著重要的理論意義與應用價值。

目前關于金融時間序列長記憶性的檢驗與研究主要有統計方法和模型方法兩大類。從20世紀80年代以來，國內外學者關于長記憶性進行了大量實證研究。Greene和Fielitz（1977）[1]，Barkoulas、Baum和Travos（2000）[2]，Sibbertson（2004）[3]通過R/S檢驗表明美國、希臘、德國等國家的股票收益率存在明顯的長記憶性；王春峰、張慶翠和李剛（2003）[4]利用R/S方法對我國1993—2001年間滬、深兩市的長記憶性進行檢驗，得出我國股票市場存在較強的長記憶性，不是一個效率市場；張維和黃興（2001）[5]檢驗出中國股市日、周收益率均存在長記憶特征，市場呈非線性的波動。在模型方法上，Granger和Joyeux（1980）[6]，Hosking（1981）[7]提出了能夠較好描述金融時間序列持續性和長記憶性的ARFIMA模型，并廣泛應用在經濟金融領域中。對金融時間序列的波動情況，目前多采用GARCH模型族如FIGARCH模型和HYGARCH模型來刻畫其長記憶性。一些學者還嘗試將ARFIMA模型與FIGARCH、HYGARCH模型分別結合，構造出ARFIMA-FIGARCH模型和ARFIMA-HYGARCH模型來同時考察金融時間序列收益率和波動的雙長期記憶程度，如Kang和Yoon（2006）[8]利用上述模型分析了日本、韓國、新加坡以及中國香港的股票市場，得出這些股市的收益率不存在長記憶性，而波動存在長記憶性和非對稱性；張衛國、胡彥梅和陳建忠（2006）[9]，曹廣喜（2009）[10]，石澤龍和程巖（2013）[11]分別對我國股市及亞洲匯率市場建立了ARFIMA-FIGARCH模型和ARFIMA-HYGARCH模型來檢驗金融市場收益率和波動率的雙長期記憶特征。此外不斷有學者對上述長記憶研究的模型方法進行改進與擴展，以達到更好地分析和預測效果。Beran和Ocker（1999）[12]對ARFIMA模型進行擴展，將模型中的常數項替換成平滑趨勢函數，進而提出了SEMIFAR（semiparametric fractional autoregressive model）模型。SEMIFAR模型在考察金融時間序列長、短記憶特征的同時，還可以通過平滑趨勢函數分析收益的趨勢變化，一般情況下，趨勢可分為確定性趨勢和隨機性趨勢兩種，因此SEMIFAR模型能較好地捕捉到任何一種趨勢的變化。隨后，Beran和Feng（2002）[13]系統地總結了SEMIFAR模型的估計方法，簡單地討論了模型的預測能力，并指出SEMIFAR模型要比一般的平穩長記憶模型更強大。Feng、Beran和Keming（2007）[14]，Chikhi、Peguin-Feissolle和Terraza（2013）[15]分別將SEMIFAR模型應用到各種實際分析如匯率、股市中，發現該模型有較強的解釋能力。國內應用SEMIFAR模型的文獻還很少，陳秋雨（2011）[16]通過SEMIFAR模型研究了中國黃金期貨市場，發現其收益率存在很強的長記憶性，并指出長記憶中大部分由確定性趨勢來把握，隨機性趨勢則接近隨機游走過程；鄭雪峰和陳銘新（2012）[17]對深圳成指1997—2011年收益率建立SEMIFAR模型，得出深圳成指收益存在長記憶性，其趨勢變化是先降再升，其后又下降的態勢，并進行了相應的預測，得到較好的結果。

通過對文獻的梳理，發現國內關于SEMIFAR模型主要集中在金融資產收益率的長記憶性與趨勢變化的研究，而同時考察收益率和波動長記憶性的SEMIFAR模型還沒有做更深入的探討。因此，本文將SEMIFAR模型與FIGARCH模型結合，構成SEMIFAR-FIGARCH模型對中國股市進行實證研究，同時為了比較模型擬合和預測效果，與ARFIMA-FIGARCH模型和ARFIMA-HYGARCH模型進行對比分析。本文通過實證分析考察SEMIFAR-FIGARCH模型在擬合數據、預測效果方面是否優于ARFIMA-FIGARCH模型和ARFIMA-HYGARCH模型，在這過程中還研究了中國股市是否存在明顯的趨勢變化情況。

一、模型設定與改進

（一）SEMIFAR-FIGARCH模型

Beran提出的SEMIFAR模型，既考慮了金融時間序列的短期和長期記憶特征，又能把隱藏在確定性趨勢背后的隨機性趨勢挖掘出來，可見，SEMIFAR模型是研究金融時間序列趨勢變化成因的一個有力工具。此外為了更好刻畫金融資產波動率的長記憶性，Baillie、Bollerslev和Mikkelsen（1996）用（1-L）s代替IGARCH模型的一階差分算子從而提出了FIGARCH模型。在實際中，金融時間序列的收益率和波動率大多存在長記憶性，因此本文將SEMIFAR模型與FIGARCH模型相結合得到SEMIFAR-FIGARCH模型，該模型不僅能同時考察金融資產收益率和波動率的長記憶性，還能刻畫收益率的趨勢變化組成情況，這是以往長記憶模型所不能提供的。

設時間序列 ，則SEMIFAR（p，δ）-FIGARCH（r，s，n）模型形式如下：

（1）

正整數m∈{0，1}，?（L）、α（L）和β（L）分別是滯后算子L的p階、r階和n階多項式。（1-L）δ的二項展開式為：

（2）

是gamma函數， 。（1-L）δ的二項展開式同（2）式。參數p描述了序列{Yt}的短期記憶程度，分整參數δ∈（-0.5，0.5）刻畫了序列{Yt}的記憶程度，當δ∈（0，0.5）時，序列{Yt}具有長記憶特征；當δ∈（-0.5，0）時，序列{Yt}具有反持續性；當δ=0時，序列{Yt}具有短期記憶性。由于許多金融資產都可通過至多一次差分實現平穩，因此正整數m的取值為0或者1，是時間序列{Yt}差分到平穩的次數，m=0時，Yt=g（xt）+ξt；m=1時，（1-L）Yt=g（xt）+ξt，顯然?（L）（1-L）δξt=εt就是一個q=0的ARFIMA（p，δ，0）過程，是一個平滑趨勢函數，刻畫序列的趨勢變化，一般采用非參數核估計法估計。波動率方程中其中w為常數項，參數s刻畫了FIGARCH過程的長期記憶特征且0

從模型的形式可以看出，由于平滑趨勢函數的引入，使得SEMIFAR模型更加靈活，應用也更廣泛。同時也注意到，SEMIFAR模型并不包含移動平均過程MA項，也就是剔除了隨機擾動項前期累計影響，充分體現了當前數據的變化特征。

（二）SEMIFAR-FIGARCH模型估計方法

為了估計SEMIFAR-FIGARCH模型中的參數，不妨令 是估計過程中SEMIFAR部分的參數向量，

是FIGARCH部分的參數向量， 、

是對應的參數估計向量，則SEMIFAR-FIGARCH模型中的參數可用三階段法估計：首先利用非參數方法估計趨勢項函數 ，然后估計SEMIFAR部分的參數向量 ，最后估計FIGARCH模型的參數向量 。

二、對我國股市長記憶性的實證研究

接下來利用上面改進的SEMIFAR-FIGARCH模型對我國股市收益率和波動率的長記憶性和趨勢變化情況進行分析與研究。

（一）變量選取與數據分析

為了更好地反映我國股市的變化特征，本文選取上證綜指和深圳成指在t日的收益率作為研究變量記作，Rti（i=1，2），這里收益率序列采用對數差分形式=100ln（Pti / Pt-1i），其中Pti（i=1，2）是滬深兩市在t日的收盤指數。根據經濟形勢變化的特點，選取數據樣本區間從1997年1月2日至2014年5月15日，各有4197個收益率數據包含了我國股市上漲、下跌以及調整的全過程。為了對SEMIFAR-FIGARCH模型和ARFIMA-FIGARCH模型、ARFIMA-HYGARCH模型的擬合及預測效果進行評價和比較，將1997年1月2日至2013年4月30日共3955個樣本數據作為上述模型的估計樣本來進行建模與分析，其余242個樣本數據用于模型預測波動性能力的評價。所有實證分析過程采用S-PLUS8.0和OxMetrics6.0軟件操作，數據來源于Wind股票交易系統。

1. 基本統計分析

表1（見下頁）列出了樣本估計期內上證綜指和深圳成指的收益率序列基本統計特征。從表1所示數據可以看到，滬、深兩市收益率均值較小，偏度均為負，同時峰度值均超過正態分布的峰度值3，表明兩市收益率都具有左偏、尖峰厚尾的特征，均不服從正態分布，這也可從J.B統計量及相應的P值得出相同的結論；單位根ADF檢驗結果表明滬、深兩市收益率均為平穩序列；兩指數的ARCH檢驗統計量在5%顯著性水平下均拒絕了序列不存在異方差的零假設，即滬、深兩市收益率序列存在著ARCH效應，適合建立GARCH模型。這點從圖1也可以看出，滬、深兩市收益率序列存在較強的波動集聚性及持續性，且波動的集聚性相似。

2. 獨立性檢驗

表2（見下頁）給出了滬、深兩市收益率的獨立性檢驗的情況：在5%的顯著性水平下，兩股指的BDS統計量均大于標準正態分布的臨界值1.96，因此拒絕滬、深股市收益率序列獨立同分布的零假設。由檢驗結果可以看出，中國股市的變化規律很難確定，股市存在相應的風險。

（二）長記憶檢驗

由于金融市場大多呈現出一定的記憶性，因此，有必要檢驗滬、深兩市收益率和波動率是否存在長記憶性。這里采取GPH譜回歸法，是由Geweke和Porter-Hudak（1983）提出的一種半參數長記憶檢驗方法。時間序列{Yt}的分整譜密度為： ，其中w是傅里葉頻數，fu（w）是相對于ut的譜密度。為了求d，對上式取對數得

（3）

在大樣本且 情況下， 。參數可用最小二乘法估計，這里U是Uj的樣本均值。GPH譜回歸法能直接給出分整參數d的估計值，而d與Hurst指數（H）之間的關系為H=d+0.5。Hurst指數包含了全部變動區間，當-0.5

綜合以上的檢驗結果，滬、深股市收益率序列是平穩的，存在ARCH效應，且收益率和波動率均存在長記憶性，具有一定的可預測性，因此對滬、深指數收益率和波動率序列采用SEMIFAR-FIGARCH模型來建模，其中均值方程為SEMIFAR模型，方差方程為FIGARCH模型。

（三）模型估計結果及分析

本文首先采用極大似然估計法對SEMIFAR模型進行估計，由于滬、深兩市的收益率序列均是平穩的，故兩指數SEMIFAR模型的差分參數m均取零，而滯后階數p則是從0到5的整數中進行選擇并根據信息準則BIC值最小來確定其取值，估計結果表明：滬、深兩市的SEMIFAR模型滯后階數p均為零即收益率不存在短期記憶特征；滬、深兩市的分整參數估計值分別為0.073和0.035，說明兩指數的收益率存在較弱的長記憶性，與前面的長記憶檢驗結果一致。

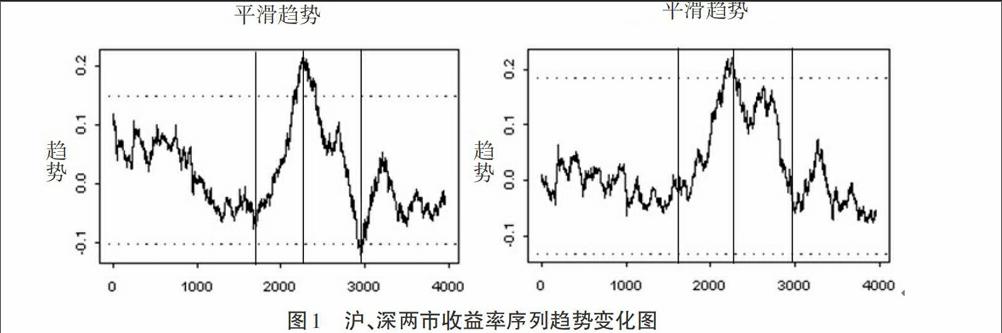
由圖1的滬、深兩市收益率序列的趨勢變化圖可以看出，上證綜指和深圳成指的趨勢變化曲線走勢大體相似，大致可分為以下四個變化階段：（1）1997年至2004年間曲線均落在置信區間內，中間有幾次較大的波動，但總體呈現出下降的變化趨勢，且上證綜指的下降趨勢較為明顯。（2）2004年至2007年間滬、深兩市的趨勢函數快速上漲，且穿過置信區間上限，均達到最大值，表明此階段確定性趨勢顯著存在。在此期間中國股市正經歷一次大的牛市，股指在短短兩年時間暴漲5倍之多。（3）2007年至2008年10月兩市的趨勢函數加速下降，其中滬指還一度接近置信區間的下限。（4）2008年11月至2014年期間滬、深兩市的趨勢函數趨于平穩，在置信區間內小幅波動。通過分析可知，利用SEMIFAR模型對中國股市收益率的階段性趨勢變化一目了然，滬、深兩市的確定性趨勢變化明顯，且兩市的長記憶性大部分可由確定性趨勢來解釋，而隨機性趨勢則帶有少部分長記憶性，這是以往研究模型不能提供的。隨著中國股市的不斷完善和健康發展，這種趨勢變化逐漸減弱。

接下來對滬、深兩市收益率和波動率序列建立SEMIFAR-FIGARCH模型，并在誤差分布分別服從正態、GED和t分布情況下，綜合考察信息準則Akaike、Schwartz、Hannan-Quinn、Shibata的估計值，得到誤差分布服從t分布時，建模效果相對較好，因此后面的研究均在誤差分布服從t分布下進行，將參數估計值代入（1）式中，從而得到上證綜指和深圳成指的SEMIFAR-FIGARCH估計模型為（4）式和（5）式：

（4）

（5）

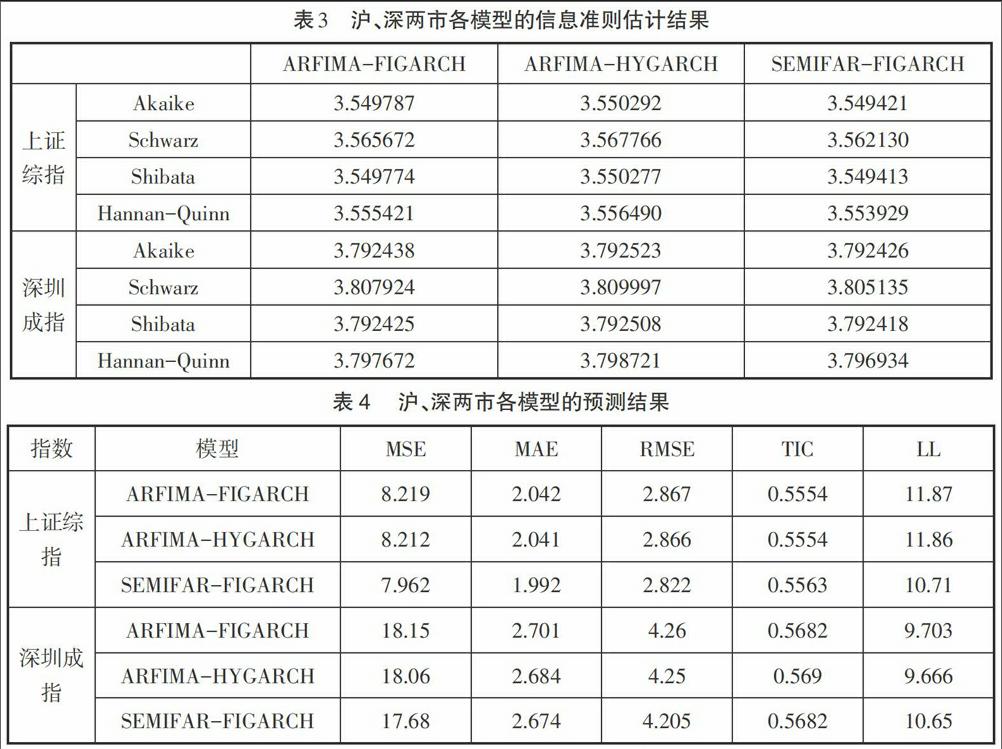
從估計模型中可以看出：滬、深兩市的收益率存在較弱的長記憶性，深市收益率的長記憶性略高于滬市，而兩市波動的長記憶性顯著存在，且滬市的波動記憶程度較高。為了對比模型擬合和預測效果，引入ARFIMA-FIGARCH模型、ARFIMA-HYGARCH模型進行比較分析，比較結果見表3：綜合四個信息準則估計值結果，滬、深兩市的SEMIFAR-FIGARCH模型的擬合效果均要好于ARFIMA-FIGARCH和ARFIMA-HYGARCH模型，表明利用SEMIFAR-FIGARCH模型對我國股市進行分析研究是適合的。

（四）模型預測結果比較

為了判斷SEMIFAR-FIGARCH模型與ARFIMA-FIGARCH、ARFIMA-HYGARCH模型對我國股市波動性的度量效果，對預留樣本數據進行預測，將滬、深兩市的收益率平方作為各自的實際波動率 ，而由模型（4）和（5）計算得出的方差 作為波動率的預測，評判標準依據下面五種預測誤差度量指標：平均平方誤差（MSE）、平均絕對誤差（MAE）、均方根誤差（RMSE）、Theil不等系數（TIC）、對數損失函數（LL），則滬、深兩市波動率的各模型預測結果見表4。

由表4的結果可以看出，在五個預測誤差度量指標中，滬、深兩市SEMIFAR-FIGARCH模型的四個指標值均小于其他兩個模型，綜合考察五個度量指標，SEMIFAR-FIGARCH模型對我國股市波動率的預測效果要優于ARFIMA-FIGARCH模型和ARFIMA-HYGARCH模型。

三、結論與展望

本文在對金融時間序列長期記憶性的模型檢驗進行整理的基礎上，將SEMIFAR模型擴展成SEMIFAR-FIGARCH模型，用于檢驗我國股市收益率和波動率的長記憶性，同時分析收益率的趨勢變化走勢，為中國股市長記憶性的研究又提供了一個有力工具。通過以上實證研究，可以得出以下結論：

（1）本文通過SEMIFAR-FIGARCH模型對我國股市的研究表明：滬、深兩市的收益率長記憶性較弱，而波動率具有較強的長記憶性，表明我國股市存在潛在的風險。隨著國家經濟結構的轉型，證監會一系列政策的出臺，將會有效地縮短股市的記憶長度，以削弱金融市場的風險。

（2）中國股市收益率趨勢變化顯著，呈階段式下降或上升，在整個樣本區間中上證綜指和深圳成指的趨勢變化走勢相似；與深圳成指相比，上證綜指的趨勢變化尤為明顯，震蕩幅度更大，并且兩市的趨勢變化大部分可由確定性趨勢來解釋，少量由隨機性趨勢來承擔，這可能與兩指數的編制以及人們對經濟的預期有關，隨著中國股市的不斷完善和健康發展，這種趨勢變化的震蕩幅度會逐漸減小。

（3）通過比較實證結果發現，SEMIFAR-FIGARCH模型不僅能較好地捕捉到金融時間序列趨勢的變化，還能有效地提高模型的預測能力，表明利用該模型對我國股市進行研究是適合的。

當然對SEMIFAR-FIGARCH模型仍需更進一步的研究：Feng和Beran將MA過程引入SEMIFAR模型中，得到了SEMIFARMA模型，顯然SEMIFARMA模型更一般化，還體現了隨機誤差的累計影響，后續可以在均值方程SEMIFARMA方面進行深入研究。

參 考 文 獻

[1] Greene， M.， Fielitz， B.， “Long-term Dependence in Common Stock Returns”， in Journal of Financial Economics， Vol.4， No.3， 1977.

[2] Barkoulas， J.T.， Baum， C.F.， Travos， N.， “Long Memory in the Greek Stock Market”， in Applied Financial Economics， Vol.10， No.2， 2000.

[3] Sibbertson， P.， “Long Memory in Volatilities of German Stock Returns”， in Empirical Economics， Vol.29， No.3， 2004.

[4] 王春峰、張慶翠、李剛：《中國股票市場收益的長期記憶性研究》，載《系統工程》2003年第1期.

[5] 張維、黃興：《滬深股市的R/S實證分析》，載《系統工程》2001年第1期.

[6] Granger， C.， Joyeux， R.， “An Introduction to Long Memory Time Series Models and Fractional Differencing”， in Journal of Time Series Analysis， Vol.1， No.1， 1980.

[7] Hosking， J.， “Fractional differencing”， in Biometrika， Vol.68， No.1， 1981.

[8] Kang， S.H.， Yoon， S-M.， “Asymmetric Long Memory Feature in the Volatility of Asian Stock Markets”，. in Asia-Pacific Journal of Financial Studies， Vol.35， No.5， 2006.

[9] 張衛國、胡彥梅、陳建忠：《中國股市收益及波動的ARFIMA-FIGARCH模型研究》，載《南方經濟》2006年第3期.

[10] 曹廣喜：《我國股市收益的雙長記性檢驗——基于VaR估計的ARFIMA-HYGARCH-skt模型》，載《數理統計與管理》2009年第1期.

[11] 石澤龍、程巖：《基于ARFIMA-HYGARCH-M-VaR模型的亞洲匯率市場均值和波動過程的雙長期記憶性測度研究》，載《經濟數學》2013年第1期.

[12] Beran， J. ，Ocker， D.， “SEMIFAR Forecasts， with Applications to Foreign Exchange Rates”， in Journal of Statistical Planning and Inference， Vol.80， No.1， 1999.

[13] Beran， J.， Feng， Y.， “Iterative plug-in Algorithms for SEMIFAR Models- definition， Convergence and Asymptotic Properties”， in Journal of Computational and Graphical Statistics， Vol. 11， No.3， 2002.

[14] Feng， Y.， Beran， J.， Keming， Y.， “Modelling Financial Time Series with SEMIFAR-GARCH Model”， in Journal of Management Mathematics， Vol.18， No.4， 2007.

[15] Chikhi， M.， Peguin-Feissolle， A.， Terraza， M.， “SEMIFARMA-HYGARCH Modeling of Dow Jones Return Persistence”， in Computational Economics， Vol.41， No.2， 2013.

[16] 陳秋雨：《中國黃金期貨市場特征及風險控制》，浙江大學博士學位論文，2011.

[17] 鄭雪峰、陳銘新：《基于SEMIFAR模型的我國股市波動率的長記憶性研究》，載《南京財經大學學報》2012年第2期.

[責任編輯 國勝鐵]