基于時間序列的膠東半島異常降水灰色預測模型

林修棟，王 娜，張瑜潔，楊 琳，劉君秀

(1．山東省石島氣象臺，山東石島264309;2．煙臺市海洋環境監測預報中心，山東煙臺264003;3．山東省煙臺市氣象局，山東煙臺264003)

氣象災害是指不利(有害)天氣或氣候對經濟(尤其農業生產)、社會(人類生命財產)等所造成災害的總和。自20世紀80年代以來，受全球氣候暖化的影響，重大氣象災害以及由氣象災害引發或衍生的其他災害對社會經濟建設、人民生命財產安全構成極大威脅，由于其致災性，極端氣候事件越來越受到社會的普遍關注［1－2］。降水多寡而引起的洪水、澇(漬)害、濕害、凌汛、凍澇、草原白害，以及大氣干旱、土壤干旱、作物生理干旱、草原黑災是最常見也是影響最大的氣象災害，而衍生的山洪、泥石流、連陰雨、干熱風、焚風、臺風、暴風雪等災害也頻繁出現［3－4］。膠東半島在氣候上屬于暖溫帶季風型大陸性氣候區，年均降水量661．0 mm，最多年降水量959．4 mm，最少年降水量418．2 mm，相差一倍有余。降水的異常對膠東半島的生態文明、社會發展有著極為顯著的影響［5－8］，加強對膠東半島地區異常降水規律的研究，可提出科學防災的對策建議，避免或減輕災害造成的影響。筆者利用膠東半島地區24個氣象觀測站1981～2010年降水資料，根據灰色系統理論及其建模原理，建立了膠東半島異常降水的灰色預測GM(1，1)模型，并對2011～2030年異常降水進行了預測和比對論證。

1 資料與方法

采用膠東半島地區煙臺、威海和青島所轄24個國家級氣象觀測站1981～2010年實測的年降水量數據;計算降水距平百分率后，利用標準化降水指數(SPI)計算方法統計24個氣象臺站的近30年年SPI指數，建立異常降水等級表，隨后建立灰色模型對未來異常降水發生趨勢進行預測。

1．1 灰色系統理論 灰色系統理論于20世紀80年代由華中理工大學鄧聚龍教授提出［9－10］。它集合了系統論、信息論、控制論和數學方法，將其觀點延伸到社會、經濟、生態等抽象系統。灰色系統理論以“部分信息已知，部分信息未知”的“小樣本”、“貧信息”不確定性系統為研究對象，主要通過對“部分”已知信息的生成、開發，提取有價值的信息，實現對系統運行行為、演化規律的正確描述和有效監控，已經成為一套解決信息不完備系統，目前有多學科多項目應用該方法進行預測。按照灰色預測的功能和特征將其分為數列預測、災變預測、拓撲預測和系統預測四類［11－13］，其中，數列預測是對系統變量的未來行為進行預測，災變預測是指通過對災變日期的研究，尋找其規律性，預測以后災變發生的時間。在此主要通過模型實現對數列預測和灰色災變的預測。

1．1．1 灰色預測模型。灰色系統理論認為一切隨機量均是在一定范圍內、一定時間段上變化的灰色量及灰色過程。對灰量數據通過一定方式處理后使其成為較有規律的時間序列數據，再建立模型。灰色系統GM(1，1)預測模型是一階、一個變量的微分方程模型，適合于對系統行為特征值大小的發展變化進行預測。該模型是將隨機數字經過生成后變為有序的數據，然后建立微分方程，尋找生成數據的規律，再將運算結果還原的一種方法［14－15］。常用的生成方式有累加生成和累減生成。

1．1．2 GM(1，1)模型。設原始序列為 X(0)={X(0)(1)，X(0)(2)，…，X(0)(n)}，累加后生成序列有 X(1)={X(1)(1)，X(1)對應的GM(1，1)模型的微分方程為其中，α為發展灰數，α 的可容區為(－2，2);μ 為內生控制灰數［16－17］。

累減還原得:

1．1．4 GM(1，1)殘差模型和模型的檢驗。在原始序列建立的GM(1，1)模型檢驗不合格時，要對建立的GM(1，1)模型進行殘差修正，即以GM(1，1)模型的殘差數列進行灰色預測。檢驗分為殘差檢驗和后驗差檢驗。殘差檢驗通過計算相對誤差，以殘差大小來判斷模型優劣。殘差計算公式為Δ(k)=X(0)(k)－)X(0)(k)，相對誤差計算公式為ε(k)=則平均殘差為模型精度為其中，ρ為小誤差概率，當ρ≤70%時模型不合格，ρ≥95%時模型優秀。后驗差檢驗通過計算殘差數列和原始數列均方差的比值來實現。

后驗差比為C=S2/S1，式中，S1為原始數列X(0)的均方差，S2為殘差數列Δ(k)的均方差，C值越小，模型越優秀。模型精度檢驗結果按文獻［18］中檢驗等級參照表劃分等級。

1．2 標準化降水指數(SPI) 不同時間、不同地區降水量變化幅度大，直接用降水量很難在不同時空尺度上相互比較，且降水分布是一種偏態分布，所以在降水分析中采用Γ分布概率來描述降水量的變化。標準化降水指數(SPI)［19］通過計算給定時間尺度內降雨量的累積概率，能夠在多個時間尺度上進行計算比較，考慮了降水服從偏態分布的實際，假設降水量服從Γ分布，再經正態標準化求得SPI值，是一種數據分析比較的方法。該研究所涉及的年SPI的計算方法與文獻［20－21］相同。

1．3 異常降水評估指標 選取降水異常強度來進行評估。某站點某時段內的降水異常強度由發生異常時的SPI值對應的異常等級來確定，當SPI＜－1．96時，異常偏少;當SPI為 －1．96～ －1．48 時，嚴重偏少;當 SPI為 －1．48 ～ －1．00時，中等偏少;當 SPI為 －1．00 ～ －0．50 時，輕微偏少;當 SPI為 －0．50～0．50 時，正常;當 SPI為 0．50 ～1．00 時，輕微偏多;當 SPI為1．00 ～1．48 時，中等偏多;當 SPI為1．48 ～1．96時，嚴重偏多;當SPI＞1．96時，異常偏多。

2 降水異常模型的建立

2．1 異常年份的確立 一般來說，表征系統行為特征的指標超過了某個閾值(臨界值)，則稱為異常［22－23］。當降水量小于或大于某一閾值時，便認為出現降水異常，模型的預測也就是對降水異常出現的年份進行預測。通過計算，得到膠東半島地區24個縣市區的近30年逐年SPI，然后建立該地區洪澇年的原始時間序列，其中1～30代表年份，即1為發生在1981年，26為發生在2007年。相應的有青島、煙臺和威海(其他地區略，下同)降水異常年的原始數據:3，6，9，12，19，20，22，26}{5，10，13，18，20，23，25，27，28}、{5，10，13，18，20，23，25，27，28}={4，5，10，17，18，25，27，28，30}。

2．2 建立模型 分別建模并求解，得到24個站的GM(1，1)灰色模型，青島、煙臺和威海的降水異常偏少和偏多灰色模型如表1所示。

表1 膠東半島異常降水年份灰色模型

2．3 模型檢驗 以青島、煙臺和威海為例，從殘差檢驗和后驗差比檢驗結果(表2)可以看到，模型均通過了殘差和后驗差比檢驗，且達到了優秀，可以用來對未來干旱年份進行預測。

2．4 未來20年的干旱年份預測 以青島、煙臺和威海為例，對2011～2030年膠東半島地區的降水異常年份進行預測，預測結果還原至序列。結果顯示(表3)，就近期看來，2014年在青島和威海、2015和2017年在煙臺，出現降水異常，表現為偏少;2013年在威海、2016年在青島和煙臺，降水異常，表現為偏多。而這與2014年膠東半島地區的干旱和2013年的降水偏多有比較好的吻合，可信度較高。

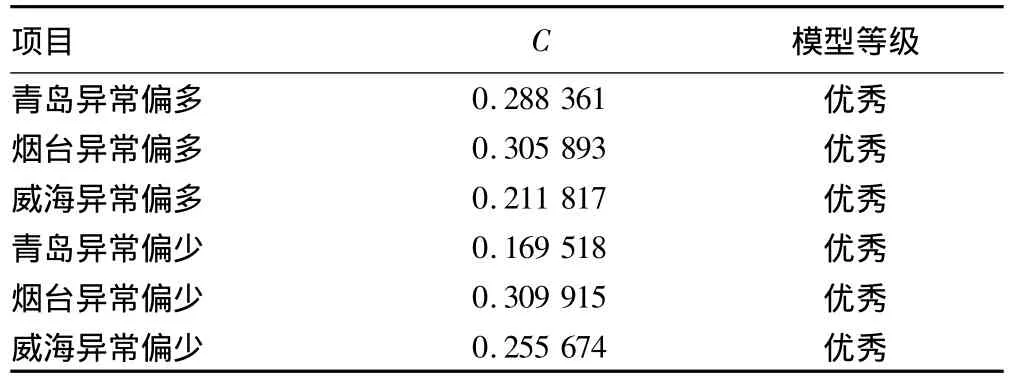
表2 膠東半島異常降水灰色模型檢驗結果

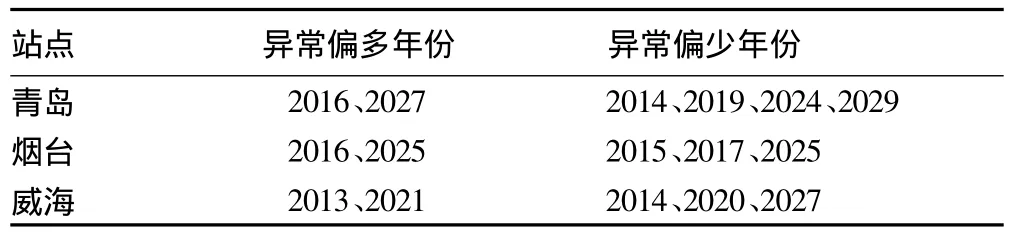
表3 2011～2030年膠東半島地區降水異常年份預測結果

3 結論

(1)通過建立膠東半島異常降水的灰色預測GM(1，1)模型，對模型進行了驗證，并對2011～2030年的異常降水進行了預測和比對論證。結果表明，2014年在青島和威海、2015和2017年在煙臺，出現降水異常，表現為偏少;2013年在威海、2016年在青島和煙臺，降水異常，表現為偏多。而這與2014年膠東半島地區的干旱和2013年的降水偏多有著比較好的吻合，可信度較高。

(2)灰色GM(1，1)模型具有要求數據較少、原理簡單、計算量適中、預測精度較高等諸多優點，但GM(1，1)適合于短序列的預測，不能用于序列中較長時間的預測，否則會產生較大的誤差。另外，原始序列本身規律的好壞也將影響預測模型的預測能力。根據灰色理論建立降水異常的預測模型過程是建立在嚴格的數學基礎上的，結果可為農業抗旱工作提供參考。

［1］周文魁．氣候變化對中國糧食生產的影響及應對策略［D］．南京:南京農業大學，2012．

［2］金文巖．氣候變暖對遼寧農業生產的影響與對策［D］．蘭州:蘭州大學，2011．

［3］劉德祥，白虎志，寧惠芳，等．氣候變暖對甘肅干旱氣象災害的影響［J］．冰川凍土，2006(5):707－712．

［4］張宏偉，林苗苗，許孟會，等．氣候變暖對河南干旱氣象災害的影響及其對策［J］．氣象與環境科學，2009(S1):239－241．

［5］王燕，衣學軍，李希國，等．膠東半島煙臺市域降水系列代表性分析［J］．水文，2002(4):50－52．

［6］劉德林，劉賢趙，魏興華，等．基于子波變換的煙臺市降水變化特征的多時間尺度研究［J］．中國農村水利水電，2007(11):68 －70，73．

［7］姜珊，于秀芹，李來民，等．1980～2010年煙臺市降水變化規律及時空分布特征分析［J］．現代農業科技，2014(3):263－265．

［8］于群，周發琇，湯子東，等．冬季山東半島局地性降水氣候的形成［J］．高原氣象，2011(3):719－726．

［9］鄧聚龍．社會經濟灰色系統的理論與方法［J］．中國社會科學，1984(6):47－60．

［10］鄧聚龍．灰色系統綜述［J］．世界科學，1983(7):1 －5．

［11］胡坤．灰色預測評價方法與應用研究［D］．南京:南京航空航天大學，2004．

［12］仇芝．灰色組合模型研究與應用［D］．南京:南京航空航天大學，2006．

［13］李曉蕾．基于灰色系統理論的變形分析與預報模型應用研究［D］．西安:長安大學，2008．

［14］張永波．基于灰色系統理論的預測模型的研究［D］．哈爾濱:哈爾濱工程大學，2005．

［15］鄧華燦，陳松林．基于灰色序列GM(1，1)模型的建設用地預測［C］//中國自然資源學會土地資源研究專業委員會．中國土地資源戰略與區域協調發展研究．中國自然資源學會土地資源研究專業委員會，2006:1．

［16］李翠鳳．灰色系統建模理論及應用［D］．杭州:浙江工商大學，2006．

［17］王換鵬．GM(1，1)模型的優化研究［D］．秦皇島:燕山大學，2012．

［18］趙君有．基于灰色理論的中長期電力負荷的預測［D］．沈陽:沈陽工業大學，2007．

［19］MCKEE T B，DOESKEN N J，KLEIST J．The relationship of drought frequency and duration to time scales［C］//Proceedings of the 8th Conference on Applied Climatology．Boston，MA:American Meteorological Society，1993:179 －183．

［20］王冰，余錦華，程志攀，等．基于SPI的煙臺地區干旱特征分析［J］．山東農業大學學報:自然科學版，2015(1):16－22．

［21］付奔，金晨曦．三種干旱指數在2009－2010年云南特大干旱中的應用比較研究［J］．人民珠江，2012(2):4－6．

［22］溫麗華．灰色系統理論及其應用［D］．哈爾濱:哈爾濱工程大學，2003．

［23］王沙燚．災害系統與災變動力學研究方法探索［D］．杭州:浙江大學，2008．