理想氣體在圓形可逆循環過程中溫度極值的討論

方 偉　涂 泓　朱炯明

(上海師范大學物理系　上海　200234)

?

理想氣體在圓形可逆循環過程中溫度極值的討論

方 偉涂 泓朱炯明

(上海師范大學物理系上海200234)

摘 要：本文討論了在p-V圖上圓形循環過程的理想氣體的溫度極值問題．結果顯示，循環過程中的最高及最低溫度和圓心坐標與圓的半徑的比值有關．當該比值a≥時，循環過程中的最高及最低溫度分別位于圓上離開原點最遠和最近的點；而當a<時，圓上會出現兩個溫度不同的極大值及兩個溫度相同的極小值，且兩個溫度極小值關于p=V直線對稱，其具體位置與a的大小有關．

關鍵詞：p-V圖溫度極值等溫線

理想氣體的壓強隨體積變化的關系，可在p-V圖上直觀表示．由理想氣體各參量所滿足的函數關系，還可以推斷出其溫度變化．在中學物理競賽或普通物理熱學課程中常常碰到這樣的試題：某理想氣體狀態的變化過程在p-V圖上是一個圓，求循環過程中的最高溫度和最低溫度各是多少．這類題目通常是通過等溫線與圓有一切點并利用一元二次方程兩根相等來求解，但是由于等溫線與圓相切的情況有時比較復雜，因此這種解法實際上是有適用范圍的．本文通過分析一道中學物理競賽題目來討論圓形可逆循環過程的溫度極值問題．

1問題的引出

1.1原題及參考解答

第15屆全國中學生物理競賽預賽第7題如下：1 mol理想氣體緩慢地經歷一個循環過程，在p-V圖中這一過程是一個橢圓，如圖1(a)所示．已知此氣體若處在與橢圓中心O點所對應的狀態時，其溫

所求出的電容值也正比于圓盤的半徑．

參 考 文 獻綜合前面的討論我們可以看出，本文開頭的競賽題給出的解法只有在a>的情況下才能成立，而[1，2]給出的競賽題相應的a分別為2和3，因而是滿足這個條件的，此解法不會出現任何問題．但若a≤，則問題會復雜一些，競賽題給出的解法不再湊效．類似的題目及結論也可在文獻[2]中找到．文獻[3]利用較為奇妙的數學技巧，更是得到氣態變化圓形圖像成立的條件，即位于直線p=V上的圓心O點的坐標值與此圓半徑R之比必須不小于，這是一個非常有趣的結論，相當于對理想氣體在p-V圖上按圓形變化的圓的大小給出了上限，若成立，應能從熱學的基本規律來解釋其背后的物理．筆者認為若該文作者在a<的情況采用本文中的圖3，則不會出現該文所認為的問題，因而是否存在這個限制條件，是值得商榷的．對于a=，由于溫度變化的一至三階導數均為零，在涉及該過程的理想氣體的一些物理量的變化是否有一些特殊性質，值得我們另文探究．

1(美)E·M·哈塞爾．伯克利物理學教程第二卷．北京：科學出版社，1979.59

2蔣衛健，胡昉，方本民．均勻帶電非導體圓盤邊緣的電勢的幾種解法．大學物理，2013，32(8)：24～28

3斯邁思W R. 靜電學與電動力學. 戴世強譯.北京: 科學出版社,1981.35～ 36,177

4熊建平．導體薄圓盤的電荷分布．大學物理，1999，18(5)：8～10

度為T0=300 K,求在整個循環過程中氣體的最高溫度T1和最低溫度T2各是多少[1]．

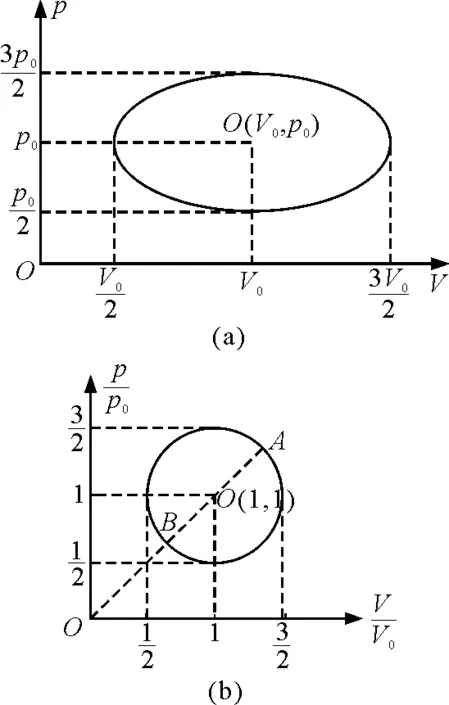
圖1　理想氣體在 p-V圖上的可逆循環，圖(a)為一般情況

下的橢圓形式，圖(b)為坐標歸一化后的圓形，方便定量研究．

此題參考解答如下：圖1(a)給出的橢圓方程為

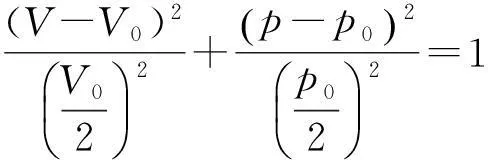
(1)

整理后可得

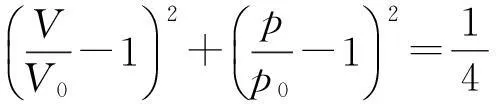
(2)

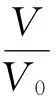
(3)

等溫線與橢圓相切時，溫度取最大或最小值，所以上式兩個根相等時溫度取極值，即

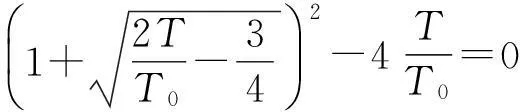
(4)

(5)

上式的兩個解則分別對應最高溫度T1與最低溫度T2

(6)

1.2極值溫度在p-V圖上的位置

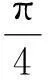
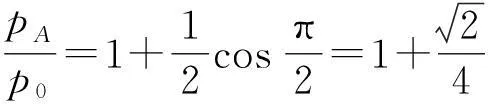
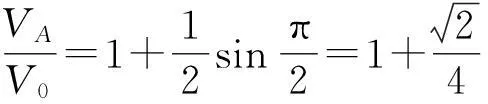
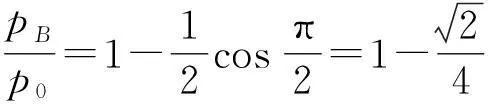
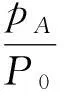
另外，從得到方程(4)的過程來看，要求兩根相等時溫度取極值，其實是認為溫度取極值時，該等溫線與圓只有一個切點，此切點對應極高或極低溫度．而從圓與等溫線均關于直線p=V對稱來看，如果按照標準答案的理解，等溫線與圓只有一個切點，那么這個切點只可能是圖1(b)中的A點或B點．

1.3一個切點假設的合理性

從以上分析可見，在解題過程中用到了一個未經證明的假設，即等溫線與圓只能有一個切點．而這一假設又直接影響到圖1(b)上的A和B兩點是否確實唯一對應變化過程在p-V圖上表現為圓形的理想氣體的最高與最低溫度．事實上，由于雙曲線和圓的斜率變化都比較復雜，因此直接使用這一假設的做法值得討論．

2等溫線與圓的切點

為研究方便，假設某理想氣體p-V關系滿足如下的圓方程

(V-a)2+(p-a)2=1

(7)

該圓圓心位于p-V圖上p=V直線上，式中的壓強p和體積V均為歸一化的無量綱變量，圓的半徑亦歸一化為1，因而此圓方程中只有一個參數，這樣的表示方便我們后面的討論，亦使得物理圖像較為清晰．根據圖2所示的等溫線和圓曲線，可以分析該理想氣體的溫度最高點和最低點．

2.1溫度最高點

圖2中A點處的等溫線曲率與圓在該點處的曲率符號相反，因此不論等溫線與圓的具體圖像如何，它們之間只能有一個交點(切點)，且為A點．再根據等溫線離原點越遠，溫度越高可知，A點確為圓上溫度最高的點．

圖2　理想氣體在 p-V圖上的圓形循環，(a,a)為圓心坐標．

θ為OP與OB的夾角，A和B為離開原點O最遠和最近

的點，過A和B兩點與圓相切的雙曲線為等溫線．

2.2溫度最低點

圖2中B點處的等溫線曲率與圓在該點處的曲率符號相同，因此存在著切點不止一個的可能性．切點坐標可由溫度對坐標的一階導數和二階導數確定．

為研究方便，取圓上任意一點P，該點與OB的夾角為θ，P從B點開始逆時針轉過一圈，則θ從零變化到2π．點P的橫縱坐標分別為

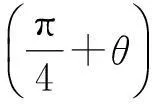
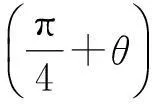
根據理想氣體狀態方程pV=νRT可知，圓上各點對應的溫度變化規律正比于P點的橫縱坐標乘積pV，因此其大小隨θ變化，即

(8)

函數T(θ)關于θ的一階和二階導數分別為

(9)

(10)

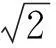
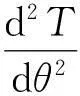
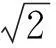
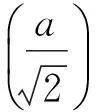
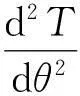
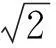
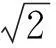
圖3　圓上溫度極值的示意圖．A，B，C，D均為等溫線與

但B點的性質稍顯特殊，因為溫度T關于θ的二階和三階導數在B點均為零，即

(11)

(12)

但溫度T關于θ的四階導數大于零，即

(13)

2.3溫度隨坐標的演化關系

圖4　a取不同值時圓上各點溫度的變化圖．B和A分別位于0

1崔宏濱編著.物理競賽真題解析(熱學·光學·近代物理學).合肥：中國科學技術大學出版社，2014.26～27

2仝響編著.物理奧林匹克競賽大題典(熱學卷).哈爾濱：哈爾濱工業大學出版社，2014.93～94

3鄭金.對氣態變化橢圓圖像成立條件的探究.物理教學， 2014(1)

4四川大學數學系高等數學教研室編，高等數學(物理類專業用，第一冊)(第三版).北京：高等教育出版社，1995.172

Discussion on Temperature Extremums of Ideal Gas

in A Circular Reversible Loop Process

Fang WeiTu HongZhu Jiongming

(Shanghai Normal University Physics Department,Shanghai200234)

Abstract:This paper discusses temperature extrema of an ideal gas which appears as a circle in a p-V diagram.The highest and lowest temperatures turn out to be dependent on the ratio between the coordinates and the radius of the circle. When this ratio a≥,the highest and lowest temperatures correspond to the two points that are furthest from and closest to the origin of coordinate,respectively.When a<,two maxima of different temperatures and two minima of same temperature appear on the circle.The locations of the two minima are symmetrical about the line p=V and depend on the value of a.

Key words:p-V diagram;temperature;extremum;isothermal curve

收稿日期：(2015-01-07)