CATIA開發環境下NURBS曲線面計算模型

陳華偉，吳祿慎，袁小翠

（南昌大學 機電工程學院，江西 南昌330031）

0 引 言

非均勻有理B樣條 （non－uniform rational B－splines，NURBS）是適用于復雜曲線面造型的建模方法，在插值計算［1，2］、創新設計［3］和高精度曲面造型［4］中得到廣泛應用。在CATIA 環境中進行曲面功能二次開發［5］，可以直接借助CATIA 成熟的顯示渲染功能，開發者只需關注功能實現；且CATIA 具有完善的應用接口 （API），支持NURBS曲面的讀取、編輯和創建，能夠將樣條曲面擬合為NURBS 曲面，并提供了自定義曲面的生成功能。

1 NURBS曲線面的參數化定義

NURBS曲線面由控制點、權因子和基函數共同表達的數學解析式定義，已知型值 （采樣）點和邊界條件，即可計算節點矢量，反求控制點陣，從而獲得解析解。

1.1 多項式定義

NURBS定義中，非均勻性 （non－uniform）指控制頂點的影響范圍可以改變，有理性 （rational）則說明NURBS曲面可以有理多項式形式定義，B 樣條 （B－spline）指曲線面的構建是通過插值實現的。

u向p 階 （次）、v向q 階NURBS曲面定義［6］為

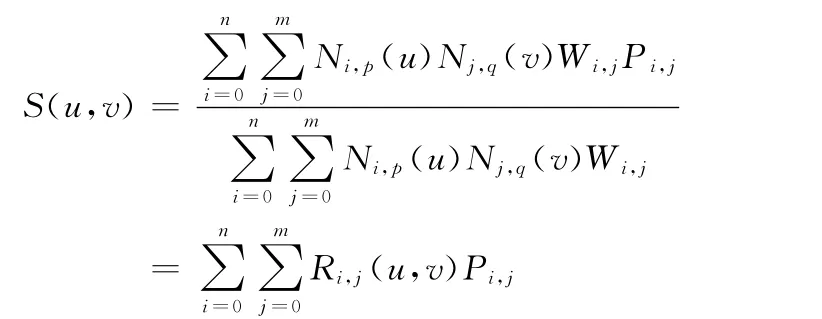
Pi，j為構成曲面控制點網，u向、v向維數分別為 （m＋1）、（n＋1）；Wi，j為權因子；Ni，p（u）、Nj，q（v）為p 階、q階B樣條基函數。

同理，k次NURBS曲線的多項式定義為

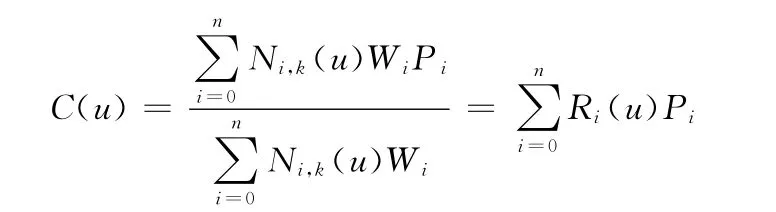
1.2 幾個重要參數

為了生成NURBS曲面，CAD 軟件都會對NURBS 曲面進行對象和參數化定義，幾個重要參數如下：

（1）自由度，階 （degree）

表示多項式的最高次數p，通常p＝1，2，3或5，用于表達一次 （Linear）、二次 （Quadratic）、三次 （Cubic）或五次 （Quintic）曲線面。

（2）控制點 （control points）

控制點的數目記為c，每個控制點均可附權重（weight），記為w。如果w 值完全相同，則成為 “非有理”（non－rational）。

（3）節點矢量 （knot）

節點矢量由一列數值組成，節點數值可以重復，重復次數稱為重復度 （multiplicity），記為m；一般記不重復節點個數為k。節點必須滿足以下兩個基本條件：

1）非減性，節點數值按非降次序排列；

2）可重復性，重復度滿足m≤p。

例：p＝3，c＝11，Knot數值依次為：0、0、0、1、2、2、2、3、7、7、9、9、9，符合以上兩項原則。但是假設Knot數值為：0、0、0、1、2、2、2、2、7、7、9、9、9，則因為有4個節點值為2，不符合原則2），因而是不合法節點矢量。

上述參數數組大小之間存在數量關系：c＝k－p－1。以三次 （p＝3）NURBS曲線插值為例，設已知型值點數目為n＋1 （i＝0，1，2，…，n），并取節點參數前后端0，1的重復個數為p，則節點數為：k＝ （n＋1）＋2×p＝n＋7，控制點數為：c＝k－p－1＝n＋3。例如，當型值點數n＋1＝6，即n＝5時，節點數k和控制點數c應分別為12和8。

以下為兩個具體實例。圖1 （a）中，擬合曲線隨著其中一個控制點CP3位置的移動 （至CP3′）而變化，并被其“吸引”；圖1 （b）中，控制點CP1－CP6不變，改變權重系數：原權重為 （1，1，1，1，1，1），新權重為 （1，1，10，20，5，1），可見曲線向權重較大的控制點CP3和CP4靠攏［7］。它們的主要參數列見表1。

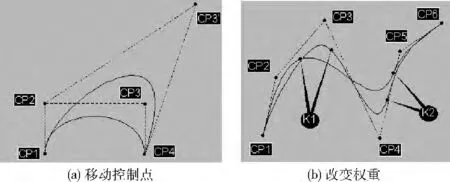
圖1 兩個實例

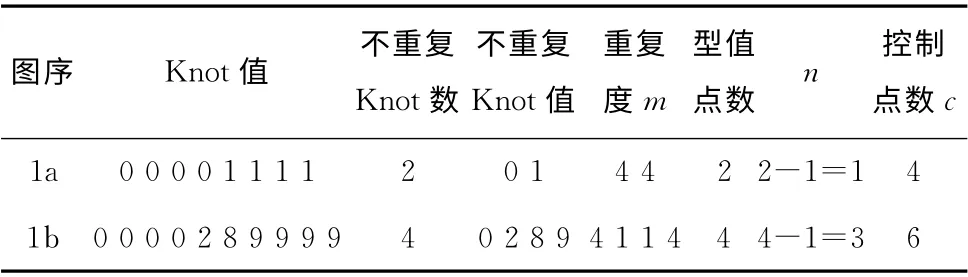
表1 NURBS曲線參數 （p＝3）

2 CATIA中曲線面對象的定義和讀取

曲面是封閉的R2至R3空間的函數，由雙變參U、V的3個標量函數FX、FY、FZ 所定義，標量函數說明了曲面參數 （U，V）到笛卡爾坐標 （X，Y，Z）的變換或映射關系。多面片曲面中每個面片中的點坐標可由局部參數（u，v）或全局參數 （U，V）定義。曲線則由單參數定義，情況類似。如圖2所示。

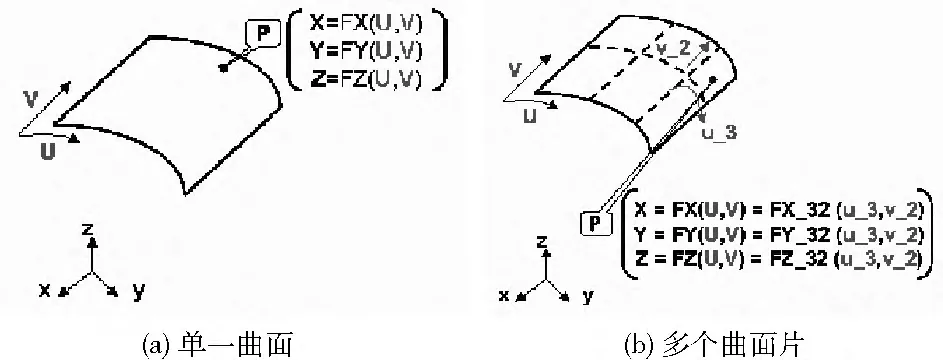
圖2 曲面的參數化定義

2.1 基本對象和接口

CATIA 幾何建模器 （CATIA geometric modeler，CGM）中封裝了CATCurve和CATSurface接口分別定義曲線和曲面對象，所定義曲線和曲面必須是二階可微，即C2連續的。與之相關聯的幾個重要對象和接口有：

（1）CATCrvParam／CATSurParam 對象：定義曲線／面上點的全局參數；

（2）CATCrvLimits／CATSurLimits對象：定義曲線／面邊界，可由包圍盒的兩個角點CATCrvParam／CATSur－Param 參數定義；

（3）CATKnotVector對象：定義節點矢量，提供了獲取節點值，控制點，分段弧數，自由度，重合度等全套接口函數；

（4）Eval接口：CATCurve／CATSurface：：Eval實現參數坐標至笛卡爾坐標的轉換和三階導數的求取；

（5）GetParam 接口：CATCurve／CATSurface：：Get－Param 實現笛卡爾坐標至參數坐標的轉換；

（6）GetEquation 接口：獲得曲線／面方程對象CATMathFunctionX／CATMathFunctionXY；

（7）GetKnotVector／GetKnotVectorU／V 接口：獲得CATKnotVector對象。

2.2 參數讀取和計算

（1）點對象信息

曲線面分別利用CATCurve和CATSurface對象的接口函數求取曲線面上的點及其導數。如曲線中點及該點切向和法向的計算過程如下：

對如圖3 （a）所示的曲線進行計算，結果為：

中點坐標：（262.734，114.157，209.558）：

一階導數：（0.779724，－0.558819，－0.358627）；

二階導數：（－0.00640612，－0.00114124，－0.00163766）；

三階導數： （－9.6987e－005，7.44916e－005，－2.68162e－005）。

可見，三階導數的取值已經非常之小，幾何意義不大。也可以采用第二種方法，即使用接口函數CATCurve：：GetEquation獲得該曲線的MathFunctionX 數學函數對象，該對象也提供了Eval類接口函數，所求結果與上述結果一致。

曲面上點信息的讀取過程與之類似，圖3 （b）顯示了曲面中點及其各向切矢和法矢的計算結果。

圖3 CATIA 中曲線的底層操作

（2）點的解析解

此外，還能讀取通過CATKnotVector：：GetPolynomialBasisForOneArc接口函數讀取NURBS多項式，并對曲線面上的點求解析解。以曲線為例：

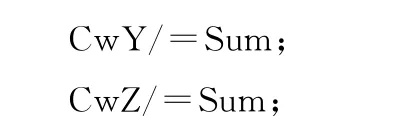
解析解計算結果與對象法讀取的結果一致。

（3）NURBS參數

為了讀取NURBS參數，應使用CATCreateCrvFitting－ToNurbsCrv全局函數 （可設置擬合誤差）將一般曲線轉化為NURBS 曲線對象CATNurbsCurve，該對象由CATCurve繼承而來，增加了GetOneControlPoint函數用于讀取控制點信息。

下面給出NURBS節點和控制點參數的讀取過程：

對如圖3 （a）所示的曲線進行計算，結果為：

自由度：5

分段弧數：3

節點數：4

節點值：0，106.771，254.757，459.452

重復度：6，3，3，6，

控制點數：12

控制點： （100，70，300） （102.004，99.0517，287.637）（108.124，121.486，276.488）

（118.362，137.304，266.554） （152.613，159.256，245.748）（203.535，148.733，229.986）

（235.575，134.094，221.656） （299.801，92.7058，198.798）（310.217，54.9492，161.893）

（286.537，43.1674，132.534） （233.131，41.5177，95.2366）（150，50，50）

將這些控制點用直線連接，結果顯示于圖3 （a）；圖3（b）中也展示了NURBS曲面參數求解后獲得的部分控制點和兩條控制線。

3 NURBS曲線面的反求

工程應用中，一般已知型值點陣Qi，j（Qi，j∈S），要求NURBS的解析表達式，因此，需要反求控制點陣P，設Q為型值點陣列，R 為基函數系數矩陣，P 為控制點網矩陣，則NURBS曲面方程定義式可表示為矩陣形式

基函數系數矩陣R 由多項式函數Ni，k（k 為階次）構成，Ni，k的基函數又由節點矢量u＝ ［u0，…，um＋2p］，v＝［v0，…，vn＋2q］采用Cox－De Boor公式［2，8］遞推

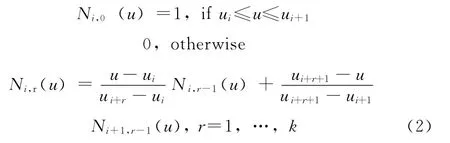
其中

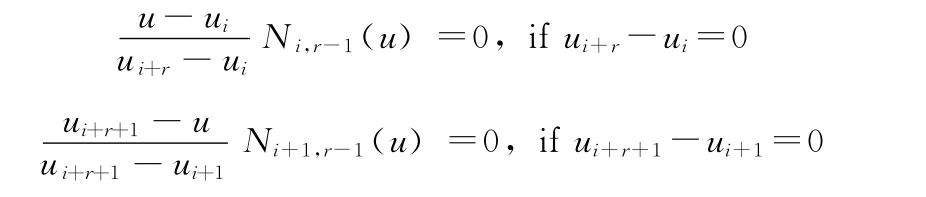
對矩陣方程進行求解，可反求出控制點：

P＝R－1Q，R 為方陣；

P＝ （RTR）－1RTQ，R 不為方陣。

NURBS曲面反求以曲線反求為基礎，而曲線反求的核心是控制點的反求，其基本步驟是：

（1）讀入型值點Q，計算節點矢量u、v；

（2）使用De－Boor公式，計算多項式基函數Ni，k，構造系數矩陣R；

（3）帶入曲線方程，構造方程組RP＝Q；

（4）附加合適的邊界條件，得到未知數個數與方程個數一致的可解方程組；

（5）采用合適的方法求解方程組，得到控制點P。

3.1 NURBS曲線的控制點反求

NURBS曲線反求可描述為：已知n個型值點Qi（i＝1，…，n），曲線自由度為k，求控制點Pi。

為滿足曲線端點就是型值點的要求，節點矢量的兩端應取k＋1重復度，即u0＝u1＝…＝uk，un＋k＝un＋k＋1＝…＝un＋2k。

對三次樣條曲線 （k＝3），取規范化節點矢量，則兩端重復節點矢量為：u0＝u1＝u2＝u3＝0，un＋3＝un＋4＝un＋5＝un＋6＝1。

首末短短重復度為m＝k＋1＝4。

其它節點值可采用累積弦長法進行參數化

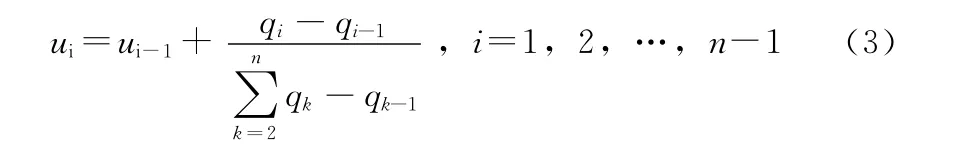
附加以下條件：

（1）首末端點應分別與控制點重合，即：p0＝q0，pn＋k－1＝qn。

（2）邊界條件。一般要求邊界點 （首末端點）切矢q0′和qn′連續，即有

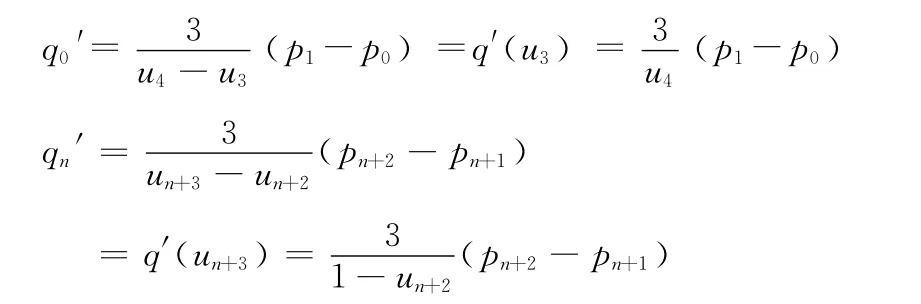
使用基函數遞推式 （2），求系數矩陣R，帶入式 （1），整理得以下矩陣方程

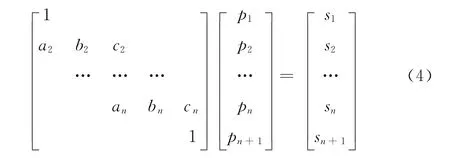
其中

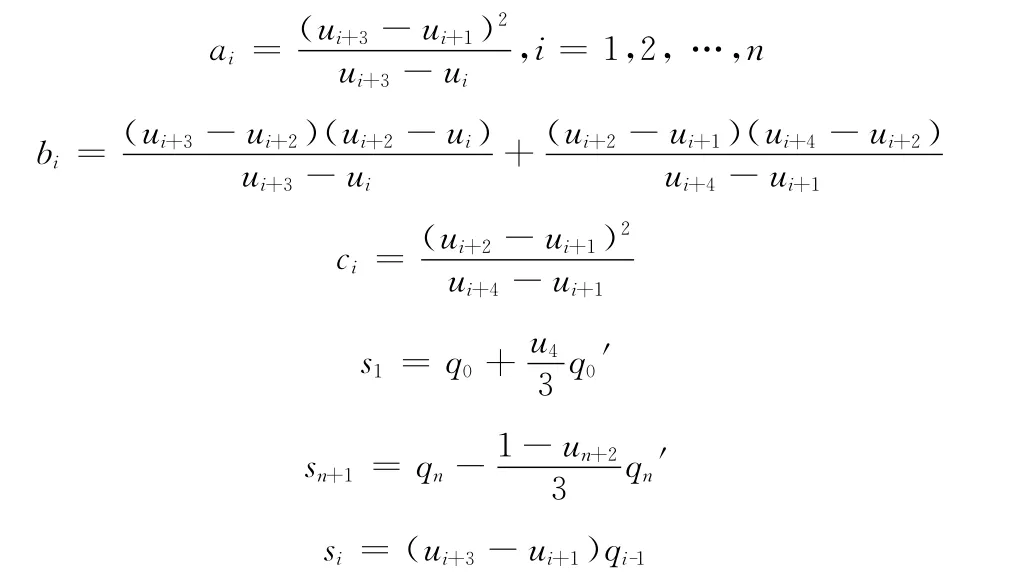
3.2 矩陣方程的求解

方程組 （1）為典型的三對角矩陣方程，易采用高斯消去法求解。

給定形的矩陣方程如下

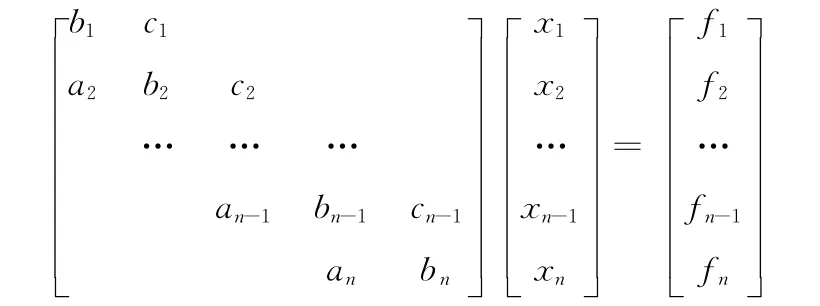
經過n－1次消元，可化為同解上三角矩陣方程

其中

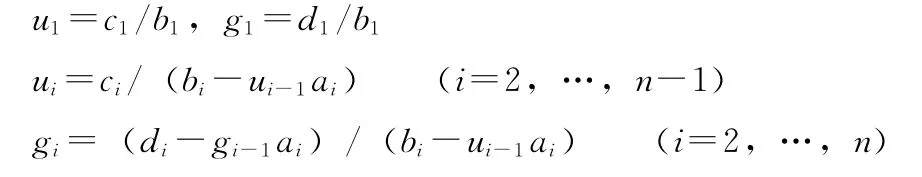
回代求出未知數：xn＝gn，xi＝qi－uixi＋1（i＝n－1，n－2，…，1）。

該過程亦稱為追趕法，是三對角方程組的典型求解方法。

3.3 m×n維點陣擬合NURBS曲面

以均勻雙三次B樣條（k＝3）為例，典型的反求問題可描述為：已知m×n維型值點陣Qi，j（i＝1，2，…，n；j＝1，2，…，m），求控制點陣Pi，j（i＝1，2，…，n＋1；j＝1，2，…，m＋1）。

采用兩次反求法，即分別對u 向和v 向控制點進行反求，即可求取控制點陣：

（1）計算u向控制點。對u 向的m 組型值點，按照反算公式，并添加邊界條件，即可求解矩陣方程，獲得m 組B樣條曲線的控制頂點Vi，j（i＝1，2，…，n，n＋1；j＝1，2，…，m）。因為每條曲線都要添加兩個邊界條件才能求解，因而每條曲線上的控制點數為 （n＋1）；

（2）計算v向控制點。將Vi，j視為v 向的m 組型值點，再作 （n＋1）次B樣條曲線反算，所求v向控制點Pi，j即為整個曲面的控制點。

CATIA 提供了幾何對象包CATGeoFactory，開放有NURBS曲線面生成的接口函數CATCreateNurbsCurve和CATCreateNurbsSurface，它們均以節點向量和控制點陣為主要輸入參數，調用結果是生成CATNurbsCurve或CATNurbsSurface對象，該對象可直接在CATIA 界面中顯示。

使用CATIA 開發環境，導入型值點陣，自定義函數封裝節點計算、控制點反求及其求解算法，然后調用CATGeoFactory：： CATCreateNurbsCurve／CATCreateNurbs－Surface接口生成NURBS 曲線面對象，轉化為特征后在CATIA 界面中顯示。圖4是在CATIA 中對30×20維點陣進行NURBS曲面重構的結果。

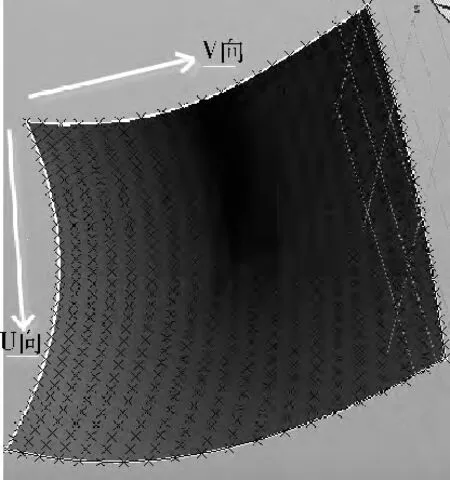
圖4 由點陣生成NURBS曲面

4 結束語

特征在界面上以對象形式存在，在底層則是通過幾何拓撲或解析計算生成。文中NURBS曲線面信息的讀取以及曲線面的反向生成，均借助CATIA 的NURBS對象接口實現，并交由顯示渲染接口生成，因而具有流程簡單，代碼清晰，可維護性和封裝性強等特點。作為曲線面建模和逆向建模的核心算法，該模塊可在復雜曲線和型面［9，10］建模分析中直接應用或修改后應用。

［1］WANG Yunsen，GAI Rongli，SUN Yilan，et al.NURBS interpolation algorithm for high－quanlity machining ［J］.Journal of Computer－Aided Design ＆ Computer Graphics，2013，25（10）：1549－1556 （in Chinese）. ［王允森，蓋榮麗，孫一蘭，等.面向高質量加工的NURBS曲線插補算法 ［J］.計算機輔助設計與圖形學報，2013，25 （10）：1549－1556.］

［2］WANG Guoxun，SHU Qilin，WANG Jun，et al.Algorithm of fast evaluation and derivation for the technique of NURBS direct interpolation ［J］.Journal of Northeastern University（Natural Science），2012，33 （7）：1021－1024 （in Chinese）.［王國勛，舒啟林，王軍，等.NURBS直接插補技術中快速求值求導算法 ［J］.東北大學學報 （自然科學版），2012，33（7）：1021－1024.］

［3］ZHOU Wei，CHENG Dewen，XU Chen，et al.Application of NURBS free－form surface in optomechanical design ［J］.Infrared and Laser Engineering，2014，43 （10）：3313－3320 （in Chinese）.［周偉，程德文，許晨，等.NURBS自由曲面在光機設計和分析中的應用 ［J］.紅外與激光工程，2014，43（10）：3313－3320.］

［4］LI Weiguo，HUANG Fengling.Application of NURBS surface reconstruction algorithm in form modification of sheets die faces［J］.Computer Applications and Software，2014，31 （10）：281－284 （in Chinese）. ［李衛國，黃風玲.NURBS曲面重構方法在板料模面修型中的應用 ［J］.計算機應用與軟件，2014，31 （10）：281－284.］

［5］WANG Liming.Three－dimensional reconstruction and parametric design of aircraft configuration based on CATIA CAA［D］.Nanjing：Nanjing University of Aeronautics and Astronautics，2014 （in Chinese）. ［王黎明.基于CATIA CAA 的飛行器參數化三維外形設計及三維重建 ［D］.南京：南京航空航天大學，2014.］

［6］Piegl L，Tiller W.Curve and surface constructions using rational B－splines［J］.Computer－Aided Design，1987，19 （9）：485－498.

［7］CHEN Jun，CUI Hanguo.Shape modification of NURBS curves based on weight［J］.Journal of Naval University of Engineering，2012，24 （4）：108－112 （in Chinese）. ［陳軍，崔漢國.基于權值的NURBS曲線形狀修改 ［J］.海軍工程大學學報，2012，24 （4）：108－112.］

［8］Carl de Boor.On calculation with B－spline［J］.Journal of Approximation Theory，1972，6 （1）：50－62.

［9］CHEN Yueping，GAO Jian，DENG Haixiang，et al.On－line inspection and machining error cmpensation for complex surfaces［J］.Journal of Mechanical Engineering，2012，48 （23）：143－151 （in Chinese）.［陳岳坪，高健，鄧海祥，等.復雜曲面零件在線檢測與誤差補償方法 ［J］.機械工程學報，2012，48（23）：143－151.］

［10］LI Yuan，WANG Yiwen，LIU Xianli，et al.Intelligent modeling of semi－open integral wheel based on nurbs［J］.Journal of Harbin University of Science and Technology，2014，19 （1）：12－15 （in Chinese）.［李媛，王義文，劉獻禮，等.基于NURBS的半開式整體葉輪智能建模 ［J］.哈爾濱理工大學學報，2014，19（1）：12－15.］