k／n（t）：（G）系統與時間相關的容量n（t）

劉春霞，何 平

（西南交通大學 數學學院，四川 成都610031）

0 引 言

為提高系統可靠性常采用冗余的方式，而冗余并非萬能，雖然能提高系統可靠性，但大量備用件會導致系統負荷過重、體積過大或者資源消耗過多等問題。目前，很多文獻提及如何配置冗余以達到效果最優［1－5］，同時也有文獻提及一些高要求設備上，并不使用冗余來提高系統可靠性。

k／n： （G）系統作為一種冗余系統，同樣存在上述問題，該系統的研究也為國內外可靠性數學領域的熱門內容。目前k／n：（G）系統的可靠性計算是可靠性領域的一個NP難題，因此對該系統的研究存在很多方面的困擾，特別是涉及該系統的維修問題。文獻 ［6］建立了隨機載荷作用下失效相關的動態可靠性模型，對k／n 系統可靠度和失效率隨時間的變化規律進行了研究；文獻 ［7］基于部件壽命服從指數分布的基礎上對表決系統可靠度進行了分析；文獻［8］利用Monte carlo隨機抽樣技術，對系統可靠性評估指標進行了模擬計算；文獻 ［9，10］對k／n：（G）系統的維修策略進行了部分研究，但由于大容量表決系統的可靠性計算困難，大量的研究都基于系統小容量或者基于部件壽命服從指數分布的假設下，對由消耗型部件組成的k／n：（G）系統的可靠性以及選擇何種容量的k／n： （G）系統甚至該情況下的維修策略研究較少。

基于上述背景，本文考慮一種由消耗型部件組成的表決系統，在系統最小工作數k 固定的情況下，根據系統期望的運行時間，對系統與時間相關的容量進行了分析。在此基礎上，考慮讓k／n： （G）系統以逐步增加部件的方式運行，嚴格推導了該方式下系統可靠性的計算公式，設計迭代算法，解決系統可靠性計算的難點。對比一次性選定的系統與逐步增加部件的系統部件使用量大小，得出逐步增加部件的方法平均每1～2天增加一個部件，時間間隔夠長，且能夠明顯減少部件的投入使用量，從而節約大量資源。

1 預備知識

1.1 符號說明

k／n（t）：（G）系統表示由n（t）中取k系統，其中n（t）視情而定；

n（t）表示k／n（t）：（G）系統t時刻的系統容量；

Pt為可靠性閾值，當系統可靠性大于閾值則系統工作，否則失效。

1.2 k／n：（G）系統

k／n：（G）系統是指一個具有n個部件組成的系統，當n個部件中有k 個或者k 以上的部件工作，系統則正常工作，否則系統失效。其中n為系統容量，k為系統工作的最小工作部件數。k／n：（G）系統的可靠性框架如圖1所示。

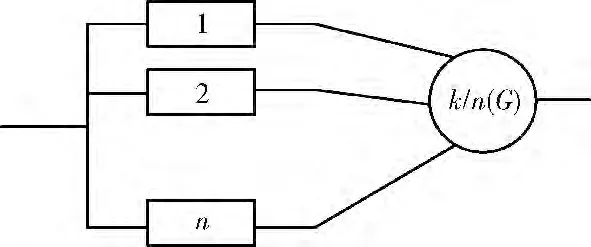
圖1 k／n：（G）系統

若k／n：（G）系統中的n 個部件獨立同分布于F（t），且記初始時刻部件為新，則系統的可靠度R（t）與時間的關系為

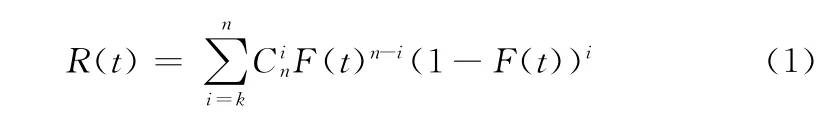
式 （1）顯示了當k 固定時，在同一時刻t，系統的可靠性會隨著系統容量的增加而增加。

2 k／n（t）：（G）系統系統容量n（t）的選擇

在系統工作要求的條件下，可以根據期望的運行時間，選擇某種容量的k／n（t）：（G）系統。很明顯，如果對系統期望的運行時間不長，系統容量就會很小，反之很大。如果根據對系統期望的運行時間而事先選擇某種容量的k／n（t）：（G）系統，由于部件一開始全部投入使用，部件熱備冗余導致部件壽命過早衰減，浪費了資源以及部件的可靠性，以這種方式選擇系統容量理論上并不是最優選擇。

2.1 k／n（t）：（G）系統根據系統期望的運行時間一次性選擇n

一般而言，k／n（t）：（G）系統要求工作的最小部件數k是一定的，系統容量n（t）視情而定。系統可靠性隨著時間的增加呈現遞減的趨勢。而實際上，當對系統要求較高時，不僅需要表決系統存在k 個或者k 個以上部件工作而且需要系統可靠性R（t）大于事先給定的閾值Pt。系統可靠性與時間以及閾值的關系如下

系統可靠性R（t）分別是關于時間的遞減函數和系統容量的遞增函數，式 （2）給出系統可靠性與系統容量隨時間的關系。根據式 （2）逐一對不同容量系統可靠性的計算，可以確定在系統期望運行時間的要求下k／n（t）：（G）系統的最小容量n（t）。

2.2 k／n（t）：（G）系統以逐步增加部件的方式選擇容量n

基于上述研究，考慮以逐步增加部件的方式運行k／n（t）：（G）系統，即先給定一個小容量n0（n0＞k）的k／n0：（G）系統，使系統開始運行，當系統可靠性下降到閾值Pt時，立即對系統增加一個新部件，系統可靠性升高，當系統可靠性再次下降到閾值Pt時，繼續對系統增加一個新部件，……以此類推，根據上述過程的系統可靠性計算，可以確定在系統期望運行時間內，系統需要的最小容量以及逐步增加部件的時間序列。具體各階段系統可靠性計算公式如下，給定容量n0的k／n0：（G）系統與時間相關的可靠性

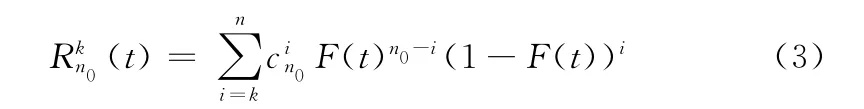
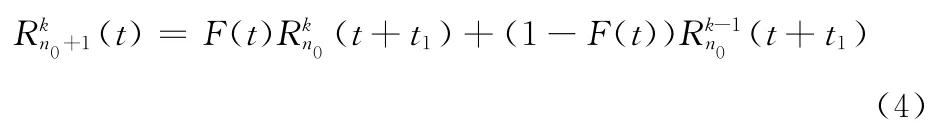
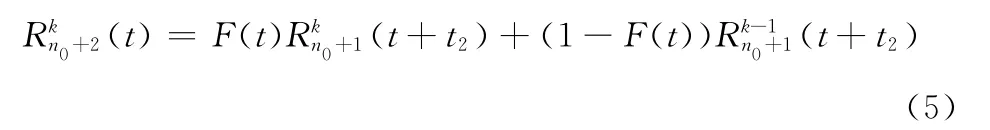
依次類推，可以推導任意容量的系統的可靠性

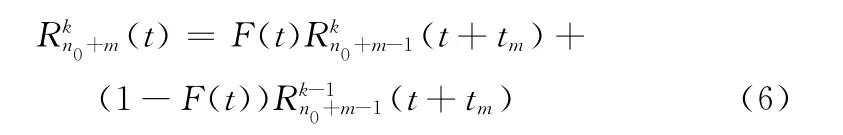
式中：m——某正整數。通過迭代的算法，可以通過已知的信息，計算任意系統容量的可靠性如圖2所示，其中箭頭表示信息的傳遞方向。

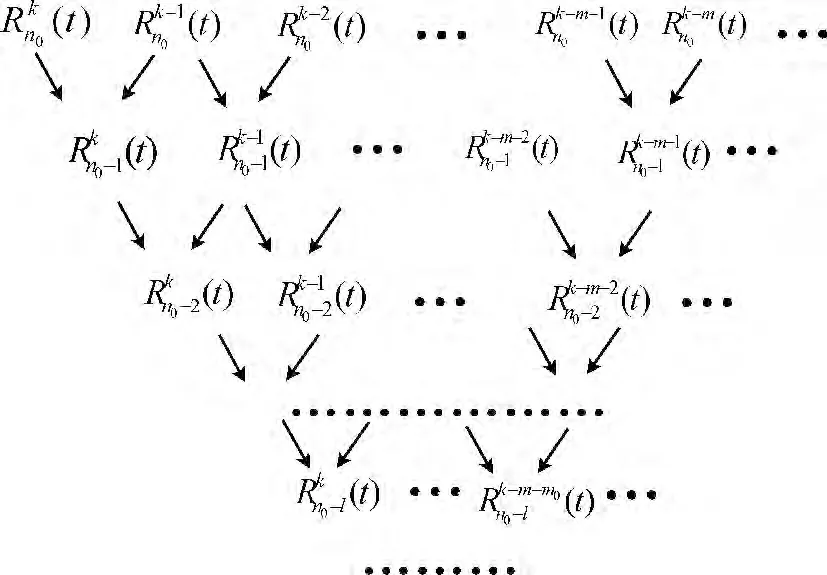
圖2 系統可靠性計算

3 算例研究

針對上述根據系統期望的運行時間一次性選定系統容量以及新提出方法的情況，有必要用數值算例驗證兩種情況優劣。

3.1 k／n（t）：（G）系統根據系統期望的運行時間一次性選擇容量算例研究

設計者常常對系統關鍵部件或者其它部件配置冗余以保證系統可靠性。由于k／n（t）：（G）系統部件屬熱備冗余，能較好的保證系統可靠性，因此被生產部門常采用。對于選擇何種容量的k／n（t）： （G）系統將成為一個優化決策的問題。

同樣認為系統工作所需要的最小部件數k 是一定的，假定k＝50，且要求系統可靠性大于可靠性閾值pt＝0.75時系統才算工作。所有備選部件屬同質部件且壽命Xo（以年記）同分布于W（1.2，0.01；t）。因此不同系統容量n的與時間相關的系統可靠性如圖3所示。

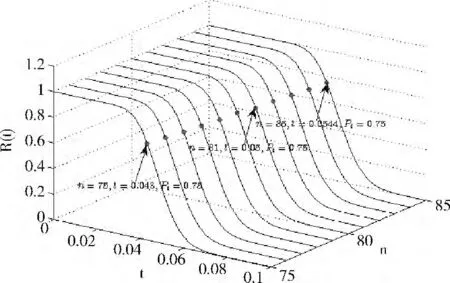
圖3 不同系統容量k／n：（G）系統的可靠性趨勢

其中黑色點為系統在當前容量以及當前閾值下，系統工作與失效的時間分界點。在時間分界點以前系統工作，在分界點后系統失效，即在相應容量下，系統壽命為黑色點對應的時間。因此通過對系統期望的工作時間，可確定最佳的系統容量。不同容量系統可靠性隨時間變化的平面趨勢如圖4所示。

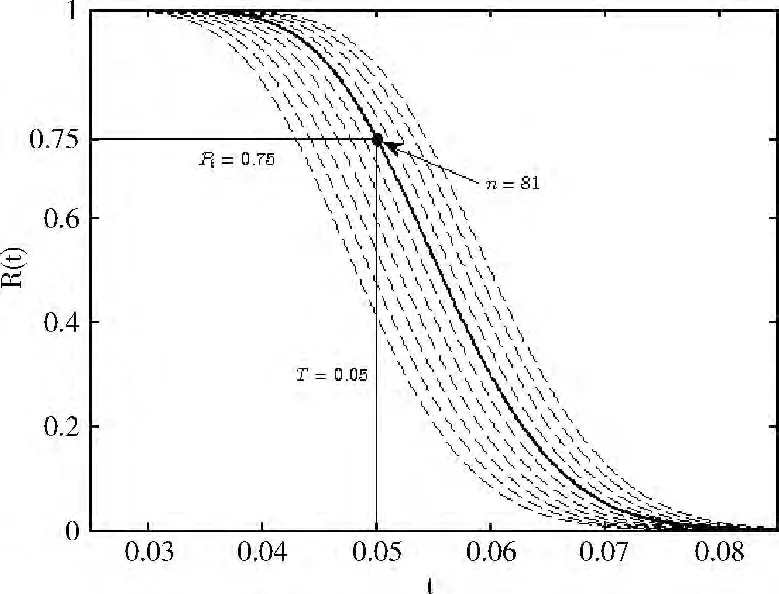
圖4 不同容量系統可靠性隨時間變化的平面趨勢

其中黑色點表示在系統期望的運行時間T＝0.05 年，系統可靠性閾值pt＝0.75時，系統運行需要的最小容量為81。容量低于81的可靠性曲線，系統達不到期望的工作時間而失效，高于81的可靠性曲線，系統工作且可以繼續工作，存在資源的剩余。因此對系統所期望工作的時間不同，系統容量的選擇也不同，表1列舉了對系統不同的期望工作時間下，系統最佳容量的選擇情況。

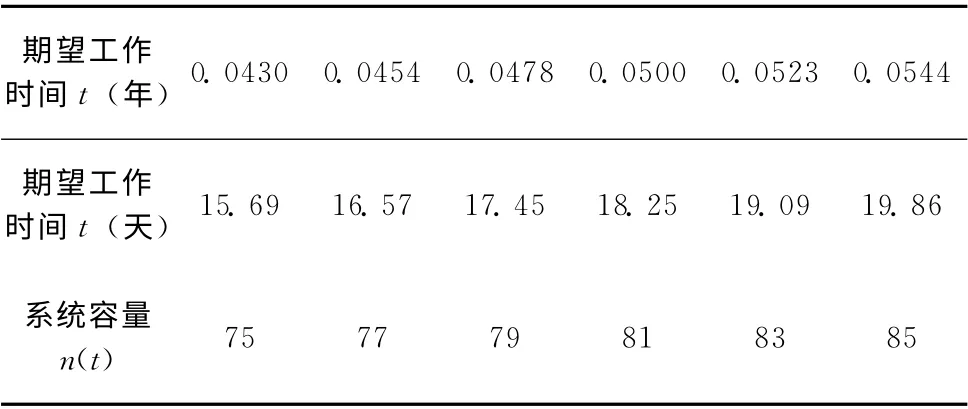
表1 與時間相關的系統容量n（t）

3.2 k／n（t）：（G）系統以逐步增加部件的方式的容量選擇算例研究

事實上，上述系統容量n（t）的選擇并不一定是最優的，因此考慮對k／n（t）：（G）系統逐步增加部件，使系統冗余部件既存在熱備冗余也存在冷備冗余，以此利用冷備冗余在備用過程中不消耗壽命的優勢，節約系統投入使用的部件數量。

以3.1背景為例，選擇初始容量n0＝60 （視情而定）使系統開始運行，當系統可靠性下降到閾值pt＝0.75時對系統增加一個新部件，以此類推，該過程下系統可靠性與時間的關系如圖5實線所示。

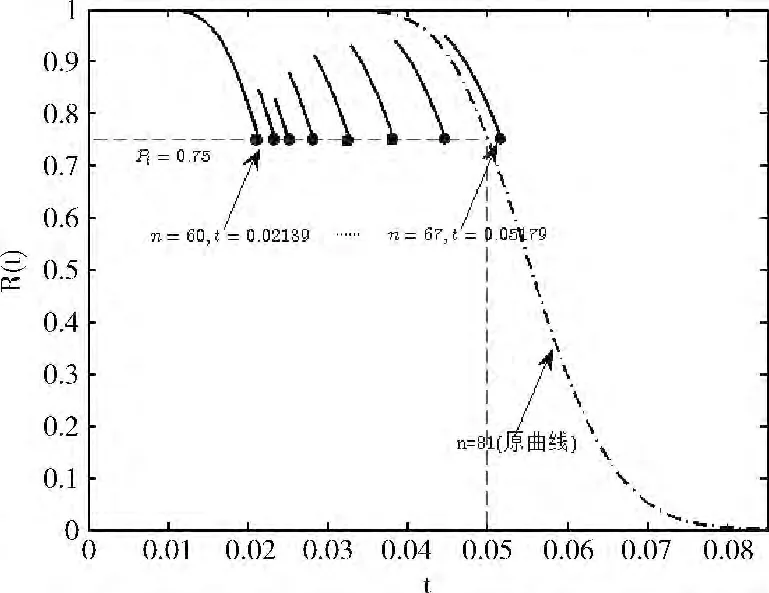
圖5 逐步增加部件的系統可靠性與時間關系

圖5虛線表示原始系統在期望運行時間T ＝0.05 年下，系統最佳容量為81的可靠性曲線圖。而實線表示系統逐漸增加部件的時間以及系統可靠性變化曲線，可以看出在同樣期望工作時間下該系統只需使用67個部件，對比發現，逐步增加部件的方法能夠明顯的減少系統部件的投入使用量。且系統逐步增加部件的時間序列 （以年記）為（0.02139 0.02341 0.02507 0.02825 0.03276 0.03835 0.04477 0.05179），以天記的時間序列為（7.8073 8.5447 9.1506 10.3112 11.9574 13.9976 16.3411 18.9034），因此在期望系統工作的時間T ＝0.05年，即15天的情況下，平均每1～2天增加一個新部件并不算頻繁。表2列舉了該情形下系統最佳容量隨系統不同的期望運行時間的選擇情況。

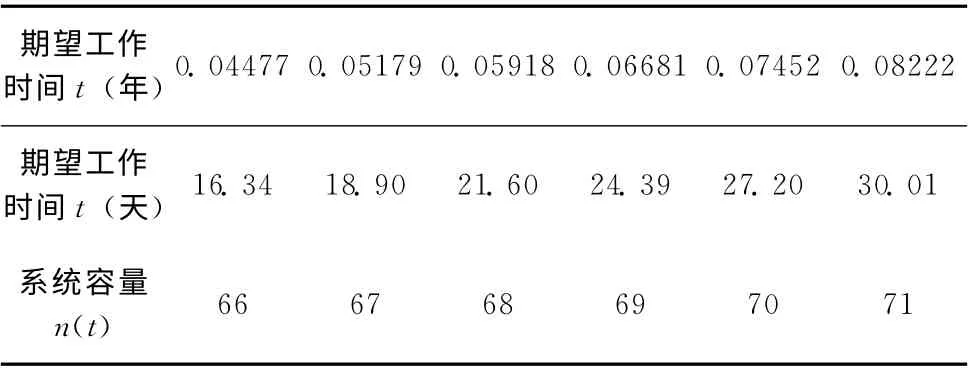
表2 與時間相關的系統容量n（t）

對比表1，表2系統最佳容量的選擇，同樣保證系統工作的條件下，以逐步增加部件的方式的表決系統可以明顯減少系統部件的使用量。兩種情況下系統不同期望時間以及對應的系統容量選擇情況如圖6所示。

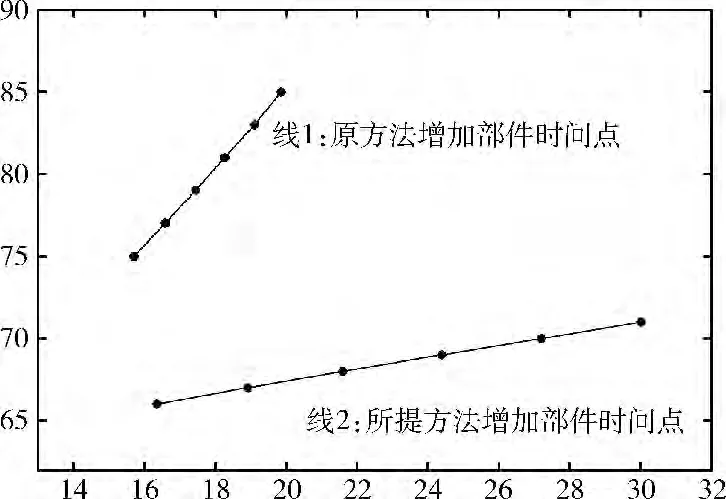
圖6 兩種情況系統最佳容量選擇對比

圖6中線1、線2分別表示原始方法和提出方法兩種情況下系統期望的運行時間與系統需要的最小容量的關系。可以看到線2在同樣系統期望運行的時間下，系統需要的容量明顯小于線1，即提出方法相對原方法有絕對的優勢。

4 提出方法的優越性

首先，從理論上，提出方法 （k／n（t）： （G）系統逐步增加部件的方法）由于消耗性部件并沒有全部一開始就投入使用，因此節約了大量消耗型部件的壽命，在勞動力資本相對部件使用資本足夠小的情況下，提出方法理論上優于原方法。其次，從上述算例模擬研究的結果可以看出新方法具有明顯的優勢。雖然在算法上復雜于原方法，但是通過設計的可靠性計算流程，可以解決算法上的難題，且算法耗時可以很短，因此在實踐上提出方法也優于原方法。對k／n（t）：（G）系統，調整系統使用的最小部件參數k 或者調整部件的參數，均可以通過調整代碼而算出結果，并且得出的結論是一致的。

5 結束語

本文研究最少部件工作數k固定情況下，k／n：（G）系統的最佳系統容量n（t）隨時間的選擇。在系統期望工作時間內，列舉了部分一次性選定的表決系統的最佳系統容量n（t）以及逐步對表決系統增加部件所選擇的最佳系統容量n（t）。并在相同的系統工作時間內，對比了兩種方式所選擇的系統容量，結果顯示在長時間工作的情況下，逐步對表決系統增加部件的方式可以減小部件的使用量，且逐步安裝部件的時間間隔較長，并沒有頻繁的增加部件導致勞動量較大，但不可排除逐步增加單個部件的方式會存在個別時間間隔較短，同時增加兩個或者更多可能更優，但這種情況下，增加不同個數部件會導致系統可靠性計算的困難，因此后續的研究中將考慮個別增加兩個及以上的情況，并進一步考慮該情況系統可靠性的計算的方法。

［1］CAO Jinhua，CHENG Kan.Reliability mathematical introduction ［M］.Beijing：Higher Education Press，2012 （in Chinese）.［曹晉華，程侃.可靠性數學引論 ［M］.北京：高等教育出版社，2012.］

［2］BAO Lei，LI Qingmin，YANG Pinglv.An inventory control model of redundant spare parts for surface ships［J］.Journal of Naval University of Engineering，2012，24 （5）：32－34 （in Chinese）.［包磊，李慶民，楊平律.帶冗余度的航艦隨行備件庫存優化模型［J］.海軍工程大學學報，2012，24 （5）：32－34.］

［3］DU Baojun.The redundant components allocation of continuous k－out－of－n system ［J］.Journal of Lanzhou Jiaotong University，2012，31 （6）：147－153 （in Chinese）. ［杜寶軍.連續n中取k系統中冗余元件的分配問題 ［J］.蘭州交通大學學報，2012，31 （6）：147－153.］

［4］XUE Tao，FENG Yunwen，QIN Qiang.The repairable spare components optimization of K／N cold standby redundant system considering scrapped ［J］.Journal of South China University of Technology，2014，42 （1）：41－46 （in Chinese）. ［薛陶，馮蘊雯，秦強.考慮報廢的K／N 冷備份冗余系統可修復備件優化 ［J］.華南理工大學學報，2014，42 （1）：41－46.］

［5］Tipwimol Sooktip，Naruemon Wattanapongsakom，David W Coit，et al.Multi－objective optimization for k－out－of－n redundancy allocation problem ［C］／／International Conference on Quality，Reliability，Risk，Maintenance，and Safety Engineering，2012：1050－1054.

［6］WANG Zheng，XIE Liyang.Dynamic reliability model of kout－of－n system with dependent failur［J］.Chinese Journal of Mechanical Engineering，2008，44 （6）：72－78 （in Chinese）.［王正，謝里陽.考慮失效相關的k／n 系統動態可靠性模型［J］.機械工程學報，2008，44 （6）：72－78.］

［7］WANG Yongnian.Reliability evaluation of k／n［G］system［J］.Electronics Quality，2009 （10）：37－44 （in Chinese）.［王永年.n中取k 表決系統的可靠性評估 ［J］.電子質量，2009 （10）：37－44.］

［8］CHEN Yanqiao，JIN Jiashan.A simulation algorithm for reliability index of repairable K／N （G）system ［J］.Computer simulation，2008，25 （11）：115－118 （in Chinese）. ［陳硯橋，金家善.可修K／N （G）系統可靠性指標的仿真算法研究［J］.計算機仿真，2008，25 （11）：115－118.］

［9］ZHANG Dingzhou，BAO Lei，QIAN Cunhua.Reliability and maintenance policy of hierarchical voting system subjected to common cause failure［C］／／Reliability Operation Research Society of China Branch of the 8th Conference on Reliability，2009：170－178 （in Chinese）.［張鼎周，包雷，錢存華.基于共因失效的層次表決系統可靠性分析與維護策略［C］／／中國運籌學會可靠性分會第八屆可靠性學術會議，2009：170－178.］

［10］ZHANG Tao，ZHANG Jianjun，GUO Bo.The analysis of（m，N＿G）maintenance strategy of the K／N system based on operational availability ［J］.Journal of Astronautics，2009，30 （1）：395－401 （in Chinese）. ［張濤，張建軍，郭波.基于使用可用度的k／N 系統 （m，N＿G）維修策略分析 ［J］.宇航學報，2009，30 （1）：395－401.］