基于S V M的幼兒成長測評應用
陳卓賀敬
(青島科技大學信息科學技術學院,山東 青島266061)
中國的幼兒教育服務著全世界最龐大的學齡前兒童,由于地域,文化,經濟等差異,教師數量,質量,資源配置,公辦,私營不同,城鄉差距等,幼兒發展的情況幾乎天差地別。幼兒教育對個人乃至社會發展有著重要的、基礎性的、不可或缺的重大意義。如何對幼兒的成長和教育情況予以科學的測評就顯得極具意義。隨著計算機技術和軟件技術的發展,通過建立數據模型,運用一定的算法來分析幼兒成長的各項數據,做出科學合理的測試結果成為可能。
1 支持向量機(Support Vector Machine,SVM)技術
支持向量機方法是建立在統計學習理論的VC維理論和結構風險最小原理基礎上的,根據有限的樣本信息在模型的復雜性(即對特定訓練樣本的學習精度)和學習能力(即無錯誤地識別任意樣本的能力)之間尋求最佳折衷,以期獲得最好的推廣能力的一種機器學習方法[1]。
支持向量機方法是從線性可分情況下的最優分類提出的。即系統產生一個超平面并移動它,使得不同類別的樣本點正好處在該超平面的兩側,這樣得到的平面為最優超平面,從理論上實現了線性可分數據的最優分類問題[2]。如下圖1所示:即L為把x型和o形沒有錯誤地分開的分類線,分別為過各類樣本中離分類線最近點、且平行于分類線的直線,和之間的距離做兩類的分類間隔。所謂最優分類線就是要求分類線不但能將兩類無錯誤地分開,而且要使兩類的分類間隔最大[3]。前者是保證經驗風險最小,使分類空隙最大,實際上就是使推廣性的界中的置信范圍最小,從而使真實風險最小。推廣到高維空間,最優分類線就成為最優分類平面。對于線性不可分情況,通過指定常數C,控制對樣本懲罰的程度,實現在錯分樣本的比例與算法復雜度之間的折衷。
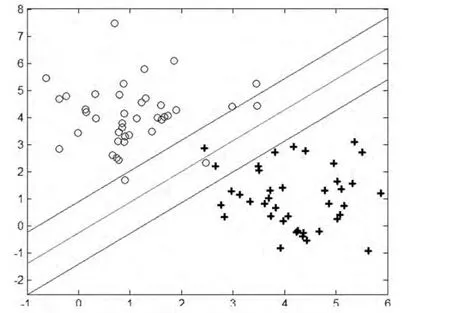
圖1 最優分類示意圖
SVM支持向量機是一項成熟的機器學習方法,在JAVA中我們可以直接調用相應的類。我們需要先建立幼兒測試用的矩陣數據結構,然后據此建立樣本數據。
1)建立應用于幼兒成長測評系統的矩陣,樣本標簽,樣本數據。樣本數據將作為訓練集在程序中使用。
(1)樣本標簽,我們大致將幼兒測試結果分為A出色,B良好,C預警,D干預四類,作為樣本標簽使用,A出色:4分,B良好:3分,C預警:2分,D 干預,1分。
(2)樣本數據,成長測試指標分類見下表(性別男表示為1,女表示為 2):
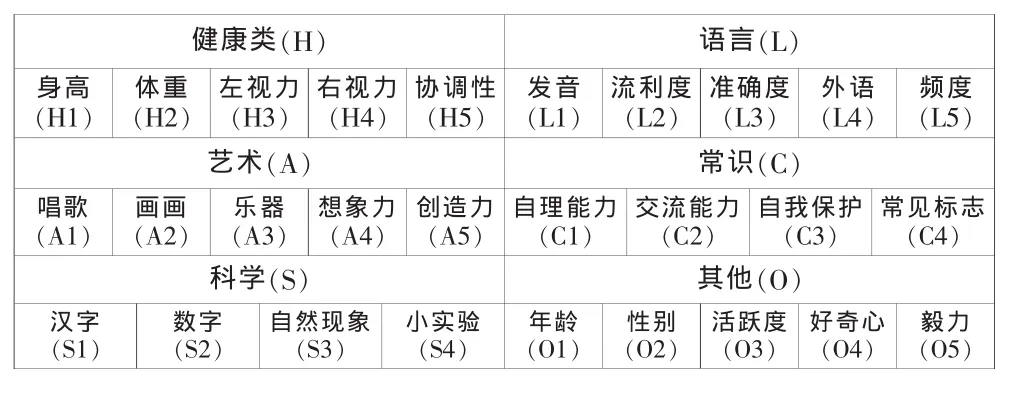
表1 樣本指標
2)通過對學齡前幼兒進行大批量的測試建立樣本數據。樣本該數據越準確,樣本數量越多,得到的效果也就越準確。我們建立樣本數據如下表2。
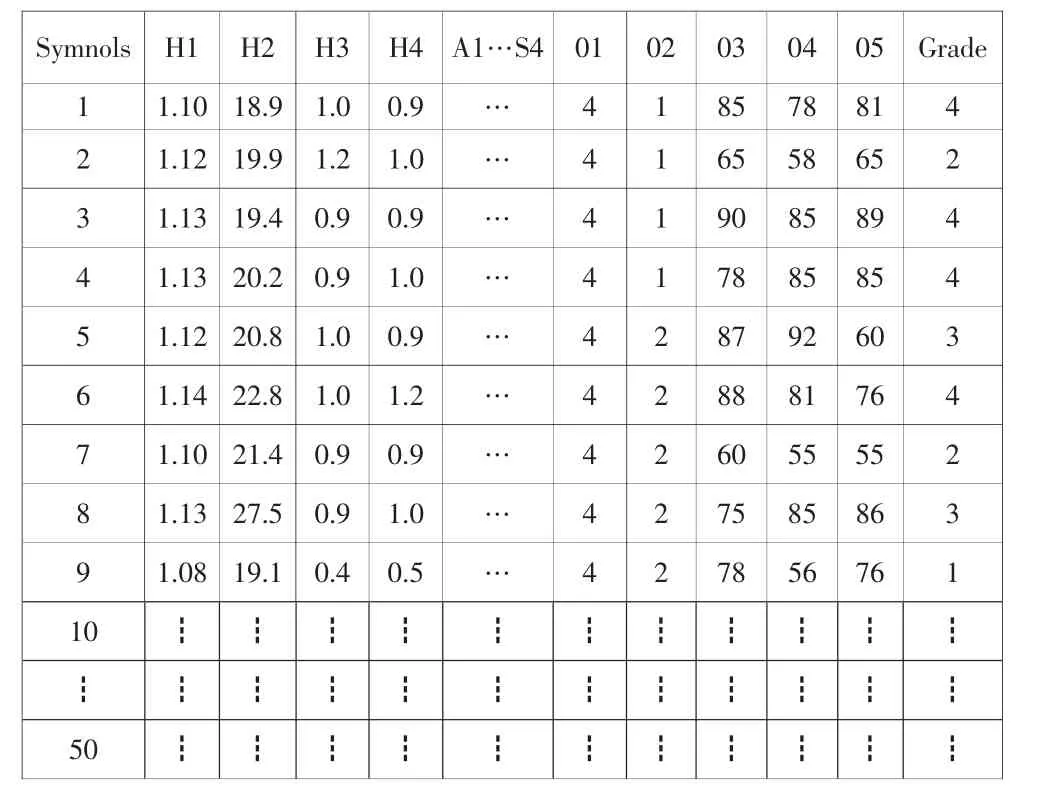
表2 樣本數據
3)分類模型及參數。被評價數據是由4個等級的數據構成,因此該分類屬于多分類問題,考慮到分類的樣式不多,本文選用一對一策略,構造六個支持向量分類器,每個分類器只對兩類進行分類,模型簡單且具有較好的分類能力。
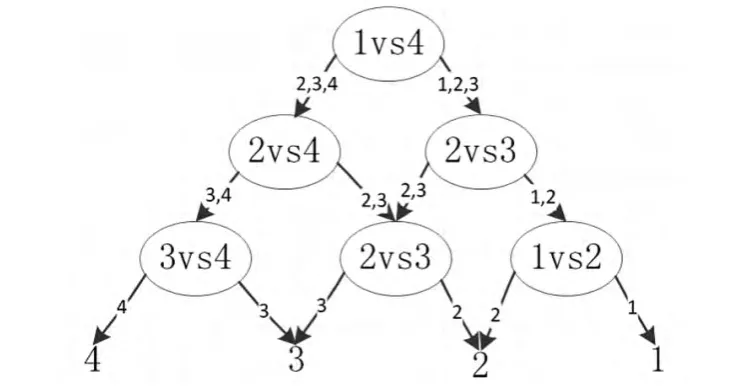
圖2 分類模型示意圖
SVM的核函數采用性能比較好的徑向基核函數:
k(||x-xc||)=exp{-||x-xc||^2/(2*σ^2)
其中xc為核函數中心,σ為函數的寬度參數,控制了函數的徑向作用圍。
2 測試程序及結果
SVM技術在小樣本,非線性,高維度下模式識別方面有著獨有的優勢,在科研和商業上都有著廣泛的應用,很多流行編程軟件都開發了相應的工具包。借助這些工具包我們可以直接調用相應的函數,而不必關心它們是如何實現的。
隨機取5組數據作測試樣本,得到測試結果見下表
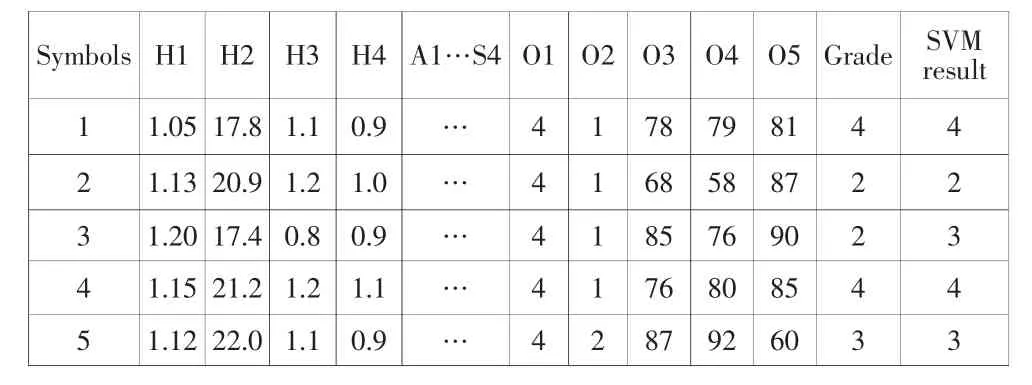
表3 測試結果
從表3可以看出,程序測試結果可以保持不錯的一致性,當然由于這里我們訓練樣本有限,誤差率還比較高。但是隨著訓練樣本的數量增加,優化后的SVM模型準確性會進一步提高,具有廣泛的應用前景。
我們通過對幼兒成長中的各項評價指標進行量化,建立一種基于SVM的模型,應用在實際系統中,取得了比較好的效果,省去了人工評價過程中的不客觀因素,節省了人力成本,擴展了SVM的應用范圍。
[1]何婕.SVM及其在車牌字符識別中的運用[D].四川大學,2005.
[2]王靜.基于GA-SVM的高職學生綜合素質評價模型[J].廣西教育,2014,11:55-57.
[3]朱海林.基于SVM多分類的教學質量評價研究[D].山東師范大學,2009.

