基于三次Bezier曲線逼近的邊緣亞像素定位方法

劉成志++李軍成++楊煉

摘要：圖像邊緣定位是圖像處理研究的一大熱點問題，近年來，國內外學者主要集中于對邊緣亞像素定位方法的研究。本文研究了基于三次Bezier曲線逼近的圖像邊緣亞像素定位方法。首先利用傳統邊緣檢測算子對邊緣點位置進行粗定位，獲得邊緣點的大致位置；然后以邊緣點為中心取若干點作為考察點，利用三次Bezier曲線去逼近所假設的邊緣函數以獲取圖像邊緣的亞像素定位。該方法通過粗、精兩次定位能較快獲得邊緣的亞像素位置，具有定位精度較高，計算速度快等優點。

關鍵詞：三次B ezier曲線；Sobel算子；亞像素定位；精定位

中圖分類號：TP391.4

文獻標識碼：A

DOI： 10.3969/j.issn.1003-6970.2015.07.007

0 引言

在圖像邊緣定位中，常用的方法都是以像素為單位利用一階或二階微分算子進行處理，如Rebort算子、Sobel算子、Prewitt算子、LOG算子和Canny算子等。然而，隨著工業生產的精度越來越高，像素級的邊緣定位已無法滿足實際的需要，許多學者開始致力于邊緣亞像素定位方法的研究。目前，常用的邊緣亞像素定位方法可分為三類：矩法、插值法和擬合（逼近）法。矩法是根據圖像的空間矩、灰度矩、質心及局部能量等保持不變的特性，通過像素灰度值和邊緣的灰度分布計算不同統計量來實現邊緣的亞像素定位。利用矩法進行邊緣亞像素定位時定位精度較高，但其主要采用模板卷積方式，導致其計算速度較慢。插值法是根據圖像邊緣附近像素點的灰度值或灰度值的導數進行插值，通過增加信息量來實現亞像素邊緣檢測。利用插值法進行亞像素邊緣檢測時計算速度較快，但其定位依賴于相鄰像素間的灰度值及坐標，定位精度不高。擬合（逼近）法可具體分為兩種類型：一種是根據假設的邊緣函數，利用圖像邊緣灰度值擬合（逼近）邊緣函數實現邊緣的亞像素定位，主要有多項式擬合法、B樣條擬合法、非線性擬合法等；另一種則是根據假設的邊緣灰度值變化函數，利用圖像邊緣灰度差分值擬合（逼近）邊緣變化函數來實現邊緣的亞像素定位，主要有二次多項式擬合法、高斯曲線擬合法等。利用擬合法進行亞像素邊緣檢測時，其定位精度較高，計算速度比矩法快。

由于擬合法在速度和精度間達到了一定的平衡，通過粗、精兩次定位可較快獲得邊緣的亞像素位置，因此是一種較為合適的邊緣亞像素定位方法。然而，目前利用擬合（逼近）法進行邊緣亞像素定位時，大多采用代數曲線作為擬合（逼近）工具，而鮮有采用參數曲線作為擬合（逼近）工具的研究。為此，本文主要研究了一種基于三次Bezier曲線逼近的邊緣亞像素定位方法。

1 基于三次Bezier曲線逼近的邊緣亞像素定位

1.1 邊緣亞像素定位的基本原理

利用三次Bezier曲線逼近進行亞像素邊緣檢測的步驟是：首先利用傳統邊緣檢測算子對邊緣點位置進行粗定位，獲得邊緣點的大致位置；然后以邊緣點為中心沿邊緣點方向取若干點（一般為3～4個）作為考察點；最后利用三次Bezier曲線去逼近所假設的邊緣函數或邊緣變化函數，通過對三次Bezier逼近曲線求導獲取邊緣的精定位，從而實現圖像邊緣的亞像素定位。利用三次Bezier逼近進行亞像素邊緣檢測的基本過程如圖1所示。

1.2 邊緣的粗定位與取點

所謂邊緣的粗定位，是指利用傳統邊緣檢測方法確定邊緣點的大致位置。傳統的邊緣檢測有Rebort算子、Sobel算子、Prewitt算子、LOG算子和Canny算子等，在利用傳統檢測算子對邊緣進行粗定位時，其優缺點對比如表1所示。

由表1可知，利用傳統檢測算子進行邊緣粗定位時，在速度、精度及噪聲抑制方面不能同時得到滿足。雖然Sobel算子對邊緣的粗定位精度不夠高，由于在空間上容易實現，邊緣檢測效果較好且對噪聲具有一定的平滑作用，因此本文將Sobel算子選作邊緣的粗定位算子。

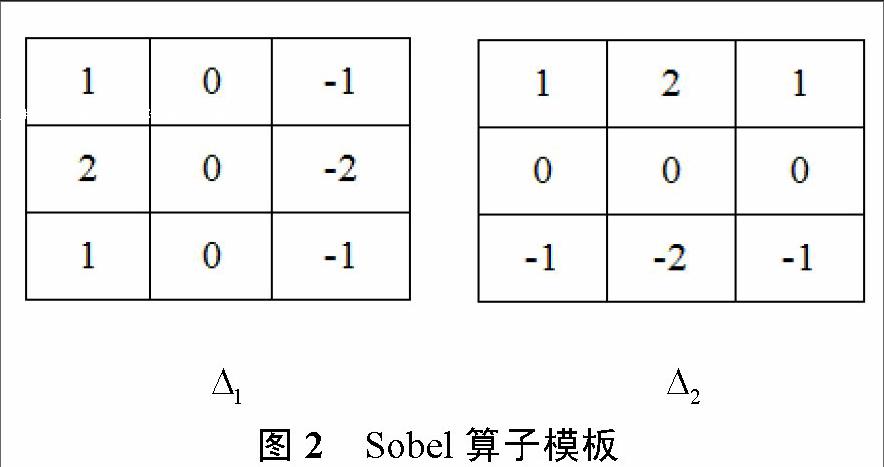
對于數字圖像f（x，y），傳統Sobel算子從水平和垂直兩個方向，利用像素點上下、左右鄰點的灰度加權算法，根據在邊緣點達到極值實現邊緣檢測，其模板如圖2所示。

適當選取某一閾值TH，當S（i，j）>TH時，將（i，j）視為邊緣點，同時也可判斷出邊緣方向。利用Sobel算子獲得粗定位邊緣像素點后，以邊緣點為中心，沿邊緣方向的兩側各拓展2個像素點，得到長度為5的邊緣灰度值向量。

1.3 基于三次Bezier曲線逼近的邊緣精定位

利用Sobel算子對一幅數字圖像的邊緣進行粗定位處理后，得到粗定位邊緣像素點所對應的灰度值向量組{G₁，G₂，…，G_n}，對邊緣灰度值向量G_i（i=1，2，…n）作三次Bezier曲線逼近，可通過求逼近多項式的二階導來獲得精定位邊緣點。

作為一種優秀的曲線造型工具，Bezier曲線已在諸多領域獲得了廣泛的應用。一般地，函數形式的n次Bezier曲線可表示為

其中 為給定的值。

給定連續函數 并取 ，則由式（1）定義的函數形式的n次Bezier曲線又稱為n次Bernstein多項式。由Weierstrass逼近定理可知，在區間[0，1]上可用B ernstein多項式逼近連續函數廠（t），且可達到任意精度。但由于隨著逼近精度的提高，Bernstein多項式的次數也相應提高，會存在計算不穩定的問題，因此在實際應用中，要根據實際情況合理選擇Bernstein多項式的次數。由于是通過求逼近多項式的二階導來獲得精定位邊緣點，因此為了計算方便，本文選擇三次B ernstein多項式作為逼近函數。

當n=3時，式（1）對應的三次Bezier曲線可表示為

設某粗定位邊緣像素點的坐標為（x0，Yo），其邊緣方向為垂直方向。以x0為中心，沿垂直方向的兩側各拓展2個像素點，其水平坐標分別記為X-2，X-1與Xl，X2，并將5個邊緣像素點對應的灰度值向量記為G={g₀，g₁，…，g₄}。

將G的分量看作是區間[o，1]上某邊緣函數f（f）在等距節點 上的取值，即滿足 。由于像素點坐標之間滿足 ，于是像素點坐標x與變量t之間滿足

由式（2）不難推導得B₃（0）=P₀，B₃（1）=p₃，于是利用三次Bezier曲線逼近f（t）時，其表達式可改寫為

下面只需確定式（4）中的P₁與p₂即可實現三次Bezier曲線B₃（t）對邊緣函數f（t）的逼近。由最小二乘原理，可令

由求多元函數取極值的必要條件有式（5）改寫成矩陣形式并計算整理得方程組

將式（6）所得結果P1， P2代人式（4）即得三次Bezier曲線逼近曲線為

其中 為粗定位邊緣像素點的坐標。

同理可得沿水平邊緣方向的精定位像素點（亞像素級）坐標為

其中 為粗定位邊緣像素點的坐標。

例如，利用改進Sobel算子對256x256 （8bit）的標準Lena圖進行邊緣粗定位，其中某一邊緣點的粗定位坐標為（101，119），對應的像素灰度值為73，邊緣方向為垂直方向。以該粗定位邊緣點為中心，沿垂直方向兩側各拓展2個像素點，對應的灰度值分別為127，107，57，54，即所得邊緣灰度值向量G={127，107，73，57，54}。由式（6）計算得P₁=107.6863，P2= 35.3529，將其代人式（8）可得t^*=0.3607，由式（9）可得精定位像素點坐標為（x^*， y^*）= （100.4427，119）。

2 結語

本文提出了一種基于三次Bezier曲線逼近的圖像邊緣亞像素定位方法，通過粗、精兩次定位能較快獲得邊緣的亞像素位置，具有定位精度較高，計算速度快等優點。此外，該方法首次采用參數曲線三次Bezier曲線作為擬合工具來逼近圖像邊緣函數，研究工作具有一定的理論和實際應用價值。在今后的研究工作中，將進一步應用到圖像邊緣亞像素定位的具體實例中。