艦面流場下的直升機(jī)平衡特性分析

徐廣，胡國才，陶楊，王允良

(海軍航空工程學(xué)院飛行器工程系，山東煙臺264001)

0 引言

艦面流場即艦載直升機(jī)的飛行環(huán)境，是直升機(jī)-艦動態(tài)配合的直接影響因素，對直升機(jī)的動力學(xué)建模、平衡特性研究以及飛行仿真都有及其重要的影響。“懸停”跟進(jìn)是直升機(jī)著艦過程中的重要環(huán)節(jié)。在艦面懸停過程中，保持直升機(jī)在艦面流場環(huán)境下的平衡尤為重要。在艦載環(huán)境下，綜合考慮海情、艦船運(yùn)動、甲板上層建筑等因素的影響，艦面流場變得復(fù)雜多變，造成了直升機(jī)安全起降、懸停作業(yè)的困難。不少學(xué)者對不同流場環(huán)境對直升機(jī)飛行特性的影響做了研究，如Labows［1］通過實(shí)驗(yàn)測試了側(cè)風(fēng)經(jīng)過機(jī)庫后形成的流場環(huán)境對黑鷹直升機(jī)懸停平衡操縱量的影響。Horn等［2］通過 CFD(Computational Fluid Dynamics)軟件模擬計(jì)算了城市建筑流場，并結(jié)合飛行員模型研究了該流場對直升機(jī)起降操縱特性的影響。陳仁良［3］重點(diǎn)考慮了直升機(jī)進(jìn)入、沉浸和退出突風(fēng)過程中，突風(fēng)對飛行特性的影響，并計(jì)算了整個過程中直升機(jī)對離散突風(fēng)的響應(yīng)。李軍亮等［4］研究了側(cè)風(fēng)條件下的直升機(jī)懸停配平，并計(jì)算了不同風(fēng)速和風(fēng)向角下的直升機(jī)平衡值。

本文為研究艦面流場環(huán)境對直升機(jī)平衡特性的影響，先采用CFD流體仿真軟件模擬計(jì)算某直升機(jī)母艦甲板上方的流場，再將流場中的風(fēng)速疊加到直升機(jī)旋翼與其他部件中去，形成一個適用于艦面流場計(jì)算仿真的飛行動力學(xué)模型，最后對該模型進(jìn)行配平和響應(yīng)計(jì)算，研究分析艦面流場對直升機(jī)平衡特性的影響。

1 艦面流場仿真

以某型艦船為例，計(jì)算其艦面甲板上方的流場。對艦上建筑與部件的形狀作適當(dāng)簡化，忽略對艦面流場影響較小的建筑與部件。對母艦甲板上方流場的CFD計(jì)算，通過 FLUENT有限體積法求解器完成。

以迎艦艏偏30°方向，大小為15 m/s的定常風(fēng)經(jīng)過艦面高層建筑后在艦面甲板上方形成的流場環(huán)境為例，選取離艦面停機(jī)坪上方約5 m處的區(qū)域作為直升機(jī)懸停跟進(jìn)的位置。

計(jì)算結(jié)果表明，該流場縱向氣流和橫向氣流的分布較為均勻，垂向氣流的變化幅度較大。該位置水平面處的垂向流場分布如圖1所示。經(jīng)大量研究表明，該下沖氣流是海風(fēng)經(jīng)高層建筑后由于陡壁效應(yīng)引起的，是艦面流場環(huán)境下影響直升機(jī)安全起降和平穩(wěn)飛行的重要因素，本文重點(diǎn)研究該氣流對直升機(jī)平衡特性的影響。

圖1 停機(jī)坪流場水平面垂向氣流分布Fig.1 Vertical flow distribution in parking apron

2 直升機(jī)動力學(xué)模型

本文在一個高階非線性飛行動力學(xué)模型［5-6］的基礎(chǔ)上，考慮流場因素的影響，建立一個適用于艦面流場的直升機(jī)動力學(xué)模型。旋翼模型以葉素理論為基礎(chǔ)，采用等圓環(huán)面積法劃分葉素;氣動力模型方面，采用準(zhǔn)定常非線性氣動力模型;在槳葉運(yùn)動方面采用了旋翼槳葉揮舞擺振耦合的剛性槳葉二階動力學(xué)模型;旋翼入流采用動態(tài)入流理論［7］;機(jī)身、平尾和垂尾的氣動載荷采用關(guān)于迎角、側(cè)滑角和馬赫數(shù)的查表函數(shù)的形式求得。尾槳采用簡單的Bailey模型［8］進(jìn)行計(jì)算。

同時(shí)，由于流場的非線性、不均勻性等特點(diǎn)，會對直升機(jī)各部件的氣動載荷分布產(chǎn)生變化。由于槳葉直徑遠(yuǎn)大于流場尺度，槳葉不同分段處的流場風(fēng)速各不相同，其梯度變化也較大，對葉素氣動載荷計(jì)算結(jié)果的影響不可估量，對整體旋翼的氣動載荷造成了影響，因此，本文采用了一種旋翼空間離散模型，從槳葉剖面的相對氣流速度項(xiàng)出發(fā)，將旋翼的前進(jìn)比細(xì)化為每片槳葉不同分段位置處的當(dāng)?shù)厍斑M(jìn)比，在當(dāng)?shù)厍斑M(jìn)比中考慮當(dāng)?shù)氐牧鲌鲲L(fēng)速矢量，從而修改了對槳葉任意葉素剖面氣流速度的計(jì)算公式，計(jì)算得到了流場中的旋翼氣動載荷。流場對機(jī)身、尾翼和尾槳模型的影響可采用簡化的方法，將各自部件重心位置處的流場風(fēng)速矢量疊加到部件的相對速度中即可。

由此得到直升機(jī)的非線性狀態(tài)方程組:

3 平衡特性分析

3.1 配平計(jì)算

本文采用了UH-60A黑鷹直升機(jī)作為樣例直升機(jī)，所有仿真均以直升機(jī)在流場中的配平值作為初始值，因此，首先對其進(jìn)行艦面流場環(huán)境下的配平計(jì)算。為提高配平計(jì)算效率，本文采用了一種嵌入式LM算子的粒子群算法［9］。

以迎艦艏偏右舷30°方向，大小為15 m/s的海風(fēng)經(jīng)過艦面高層建筑后在艦面甲板上方形成的流場環(huán)境為例，采用對應(yīng)的CFD仿真計(jì)算結(jié)果。同時(shí)，為分析艦面流場對直升機(jī)平衡特性的影響，以直升機(jī)在對應(yīng)的陸基常值風(fēng)條件下的計(jì)算結(jié)果作為對比。此外，直升機(jī)動力學(xué)模型的不同也會對結(jié)果產(chǎn)生影響。因此，本文在仿真中選取了旋翼離散模型(以葉素在不同位置處的風(fēng)速作為當(dāng)?shù)貧饬魉俣?和無離散模型(以旋翼中心處的風(fēng)速作為旋翼所有葉素的氣流速度)兩種模型作對比驗(yàn)證。

3.2 流場對旋翼入流的影響

圖2給出了第1片槳葉徑向分段的葉素在不同槳葉方位角位置處的垂向氣流速度Vcx。由圖可知，葉素的垂向氣流速度分布隨著槳葉方位角變化，呈現(xiàn)出不規(guī)則圓頻率曲線的趨勢。內(nèi)段葉素氣流速度更接近槳盤中心，分布也更為均勻，隨著葉素由內(nèi)段到外段，氣流速度的變化幅度和分布的隨機(jī)性也隨之增大。

圖2 葉素垂向風(fēng)速分布圖Fig.2 Blade element vertical velocity distribution

圖3 給出了葉素入流Vrl的變化，以旋翼無離散模型計(jì)算的入流速度作為對比。葉素的入流取決于旋翼入流模型和葉素氣流速度的影響，本文采用了動態(tài)入流模型，兩種模型是一致的。在氣流場方面，無離散模型中所有葉素處的氣流速度均取自旋翼中心處，因此，其入流速度呈現(xiàn)的是標(biāo)準(zhǔn)的圓頻率曲線。而在旋翼離散模型中，由圖2可以看出，葉素氣流的分布存在非線性、不均勻等特性，基于此，該模型中的葉素入流并不規(guī)則，且離旋翼中心越遠(yuǎn)的葉素入流與圓頻率曲線差距越大。

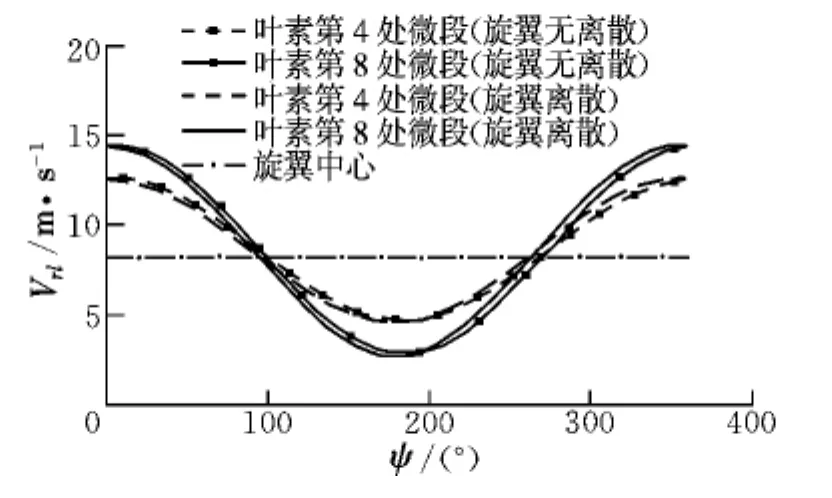
圖3 葉素入流分布Fig.3 Blade-element inflow distribution

3.3 流場對旋翼載荷和功率的影響

圖4 和圖5分別給出了單片槳葉的拉力Fdp和旋翼的拉力Fxy隨槳葉方位角的變化趨勢。由于UH-60A直升機(jī)是4片槳葉對稱分布，平衡狀態(tài)下的旋翼拉力也是對稱分布的，因此，圖5只給出了1/4旋翼旋轉(zhuǎn)周期的旋翼拉力。陸基流場和艦基流場兩種環(huán)境下的槳葉拉力相差較大，這是由于海面自由風(fēng)經(jīng)過艦面甲板上方的高層建筑后，改變了氣流場的結(jié)構(gòu)，從而影響了槳葉和旋翼的氣動力。旋翼離散模型計(jì)算的單片槳葉拉力和旋翼拉力在與無離散模型計(jì)算的對比中，槳葉旋轉(zhuǎn)一周的平均拉力非常接近，其中后者隨槳葉方位角的變化趨勢與定常風(fēng)場環(huán)境下的旋翼拉力較為相似，而前者的變化趨勢略有不同，幅度較前者要劇烈一些，表明旋翼氣動載荷受流場因素的影響較為明顯，尤其是槳盤上垂向氣流的不均勻分布影響了旋翼周向位置上的拉力分布，不能簡單地用旋翼中心處的氣流替代。旋翼離散模型在旋翼垂向載荷計(jì)算方面顯然更能體現(xiàn)艦載環(huán)境的特點(diǎn)，計(jì)算結(jié)果也是更為準(zhǔn)確的。

圖4 單片槳葉拉力Fig.4 Single blade thrust

圖5 旋翼拉力Fig.5 Main rotor thrust

圖6 給出了旋翼功率Pxy隨槳葉方位角的變化趨勢。

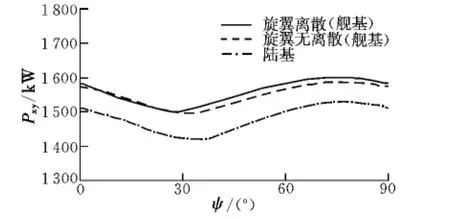
圖6 旋翼功率Fig.6 Main rotor power

由圖可知，相較于旋翼拉力，旋翼功率隨著槳葉方位角的變化較為平緩，而旋翼的功率主要由旋翼扭矩決定，槳葉切向載荷又是扭矩的主要影響因素，這表明槳葉切向氣動載荷受氣流場的影響不大。陸基和艦基環(huán)境在流場方面的差異在上文中已進(jìn)行了詳細(xì)分析。實(shí)際上，由于槳葉處于高速旋轉(zhuǎn)中，葉素在氣流場中的切向氣流速度相較于槳葉轉(zhuǎn)速而言對氣動力的貢獻(xiàn)較小，甚至可忽略不計(jì)。但是由于垂向氣流分布的區(qū)別造成了旋翼整體氣動載荷的區(qū)別，從而導(dǎo)致兩種模型在旋翼扭矩和功率的計(jì)算上存在著細(xì)微差距，但在旋翼切向氣動載荷計(jì)算方面，兩種模型計(jì)算的區(qū)別不大。

3.4 流場對機(jī)體姿態(tài)的影響

直升機(jī)的平衡狀態(tài)一般是指旋翼旋轉(zhuǎn)周期下的平均加速度為零。實(shí)際上，由于旋翼在每個方位角處的載荷不同，導(dǎo)致機(jī)體在每個時(shí)刻下均存在加速度，隨著時(shí)間的延長和誤差的積累，會造成機(jī)體姿態(tài)的變化，影響直升機(jī)的平衡。

圖7給出了機(jī)體姿態(tài)角加速度隨槳葉方位角的變化趨勢，并與旋翼無離散模型的計(jì)算結(jié)果進(jìn)行了對比。由圖可知，平衡狀態(tài)下兩種模型計(jì)算的角加速度數(shù)量級均較小，且周期平均角加速度均接近于零。

圖7 機(jī)體姿態(tài)角加速度Fig.7 Attitude angle acceleration

圖8 給出了直升機(jī)機(jī)體偏航角速率隨時(shí)間的響應(yīng)。

圖8 機(jī)體偏航角速率響應(yīng)Fig.8 Response of yaw rate

由圖8可知，隨著加速度的積累，仍不可避免地破壞了直升機(jī)姿態(tài)的平衡。其中，旋翼離散模型的姿態(tài)角速率變化較快，實(shí)際上，由于機(jī)體加速度的積累，機(jī)體姿態(tài)逐漸偏離平衡狀態(tài)，不同時(shí)刻下同一處葉素在空間流場中位置是不同的，從而導(dǎo)致每一時(shí)刻下的葉素入流也存在差異，影響了模型的氣動載荷。旋翼無離散模型由于將旋翼所處的氣流場視為同一風(fēng)速，尚不明顯，而旋翼離散模型中，艦面流場氣流的不均勻分布加劇了這一影響，導(dǎo)致姿態(tài)角速率在響應(yīng)的后期發(fā)散加快。三個姿態(tài)方向的相互耦合加速破壞了機(jī)體的平衡，進(jìn)一步加劇了機(jī)體姿態(tài)偏離初始平衡狀態(tài)。這就對直升機(jī)在艦面流場環(huán)境下的操縱提出了更高的要求，需要開發(fā)適用于艦載環(huán)境的飛行控制系統(tǒng)維持直升機(jī)在母艦甲板上方懸停過程中的姿態(tài)穩(wěn)定，以配合下一步直升機(jī)著艦的過程。

4 結(jié)論

(1)建立了某型艦船的CFD仿真模型，通過數(shù)值仿真，得到了不同環(huán)境條件下的母艦甲板上方的流場分布。由分析可知，由于機(jī)庫等高層建筑的存在改變了流場的結(jié)構(gòu)，在甲板上方形成了下沖氣流，因此會對直升機(jī)的懸停、起降和空中作業(yè)產(chǎn)生嚴(yán)重的影響。

(2)建立了適用于艦載環(huán)境的直升機(jī)飛行動力學(xué)模型，考慮了旋翼徑向與流場尺度的關(guān)系，對旋翼槳盤進(jìn)行了離散計(jì)算，將流場氣流速度通過旋翼分段的位置疊加到每一處葉素中，修正了葉素的氣動載荷計(jì)算公式。

(3)通過對旋翼入流、載荷和功率的分析，表明艦面流場在直升機(jī)旋翼處的垂向氣流分布是不均勻的，對槳葉和旋翼垂向載荷的影響較為明顯。通過對機(jī)體姿態(tài)響應(yīng)的分析，表明艦面流場環(huán)境對直升機(jī)機(jī)體姿態(tài)的影響是巨大的，其流場特性決定了保持機(jī)體姿態(tài)平衡的困難度，亟待開發(fā)一種適用于艦載環(huán)境的飛行控制系統(tǒng)。

［1］ Labows S J.UH-60 blackhawk disturbance rejection study for hover low speed handling qualities criteria and turbulence modeling［D］.California:Naval Postgraduate School，2000.

［2］ Horn JF，Keller JD，Whitehouse GR，et al.Analysis of urban airwake effects on heliport operations at the chicago children’s memorial hospital［R］.Report for Illinois Department of Transportation，2001.

［3］ 陳仁良.直升機(jī)對離散突風(fēng)的響應(yīng)［D］.南京:南京航空航天大學(xué)，1988.

［4］ 李軍亮，胡國才，王浩.側(cè)風(fēng)對艦載直升機(jī)懸停性能的影響［J］.海軍航空工程學(xué)院學(xué)報(bào)，2010，25(2):129-132.

［5］ Howlett J J.UH-60A black hawk engineering simulation program［R］.NASA-CR-166309，1981.

［6］ Kim F D.Formulation and validation of high-order mathematical models of helicopter flight dynamics［D］.Maryland:University of Maryland，1994.

［7］ Pitt D M，Peters D A.Theoretical prediction of dynamic inflow derivatives［J］.Vertica，1981，5(1):21-34.

［8］ Bailey F J.A simplified theoretical method of determining the characteristics of a lifting rotor in forward flight［R］.NASA-TR-716，1941.

［9］ Xu G，Hu GC，Chen JF.A new PSOalgorithm LM operator embedded in for solving systems of nonlinear equations［C］//Sixth International Conference on Intelligent Human-Machine Systems And Cybernetics.Hangzhou:IEEE Computer Society，2014:142-145.