高速旋轉條件下的彈丸氣動特性研究

馬 杰，陳志華，姜孝海

（南京理工大學 瞬態物理國家重點實驗室，南京210094）

為了讓彈丸獲得很好的穩定性，通常采用帶尾翼或高速旋轉2種方式［1］，其中高速旋轉彈丸利用陀螺穩定性原理，在飛行過程中以錐形運動螺旋前進以保證其飛行穩定性［2－4］。旋轉彈丸及某些火箭彈和導彈在飛行過程中以一定攻角繞自身縱軸旋轉，當攻角不為0，會產生垂直于攻角平面的側向力，稱為馬格努斯力，由此產生的力矩稱為馬格努斯力矩。一般情況下，馬格努斯力約為相應法向力的1%～10%［5］，但因在全彈道上不被阻尼，故對彈丸動穩定性有重要影響，因而研究旋轉彈丸的馬格努斯效應具有非常重要的意義［6］。

世界各國對馬格努斯效應開展了大量研究工作，尤其是在旋轉彈箭的運用方面。近年來，隨著計算流體力學（CFD）的發展，對高速旋轉彈丸的數值模擬也日趨普遍，其中主要包括雷諾平均方法（RANS）與分離渦方法（DES）［6－10］。

本文對制式彈丸的流場進行了數值模擬，分析了旋轉對彈丸升阻力的影響以及馬格努斯效應的產生機理，研究了攻角、馬赫數以及轉速變化時，彈丸表面壓力分布與馬格努斯力和力矩系數隨著上述參數的變化規律，以及提出了一定條件下的馬格努斯系數公式。

1 數值模擬方法

本文基于三維雷諾平均方程，采用realizablek－ε湍流模型，對高速旋轉彈丸的流場進行了數值模擬。為了模擬非定常情況下彈丸的旋轉狀態，本文采用滑移網格技術對其模擬仿真。

本文選取長為六倍口徑的SOCBT彈丸［6］為物理模型。計算域的網格分為外部固定區和內部滑移運動區。圖1為彈體附近的滑移網格示意圖。由圖可知，彈丸表面附面層內網格沿法向進行了加密，而在彈丸的彈頭與彈肩及彈尾等有轉折處網格沿流向都進行了加密，經多次計算并達到網格收斂后，整個區域的網格數取約250萬。

圖1 彈體附近的滑移網格

彈體表面采用無滑移壁面邊界條件，網格隨彈體一起運動；外部固定網格區和內部網格運動區的交界面均采用滑移邊界條件。外部固定區的外邊界采用壓力遠場邊界條件，其中來流條件為：馬赫數Ma＝3，總溫T0＝310K，總壓p0＝2.985×105Pa，彈丸攻角變化范圍α＝0～12°，分別取無量綱轉速Ω＊＝0.19（相當于轉速為20 000r／min）和Ω＊＝0。Ω＊＝ΩD／v∞，Ω為轉速，D為彈丸最大直徑，v∞為來流速度，從彈尾向頭部看去逆時針旋轉。

2 數值模擬結果與分析

圖2為馬赫數Ma＝3，轉速Ω＊＝0，攻角為6°時，彈丸表面壓力pw分布的實驗結果與數值結果對比圖。轉速為Ω＊＝0.19時，彈丸馬格努斯力系數Cz和力矩系數Cmy與相應的實驗數據對比圖如圖3所示。由圖2可知，對于無旋彈丸，數值模擬結果所得到的表面不同位置軸向壓力系數與實驗結果［11］幾乎完全相同。而對于旋轉彈，從圖3中可以看出，在小攻角（≤6°）時，計算值與實驗值吻合得非常好。隨著攻角的變大，因流場的復雜性而使計算結果與實驗值之間的偏差變大，當攻角α＝6°時，兩者相差約為11%，而當α＝12°時，相差則高達25%，此時計算結果與實驗結果不再有可比性。因此，本文以下主要討論攻角α≤6°的情況。

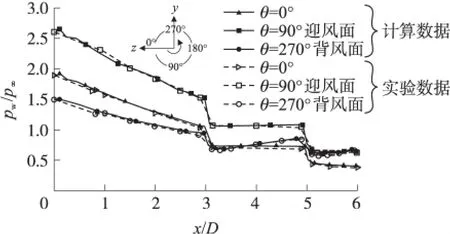
圖2 彈丸表面壓力的實驗數據［6］與計算數據對比圖

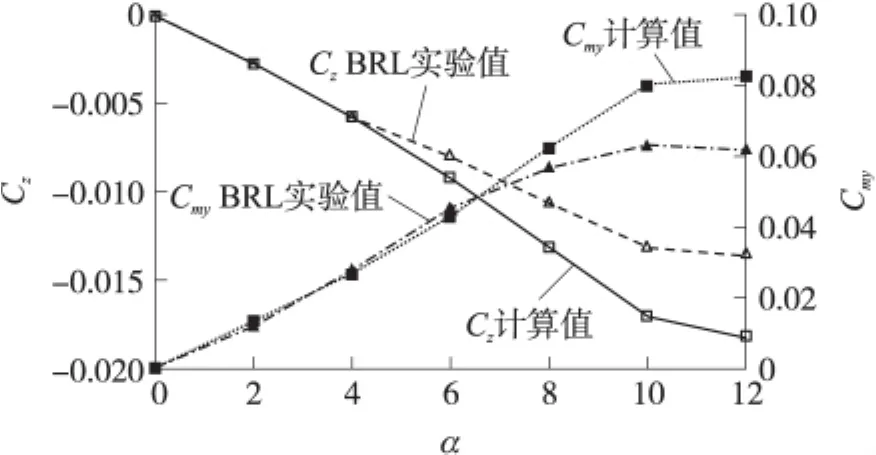
圖3 馬格努斯系數計算值與實驗值對比［11］

圖4 為馬赫數Ma＝3，攻角α＝6°，轉速Ω＊＝0.19時，彈丸表面以及xoy面上半部與xoz面的右半部上的壓力分布云圖。由圖4可知，彈丸頭部存在典型斜激波結構，而頭部與彈體及彈船尾段則存在膨脹波，因而其壓力較頭部小，整個彈丸附近的波系結構與無旋彈的波系結構相似。

馬赫數Ma＝3，攻角為6°，轉速分別為Ω＊＝0和Ω＊＝0.19時，不同位置的橫向截面yoz上的渦量云圖及流線分布如圖5和圖6所示。從圖5可知，對于位置x／D＝4.37和5.77，無旋彈丸的渦量和流線基本對稱，在彈體上部有2個駐定的旋向相反且大小相等的渦對；而對于旋轉彈丸（圖6），此兩位置的渦量與流線分布不再對稱，左邊負向渦對變大，正是由于彈體攻角背面尾渦的不對稱性，導致其對應位置表面壓力的分布不對稱。

圖4 Ma＝3，Ω＊＝0.19且α＝6°時彈丸表面及側向的壓力分布

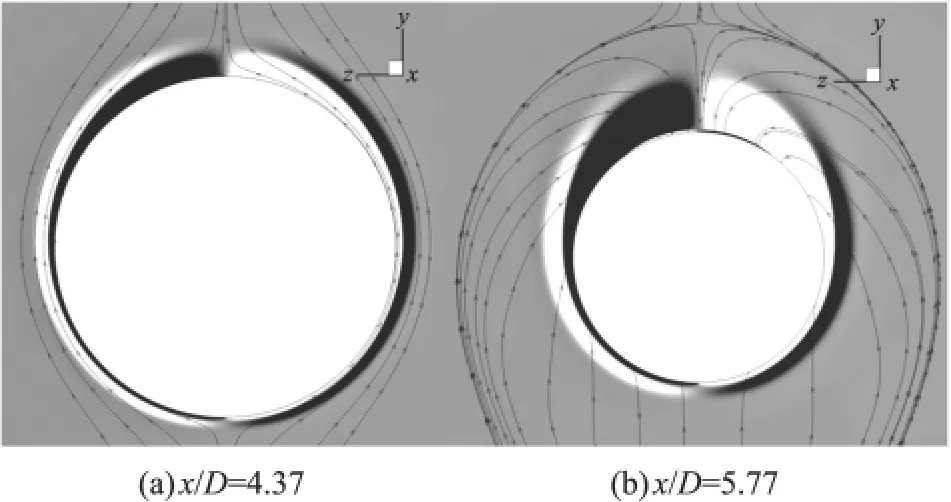
圖5 Ω＊＝0時橫截面x／D＝4.37和5.77的渦量及流線分布

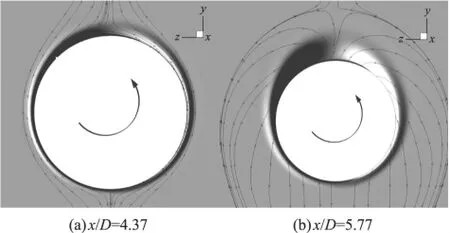
圖6 Ω＊＝0.19時橫截面x／D＝4.37和5.77渦量及流線分布

馬赫數Ma＝3，攻角為6°，轉速分別為Ω＊＝0和Ω＊＝0.19時，橫向截面不同位置上的壓力分布等值線如圖7和圖8所示。從圖8可知，當彈體不旋轉時，橫截面上的壓力分布關于攻角平面對稱。當旋轉時（圖8），彈丸左側橫流與環流方向相反，速度降低，而右側剛好相同，流速加快，導致邊界層發生變化，內部速度分布不再對稱。左側因速度降低，邊界層變厚，壓力開始變大，引起低壓區收縮，而右側邊界層因速度增加，邊界層變薄，使壓力開始降低，右側低壓區擴大，彈體表面流體分離位置發生變化，從而使尾渦不再對稱，導致彈體兩邊壓力分布不再相等。綜上所述，左側低壓區縮小，右側低壓區擴大，從而使左側壓力高于右側，導致產生側向力，即馬格努斯力的產生。

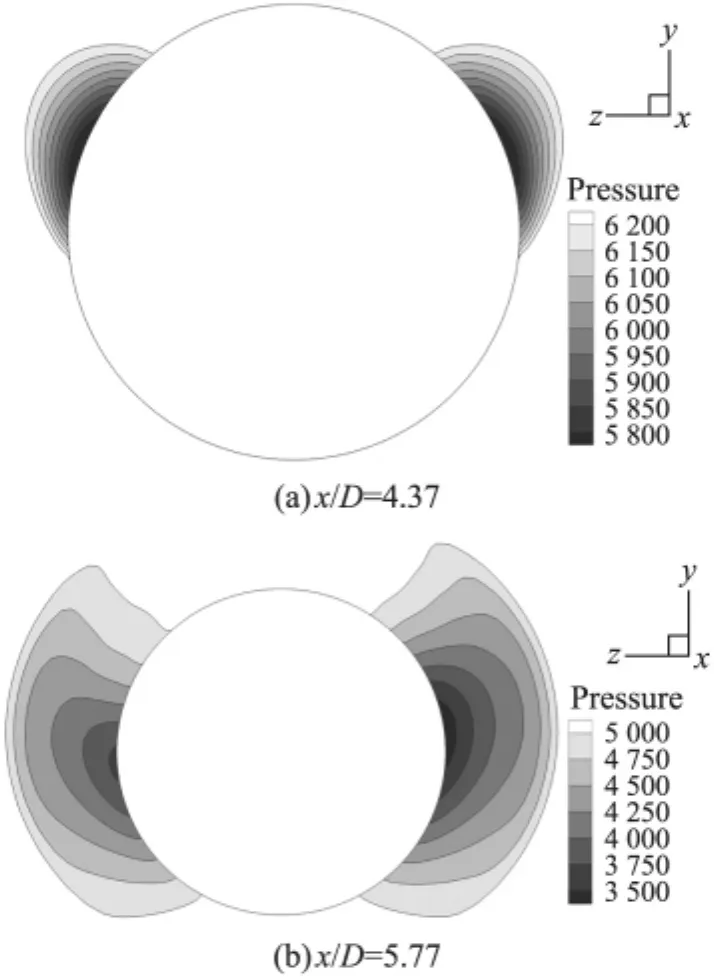
圖7 轉速Ω＊＝0時橫向截面壓力分布圖

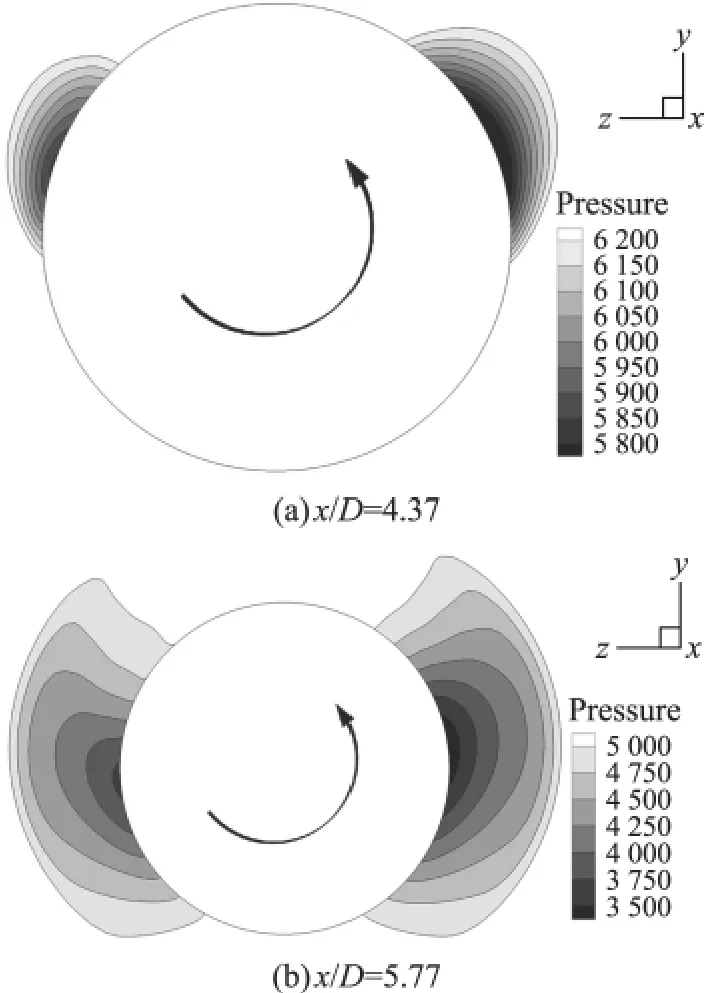
圖8 轉速Ω＊＝0.19時橫截面壓力分布圖

圖9 為馬赫數Ma＝3，攻角為6°時，旋轉和無旋彈丸沿彈體不同截面的周向表面壓力系數（pw／p∞）分布圖。可知，對于圖9（a），旋轉彈丸和無旋彈丸圓柱段迎風面壓力非常接近，而在背風面，旋轉彈丸右側（即180°～270°）壓力值明顯較無旋彈丸小，左側270°～285°左右壓力值較無旋彈也略小，但是在285°～360°范圍壓力值明顯超過了無旋彈丸壓力值，同時知道左右兩側無旋彈的壓力值對稱，這就證明了背風面旋轉彈丸表面左側壓力整體高于右側彈丸表面壓力。同樣觀察圖9（b），在迎風面旋轉彈丸船尾部表面壓力總體較無旋彈丸大，右側幾乎接近不變，略有變小；在背風面與圓柱段相似，同樣產生z軸負方向側向力。船尾壓差較圓柱部分的壓差要大。

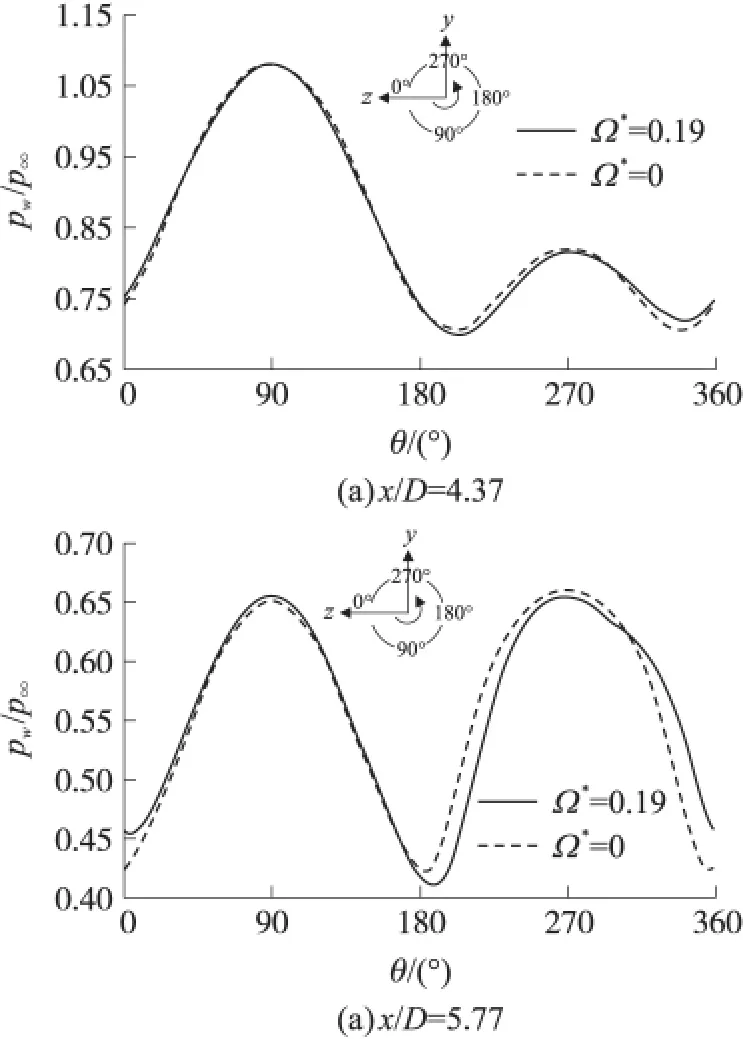
圖9 橫截面處周向彈體表面壓力系數分布圖

2.1 不同轉速條件下彈丸阻力與升力系數變化

無旋彈丸與旋轉彈丸阻力系數及差值如圖10所示。

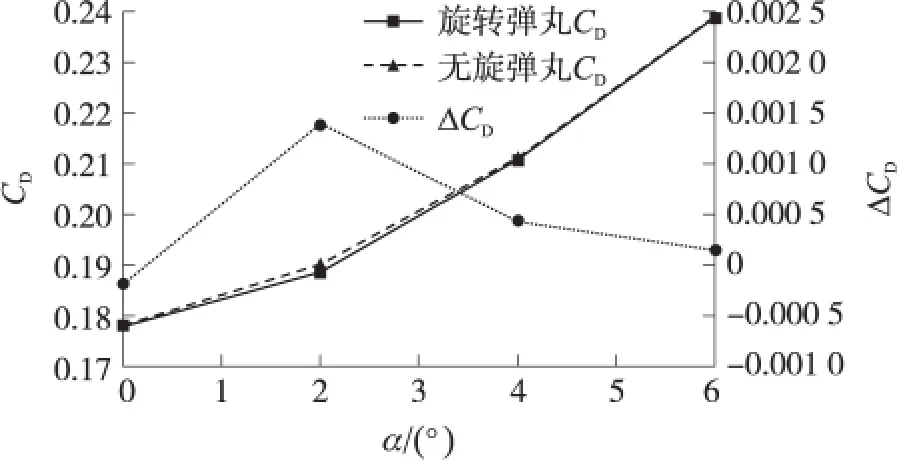
圖10 無旋彈丸與旋轉彈丸的阻力系數及其差值

從圖10中可以看出，無旋彈丸與旋轉彈丸阻力系數差別不大，在小攻角情況下，旋轉彈丸的阻力系數比無旋彈丸的阻力系數要小，可以認為在小攻角情況下，旋轉效應會導致彈丸的阻力系數偏小。從圖11可以看出，無旋彈丸與旋轉彈丸升力系數幾乎重疊，受到馬格努斯效應影響不是很大；旋轉影響導致彈丸的升力要比無旋彈丸的升力大，在0°～4°攻角差值時線性變化，超過4°攻角差值逐漸趨于穩定。

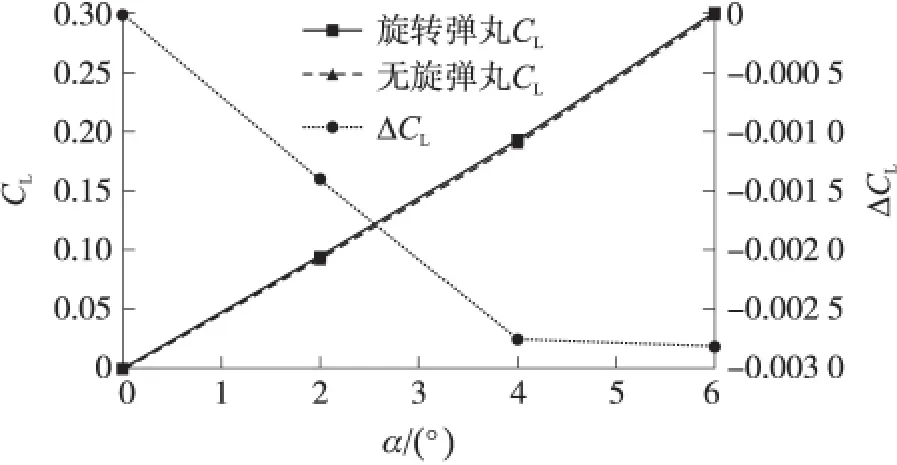
圖11 無旋彈丸與旋轉彈丸的升力系數及其差值

圖12 為不同轉速情況下彈丸的表面壓力分布。

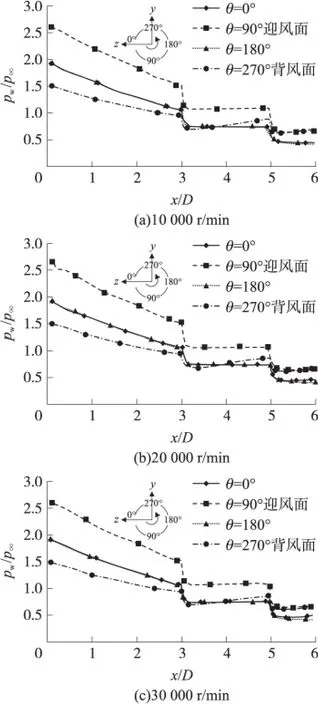
圖12 馬赫數Ma＝3，攻角為6°時彈丸的表面壓力分布

從圖13可以看出，迎風面和背風面壓力幾乎沒有變化，這說明旋轉快慢對升力影響不大，再看彈丸的θ＝0°和θ＝180°兩側，彈頭和圓柱部位壓力分布也幾乎沒有什么變化，同樣影響彈丸氣動力的還是在船尾處。隨著轉速的提升，雖然彈尾部壓力值變化不大，但兩側的壓力值表現為一側變大（θ＝0°），

2.2 旋轉彈丸馬格努斯力與力矩系數隨轉速與攻角的變化

而另一側變小（θ＝180°），因此彈尾部側向壓差明顯增大。這表明，隨著轉速的增大，馬格努斯現象影響越來越大。

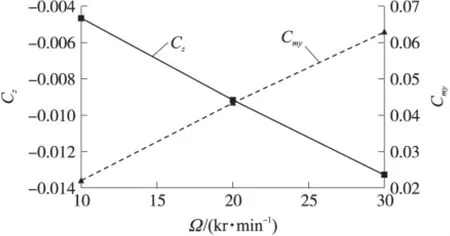
圖13 馬格努斯系數隨轉速的變化情況

從圖13可以看出，在其他條件相同時，馬格努斯力以及力矩不僅隨著轉速的增大而增大，而且是呈線性變化。Ma＝3，Ω＊＝0.19時不同攻角情況下彈丸的表面壓力分布如圖14所示。

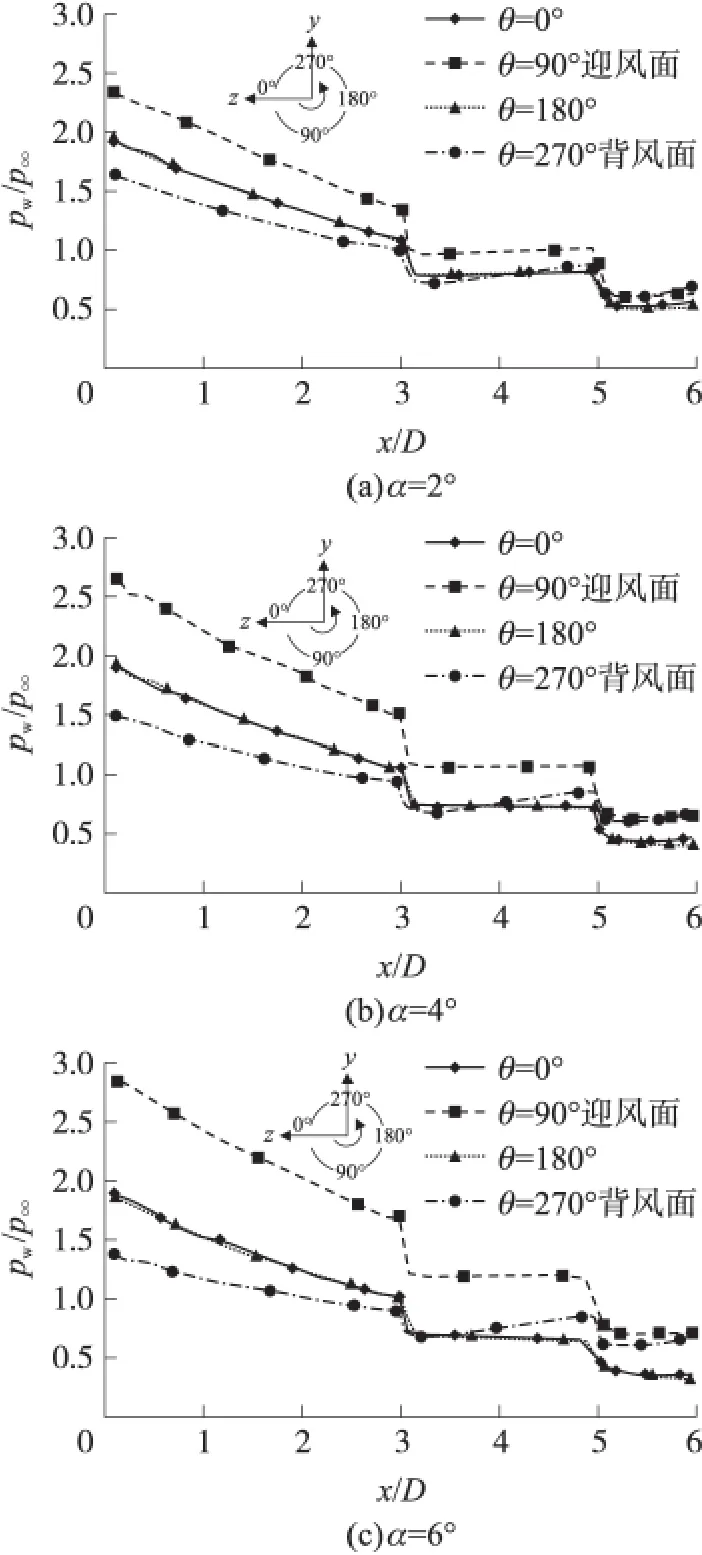
圖14 馬赫數Ma＝3，轉速Ω＊＝0.19時彈丸的表面壓力分布

從圖14可以看出，隨著攻角的增大，可以發現除了彈尾部，其他部位壓力值很接近，說明彈尾部的壓力差值是導致馬格努斯現象的主要因素；隨著攻角的增大，彈尾部兩側壓力值是逐漸減小的，但是它們之間的壓力差值是逐漸增大的，這說明壓力減小了，但是馬格努斯力和馬格努斯力矩是增大的。同時從圖3可以看出，隨著攻角的增大，馬格努斯力和馬格努斯力矩是逐漸增大的，這個現象說明彈尾部是產生馬格努斯現象的主要部位，并且馬格努斯效應對彈丸的影響隨著攻角的增大而越來越明顯。

2.3 表面壓力分布隨馬赫數的變化

Ω＊＝0.19且α＝6°時，不同馬赫數下彈丸表面的壓力分布如圖15所示。

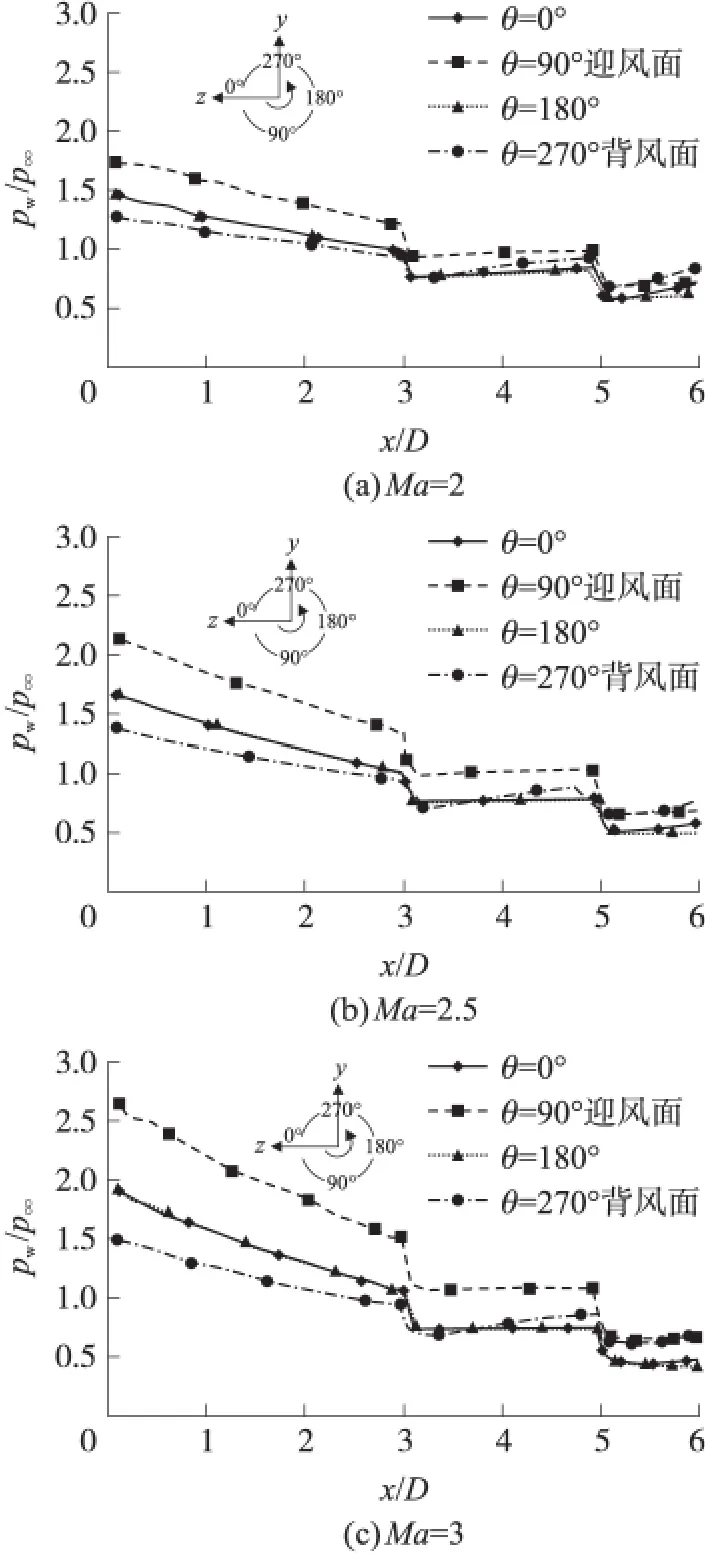
圖15 轉速為Ω＊＝0.19，攻角為6°時的表面壓力分布

從圖15中看到，隨著馬赫數的增大，旋轉彈丸表面的壓力值總體而言都在升高，迎風面和背風面的壓力差顯著變大，勢必導致彈丸的升力升高。觀察背風面和迎風面的壓力分布，可以發現在低馬赫數時，彈尾部會產生與升力方向相反的壓差，顯然這將導致升力減小；隨著馬赫數的增大，壓差值逐漸減小，甚至有壓差反向的趨勢；可以預見，在彈尾部的壓差將導致彈丸的升力減小，但隨著彈丸馬赫數的增大，影響逐漸減小甚至于有促進升力增大的趨勢。再觀察彈尾部表面的壓力會發現，隨著馬赫數的增大，迎風面和背風面的壓力值變化不大；但是觀察彈丸的θ＝0和θ＝180°兩側的壓力值，發現隨著馬赫數的增大，彈尾部的壓力值逐漸減小，更重要的是壓力差值也越來越小，這說明隨著馬赫數的增大，馬格努斯效應對彈丸的影響越來越小。

2.4 馬格努斯力與力矩系數的經驗公式

根據前面的數據，可以得知，在小攻角情況下，馬格努斯系數隨著攻角以及轉速是線性變化的，隨馬赫數呈現冪級數變化；再考慮到當馬赫數、攻角以及轉速的值存在0時，那么馬格努斯系數必為0，因此，本文提出馬格努斯力與力矩系數經驗計算公式：

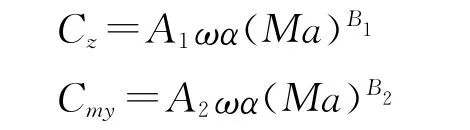
根據馬格努斯系數對攻角以及馬赫數關系曲線，算出A1＝－5.45×10－7，B1＝－1.788；同樣方法求得A2＝2.9×10－6，B2＝－1.896。

將公式應用于轉速為30 000r／min，攻角為6°，Ma＝3工況下，計算馬格努斯系數差百分比分別為

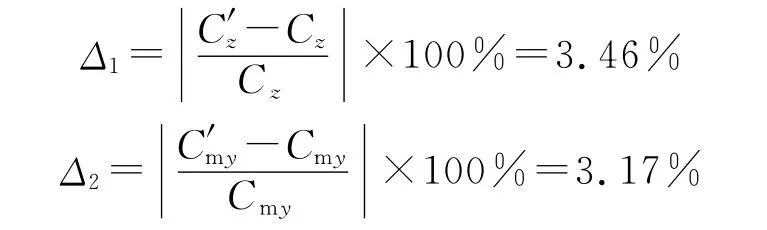
因為偏差的百分比都比較小，可以斷定，在小攻角、超聲速情況下，此經驗公式完全適用，并比先前的經驗公式簡單實用。

3 結束語

本文用軟件對SOCBT彈丸流場進行了數值模擬，分析了彈丸表面壓力分布隨著攻角、馬赫數以及轉速的變化情況。結果表明：旋轉對升阻力影響很小，幾乎可以忽略不計；彈尾部是影響馬格努斯現象的主要部位；隨著攻角的增大，馬格努斯力和馬格努斯力矩系數逐漸增大，在小攻角范圍內呈線性變化，當攻角足夠大后趨于不變；相同轉速和相同攻角情況下，隨著馬赫數的增大，旋轉效應對彈丸的影響越來越小；在其他條件相同時，馬格努斯力與力矩隨著轉速的增加基本呈線性增大。并在上述基礎上，提出并驗證了馬格努斯力與力矩系數計算的經驗公式，適用于小攻角、超聲速情況的計算。

［1］韓子鵬.彈箭外彈道學［M］.北京：北京理工大學出版社，2008.HAN Zi－peng.External ballistics of projectiles and missiles［M］.Beijing：Beijing Institute of Technology Press，2008.（in Chinese）

［2］于劍橋，別炎華.滾轉導彈動態失穩的機理分析［J］.彈道學報，2008，20（2）：24－26.YU Jian－qiao，BIE Yan－hua.Mechanism analysis on dynamic instability of rolling missile［J］.Journal of Ballistics，2008，20（2）：24－26.（in Chinese）

［3］閆曉勇，張成，楊樹興.一類滾轉彈的補償解耦方法［J］.彈道學報，2009，21（4）：17－20.YAN Xiao－yong，ZHANG Cheng，YANG Shu－xing.Decoupling technique for a class of rolling missile［J］.Journal of Ballistics，2009，21（4）：17－20.（in Chinese）

［4］張煥好，陳志華，姜孝海，等.高速彈丸穿越不同制退器時的膛口流場波系結構研究［J］.兵工學報，2012，33（5）：623－629.ZHANG Huan－hao，CHEN Zhi－hua，JIANG Xiao－hai，et al.Investigation on the blast wave structures of a high－speed projectile flying through different muzzle brakes ［J］.Acta Armamentarii，2012，33（5）：623－629.（in Chinese）

［5］SILTON S I.Navier－Stokes computation for a spinning projectile from subsonic to supersonic speeds，AIAA 2003－3936［R］.2003.

［6］DESPIRITO J，HEAVEY K R.Heavey.CFD computation of Magnus moment and roll damping moment of a spinning projectile，AIAA 2004－4713［R］.2004.

［7］DESPIRITO J，PLOSTINS P.CFD prediction of M910projectile aerodynamics：unsteady wake effect on Magnus moment，AIAA 2007－6580［R］.2007.

［8］PECHIER M，GUILEN P.A combined theoretical experimental investigation of Magnus effects，AIAA 98－2797［R］.1998.

［9］DESPIRITO J.CFD prediction of Magnus effect in subsonic to supersonic flight，AIAA 2008－427［R］.2008.

［10］雷娟棉，李田田，黃燦.高速旋轉彈丸馬格努斯效應數值研究［J］.兵工學報，2013，34（6）：718－725.LEI Juan－mian，LI Tian－tian，HUANG Can.A numerical investigation of Magnus effect for high－speed spinning projectile［J］.Acta Armamentarii，2013，34（6）：718－725.（in Chinese）