基于Johnson－Cook本構(gòu)模型的彈帶擠進過程數(shù)值模擬

王 鵬，楊國來，葛建立，孫全兆，梁傳建

（南京理工大學(xué) 機械工程學(xué)院，南京210094）

對于火炮的內(nèi)彈道而言，彈帶擠進是一個很重要的過程。該過程直接改變膛內(nèi)容積的變化規(guī)律，對膛內(nèi)火藥氣體生成速率、膛內(nèi)壓力的變化、火炮初速的大小產(chǎn)生重要影響，而且與身管壽命、射擊密集度以及射擊安全性等火炮武器關(guān)鍵性能指標密切相關(guān)［1］。然而，傳統(tǒng)內(nèi)彈道理論一般忽略擠進過程，認為該過程瞬間完成。彈丸擠進過程實際是彈帶和身管內(nèi)膛發(fā)生接觸碰撞，膛線逐漸侵徹彈帶，彈帶材料不斷失效和破壞的過程，具有高瞬時、強沖擊、高溫變、高速變的特點，擠進阻力和變形的規(guī)律十分復(fù)雜［2－3］。由于具有諸多難點，目前現(xiàn)有的研究理論與實際擠進過程仍有較大差距，亟需針對擠進過程展開研究工作。

本文以某大口徑火炮彈帶擠進過程為研究對象，開展其非線性動力學(xué)建模與數(shù)值計算研究，提出運用Johnson－Cook本構(gòu)關(guān)系模型描述材料變形和失效問題，建立精確的彈帶擠進過程模型，重點針對該大口徑火炮發(fā)射條件下彈帶擠進過程的彈帶大變形問題、彈丸運動規(guī)律、擠進壓力、擠進阻力變化規(guī)律進行數(shù)值計算研究，并分析摩擦性質(zhì)對擠進過程的影響。

1 Johnson－Cook本構(gòu)關(guān)系模型

材料本構(gòu)關(guān)系是材料變化的體現(xiàn)與描述，本構(gòu)關(guān)系體現(xiàn)了材料在外界作用下發(fā)生變形，強度隨著應(yīng)變及溫度等因素改變的情況，在有限元建模仿真中具有重要的地位。

在大口徑火炮射擊時，彈丸擠進膛線的過程是一個復(fù)雜的材料塑性流動過程。本文研究的彈帶材料為紫銅，彈帶在擠進過程中經(jīng)歷彈塑性大變形及損傷，最終發(fā)生韌性斷裂，涉及到彈帶材料的應(yīng)變硬化、應(yīng)變率硬化和溫度軟化，可采用Johnson－Cook塑性及斷裂失效模型［4－5］。

Johnson－Cook本構(gòu)關(guān)系模型（簡稱J－C模型）是一個經(jīng)驗性的粘塑性模型，是由Johnson和Cook于1983年提出的用于高應(yīng)變率和高溫情況下的本構(gòu)關(guān)系模型［4］，形式簡單，使用方便，在沖擊動力學(xué)中得到了廣泛應(yīng)用。該模型由兩部分組成。

第一部分為應(yīng)力－應(yīng)變關(guān)系，表示為

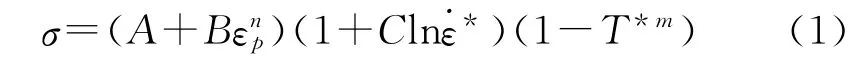
式中：σ為von Mises屈服應(yīng)力；A為準靜態(tài)實驗下的屈服強度；B，n為應(yīng)變強化參數(shù)；C為經(jīng)驗性應(yīng)變率敏感系數(shù)；m為溫度軟化指數(shù)；εp為等效塑性應(yīng)變?yōu)闊o量綱的等效塑性應(yīng)變率。相對溫度：

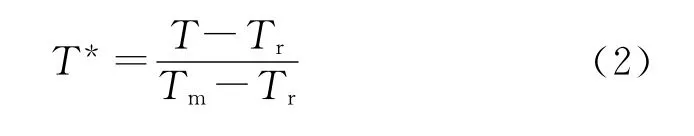
式中：Tr為參考溫度（一般取為室溫），Tm為常態(tài)下材料的熔化溫度。

第二部分為斷裂時的應(yīng)變：

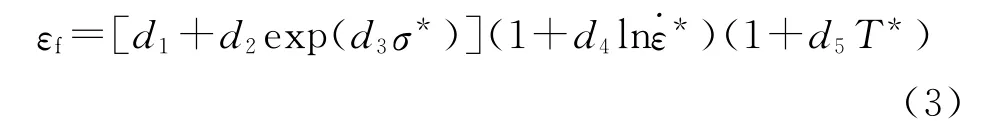
式中：應(yīng)力三軸度σ＊＝p／σeff，p為靜水應(yīng)力，σeff為等效應(yīng)力；d1，d2，d3，d4，d5分別為材料參數(shù)，由試驗測試確定。

材料的失效由塑性應(yīng)變累積準則來判斷：

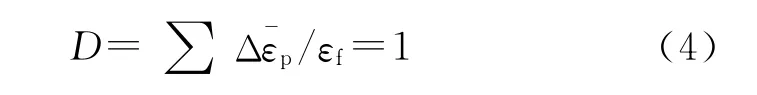
擠進過程涉及的紫銅、炮鋼材料參數(shù)見表1，表中ρ、E、ν分別為密度、彈性模量與泊松比。

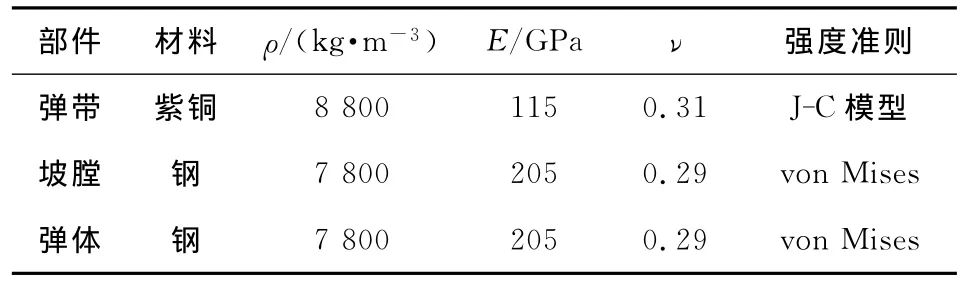
表1 擠進系統(tǒng)主要材料力學(xué)性能

確定彈帶材料紫銅的Johnson－Cook模型參數(shù)，對于準確模擬擠進過程非常重要。紫銅是廣泛使用的傳統(tǒng)工業(yè)材料，可在參考文獻［4－5］中引用現(xiàn)成的本構(gòu)模型參數(shù)，由表2列出。

表2 紫銅材料Johnson－Cook本構(gòu)關(guān)系參數(shù)

2 擠進模型的建立

2.1 擠進過程建模基本假設(shè)

彈丸擠進過程的受力和變形情況非常復(fù)雜，具有高瞬時、強沖擊、大變形、高速變的特點。為了提高所建模型的仿真效果，忽略次要的影響因素，對彈帶擠進內(nèi)膛過程作如下基本假設(shè)［6］：

①由于擠進過程非常短暫，故假定擠進過程是在室溫情況下的絕熱沖擊過程；

②卡膛到位后，認為彈帶和坡膛傾角緊密配合，并將此位置作為彈丸擠進過程的開始；

③忽略不均衡問題，假定彈丸與身管軸線共心，摩擦力與運動阻力都沿軸線方向；

④忽略彈丸前部的空氣阻力和激波的影響；

⑤忽略彈帶的初始應(yīng)力及有關(guān)溫度等影響；

⑥不考慮身管的后坐運動。

2.2 擠進系統(tǒng)的網(wǎng)格劃分

在擠進系統(tǒng)的模型網(wǎng)格劃分中，對于重點考察研究的彈帶等部位，盡量將網(wǎng)格精細化處理，并采用ALE自適應(yīng)網(wǎng)格技術(shù)，選擇C3D8R（8節(jié)點減縮積分單元）作為劃分的網(wǎng)格單元類型。為減少計算時間，對于彈體、膛線和身管等部位，用分割網(wǎng)格的方法以減小總體網(wǎng)格模型的規(guī)模。圖1、圖2為建立的網(wǎng)格模型。

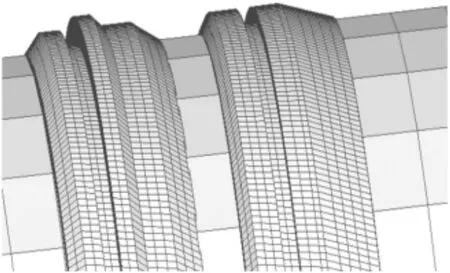
圖1 彈帶和彈丸網(wǎng)格劃分

圖2 膛線和身管網(wǎng)格劃分

各部分網(wǎng)格數(shù)量見表3所示。

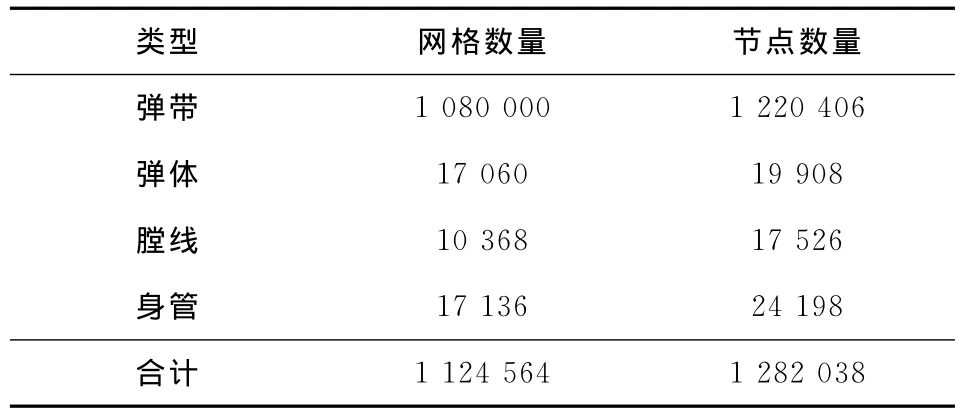
表3 各部分網(wǎng)格與節(jié)點數(shù)量

2.3 載荷和邊界條件

彈底壓力是彈丸所受到的最主要作用力，是推動彈丸向前運動的動力。通過實彈射擊測試得到該大口徑火炮最大號裝藥條件下擠進時期膛底壓力變化曲線，由文獻［1］所述內(nèi)彈道計算中應(yīng)用的壓力換算關(guān)系式（5），換算得到彈底壓力，如圖3所示。

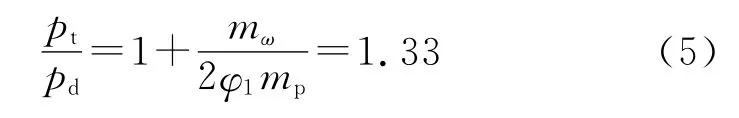
式中：pd為彈底壓力；pt為膛底壓力；mp為彈丸質(zhì)量；mω為發(fā)射藥質(zhì)量；φ1為次要功系數(shù)。

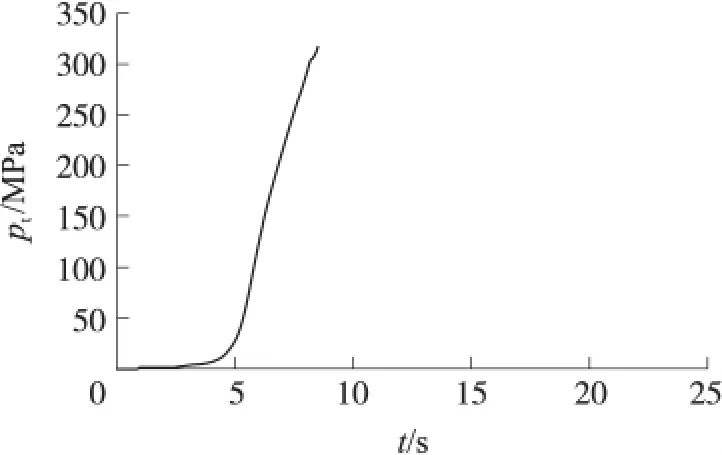
圖3 膛內(nèi)壓力曲線數(shù)據(jù)

將轉(zhuǎn)換得到的彈底壓力作為彈底載荷條件。邊界條件對彈體沒有任何約束，對身管作全約束。

3 數(shù)值仿真計算及結(jié)果分析

將建立好的擠進系統(tǒng)模型提交ABAQUS運算，得到擠進數(shù)值模擬結(jié)果，重點針對彈丸擠進過程中彈帶變形和刻痕的形成過程、擠進過程彈丸運動規(guī)律、彈帶動態(tài)擠進阻力、擠進壓力進行分析。

3.1 彈帶變形及刻槽形成過程

彈帶槽的形成過程是擠進過程研究中一個比較關(guān)心的問題。利用ABAQUS／Explicit進行數(shù)值計算，得到彈帶擠進膛線的變化過程。按照擠進進程的時間先后，用明顯變形后的網(wǎng)格圖來顯示彈帶槽的形成過程，如圖4所示。

圖4（a）示意在t＝3.0ms時刻之前，彈帶變形一直處于較低的水平，也就是說此時刻以前，彈帶只發(fā)生了彈性變形，還沒有出現(xiàn)材料的斷裂破壞；圖4（b）顯示，t＝4.0ms時彈帶網(wǎng)格的部分區(qū)域發(fā)生材料失效斷裂，彈帶已顯現(xiàn)出變形刻槽；圖4（c）顯示t＝5.0ms時刻第一條彈帶部分已經(jīng)出現(xiàn)斷裂刻槽，彈帶已經(jīng)被明顯切削擠進；圖4（d）顯示了t＝6.0ms時刻第一條彈帶即將切削完畢的情況；圖4（e）顯示t＝6.5ms時第二條彈帶前部被擠壓變形的情況；圖4（f）顯示t＝7.0ms時第二條彈帶進一步被擠壓的情況；圖4（g）顯示t＝7.5ms時第二條膛線整體即將被切削完畢的情況；圖4（h）顯示了t＝8.0ms時擠進完成后的彈帶網(wǎng)格圖，刻槽形成。

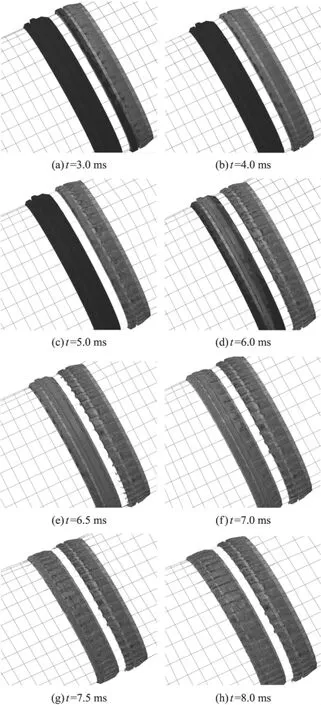
圖4 擠進過程中不同時刻彈帶網(wǎng)格變形圖

通過以上彈帶網(wǎng)格變形圖，可以看出，彈帶在擠進過程中不斷發(fā)生材料失效，最終被切削成刻槽。通過與實彈射擊回收得到的彈帶外形（如圖5所示）對比，數(shù)值模擬和實彈射擊得到的彈帶外形基本一致。

圖5 射擊后的切削彈帶

3.2 彈丸運動規(guī)律

根據(jù)上文中關(guān)于擠進模型的基本假設(shè)，取模型中彈丸質(zhì)心位置的節(jié)點，可得彈丸的運動變化規(guī)律。

如圖6～圖8所示，分別為擠進模型數(shù)值模擬計算得到的彈丸質(zhì)心位移（s）－時間曲線、速度（v）－時間曲線和加速度（a）－時間曲線。

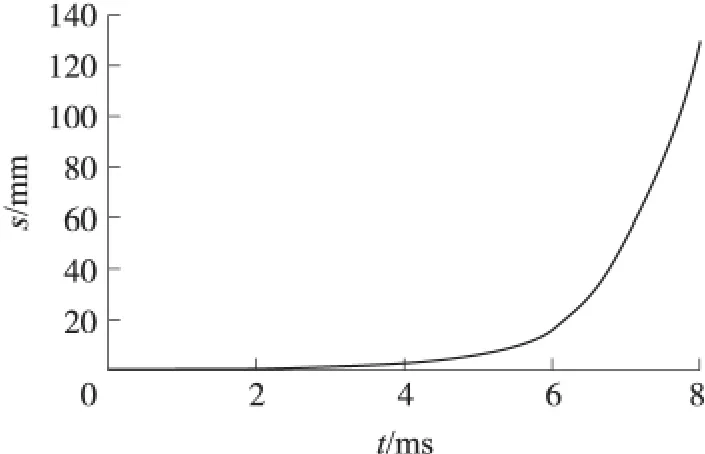
圖6 彈丸質(zhì)心運動位移－時間曲線

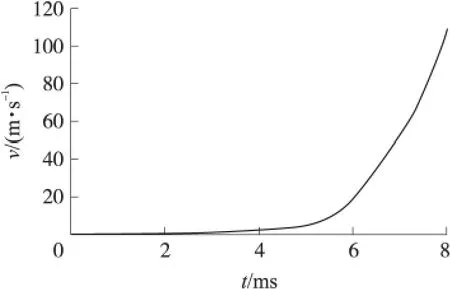
圖7 彈丸質(zhì)心運動速度－時間曲線

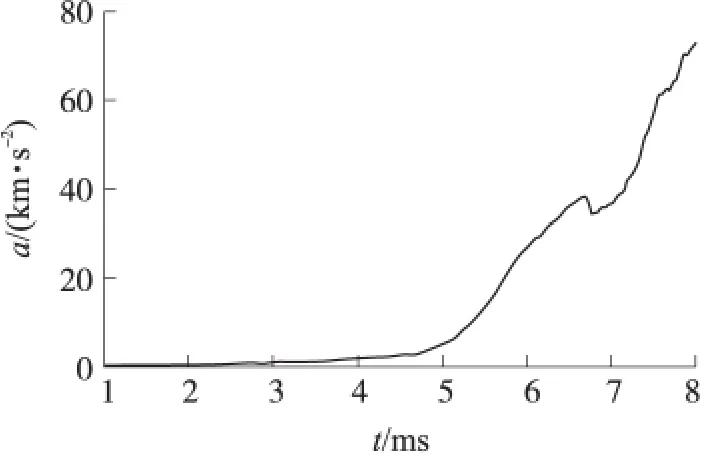
圖8 彈丸質(zhì)心加速度－時間曲線

分析圖6可知：彈丸在2.92ms時刻前位移為0mm，將該時刻作為彈丸開始運動時間，即t1＝2.92ms。該時刻以后，彈丸開始移動；并且隨著時間的增加，位移增長的速率不斷增加。

分析圖7可知：彈丸在2.92ms前速度基本為0；2.92ms時刻以后，彈丸速度開始增加，說明開始移動，并隨著時間的增加，速度增長的速率不斷增加。

分析圖8可知：在前2.92ms時間內(nèi)彈丸加速度基本為0；2.92ms時刻后彈丸開始逐漸出現(xiàn)加速度，并且隨著彈底加速度上升而迅速上升；6.74ms時刻出現(xiàn)下降沿，原因是擠進阻力的增加速率超過了彈底壓力的速率；隨著壓力的增加，7.02ms時刻后加速度重新呈現(xiàn)增長趨勢。

3.3 彈帶擠進阻力變化

本文提出一種實用的擠進阻力求解方法，針對彈丸膛內(nèi)軸向受力情況，根據(jù)牛頓第二定律，可得到擠進過程運動方程：

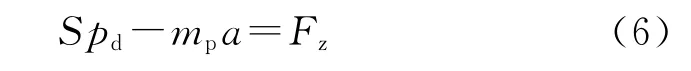
式中：Fz為擠進阻力，S為彈底面積，mp為彈丸質(zhì)量；a為彈丸加速度。代入上文得到的加速度變化規(guī)律，即可得到彈帶擠進阻力－時間曲線，如圖9所示。

為清晰起見，圖9給出擠進阻力明顯增加階段的擠進阻力－時間曲線。隨著彈帶變形程度增加，變形阻力逐漸增大；到7.14ms時刻擠進阻力達到最大值，對應(yīng)的最大擠進阻力為1 420kN。達到最大值后，彈帶變形量逐漸減小，擠進阻力逐漸降低，達到某值后保持穩(wěn)定，說明已經(jīng)擠進完成。

圖9 擠進阻力－時間曲線

文獻［7］描述了美國某155mm榴彈炮運動阻力曲線，如圖10所示。該曲線中，位移40mm處出現(xiàn)最大擠進阻力為1 040kN，該結(jié)論與本文計算結(jié)果數(shù)量級相當(dāng)并數(shù)值接近。

該火炮阻力曲線與本文得到的曲線變化規(guī)律相近，彈底壓力增大到一定值后，彈丸才開始運動；彈帶變形量不變時，擠進阻力也會保持穩(wěn)定；彈丸擠進完成后阻力下降并保持在一定值。這些研究結(jié)論的吻合也佐證本文結(jié)論的正確性。

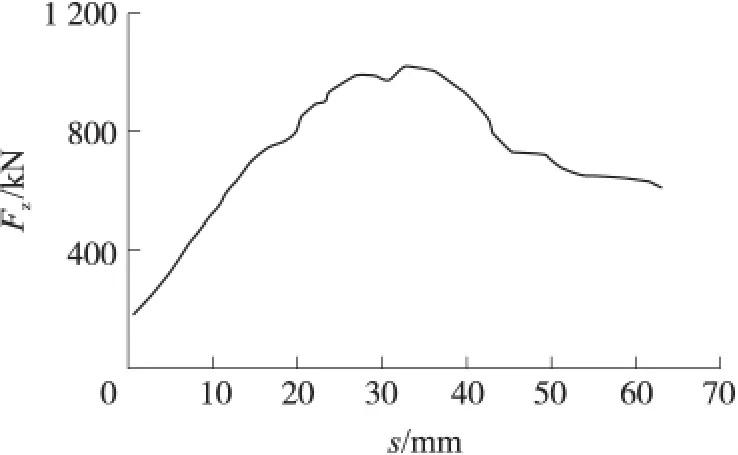
圖10 美155mm榴彈炮彈帶擠進阻力變化

3.4 啟動壓力與擠進壓力

文獻［8］中作了如下定義：啟動壓力是指彈丸開始運動瞬間對應(yīng)的火藥氣體平均壓力；擠進壓力指在彈帶全部擠進膛線瞬間與之相應(yīng)的彈后火藥氣體燃氣的平均壓力。

由上節(jié)論述，彈丸開始運動時間t1＝2.92ms，該時間對應(yīng)的火藥氣體平均壓力為11.4MPa，即彈丸啟動壓力為11.4MPa。

對于該大口徑火炮，彈帶完全擠進膛線需要的行程為98mm。由彈丸位移－時間曲線，位移為98mm對應(yīng)的時刻為7.68ms，該時刻對應(yīng)的火藥氣體平均壓力為243.9MPa，即擠進壓力為243.9MPa。

對應(yīng)的彈丸速度為98.2m／s，該大口徑火炮初速為1 050m／s，即擠進完成時彈丸速度已經(jīng)達初速的9.4%。內(nèi)彈道過程中最大膛壓為374.6MPa，擠進壓力為最大膛壓的65.16%。

將計算得到的結(jié)果歸納，得表4，表中t、p′、s、v分別為時間、膛內(nèi)火藥燃氣壓力、彈丸行程與彈丸速度。

對從彈丸啟動瞬間時刻t1至擠進阻力達最大時刻t2的火藥氣體壓力積分，并求取平均值：

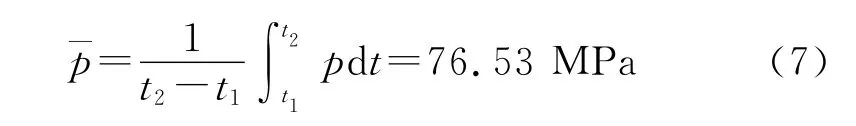
式中：p為膛內(nèi)火藥燃氣平均壓力。

這與傳統(tǒng)內(nèi)彈道計算初始條件通常取為30MPa是有明顯差異的。

以上這些結(jié)論與前人的一些研究結(jié)論是相當(dāng)吻合的。文獻［9］的研究發(fā)現(xiàn)：擠進終了時的燃氣壓力遠大于瞬時擠進所采用的30MPa，擠進完成時的擠進壓力為最大膛壓的65%；擠進過程所需要的時間為火藥全部燃燒完時間的25%～33%，且擠進瞬間已經(jīng)燃燒去火藥的10%～15%；擠進完成瞬時彈丸速度已達初速的10%。文獻［10］通過測試得到射擊條件下采用銅彈帶的海30炮擠進壓力為209MPa，計算值為201.3MPa，本文計算結(jié)果與之在數(shù)量級上也相當(dāng)。

這些文獻結(jié)論可以從一些方面佐證本文數(shù)值模擬結(jié)果的合理性，但若要精確的驗證，需要對該大口徑火炮進行試驗測試，這些將在下一步工作中進行。

4 摩擦性質(zhì)對擠進過程的影響

彈帶內(nèi)膛之間的摩擦阻力與彈帶塑性變形阻力是彈帶擠進阻力的2個重要組成部分。當(dāng)彈丸開始運動后，彈帶與坡膛、膛線開始接觸碰撞變形，這個過程中所引起的正壓力是很大的。而摩擦阻力的大小取決于正壓力和摩擦系數(shù)，故在正壓力很大的情況下，摩擦系數(shù)對擠進阻力的影響是顯著的。

4.1 不同摩擦性質(zhì)下擠進變化

為了研究彈丸在不同摩擦性質(zhì)下的擠進變化規(guī)律，分別建立了某大口徑火炮在摩擦阻力系數(shù)μ分別為0，0.05，0.1，0.15 4種不同摩擦性質(zhì)下的擠進模型，并分別計算出不同摩擦性質(zhì)下的擠進過程變化，表5列出了不同摩擦性質(zhì)下的擠進過程計算結(jié)果，表中t0、Fzm、p0分別為擠進完成時刻、最大擠進阻力與擠進壓力。

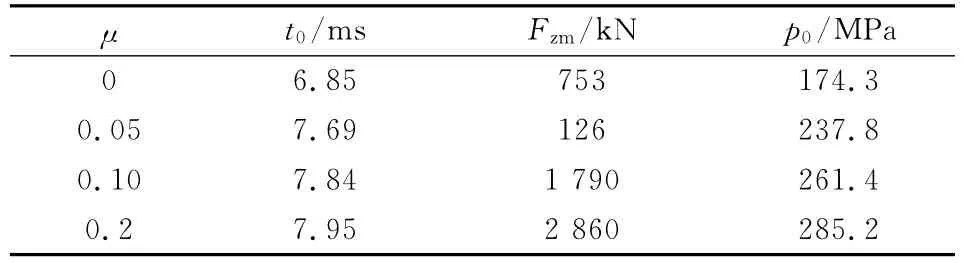
表5 不同摩擦性質(zhì)下擠進過程變化

可以看出，摩擦阻力變大，擠進時間越長，擠進阻力越大，對應(yīng)的擠進壓力也就越大。相反，摩擦阻力變小，擠進就越容易，時間越短，相應(yīng)的擠進壓力也會降低。

4.2 “首發(fā)近彈”原因的簡單討論

現(xiàn)役火炮在實彈射擊時，往往會出現(xiàn)“首發(fā)近彈”現(xiàn)象，即第一發(fā)射彈的實際射程要比預(yù)定的射程近一定距離。

本文嘗試從擠進的角度去分析首發(fā)近彈產(chǎn)生的原因。經(jīng)驗表明，火炮在每天第1發(fā)射擊時出現(xiàn)首發(fā)近彈的現(xiàn)象。通過對同一天各發(fā)的射擊過程和射擊條件進行跟蹤，發(fā)現(xiàn)一個明顯特征是每天首發(fā)射擊時炮膛內(nèi)有油，其后的各發(fā)膛內(nèi)沒有油。正常情況下，紫銅彈帶與炮鋼間的摩擦系數(shù)一般取為0.19左右，火炮在實彈射擊前，都要進行正常的維護與保養(yǎng)，擦拭炮膛，涂抹炮油，會將摩擦系數(shù)降低到0.05以下。首發(fā)射擊后，高速、高溫、高壓的膛內(nèi)火藥氣體會把膛內(nèi)表面的涂油燃燒掉，而后進行射擊的各發(fā)是內(nèi)膛表面無油條件下的彈帶擠進過程，彈丸的運動壓力、彈道性能也均恢復(fù)到正常狀態(tài)，不會再發(fā)生近彈的現(xiàn)象。

表6為首發(fā)射擊與第2發(fā)射擊擠進變化對比。首發(fā)炮彈由于油膜層的作用，初始摩擦系數(shù)為0.04，計算后得到擠進完成時刻為7.20ms，對應(yīng)的擠進壓力為212.9MPa；第2發(fā)彈初始摩擦系數(shù)恢復(fù)到0.19，計算得到擠進完成時刻為7.47ms，對應(yīng)的擠進壓力為275.4MPa。

表6 首發(fā)射擊與第2發(fā)射擊擠進變化對比

同時，首發(fā)彈比第2發(fā)彈的啟動壓力要小，即彈丸在較低的壓力下就開始運動，這會明顯地影響到點傳火和火藥燃燒過程，使最大膛壓變低，彈丸初速變小，從而導(dǎo)致“首發(fā)近彈”現(xiàn)象發(fā)生。

5 結(jié)束語

本文以某大口徑火炮彈帶擠進過程為研究對象，采用Johnson－Cook本構(gòu)模型描述了材料的破壞失效，結(jié)合實驗測試數(shù)據(jù)在有限元軟件ABAQUS中建立了擠進過程的非線性動力學(xué)模型，利用顯式數(shù)值積分算法對彈帶擠進過程的非線性動力學(xué)進行了數(shù)值模擬。重點針對該大口徑火炮發(fā)射條件下彈帶擠進過程的彈帶刻槽形成過程、彈丸擠進運動規(guī)律、擠進阻力動態(tài)變化、擠進壓力進行了研究，并探討了摩擦性質(zhì)對彈帶擠進過程的影響，主要得到了以下結(jié)論：

①采用Johnson－Cook本構(gòu)模型，較好地描述了彈帶材料不斷變形、斷裂失效，得到了彈帶刻槽形成過程。

②通過數(shù)值計算得到了彈丸擠進運動規(guī)律、擠進阻力動態(tài)變化規(guī)律，以及確定了啟動壓力與擠進壓力，并論證了結(jié)果的可信性。

③得到了摩擦阻力對擠進過程的影響，摩擦系數(shù)越大，擠進時間越長，擠進阻力越大，對應(yīng)的擠進壓力也就越高；并從這一角度對“首發(fā)近彈”現(xiàn)象做出了解釋。

［1］錢林方.火炮彈道學(xué)［M］.北京：北京理工大學(xué)出版社，2009：145－147.QIAN Lin－fang.Ballistics of guns［M］.Beijing：Beijing Institute of Technology Press，2009：145－147.（in Chinese）

［2］樊黎霞，何湘玥.彈丸擠進過程的有限元模擬與分析［J］.兵工學(xué)報，2011，32（8）：963－969.FAN Li－xia，HE Xiang－yue.Finite element simulation and process analysis of projectile entering into barrel［J］.Acta Armamentarii，2011，32（8）：963－969.（in Chinese）

［3］陸野，周克棟，赫雷，等.某大口徑槍械內(nèi)彈道擠進時期的數(shù)值仿真與分析［J］.彈道學(xué)報，2014，26（2）：67－71.LU Ye，ZHOU Ke－dong，HE Lei，et al.Numerical simulation and analysis of engraving duration during interior ballistics of some large－caliber small arms［J］.Journal of Ballistics，2014，26（2）：67－71.（in Chinese）

［4］JOHNSON G R，COOK W H.A constitutive model and data for metals subjected to large strains，high strain rates and high temperatures［C］／／Proceedings of the 7th International Symposium on Ballistics.Hague：IBC，1983：541－547.

［5］JOHNSON G R，COOK W H.Fracture characteristics of three metals subjected to various strains，strain rates，temperatures and pressures［J］.Engineering Fracture Mechanics，1985（21）：31－48.

［6］張振輝.末制導(dǎo)炮彈與火炮身管相互耦合機理及適配性技術(shù)［D］.南京：南京理工大學(xué)，2013：47－51.ZHANG Zhen－h(huán)ui.Suitability technology and inter－coupling mechanism of guided projectile entering into barrel［D］.Nanjing：Nanjing University of Science and Technology，2013：47－51.（in Chinese）

［7］張喜發(fā)，盧興華.火炮燒蝕內(nèi)彈道學(xué)［M］.北京：國防工業(yè)出版社，2001：44－45.ZHANG Xi－fa，LU Xing－h(huán)ua.Interior ballistics of erosion guns［M］.Beijing：National Defense Industry Press，2001：44－45.（in Chinese）

［8］金志明.槍炮內(nèi)彈道學(xué)［M］.北京：北京理工大學(xué)出版社，2011：57－58.JIN Zhi－ming.Interior ballistics of guns［M］.Beijing：National Defense Industry Press，2011：57－58.（in Chinese）

［9］丘爾巴諾夫E B.擠進時期內(nèi)彈道學(xué)與擠進壓力計算［M］.楊敬榮，譯.北京：國防工業(yè)出版社，1997：8－20.

［10］何勇.擠進過程實驗研究［J］.彈道學(xué)報，1996，8（4）：33－36.HE Yong.Experimental research of engraving process［J］.Journal of Ballistics，1996，8（4）：33－36.（in Chinese）