彈目交會可視化命中點參數的精確計算

陳 峰，盧旭東，丁 勇

（沈陽理工大學1.裝備工程學院；2.信息工程學院 沈陽110159）

引戰配合是武器系統中的一個重要環節，目的是使戰斗部最大程度地殺傷目標。近些年隨著目標導彈的復雜性提高和數字計算機技術特別是高分辨率顯卡技術的快速發展，計算機可視化仿真成為研究引戰配合問題的重要手段。傳統的仿真系統一般通過概率密度積分的方法求解命中點的參數［1－3］，此方法計算精度較差，而且無法精確計算破片命中點的坐標、命中數目、落角、擊中動能等。王宏波等［4］基于目標三維實體模型提出了一種計算命中點參數的方法，但是未能考慮破片的速度衰減對命中點參數的影響，且該方法在程序的每個時間步長內要對所有的命中點進行遍歷判斷，導致程序的執行效率不高。王馬法等［5］給出了破片命中點參數的理論計算模型，但是對命中點參數并沒有給出具體的仿真實例進行驗證。

本文基于三維可視化仿真系統，對破片命中點參數算法進行了深入的研究，在地面坐標系下，綜合考慮了不同高度的大氣壓強和溫度等因素對破片速度的影響。將破片的運動軌跡視作一條3D射線（通稱Ray射線，具體參見下文），局部遍歷求解命中點參數，即先為每個破片創建一個包圍球［6－7］，為目標模型的每個部件創建各自的包圍球，遍歷檢測破片包圍球與目標模型的全局包圍球的碰撞是否相交；若相交，再檢測破片的包圍球，遍歷與模型的各部件包圍球的碰撞是否相交。之后通過程序存儲發生碰撞的目標模型部件，同時將此時發生碰撞的每個破片包圍球的方向矢量賦值給每條3D射線，局部遍歷檢測每條3D射線與所存儲包圍球的碰撞，存儲目標模型部件三角形面元命中點參數。本文仿真實例表明：該算法極大地提高了程序的執行效率，計算精度更高（可遍歷目標部件更多的三角形面元）；有效地避免了傳統算法因三角形數目過多導致計算量更大的不足；所得到的命中點參數數據對引戰配合中毀傷概率的研究具有一定的參考價值。

1 目標模型

通過3DSMax建立目標三維幾何模型（包括所需的各種紋理材質等），之后導入到XNA（Xbox／DirectX New Generation Architecture，基 于 DirectX游戲開發環境）［8－9］，圖1所示為目標模型和目標面元模型。

圖1 目標導彈模型

在XNA中，首先導出目標模型所有的頂點位置坐標，存儲目標模型各部件的三角形面元頂點信息，即以模型各個組成的部件為單元，采用分別定義的三角形集合存儲每個部件的三角形面元信息。算法如下：

for（inti＝0；i＜TranagleNum；i＋＋）

｛ int index 0＝arrayMeshIndices［3＊i＋0］；

int index 1＝arrayMeshIndices［3＊i＋1］；

int index 2＝arrayMeshIndices［3＊i＋2］；

Vector 3v0＝arrayMeshVertices［index 0］；

Vector 3v1＝arrayMeshVertices［index 1］；

Vector 3v2＝arrayMeshVertices［index 2］；

Triangle hisNewTriangle＝new Triangle （v0，v1，v2）；

Meshtriangle.Add（hisNewTriangle）； ／／ ｝其中：參數i表示該目標面元每個三角形面元的信息；TriangleNum為模型每個部件的三角形面元的數目；arrayMeshIndices為每個部件頂點的索引數組；每 個 三 角 形 面 元 頂 點 為vi0（v0x，v0y，v0z），vi1（v1x，v1y，v1z），vi2（v2x，v2y，v2z），即每個三角形在地面坐標系中頂點的坐標值；hisNewTriangle為模型部件中每個三角形位置信息；Meshtriangle為模型每個部件三角形面元信息的集合數組。

2 破片命中點參數計算模型

本文的破片命中參數計算模型分成2部分，即破片包圍球碰撞檢測模型和檢測后的破片Ray射線命中點參數計算模型。這里用球形破片近似代表模型的破片，通過給出戰斗部靜止狀態下爆炸后產生破片群的空間飛散規律以及破片的初始速度，得出戰斗部動態爆炸時破片動態的飛散特性。破片在動態飛散角內近似服從正態分布，算法很成熟，這里不再詳述［10－11］

2.1 破片的包圍球碰撞檢測模型

在戰斗部動態爆炸時，為每個破片和目標模型的各個部件創建各自的包圍球，包圍球的運動軌跡方程與所對應的動態破片運動方程一樣。下面介紹破片包圍球碰撞檢測的計算模型。

如圖2（a）所示，在3DSMax中建模時，目標模型由多個部件構成。在將模型導成供XNA調用的X文件后，在XNA中通過調用函數庫中的骨骼矩陣將模型的各部分連接起來并在屏幕中進行顯示。調用 XNA中BoundingSphere.CreateMerged（組合）方法將圖2（a）中的模型各個部件的包圍球組合成模型的全局包圍球，如圖2（b）所示。同理，創建破片的包圍球（由于破片在建模時已經用球形破片代替，建模時破片只由一個部件構成，所以破片的部件包圍球也為破片的全局包圍球）。由于其原理與目標模型的包圍球相同，這里不再給出破片包圍球的示意圖。

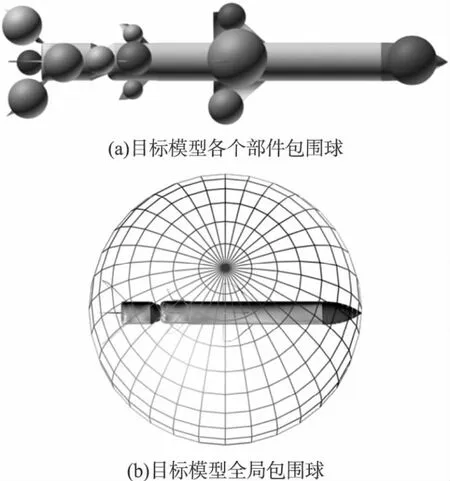
圖2 目標模型的各部件包圍球和全局包圍球示意圖

戰斗部爆炸后，在地面坐標系，假設目標作勻速直線運動，破片的運動為一條射線，故起始階段破片的包圍球的運動方程為

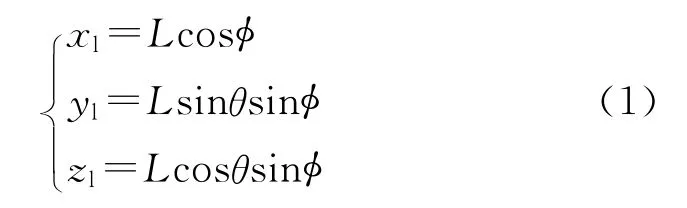
式中：φ為飛散方向角，θ為位偏角，L表示包圍球在空中飛行的距離。破片在飛行的過程中會受到空氣阻力和重力的作用，由于破片的速度較高、質量較小，因此這里忽略重力的影響。空氣阻力使破片的速度減小，衰減過程與空氣的密度、破片的迎風面積以及阻力系數有關，根據牛頓運動定律，其運動微分方程為

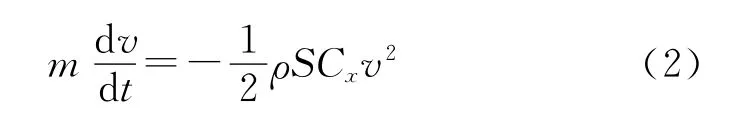
式中：m為破片的質量；ρ為空氣密度；v為破片的速度；Cx為空氣阻力系數；S為破片的迎風面積，對于直徑為D的球形破片，S＝πD2／4。當破片的初速和飛行距離為v0和x時，由式（2）得到破片的運動衰減特性方程：

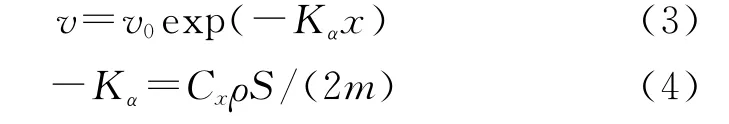
式中：Kα為破片的速度衰減系數，表征破片飛行過程中保存速度的能力。式（4）表明，破片的衰減系數與自身的質量、空氣密度及空氣阻力系數有關（空氣阻力系數為馬赫數的函數，經查閱相關資料，空氣阻力系數近似取值為0.97）。由理想氣體狀態方程知，空氣密度是壓力和溫度的函數，即

式中：R為氣體常數，其值為287.04J／（kg·K）；p為壓強；T為溫度。p，T均為破片飛行高度的函數，空氣壓強、密度和溫度的變化均為破片飛行高度的函數，所參照的標準大氣壓為0.1MPa，標準溫度為288.9K。上述參數的詳細求解方程見文獻［12－13］。

在動態破片的分散區和破片速度衰減的條件下研究各個破片包圍球的碰撞檢測，即在戰斗部爆炸后，首先遍歷破片包圍球與目標模型的全局包圍球的碰撞檢測，這里調用XNA中的BoundingSphere.Intersects的方法檢測破片的包圍球和模型的全局包圍球是否相交。若相交，再遍歷此時該破片的包圍球和模型各個部件包圍球的碰撞檢測。若破片的包圍球與模型部件的包圍球相交，此時記錄破片的速度并將該速度轉換成一條Ray射線，并同時存儲模型部件中所有的三角形面元。之后用該Ray射線遍歷模型部件的所有三角形面元精確求解破片的命中參數。由于目標模型部件的包圍球數量有限，這樣就不需要破片從戰斗部爆炸開始就遍歷目標三角形面元，而是先遍歷破片包圍球和模型部件包圍球的碰撞檢測，由此可顯著提高程序的運行效率。

2.2 破片命中點參數的計算模型

2.2.1 Ray－3D射線的創建

通過包圍球碰撞檢測計算模型得到創建Ray射線的基本參數，即破片的運動方向和自上一幀以來運動的距離，用程序代碼表示為

Vector3direction＝currentPosition－lastPosition；

float distanceCovered＝direction.Length（）；

direction.Normalize（）； ／／ray方向歸一化

Ray ray＝new ray（lastPosition，direction）；

其中，direction為此時Ray射線的方向（即破片的包圍球與目標模型發生碰撞后破片的方向賦值給了Ray射線），這里進行單位化；currentPosition為Ray射線當前的位置坐標；lastPosition為Ray射線上一幀的位置坐標；distanceCovered為Ray射線運動方向和自上一幀以來運動的距離。獲得了Ray射線的一個點和它的方向，創建一條Ray射線，并且檢測Ray射線與模型部件包圍球的碰撞。

2.2.2 Ray－Triangle碰撞檢測模型

該計算模型分成2部分。首先找到射線與模型部件三角形面元的碰撞點。由于三角形面元和此相交點在同一個平面內，所以就轉換成了2D問題，如圖3所示。接下來要檢測碰撞點是否在三角形的內部。

圖3 3DRay－Triangle射線碰撞交點轉換為2D

運用2個方法處理圖3所示問題：①RayPlaneIntersection，給定一個Plane（目標模型某個三角形面元）和一條Ray射線相關參數，計算出射線與三角形面元之間的交點。②PointInsideTriangle，給定三角形面元的3個坐標和1個額外碰撞點參數，確定該碰撞點是否在三角形內部。如果在三角形面元內部就檢測到了射線和模型的碰撞。下面具體介紹以上2個方法的實現。

2.2.3 Ray射線與Plane之間的碰撞點模型

這里模型的計算方法采用了基于矢量的方法，如圖4所示。

由此時的Ray射線和1個三角形面元平面，可以得到ray.Direction和collisionPoint兩點間的距離，圖4中給出了該方法中的變量長度。

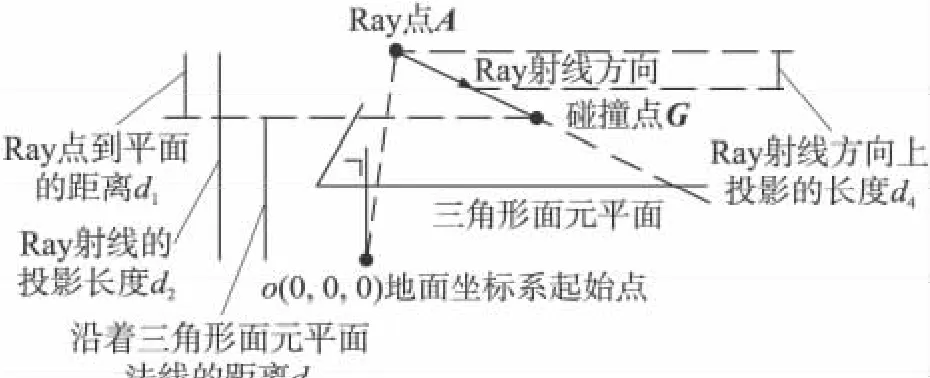
圖4 Ray射線上碰撞點的位置

通過Ray射線的投影長度d2（位于三角形平面法線上）和三角形面元平面法線的距離d3易求得Ray射線起始點到平面的距離d1：

設Ray射線在平面法線上投影長度為d4，通過式（6）由Ray射線投影長度與Ray射線起始點到碰撞點向量投影長度，可得Ray射線與碰撞點之間的比例因子k：

Ray射線的方向為RrayDir＝（RrayDirxRrayDiryRrayDirz）。

至此，由Ray射線的起始點A（之前破片包圍球與目標模型部件包圍球發生碰撞時破片的坐標）和式（7）可求得Ray射線與三角形面元碰撞點G的坐標：

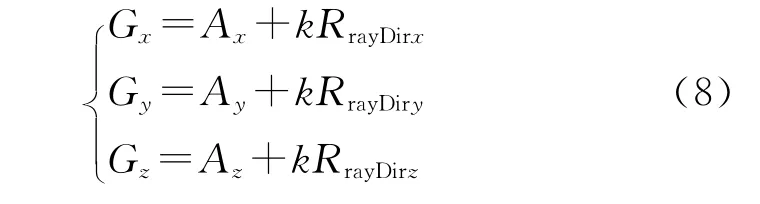
2.2.4 碰撞點是否在三角形內部的檢測模型

使用基于向量的方法檢測碰撞點是否在三角形內部，如圖5所示。

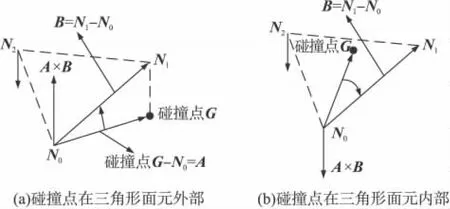
圖5 檢測碰撞點是否在三角形內部的示意圖

圖5 中，N0，N1，N2為某一個三角形面元的3個頂點，碰撞點為G，得到碰撞點G與N0的向量A＝（AxAyAz），則A的分量為

設向量B＝（BxByBz），為三角形面元頂點N0與N1之間的向量，則有

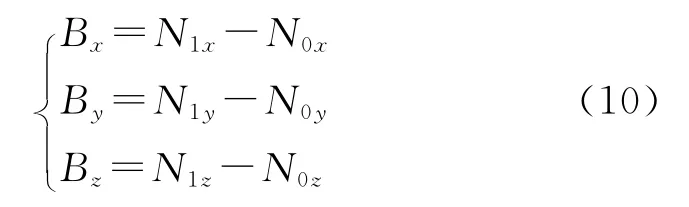
向量A和向量B的矢量積為向量n，用來判斷碰撞點在三角形邊界的哪一邊，則n的分量為

當逆時針旋轉向量A到向量B時，法向量指向三角形面元的上方，此時對應的碰撞點在三角形面元的外部，如圖5（a）；同理，若順時針旋轉向量A到向量B，法向量指向三角形面元的下方，此時對應的碰撞點在三角形面元的內部，如圖5（b）。當Ray射線與三角形面元平行時，碰撞點不存在，可跳出程序，進而循環遍歷與該部件其它三角形面元的交點。

2.2.5 射線與三角形面元的落角

通過上述計算模型求出射線與目標模型部件的三角形面元的交點，這里給出計算射線與三角形面元的落角的數學計算模型。由于一條射線和三角形面元的夾角并不能確定射線與三角形相交的唯一姿態，如圖6所示，這里通過計算射線與三角形面元的夾角α和射線與三角形面元所在軸（目標導彈的彈軸）的夾角β，可以唯一確定射線與三角形面元的姿態。

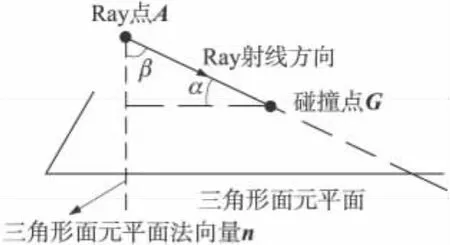
圖6 射線與三角形面元的夾角

由式（11）和Ray射線的方向可求得Ray射線與三角形面元法向量的夾角為

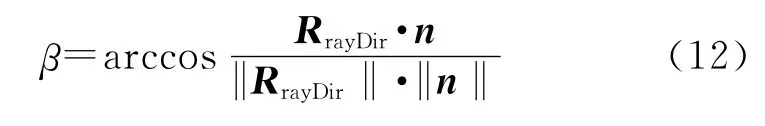
則Ray射線與三角形面元的夾角為

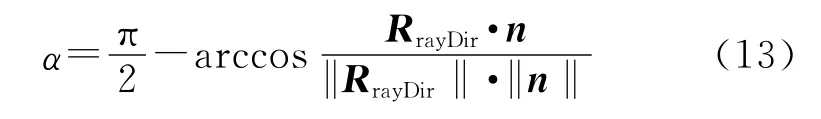
設此時目標模型的軸的方向向量為l＝（lxlylz），則Ray射線與軸的夾角為

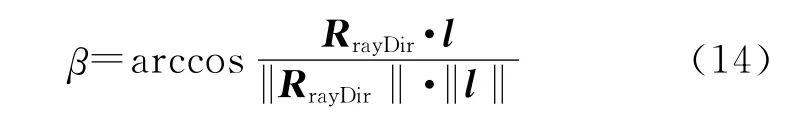
至此，即可求出Ray射線與目標面元的夾角和與目標軸線的夾角，Ray射線與三角形目標元的交點坐標及擊中速度，從而根據破片的質量求出擊中面元的動能等。

3 計算流程

求解破片命中目標的計算流程主要由包圍球的碰撞檢測流程和Ray射線命中目標計算流程組成，如圖7所示。

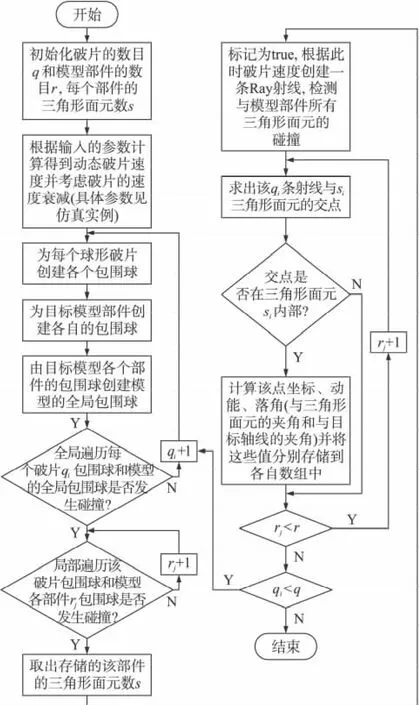
圖7 求解破片命中目標的計算流程圖

通過以上破片擊中目標的計算流程圖，實現了Ray射線局部遍歷目標模型部件三角形面元，這樣可以盡可能地增加目標上三角形面元的數目，使其保持在合理的范圍內，進而可以精確地得到命中點參數，提高了命中點參數的精度和程序的運行效率。

4 仿真實例

根據破片命中點計算數學模型，基于XNA以可視化的方式動態地顯示彈目遭遇、戰斗部起爆、破片動態飛散和破片的命中點坐標等。仿真程序采用Microsoft Visual Studio 2010語言編寫，使用XNA函數庫為圖形接口，精確計算并記錄破片命中點參數的數據。仿真軟件界面如圖8所示，由于篇幅有限，這里只顯示部分。

圖8（a）給出了初始化導彈和目標的姿態角參數，圖8（b）給出了目標質心在地面坐標系下的坐標，圖8（c）給出了導彈在地面坐標系下的坐標、導彈的靜態飛散角和飛散方向角、破片數、破片的質量，天線主瓣傾角和引信作用距離等，脫靶量和脫靶方位角隨機生成（計算中考慮了破片在不同高度時上述因素對破片速度衰減的影響），仿真實例生成的命中結果如圖9所示。

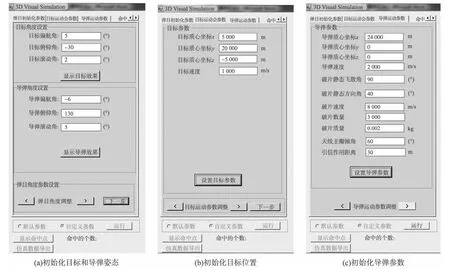
圖8 射線與三角形面元夾角的仿真計算

圖9 （a）生成了導彈戰斗部瞬間爆炸及其破片動態飛散的可視化效果，圖9（b）顯示了破片命中目標命中點分布情況，圖9（c）實時存儲了命中點的參數和落角（與目標模型三角形面元的夾角和與目標模型軸線的夾角）并最終以可視化的方式將上述命中點參數數據顯示出來。其中，命中目標的破片數為615，占破片總數的20.5%，存儲所得到的數據以便進一步分析和優化。

5 結論

本文提出了一種精確計算命中點參數的數學模型，可以有效地克服傳統計算方法的不足。該算法提高了計算精度和程序的執行效率，從而所得到的仿真結果更加真實可靠；更好地滿足了引戰配合可視化仿真的需要，效果理想；為地空和空空導彈引戰配合仿真軟件的研制提供了參考。

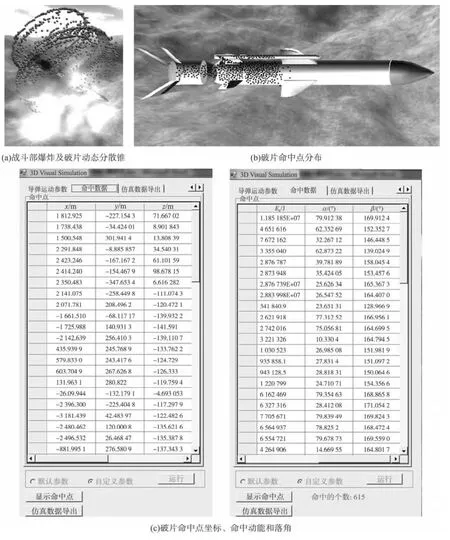
圖9 破片命中結果

［1］張志鴻，周春生.防空導彈引信與戰斗部配合效率和戰斗部設計［M］.北京：中國宇航出版社，1994：77－100.ZHANG Zhi－hong，ZHOU Chun－sheng.Air defense missile fuze and warhead designed with efficiency［M］.Beijing：China Astronautic Publishing House，1994：77－100.（in Chinese）

［2］李廷杰.導彈武器系統的效率及其分析［M］.北京：國防工業出版社，2000.LI Ting－jie.The effectiveness of missile weapon system and its analysis［M］.Beijing：National Defense Industry Press，2000.（in Chinese）

［3］BUSH J T.Visualization and animation of a missile／target encounter［D］.USA：Air Force Institute of Technology，USAF，1997.

［4］王宏波，莊志洪，張京國，等.引戰配合可視化仿真命中點參數精確計算［J］.系統仿真學報，2010，22（4）：1 071－1 074.WANG Hong－bo，ZHUANG Zhi－hong，ZHANG Jing－guo，et al.Accurate calculation of hitting point parameters in visual simulation of fuze－warhead coordination［J］.Journal of System Simulation，2010，22（4）：1 071－1 074.（in Chinese）

［5］王馬法，李翔宇，盧芳云，等.彈目交會中破片命中點參數計算模型研究［J］.彈道學報，2012，24（2）：50－54.WANG Ma－fa，LI Xiang－yu，LU Fang－yun，et al.A model of calculating hitting point parameters of fragment in waehead／target encounter［J］.Journal of Ballistics，2012，24（2）：50－54.（in Chinese）

［6］MILES R，MUSGRAVE D.Microsoft XNA game studio 4.0［M］.USA：A Division of Corporation One Microsoft Way，2011：300－500.

［7］MILLER T，JOHSON D.XNA game studio 4.0programming［M］.USA：U.S.Corporate and Government Sales，2011：400－482.

［8］耿肇英.Direct 3D與XNA游戲開發基礎［M］.北京：清華大學出版社，2008.GENG Zhao－ying.Direct and XNA game development foundation［M］.Beijing：Tsinghua University Press，2008.（in Chinese）

［9］AaronReed.學習XNA游戲編程［M］.北京：清華大學出版社，2011.AaronReed.Learning XNA game programming［M］.Beijng：Tsinghua University Press，2011.（in Chinese）

［10］劉彤.防空戰斗部殺傷威力評估方法研究［D］.南京：南京理工大學，2004.LIU Tong.Research on the lethality assessment method of anti－air warhead［D］.Nanjing：Nanjing University of Science and Technology，2004.（in Chinese）

［11］莊志洪，路建偉，張清泰，等.破片速度衰減對命中目標部位的影響［J］.彈道學報，1999.11（2）：5－8.ZHUANG Zhi－hong.LU Jian－wei，ZHANG Qing－tai，et al.Effects of fragments velocity fade on hitting point［J］.Journal of Ballistics，1999，11（2）：5－8.（in Chinese）

［12］盧永剛，錢立新，楊云斌，等.目標易損性／戰斗部威力評估方法［J］.彈道學報，2005，17（1）：46－52.LU Yong－gang，QIAN Li－xin，YANG Yun－bin，et al.Vulnerability／lethality assessment method based on virtual model［J］.Journal of Ballistics.2005，17（1）：46－52.（in Chinese）

［13］魏暄蓀，劉昌禮，黃長強.導彈／彈丸飛行力學［M］.西安：空軍工程學院，1996.WEI Xuan－sun，LIU Chang－li，HUANG Chang－qiang.Missile／projectile flight mechanics［M］.Xi’an：Air Force Engineering Institute，1996.（in Chinese）