結構地震響應控制的優化方法
代建波,王社良,趙 祥
(1.西安石油大學 機械工程學院,西安 710065;2.西安建筑科技大學 土木工程學院,西安 710055)
結構地震響應控制的優化方法
代建波1,王社良2,趙 祥2
(1.西安石油大學 機械工程學院,西安 710065;2.西安建筑科技大學 土木工程學院,西安 710055)
針對大跨空間結構地震響應主動控制,以超磁致伸縮材料為核心元件設計了一種可以應用于大跨空間結構振動主動控制中的超磁致伸縮作動器,制作出了作動器的原型并對其進行了輸出性能測試。使用遺傳算法對大跨空間結構主動控制作動器的布置位置進行了優化設計,最后進行了優化效果的數值模擬分析。以此驗證了超磁致伸縮作動器具有良好的作動效應,利用遺傳算法在大大提高結構主動控制優化設計效率時,可以保證實現對結構的整體優化以及作動器能高效、經濟地實現對結構進行主動控制的目的。
振動與波;大跨空間結構;地震響應;主動控制;超磁致伸縮作動器;遺傳算法
空間結構的跨度不斷增大,在外界動力荷載作用下,往往會發生大幅度的振動,以致會影響整個建筑的正常使用甚至造成破壞。結構振動控制可以有效地減少結構在風、地震等動力作用下的反應和損傷積累,有效地提高結構的抗震能力和抗災性能,是結構抗震減災積極有效的方法和技術[1]。被動、半主動控制技術在土木工程中得到了很好地、廣泛地研究及應用,而運用智能材料制作作動器進行結構地震響應主動控制具有靈活性、智能性、高效性等優點,可以更好的實現結構的振動控制。
超磁致伸縮材料GMM(Giant Magnetostrictive Material)是一種新型的智能材料,在磁場作用下,長度及體積均發生變化而對外做功,去掉外磁場后,又可以恢復原來的尺寸,因而能高效地實現電磁能與機械能之間的相互轉換,是重要的能量與信息轉換功能材料[2]。用GMM制作的作動器具有磁致伸縮應變量值大、能量轉換效率高、工作電壓低、響應速度快、承載能力強等無可比擬的優良特性,因而非常適宜用于大跨空間結構振動的主動控制[3]。
結構主動控制中一個重要的問題就是作動器位置的布置。雖然較多的作動器較易達到控制的目的,但會增加主動控制的實施難度和成本;因此,在作動器數目一定的條件下尋求最優布置位置以取得較高的控制效率對于主動控制就具有重要的意義。
1 GMM作動器的結構設計及性能試驗
1.1 GMM作動器總體結構設計
圖1為本文設計的GMM作動器的總體結構示意圖,圖2為GMM作動器實物圖。作動器包括外套、探測線圈、偏置線圈、激勵線圈、線圈骨架、GMM元件、作動桿、連接桿、預壓碟簧和調節螺母等,通電后偏置線圈、激勵線圈提供疊加磁場,單層探測線圈用于測量磁場的大小。GMM是低磁導率材料,為了盡大可能的提高其工作效率,設計了由GMM元件和高導磁外套筒構成的閉合磁路。因為外套筒的高導磁率,磁通幾乎全部被限制于外套筒中,磁力線沿著外套筒的路徑流通,均勻穿過GMM元件且于其伸長方向一致,從而降低了漏磁。在GMM元件伸長方向上用碟簧加一足夠大的反力,可起到預緊及增加位移輸出量的作用。為了可以控制施加的力的大小,在彈簧上部設計了調節螺母以調節碟簧預壓力的大小。當激勵線圈通以電流信號時產生磁場,GMM元件產生伸長變化且伸長效應通過作動桿輸出給作動對象,斷掉電流信號后磁場消失,GMM元件恢復原來形狀,完成此作動器的作動效應。

圖1 GMM作動器總體結構示意圖

圖2 GMM作動器實物圖
1.2 GMM作動器輸出性能
通過多功能力學試驗機對制作的GMM作動器進行了輸出性能測試,如圖3所示。圖4為不同預壓力作用下(0~20 MPa)作動器的輸出力隨電流強度(0~3.0A)變化的曲線圖。

圖3 GMM做動器輸出性能測試試驗
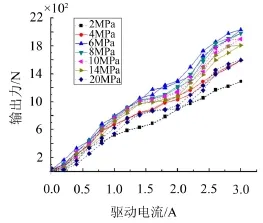
圖4 GMM作動器力輸出性能
由圖4可知,在一定驅動電流作用下,隨著預壓力的增大,作動器的輸出力開始增大,但是到6 MPa后,由于預壓力過大,輸出力開始緩慢下降。因此作動器預壓應力設計值定為6 MPa。而在6 MPa的預壓應力下,隨著驅動電流的增大,作動器的輸出力增大,在最大電流3A驅動下可以產生2 033 N的輸出力,且輸出力—驅動電流基本呈線性關系。
2 基于遺傳算法的GGMMMM作動器布置位置優化
結構主動控制中一個最重要的問題就是作動器位置的布置。在作動器數目一定的條件下如何找到使結構振動主動控制效果達到最優時的作動器的布置位置值得深入研究。
2.1 優化性能指標
作動器位置優化的關鍵就是找出一個評價大跨空間結構振動控制作動器布置位置優劣的性能指標。為了簡化推導,作出了以下假設:大跨空間結構中的桿件完全鉸接,結構振動完全處于彈性范圍內,不考慮作動器對大跨空間結構的質量、剛度矩陣的影響,結構的振動模態不會發生耦合現象。根據結構動力學可知,受控結構的動力方程可表示為[1]

其中M、C和K分別是質量、阻尼和剛度矩陣,X(t)分別為加速度、速度和位移向量。F(t)為外擾力向量,U(t)為控制力向量,Bs為作動器的位置矩陣,它由作動器的方向余弦組成,Ds為外擾力的位置矩陣。不考慮外擾力的作用,將式(1)轉換成模態方程。結構的第i個模態方程為

對向量Bi進行奇異值分解得

若模態qi可控,則矩陣Bi的奇異值矩陣可表示為:



利用新的模態坐標進行轉換得
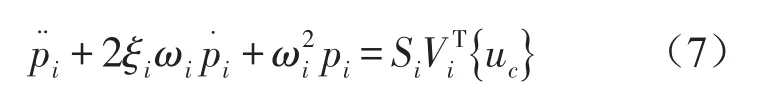


其中γi代表了結構中第i個受控模態的重要程度,因為結構振動的能量主要來自于地震,可以取γi為在地震影響系數曲線上ωi所對應的值。性能指標J的值越大,作動器的布置就越優越,即對結構的控制效果就越好。
2.2 適應度函數
利用2.1中所提出的性能指標進行優化,通過Matlab軟件建立優化模型。由于Matlab軟件中的GADS工具箱進行遺傳算法優化時,只能求得適應度函數的最小值,所以如要得出規定好的作動器的數目的優化位置,必須將上面求得的性能指標進行一些調整,從而得到適應度函數
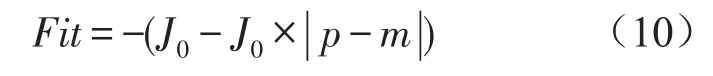
其中J0為調整前的適應度值,p為當前布置的作動器數目,m為預期布置的作動器數目。
2.3 數學模型
優化布置準則具有多樣性,對于建筑結構,基于安全性的要求,運用最大耗能原則和結構模態可控度的準則,求出的適應度值越小,代表結構的控制效果越好,作動器布置越優越。

2.4 遺傳算法優化步驟
針對大跨空間結構作動器優化布置問題,應用遺傳算法,采用以下步驟進行優化[6]。
(1)編碼與建立初始種群
針對本文研究對象,采用二進制碼對個體進行編碼,編碼長度為(r即大跨空間結構一共有r根桿件),假如第i個基因座的值為1,表示第i根桿上布置了作動器,若第i個基因座的值為0,表示該根桿上沒有布置作動器。設置初始種群為30個;
(2)適應度函數
適應度函數是用于對個體評價的標準,也是優化過程進行的依據,表明個體和解的優劣性。針對文中研究對象,利用提出的性能指標,即可進行適應度函數的編制,建立優化模型;
(3)選擇、交叉和變異操作
采用最佳保留選擇,以保證群體中的個體的適應度值不斷接近最優解,并設置交叉概率為0.8,變異概率為0.05,以增加種群的多樣性;
(4)算法終止條件
本文設置的算法終止條件為運算最大代數為200代,穩定代數為50代。整個遺傳算法優化流程如圖5所示。

圖5 遺傳算法優化流程圖
3 GMM作動器布置位置優化算例分析
3.1 計算模型
某大跨空間網架結構,如圖6所示,跨度40 m×40 m,高度4 m,倒放四角錐,桿件全部采用鉸接,所有桿件均采用Φ30×2的鋼管,結構的4個角點固結。此網架結構共有50個節點,160個桿件。應用遺傳算法,通過Matlab軟件進行編程,在放置10、20、30個作動器的條件下對此空間網架結構進行作動器布置位置優化計算。

圖6 大跨空間網架結構模型
3.2 優化結果
按照上述遺傳算法優化步驟對分別配置10、20、30個作動器時的大跨空間結構主動控制進行優化設計,優化參數選擇如表1所示。

表1 遺傳算法優化參數設置
表2給出了作動器優化結果,圖7—圖9分別為配置10、20、30個作動器時適應度曲線圖。

表2 不同數目作動器的優化后的布置位置

圖7
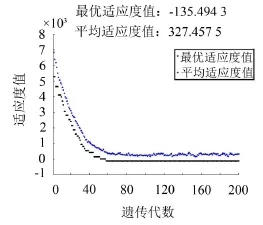
圖8
由圖7—圖9的適應度曲線圖可以看出每個適應度曲線中的適應度值隨著遺傳代數的增加都是不斷減小的,表明適應度值是處于逐漸收斂的狀態,相應的優化性能指標J不斷增大,在GMM作動器數量一定的情況下,J越大表明GMM作動器的布置位置越優越,從而證明了利用遺傳算法對空間網格結構中GMM作動器布置位置優化計算的可行性。從圖中還可以看出,隨著GMM作動器數量增多,適應度值逐漸減小,而且更快的趨向于最優解,說明隨著GMM作動器數量的增多,對結構的控制效果越來越好,而且可以更快的得出優化布置方案。從圖中還可以看出,配置30個作動器時,種群適應度在第25代收斂,目標函數計算不足800次,而采用窮舉法需要計算次,從而證明了利用遺傳算法對網架進行作動器位置優化的高效性。

圖9
圖10—圖12分別是布置10、20、30個作動器時,經過遺傳算法優化后作動器的布置位置圖。可以看出,作動器的位置集中在結構的四角和跨中,即在網架各階模態的節點附近,也就是結構各階振型變形最大的地方,具有明確的物理意義。由于結構形式完全對稱,作動器布置位置同時具有對稱性,并且隨著作動器數目的增多更加趨于均勻對稱。

圖10 10個作動器的優化布置圖

圖11 20個作動器的優化布置圖

圖12 30個作動器的優化布置圖
3.3 優化結果有效性分析
為了證明利用遺傳算法進行作動器布置位置優化的可行性和有效性,在布置30個作動器的情況下,采用LQR控制算法[7,8],對優化時采用的網架模型進行振動控制分析,分三種工況進行優化前和優化后的控制效果對比。在結構中輸入一條400 gal的X方向ELCENTRO波,故結構以水平振動為主,但大跨結構的豎向振動和位移不能忽略,故對跨中的23、25、26三個節點的X方向和Z方向進行控制效果的對比,并引入了2個控制效果系數,對比結果見表3,選取23節點兩個方向的位移時程曲線對比如圖13和圖14所示。

表3 三種工況下控制效果的對比

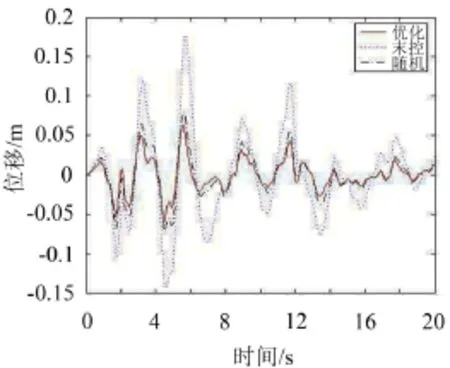
圖13 23節點X方向位移時程曲線對比圖

圖14 23節點Z方向位移時程曲線對比圖
由表3可知,采用30個作動器對模型結構進行主動控制,作動器位置采用隨機布置方式時,23節點X方向最大有55%的控制效果,Z方向最大有40%的控制效果。作動器位置采用優化布置方式時,23節點X方向最大有64%的控制效果,Z方向最大有57%的控制效果,比隨機控制時的控制效果分別增加了9%和17%。其它節點的控制效果也均有了較明顯的提高。證明了應用GMM作動器進行結構振動主動控制的可行性及應用遺傳算法進行對作動器布置位置優化的有效性。
4 結語
本文以GMM為核心元件設計制作了適合于土木工程結構的GMM作動器,并進行了性能測試。同時利用基于遺傳算法這一先進的優化方法對作動器進行了優化配置并進行了大跨空間網架結構控制效果的數值模擬分析,得到了以下結論:
(1)在充分研究了GMM磁控特性的基礎上,結合結構主動控制的特點設計了一種適合于土木工程結構的GMM作動器,并制作出了作動器的原型,并對GMM作動器進行了輸出性能測試試驗,分析了輸出力與驅動電流的關系;
(2)提出了在規定作動器數目的情況下評價平板網架結構振動主動控制作動器布置位置優劣的適應度函數;
(3)基于遺傳算法這一先進的優化方法,對平板網架結構主動控制中作動器的布置位置進行了優化設計,利用MATLAB編寫了適應度函數程序并應用GADS工具箱進行了優化計算,在提高優化設計計算效率的同時,保證了實現對結構的整體優化,避免陷入局部優化,達到高效、經濟的對結構進行主動控制的目的;
(4)應用MATLAB編寫了LQR控制算法程序對平板網架結構進行了主動控制的動力時程分析。通過結構在多種不同工況條件下控制效果的對比,驗證了應用遺傳算法對作動器布置位置優化的有效性和應用GMM作動器進行結構振動主動控制的可行性。
[1]歐進萍.結構振動控制—主動、半主動和智能控制[M].北京:科學出版社,2003.
[2]李梅,呂銀芳.超磁致伸縮材料及其應用[J].現代電子技術,2005,18:114-117.
[3]方紫劍,王傳禮.超磁致伸縮材料的應用現狀[J].煤礦機械,2006,27(5):725-726.
[4]張東昱.雙層柱面網殼主動控制及其優化研究[D].北京:北京工業大學,2001.
[5]周明,孫樹棟.遺傳算法原理及應用[M].北京:國防工業出版社,1999.
[6]雷英杰.MATLAB遺傳算法工具箱及應用[M].西安:西安電子科技大學出版社,2005.
[7]莫凡芒,孫慶鴻,陳南等.遺傳算法在結構振動主動控制中的應用研究[J].噪聲與振動控制,2003(2):11-12+16.
[8]王社良,紀慶波,代建波等.基于超磁致伸縮作動桿的結構振動主動控制研究[J].噪聲與振動控制,2010(6):23-26+42
Optimization Method for Structural Seismic Response Control
DAI Jian-bo1,WANG She-liang2,ZHAO Xiang2
(1.School of Mechanical Engineering,Xi’an Shiyou University,Xi’an 710065,China; 2.School of Civil Engineering,Xi’an University ofArchitecture and Technology,Xi’an 710055,China)
An actuator with giant magnetostrictive material(GMM)as the main components was designed for active vibration control of large-span spatial structures in earthquake situations.The prototype actuator was produced and the output performance was tested.The genetic algorithm was used to optimize the actuators layout in the large-span spatial structures.Numerical results of the optimization show that the GMM actuator has good vibration control efficiency.The genetic algorithm can greatly raise the effectiveness for the optimal design of the active control of the structures and guarantee the optimization of the overall structure. By optimizing the layout of the actuators,the active control of the structures can be realized effectively and economically.
vibration and wave;large-span spatial structure;seismic response;active control;GMM actuator;genetic algorithm
TB53;TU399
:A
:10.3969/j.issn.1006-1335.2015.01.009
1006-1355(2015)01-0042-06
2013-05-30
國家自然科學基金資助項目(51178388,51405385);西安石油大學青年科技創新基金項目(2013BS024);陜西省重點實驗室訪問學者項目(14JS045)
代建波(1983-),男,講師,博士,主要從事結構振動控制等方面的研究。
王社良(1957-),男,教授,博士生導師,主要從事結構振動控制、結構抗震等方面的研究。E-mail:wangshel@aliyun.com.

