復合材料層合板聲功率及靈敏度研究

吳錦武，薛曉理，彭文輝

（南昌航空大學 飛行器工程學院，南昌 330063）

復合材料層合板聲功率及靈敏度研究

吳錦武，薛曉理，彭文輝

（南昌航空大學 飛行器工程學院，南昌 330063）

采用分層理論結合有限元模型分析復合材料層合板結構的振動特性，并用聲輻射模態理論進行結構聲輻射分析。在此基礎上，分析聲功率關于設計參數的靈敏度，推導聲功率靈敏度的表達公式。以四層復合材料層合板為例，著重對聲功率關于層合板結構鋪層角度和鋪層厚度的靈敏度進行了分析研究。數值計算結果顯示在層合板基頻處，輻射聲功率達到最大值，同時在該處靈敏度有明顯的升降過程。另外，對于低噪聲層合板應以±45°對稱的鋪設將是最為恰當的設計方案。

聲學；聲輻射；聲功率靈敏度；層合板

研究結構聲功率及其靈敏度，是結構低噪聲設計重要內容之一。聲功率靈敏度是指聲功率關于設計參數的變化率，能夠量化各設計參數對聲功率的影響程度，以聲功率靈敏度為指標，可通過定量修改設計參數，降低結構輻射噪聲，是結構優化設計的重振動與聲優化設計而言，如基于經典層合板理論，結要途徑[1]。

近年來,對于一般振動板結構聲功率靈敏度的研究越來越多。例如姜哲等[1，2]對薄板結構和阻尼板結構的聲功率靈敏度進行了研究，杜向華等[3]分析了三類設計變量的聲功率靈敏度，對于層合板結構有限元方法研究層合板振動特征值對鋪設角度的靈敏度[4]以及層合板輻射聲功率優化設計[5，6]。由于層合板結構參數眾多，其對聲功率的貢獻不盡相同，即存在不同的聲功率靈敏度。因此，有必要對復合材料層合板結構的聲功率靈敏度進行分析。

本文主要基于分層理論結合有限元模型分析振動特性，通過聲輻射模態計算結構聲功率。著重就復合材料層合板的聲功率及其關于鋪設角度和鋪層厚度的靈敏度展開分析研究。

1 聲輻射模態模型

任意形狀的振動結構表面S以圓頻率ω振動，向無界空間V輻射聲。在空間V中充滿均勻介質，介質的密度為ρ，聲速為c。設振動表面S上的法向振速為U，輻射聲壓為P。對于單頻振動，結構的輻射聲功率可表示為[2,7]

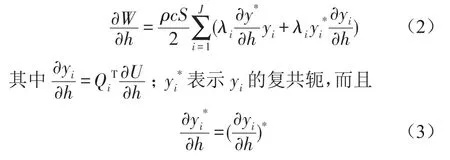
2 層合板動力學方程

通過分層理論，對每一層板在板厚方向采取二次插值，如圖1所示。

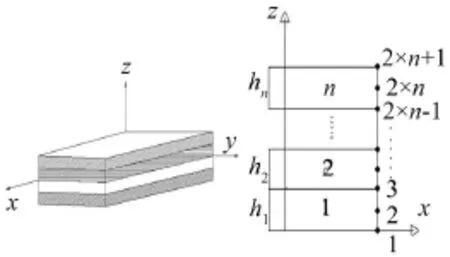
圖1 層合板的物理模型和坐標關系

層合板位移場可表達為[7]

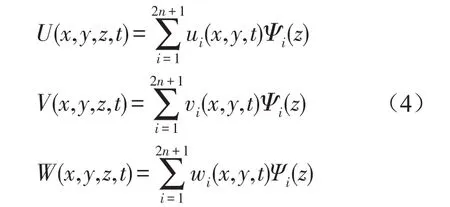
其中式（4）中U(x,y,z,t)，V(x,y,z,t)，W(x,y,z,t)分別為x,y,z方向位移，n為鋪設層數，2n+1為插值面數，ui(x,y,t)，vi(x,y,t)，wi(x,y,t)為第i個插值平面內x,y,z方向位移，Ψi(z)為插值展開系數，其值見參考文獻[7]。

根據有限元理論，式（6）中ui(x,y,t)，vi(x,y,t)，wi(x,y,t)表示為

式（5）中m為有限元單元節點數。Nk(x,y)為形函數表達式，uk,vk,wk為有限元節點k處的x,y,z坐標，T(t)為時間函數。根據有限元理論，本文采用四節點矩形單元，將式(5)和四節點形函數表達式代入式(4)，可得單元形函數矩陣N：

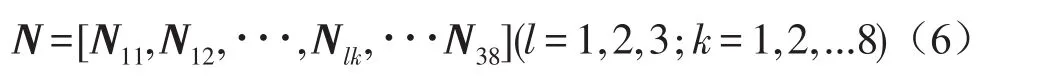
根據彈性力學位移－應變關系，可得到單元應變矩陣

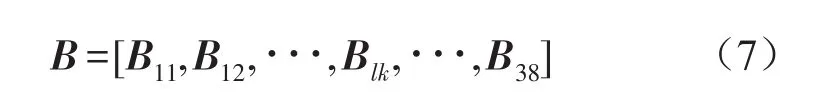
其中元素Bij見參考文獻[7]。

根據轉軸公式，當M坐標系與材料正軸坐標存在偏軸角，即層合板存在鋪設角度時，位移應變關系可表達為

其中式（8）中D為剛度矩陣，改變鋪設角度，剛度矩陣會發生改變。得到矩陣B和D后，單元剛度矩陣K和單元質量矩陣M以及阻尼矩陣C可以表示為

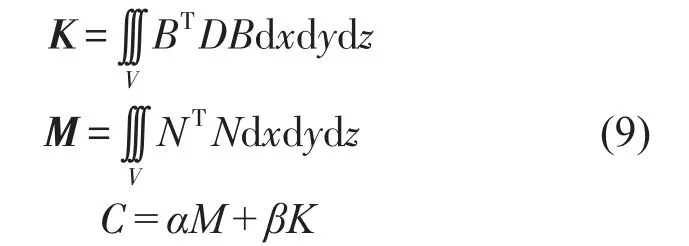
其中α，β分別為質量和剛度的比例系數。此時結構總動力方程為

其中X為振動法向位移向量。F0為激勵力幅值向量。層合板各階固有頻率可由行列式 |求得。

設在簡諧力激勵下結構法向位移響應形式為：X=X0eiωt，此時結構動力方程為

振動法向速度對設計參數h求偏導為

（11）兩邊對設計參數求偏導，結合式（12）可得

其中剛度矩陣K和質量矩陣M可直接對設計參數求偏導。已知振動速度對設計變量導數，可由式（2）得到聲功率靈敏度。

由式（9）和（13）可知：改變層合板纖維鋪設角度可改變層合板結構剛度；改變層合板結構厚度會影響結構質量。因此層合板結構纖維鋪設角度和層合板厚度的改變會影響層合板結構的聲功率。

3 算例及分析

3.1 不同鋪設角度聲功率及其靈敏度分析

四層四邊固支復合材料層合板長、寬、厚度分別為a=0.3 m，b=0.3 m，t=0.002 m。彈性模量分別為E1=124 Gpa，E2=E3=10.3 Gpa；剪切模量為G12=G23=G31=7.17 Gpa；泊松比μ=0.28，層合板鋪設角度取常見四種形式：[90°/0°]2，[±15°]2，[±30°]2，[±45°]2，在板中心施加單位激勵力F0，最大激勵頻率為1 000 Hz。此時不同鋪設角度下層合板結構固有頻率如表1所示。

表1 不同鋪設角度層合板前6階固有頻率

根據式（2）可得到不同鋪設角度四層固支層合板聲功率級與激勵頻率關系，所得結果如圖2。

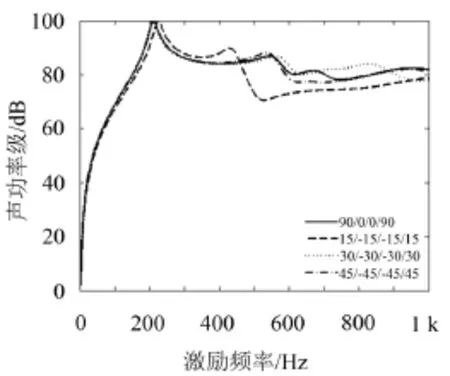
圖2 不同鋪設角度層合板輻射聲功率級

由圖2可知：在低頻時，不同鋪設角度時層合板結構聲功率相差不大，而且在基頻時聲功率達到最大；在高頻時，層合板以[±45°]2鋪設時聲功率較小，因此對于低噪聲層合板結構設計應盡可能以[±45°]2鋪設為佳。

從式(9)可知：改變鋪層角度可改變單元剛度矩陣。因此，聲功率關于鋪層角度的靈敏度可轉化成偏軸剛度矩陣對鋪層角度求導問題。通過計算得到層合板聲功率靈敏度與外激勵頻率的關系，所得結果如圖3。

由圖3可知：不同鋪設角度時，層合板結構在基頻處聲功率靈敏度有明顯的升降過程，因此在結構設計時應避免激勵頻率與基頻接近。另外在低頻時，[90°/0°]2鋪設時層合板結構聲功率靈敏度最大，在高頻時，不同鋪設角度下的聲功率靈敏度隨外界激勵頻率變化趨勢基本保持一致。

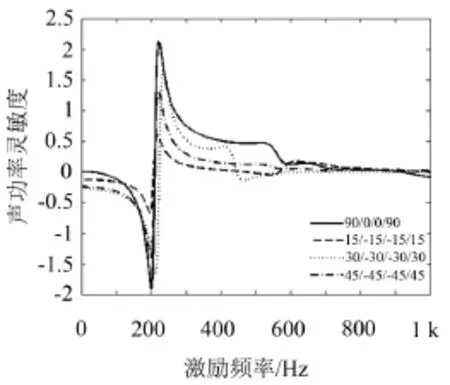
圖3 不同鋪設角度層合板聲功率靈敏度

3.2 不同鋪層厚度聲功率及其靈敏度分析

厚度影響層合板結構質量，從而影響層合板結構聲功率。在相同鋪設角度和層數的情況下，本文分兩種情況來討論結構聲功率及其靈敏度：

1）總鋪層厚度不同，每層皆為均勻分布；

2）總鋪層厚度相同，但每層厚度不同。

當總鋪層厚度不同，以四層厚度均勻分布的復合材料層合板為例，其材料性能參數同3.1所示，其中層合板鋪設角度為[45°/-45°]2，總鋪層厚度分別為h1=1.5 mm，h2=2 mm，h3=2.4 mm，h4=3 mm。計算四邊固支邊界條件下中點激勵層合板輻射聲功率及其靈敏度。

通過計算可得到總鋪層厚度不同下層合板結構的前六階固有頻率，結果如表2所示。由表2可知：隨著層合板結構厚度增加，對應的固有頻率值增大。根據式（4）可得到不同總鋪層厚度固支層合板聲功率級與外激勵頻率的關系，所得結果如圖4所示。

由圖4可知：不同總鋪層厚度的層合板都在基頻時聲功率達到最大，板厚為1.5 mm時聲功率峰值最大，2.4 mm時峰值最小，即隨著層合板結構厚度的增加，聲功率的峰值逐漸減小。在高頻時，不同總鋪層厚度的層合板結構聲功率變化不明顯。

從單元剛度矩陣K表達式(9)可知：鋪層厚度通過改變單元應變矩陣B來改變單元剛度矩陣。由參考文獻8可知：插值函數的取值與鋪層厚度直接相關。因此，聲功率關于鋪層厚度的靈敏度實際可以轉化成插值函數取值對鋪層厚度求導問題。通過計算得到不同總鋪層厚度層合板聲功率靈敏度與外激勵頻率的關系，所得結果如圖5。

由圖5可知：總鋪層厚度不同時，層合板結構在基頻處聲功率靈敏度有明顯的升降過程，因此在結構設計時應避免激勵頻率與基頻接近。另外在低頻時，鋪層厚度為1.5 mm時層合板結構聲功率靈敏度最大，2.4 mm時層合板結構聲功率靈敏度最小，在高頻時，不同總鋪層厚度下的層合板聲功率靈敏度隨外界激勵頻率變化趨勢基本保持一致。

表2 不同總鋪層厚度層合板前六階固有頻率

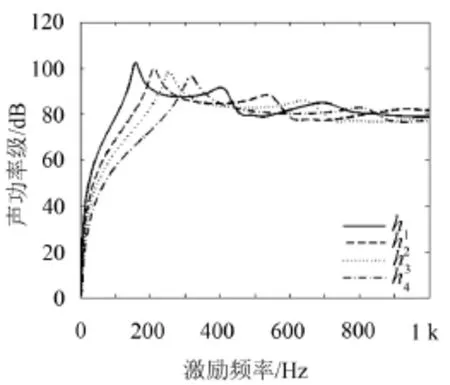
圖4 不同總鋪層厚度層合板輻射聲功率級

圖5 不同總鋪層厚度層合板聲功率靈敏度

當層合板總鋪層厚度相同，但每層厚度不同時，同樣以四層復合材料層合板為例，其材料性能參數見3.1節所示，層合板鋪設角度為[45°/-45°]2，板的總厚度都等于2 mm的情況下，各鋪層厚度采用等厚度和不等厚度兩種分布方式。等厚分布為[0.5/0.5/0.5/0.5]mm，不等厚分布取3種中心對稱分布情況分別為：[0.2/0.8/0.8/0.2]mm、[0.4/0.6/0.6/0.4]mm和[0.8/0.2/0.2/0.8]mm。

通過計算可得到單層鋪層厚度不同下層合板結構的前6階固有頻率，結果如表3所示。由表3可知：總厚度相同的情況下，不同單層鋪層厚度對層合板結構基頻影響不大。

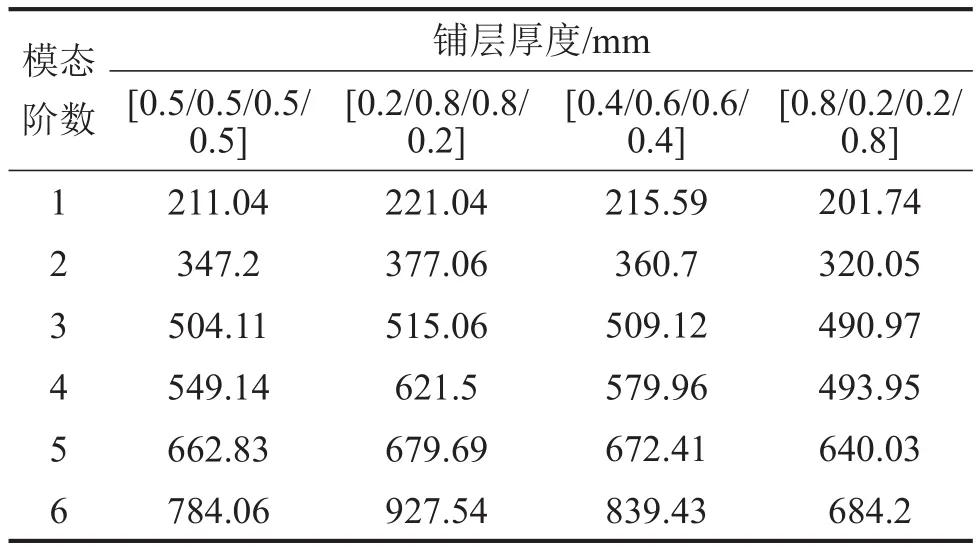
表3 不同單層鋪層厚度層合板前六階固有頻率

根據式（5）可得到不同單層鋪層厚度固支層合板聲功率級與外激勵頻率的關系，所得結果如圖6所示。由圖6可知：在低頻時，不同單層鋪層厚度時結構聲功率相差不大，而且在基頻時聲功率達到最大；在中頻時[0.8/0.2/0.2/0.8]mm鋪層的層合板聲功率最先出現衰減，[0.2/0.8/0.8/0.2]mm鋪層的層合板聲功率最后出現衰減，說明外面兩層鋪層厚度較大可以優先降低聲功率；在高頻時，不同單層鋪層厚度的層合板結構聲功率基本保持一致。

通過計算得到不同單層鋪層厚度層合板聲功率靈敏度與外激勵頻率的關系，所得結果如圖7。

由圖7可知：單層鋪層厚度不同時，層合板結構在基頻處聲功率靈敏度有明顯的升降過程，因此在結構設計時應避免激勵頻率與基頻接近。在高頻時，不同單層鋪層厚度的層合板結構聲功率靈敏度基本保持一致。

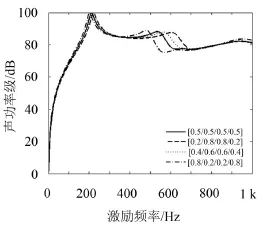
圖6 不同單層鋪層厚度層合板輻射聲功率級

4 結語

本文利用有限元與聲輻射模態對復合材料層合板結構的輻射聲功率及其關于設計參數的靈敏度進行了研究，重點推導了輻射聲功率對鋪設角度和鋪層厚度的靈敏度分析過程。以四邊固支層合板為例，數值計算結果表明：1）對于低噪聲層合板結構設計應盡可能以[45°/-45°]2鋪設為佳；2）在層合板基頻處，輻射聲功率達到最大值，同時在該處靈敏度有明顯的升降過程。即低噪聲設計時，應盡可能避免接近基頻附近。

Analysis of Sound Power and Sensitivity of Composite Laminate Plates

WU Jin-wu,XUE Xiao-li,PENG WEN-hui
(School ofAircraft Engineering,Nanchang HangKong University,Nanchang 330063,China)

The vibration characteristic of a composite laminate plate was studied by using FEM and laminate plate theory,and the sound radiation mode method was used to analyze the structural sound radiation of the plate.Then,the sound radiation sensitivity to design parameters was analyzed by using the sound radiation power and its expression was formulated.A four-layer composite plate was used as an example,and the sound power sensitivities to the ply angles and thickness of the plate were investigated.The numerical simulations show that the 45°symmetric ply angle is the best for the laminate plate, and the noise of the plate can be reduced significantly.In addition,the acoustic power reaches the maximum at the fundamental frequency of the laminate plate.Meanwhile,the acoustic power sensitivity has a peak value also at this frequency.

acoustic;sound radiation;sound power sensitivity;laminate plate

TB132

：A

10.3969/j.issn.1006-1335.2015.01.024

1006-1355(2015)01-0119-04+126

2014－06－25

國家自然科學基金項目(51265038)

吳錦武(1976－)，男，博士，碩士生導師，主要研究方向：振動與聲研究。E-mail:jinwu.w@hotmail.com