基于模糊FMEA的環己酮肟重排反應器風險分析

郭 凡 於孝春 袁東明

(南京工業大學機械與動力工程學院)

基于模糊FMEA的環己酮肟重排反應器風險分析

郭 凡*於孝春 袁東明

(南京工業大學機械與動力工程學院)

生產己內酰胺最重要的工藝過程就是環己酮肟液相貝克曼重排反應過程，其中連續三級重排反應器是主要設備之一。針對工藝環境對設備的影響，采用故障模式與影響分析(FMEA)方法對反應器進行失效分析，但是傳統的FMEA主觀性太大，精確度低。根據專家調查表，引入模糊綜合評判方法進行建模分析，采用層次分析法(AHP)確定權重向量和風險等級。模糊綜合評價對FMEA進行定量轉化，使重排反應器的風險評估更加合理。

重排反應器 環己酮肟 故障模式與影響分析 模糊綜合評判 風險分析

近年來全世界的己內酰胺需求量急速上升，我國也相繼建立多家廠房，己內酰胺生產工藝龐大、設備復雜、易燃易爆物料繁多。己內酰胺(CPL)作為重要的化工原料之一，主要用于生產工程塑料與聚酰胺纖維。當前90%左右的廠家采用發煙硫酸或濃硫酸作為催化劑，在三級重排反應器中進行貝克曼重排反應，使環己酮肟發生重排反應生成粗己內酰胺，再進一步精制出產CPL。由于在高溫環境下，伴隨大量酸性物質的存在，對環境污染大、副產品諸多及設備腐蝕嚴重等問題需要及時進行安全分析，確定風險等級，采取相應檢修措施[1]。

1 重排反應器故障模式及影響分析

傳統的FMEA風險分析屬于半定量分析法，通過經驗總結設備發生的故障模式、原因和影響，給予專家主觀的事故嚴重度(S)、故障發生頻度(O)和檢測難度(D)，并按照3個因素相乘得到風險順序數(RPN)[2，3]。依靠專家經驗知識打分，帶有嚴重的主觀性和模糊性，所以結合模糊綜合評價方法更具有準確性。根據環己酮肟重排工藝分析出可能發生的故障模式有：腐蝕、磨損及堵塞等，由于主要介紹多級模糊FMEA評價方法，應用到每個故障模式都是一樣的分析過程，加上篇幅的限制這里只介紹腐蝕失效的模糊評價過程，具體的重排反應器FMEA見表1。

2 模糊FMEA綜合評價

在重排反應器FMEA分析的基礎上加入模糊綜合評價，根據10位專家調查所得數據建立相應模糊矩陣，在確定權重時采用層次分析法(AHP)，從而將嚴重度、故障發生頻度和檢測難度3個因素對風險的影響進行加權分析，建立FMEA風險模型，把定性分析轉化為定量分析[4，5]。最后進行去模糊化(清晰化)分析，得到準確的風險等級。

表1 重排反應器FMEA

2.1確定因素集合

對照表1，環己酮肟重排反應器的腐蝕失效(二級指標)為研究對象，選取嚴重度、故障發生頻度和檢測難度3個因素為確定因素，則因素集U={嚴重度U1，發生頻度U2，檢測度U3}；每個因素Ui(i=1，2，3)(一級指標)由基本因素ui所決定，則Ui的因素集為Ui={應力腐蝕開裂u1，殘余應力u2，熱處理不當u3，選材不當u4，飛溫u5}。

2.2確定評語集

每個因素Ui(i=1，2，3)可以用5個等級表示，對U1的模糊語言為“非常嚴重、較嚴重、一般、輕微、幾乎無影響”；對U2的等級模糊語言為“經常發生、有時發生、偶爾發生、很少發生、極少發生”；對U3的等級為“無法檢測、檢測較低、中等、檢測較高、非常高”。依據以上5個等級，因素Ui(i=1，2，3)的評語集V依次為：V1={v11，v12，v13，v14，v15}；V2={v21，v22，v23，v24，v25}；V3={v31，v32，v33，v34，v35}。

2.3模糊評判矩陣

對于模糊評價矩陣的建立需要有專家的評論，論文根據以往記錄的10位專家(n=10)調查表2，分別統計出每個因素Ui(i=1，2，3，4，5)中專家評論的次數。

表2 專家對各因素評語(v1i，v2i ，v3i)調查表

根據表2可以統計出各因素Ui(i=1，2，3，4，5)中各種評語出現的次數記錄為nj，對u1的評語v1i(i=1，2，3，4，5)出現的次數依次為：n1=4，n2=2，n3=2，n4=1，n5=1；v2i(i=1，2，3，4，5)出現的次數依次為：n1=2，n2=2，n3=3，n4=2，n5=1；v3i(i=1，2，3，4，5)出現的次數依次為：n1=1，n2=2，n3=3，n4=3，n5=1。對u2的評語v1i(i=1，2，3，4，5)出現的次數依次為：n1=3，n2=4，n3=1，n4=1，n5=1；v2i(i=1，2，3，4，5)出現的次數依次為：n1=1，n2=4，n3=3，n4=1，n5=1；v3i(i=1，2，3，4，5)出現的次數依次為：n1=1，n2=5，n3=2，n4=1，n5=1。對u3的評語v1i(i=1，2，3，4，5)出現的次數依次為：n1=2，n2=1，n3=4，n4=2，n5=1；v2i(i=1，2，3，4，5)出現的次數依次為：n1=1，n2=2，n3=4，n4=2，n5=1；v3i(i=1，2，3，4，5)出現的次數依次為：n1=1，n2=3，n3=2，n4=2，n5=2。對u4的評語v1i(i=1，2，3，4，5)出現的次數依次為：n1=2，n2=3，n3=2，n4=2，n5=1；v2i(i=1，2，3，4，5)出現的次數依次為：n1=0，n2=2，n3=2，n4=3，n5=3；v3i(i=1，2，3，4，5)出現的次數依次為：n1=0，n2=3，n3=1，n4=3，n5=3。對u5的評語v1i(i=1，2，3，4，5)出現的次數依次為：n1=3，n2=3，n3=2，n4=2，n5=0；v2i(i=1，2，3，4，5)出現的次數依次為：n1=2，n2=4，n3=2，n4=2，n5=0；v3i(i=1，2，3，4，5)出現的次數依次為：n1=2，n2=4，n3=2，n4=1，n5=1。

根據公式Pj=nj/n，可以求得評語集V1對各因素ui(i=1,2,3,4,5)的評判向量依次為：

r1={0.4,0.2,0.2,0.1,0.1}

r2={0.3,0.4,0.1,0.1,0.1}

r3={0.2,0.1,0.4,0.2,0.1}

r4={0.2,0.3,0.2,0.2,0.1}

r5={0.3,0.3,0.2,0.2,0}

根據公式Pj=nj/n，可以求得評語集V2對各因素ui(i=1,2,3,4,5)的評判向量依次為：

r1={0.2,0.2,0.3,0.2,0.1}

r2={0.1,0.4,0.3,0.1,0.1}

r3={0.1,0.2,0.4,0.2,0.1}

r4={0,0.2,0.2,0.3,0.3}

r5={0.2,0.4,0.2,0.2,0}

根據公式Pj=nj/n，可以求得評語集V3對各因素ui(i=1,2,3,4,5)的評判向量依次為：

r1={0.1,0.2,0.3,0.3,0.1}

r2={0.1,0.5,0.2,0.1,0.1}

r3={0.1,0.3,0.2,0.2,0.2}

r4={0,0.3,0.1,0.3,0.3}

r5={0.2,0.4,0.2,0.1,0.1}

由此構成的Vi對Ui的模糊評判矩陣依次為R1,R2,R3：

2.4確定每個因素權重

在建立權重時，筆者采用層次分析法(AHP)[6]，建立矩陣時以第一層的要素FH為評判準則，對第二層的因素A1,A2，…，An進行兩兩相互比較來確定矩陣的元素值，建立層次之后也就得到了第一、二層之間的隸屬關系[7]。筆者采用簡捷的三標度法[8]，三標度使得專家對各個要素的重要度比較容易做出判斷，不會出現邏輯錯誤。具體尺度見表3，然后對專家調查表建立一級指標的相對重要度(表4)。

表3 三標度矩陣

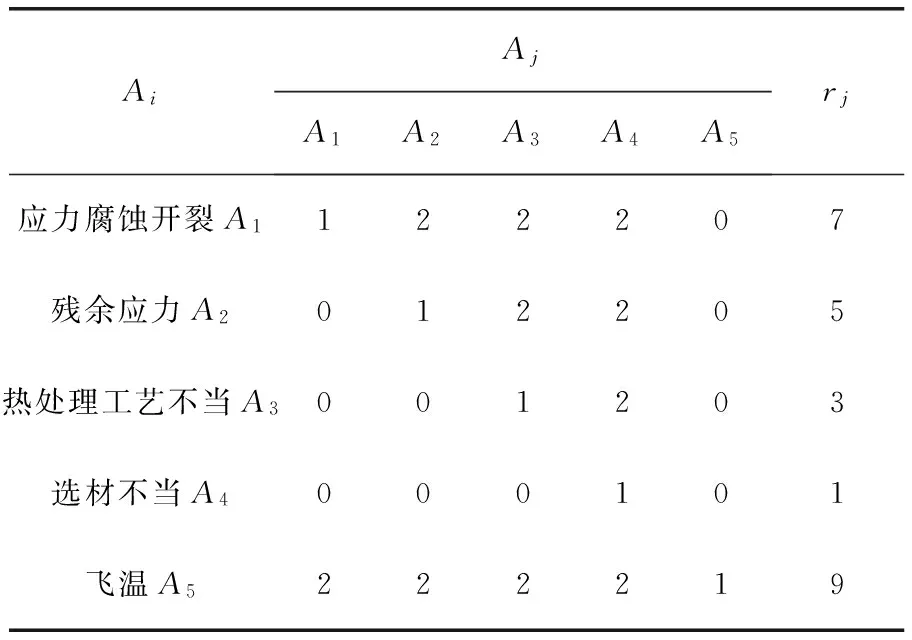
表4 反應器腐蝕失效各因素三標度矩陣表

由表4可以看出rmax=9，rmin=1，將三標度轉化為九標度時根據bm=9，可以計算得到各因素的權向量與最大特征值，分別見表5、6。

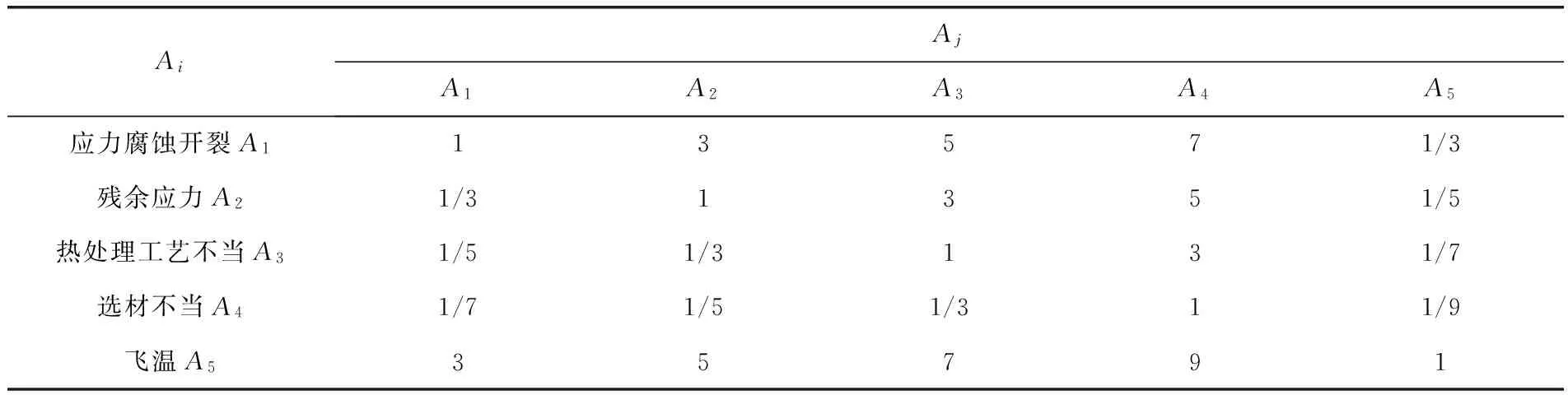
表5 反應器腐蝕失效各因素九標度矩陣表

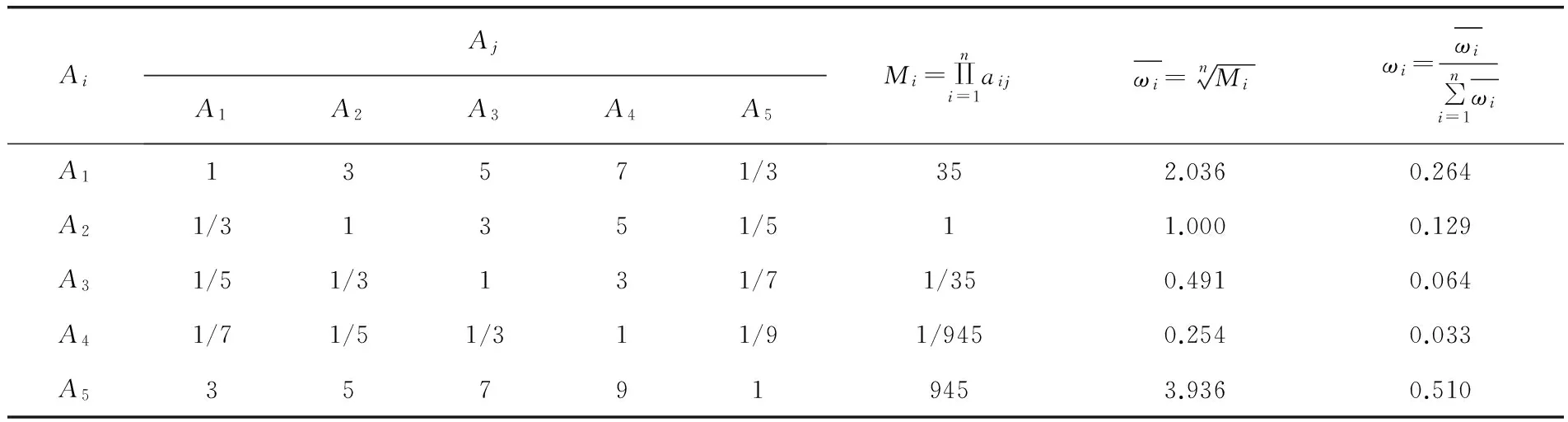
表6 各因素的權向量與最大特征值

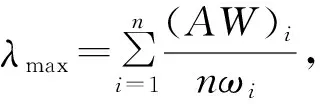
2.5一級模糊評判

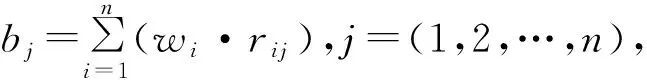
B1=W1×R1T

=(0.3167 0.2737 0.1999 0.1607 0.0490)

B2=W2×R2T

=(0.1741 0.3278 0.2521 0.1904 0.0556)

B3=W3×R3T

=(0.1477 0.3504 0.2231 0.1658 0.1130)

進行歸一化計算可得：

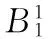
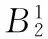
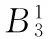
由一級模糊評判的結果可以看出對于FMEA中事故嚴重度因素來說，幾乎只有4%的專家認為開裂不會發生重大事故，普遍認為其具有一定的危害性。分別約有30%左右的專家認為腐蝕會造成非常嚴重事故或者較重大事故，20%的專家認為發生事故的嚴重度一般，16%認為發生事故嚴重程度比較低。基于最大隸屬度的原則，以31%的嚴重程度認為腐蝕失效造成嚴重的危害。對照傳統FMEA的嚴重度劃分表[8]是設備發生嚴重故障，操作起來有困難。

對于故障發生頻率因素來說，幾乎所有專家認為會發生故障，約33%的專家認為發生的頻率比較高，17%的專家認為發生腐蝕不可避免，約25%認為發生頻率只是偶爾發生，根據最大隸屬度原則選擇最高值，以33%的幾率認為反應器腐蝕的故障模式經常發生，對照傳統FMEA發生頻度等級劃分表其發生頻率為約1/3。

對于可探測度來說，35%的專家認為腐蝕失效檢測難度大，23%專家認為檢測難度一般，約有11%的專家認為檢測很容易。根據最大隸屬度原則，認為35%的幾率腐蝕失效一般比較難檢測出來，對照傳統FMEA檢測難易度等級表可以看出采用一定的措施才可以探測出問題所在。

2.6二級模糊綜合評判

由上面可得到的一級評判結果可以得到二級評價矩陣：

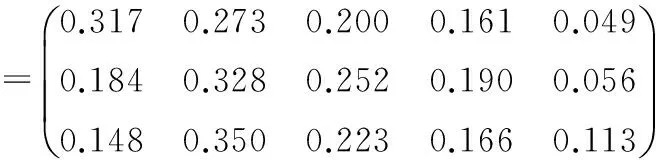
設對U1、U2、U3的權重分配為：W=(0.4,0.3,0.3)，從而可以得到反應器發生腐蝕失效的二級評判結果為：B2=W×R=(0.2264,0.3126,0.2225,0.1712,0.0703)。

2.7模糊向量明確化

由于上述結果為模糊向量，需要加以明確其評判等級，將模糊向量解模糊即清晰化，一般有最大隸屬度和重心法[9，10]。最大隸屬度就是對評判向量b利用最大隸屬度法b0=max(b1，b2，…，bn)，得到評判結果b0。方法簡單明了但是精確度不夠，考慮的影響因素也比較少。

重心法也就是加權平均法能夠考慮全面的二因素，該方法類似于求數學期望過程，加權系數μ(ui)、[μ(ui)]2(增加隸屬度較大元素)不同得到精確值也不相同。計算公式為：

對于反應器模糊評價選用重心法來進行清晰化處理，加權系數采用[μ(ui)]2，由于評語集Vi(i=1,2,3)是不同的，需要重新定義并對評語集的等級賦予數值(表7)。

重新定義的評語集，可以得到清晰化處理公式為：

表7 新定義評語集表

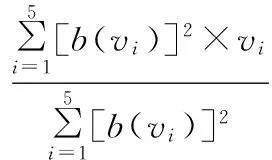
B0為評判的反應器的安全等級，取值為1～5之間：

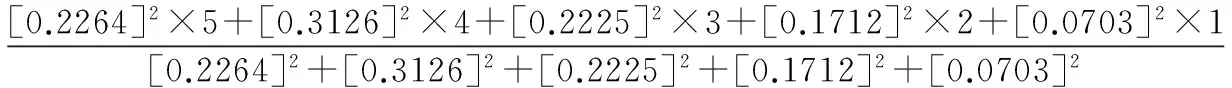
3 結論

3.1對于重排反應器發生腐蝕的失效原因經過FMEA危險排序法得到結果多數為高風險值，發生的嚴重度、頻度及檢測度都有很大的不確定性和模糊性。基于模糊綜合評判的FMEA分析，從定量方法上嚴格證明了方法的準確性。

3.2從計算結果B0=3.492可以看出等級在3～4之間，可見反應器安全性處于接近較差，相比于反應器的FMEA表1中所示的RPN順序表普遍都是高風險，模糊評價使得風險等級降低一個等級屬于偏于中等風險，采用模糊綜合評價使得結果更具精確，確定反應器為中高風險，需要制定合理的檢測與維護規程，對設備加強監測，避免操作中帶來過多殘余應力，正確選擇耐腐蝕材料，也要做好如噴涂等防腐措施，一旦發生異常及時采取措施制止，以防發生火災爆炸等嚴重事故。

[1] 陳德芳.己內酰胺生產中環己酮肟重排過程的探討[J].合成纖維工業，1992，15(4)：44～49.

[2] 陳新飚. FMECA技術在船舶防腐防漏中的應用研究[J].中國質量，2010，(7)：39～43.

[3] 胡燈明，鄭志強.油氣管道安全預評價的FMEA方法分析[J].石油化工安全環保技術，2010，26(4)：21～26.

[4] Cui X，Liu H J，Ying L M，et al.Multi-level Fuzzy Comprehensive Evaluation of Power Supply Serviee Quality[C]. Power System Technology.Chongqing：IEEE，2006：l～6.

[5] Wang L，Zeng Y R，Zhang D F.A New Approach to Evaluating the Critieality Class of SPare Parts Ineorporating Fuzzy Comprehensive Evaluation and Grey Relational Analysis[C].Computational Intelligence and Security.Guangzhou：IEEE，2006：17～21.

[6] 趙煥臣，許樹柏，和金生.層次分析法[M].北京：科學出版社，1986.

[7] 黃俊，付湘，柯志波.層次分析法在城市防洪工程方案選擇中的應用[J].水利與建筑工程學報，2007，5(1): 52～55.

[8] 王紹印.故障模式和影響分析(FMEA)[M].廣州：中山大學出版社，2003.

[9] 蘇欣，袁宗明，王維，等.層次分析法在油庫安全評價中的應用[J].天然氣與石油，2006，24(1)：1～4.

[10] 宋維華，殷位洋.淺談層次分析法在預防地鐵火災事故中的應用[J].現代城市軌道交通，2007，(1)：45～47.

RiskAnalysisofCyclohexanoneOximeRearrangementReactorsBasedonFuzzyFMEA

GUO Fan, YU Xiao-chun, YUAN Dong-ming

(SchoolofMechanicalandPowerEngineering,NanjingUniversityofTechnology,Nanjing211816,China)

Three-stage consecutive rearrangement reactor is the main device for cyclohexanone oxime’s Beckmann rearrangement reaction. Aiming at the environmental influence on the equipment, the method of failure mode and effect analysis (FMEA) was applied to the reactor failure analysis, but its low accuracy exists. The fuzzy comprehensive evaluation method was introduced to the modeling analysis, including the analytic hierarchy process (AHP) to determine both weight vector and risk level. The results show that this fuzzy FMEA quantitative analysis method can make the safety assessment of the rearrangement reactor more reasonable.

rearrangement reactor, cyclohexanone oxime, FMEA, fuzzy comprehensive evaluation, risk analysis

*郭 凡，女，1988年2月生，碩士研究生。江蘇省南京市，211816。

TQ052.5

A

0254-6094(2015)01-0006-06

2014-03-24)