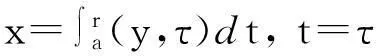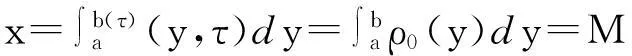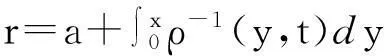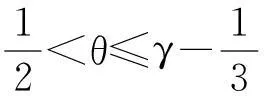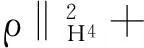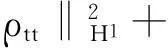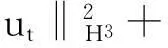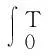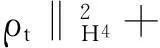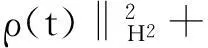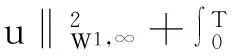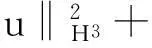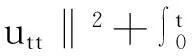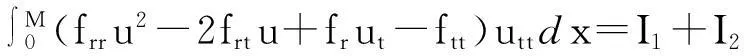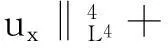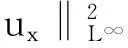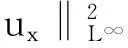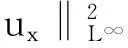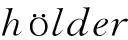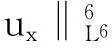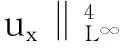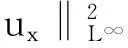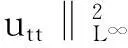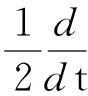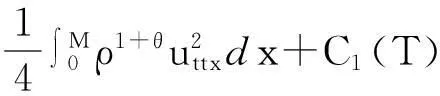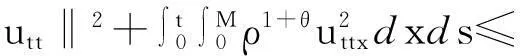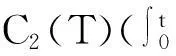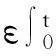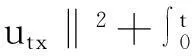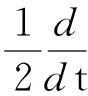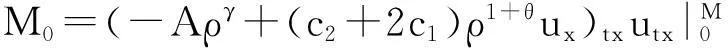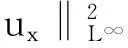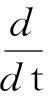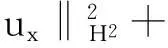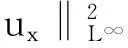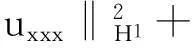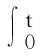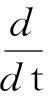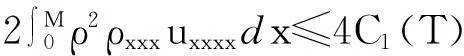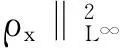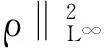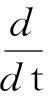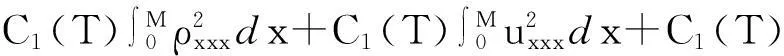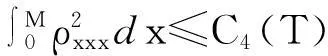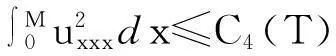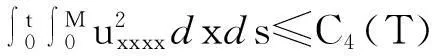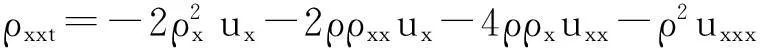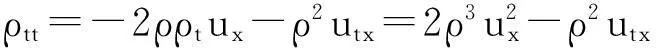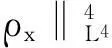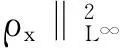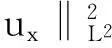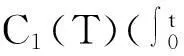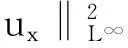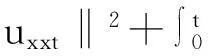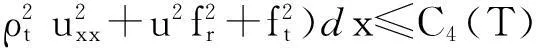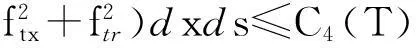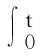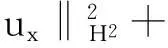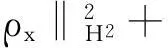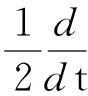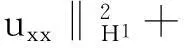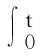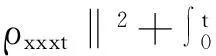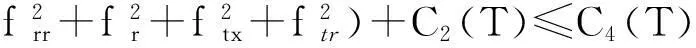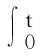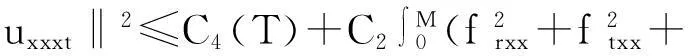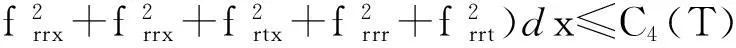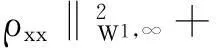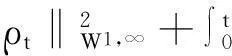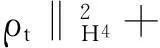帶有外力項和真空的可壓縮的Navier-Stokes方程的解在H4空間中的整體存在性

·數理科學·

帶有外力項和真空的可壓縮的Navier-Stokes方程的解在H4空間中的整體存在性

孔春香

(延安大學 數學與計算機科學學院, 陜西 延安716000)

摘要：在壓力和黏性系數是密度的一般函數的情況下,研究了可壓縮的Navier-Stokes方程整體解的存在性問題,為了克服外力和黏性系數依賴密度給研究所帶來的困難,得到了一些新的先驗估計。

關鍵詞：Navier-Stokes 方程;黏性依賴密度;外力項;整體存在性

收稿日期：2014-04-11

基金項目：陜西省高水平大學建設專項基金資助項目(2012SXTS07),陜西省自然科學基礎研究計劃基金資助項目(2012JM1012)

作者簡介：孔春香，女，河南蘭考人，從事偏微分方程研究。

中圖分類號：O175.26

Global existence behavior of the solutions in spaceH4for compressible

Navier-Stokes equations with external force and vacuum

KONG Chun-xiang

(College of Mathematics and Computer Science, Yan′an University, Yan′an 716000，China)

Abstract:This paper discusses the global existence of solutions to compressible Navier-Stokes equations with density-dependent the pressure and viscosity coefficient, in order to overcome density-dependent the pressure and viscosity coefficient, some new priori estimates are derived.

Key words: Navier-Stokes equation; density-dependent viscosity; external force; global existence

在歐拉坐標下,我們考慮帶有外力項和真空的可壓縮等熵的Navier-Stokes方程

?tρ+?r(ρu)=0,τ>0，

(1)

ρ(?tu+u?ru)+?rP=

?r[(λ+2μ)?ru]-ρf,a

(2)

其中ρ=ρ(r,τ),u=u(r,τ),P(ρ),f(m(ρ,r),r,τ)分別表示密度、速度、壓力、外力。λ(ρ)和μ(ρ)表示黏性系數。

初始條件:

(ρu)(r,0)=(ρ0,u0)(r),

a≤r≤b(0)=b。

(3)

邊界條件:

u|r=a=0,ρ|r=b(τ)=0。

(4)

這里b′(τ)=u(b(τ),τ),τ>0。考慮最著名的多方氣體模型P(ρ)=Aργ,γ>0和A>0是常數。假設μ(ρ)=c1ρθ,λ(ρ)=c2ρθ,c1,c2,0<θ<1都是正常數。

為了方便得到解的一些估計，把上述方程轉換成拉格朗日坐標下的方程。引入下面的坐標變換

(5)

ρt+ρ2ux=0,

(6)

ut+P(ρ)x=[(λ+2μ)ρux]x-f(x,r,t)，

(7)

(8)

初始條件:

(ρ,u)(x,0)=(ρ0,u0)(x),

(9)

邊界條件：

u|x=0=0,ρ|x=M=0,t>0。

(10)

本文中‖·‖表示L2范數,Ci表示與初值,時間T有關的常數。

1主要結果

假設初值滿足

(A1)γ>1+θ,0

(A2)ρ0∈Hi[0,M],u0∈Hi[0,M](i=2,4)。

外力f滿足

(A3)fr∈C2(0,T;H2[0,M]),

frr∈C1(0,T;H1[0,M]),

ft∈C2(0,T;H2[0,M]),

frr∈L2(0,T;L2[0,M]),

frrr∈L2(0,T;L2(0,M))。

定理1在(A1)～(A3)的條件下,在H4空間中問題(6)～(10)存在唯一的整體解(ρ(x,t),u(x,t)), 使得對任意T>0下列關系式成立

2先驗估計

引理1[11]

0

?(x,t)∈[0,M]×[0,T]，

(11)

(12)

引理2

‖utx(x,0)‖+‖utxx(x,0)‖+

‖utt(x,0)‖≤C4(T)，

(13)

(14)

證 明由式(7)和引理1得

‖ut‖≤C1(T)(‖ux‖H1+‖ρx‖+‖f‖)，

(15)

式(7)關于x求導,并由引理1得

‖utx‖≤C1(T)(‖ux‖H2+

‖ρx‖H1+‖fx‖+‖fr‖)，

(16)

或

‖uxxx‖≤C1(T)(‖utx‖+‖ux‖H1+

‖ρx‖H1+‖fx‖+‖fr‖)。

(17)

式(7)關于x求兩次導數,并由引理1及嵌入定理得

‖utxx‖≤C1(T)(‖ux‖H3+‖ρx‖H2+

‖fxx‖+‖frx‖+‖frr‖)，

(18)

或

‖uxxxx‖≤C1(T)(‖utxx‖+‖ux‖H2+

‖ρx‖H2+‖f‖H2+‖fr‖H1+‖frr‖)，

(19)

式(7)關于t求導,并由引理1和式(6)及嵌入定理得

‖utt‖≤C1(T)(‖ux‖H1+

‖ρx‖+‖utx‖+‖utxx‖+

‖ft‖+‖fr‖)。

(20)

把式(16)和式(18)代入式(20)得

‖utt‖≤C1(T)(‖ux‖H3+‖ρx‖H2+

‖f‖H2+‖fr‖H1+‖ft‖+‖fr‖+

‖frr‖)。

(21)

聯立式(16),(18)和(21)和條件(A3)得(13)。

式(7)關于t求兩次導,其結果乘以utt在[0,M]上積分并分部積分,利用式(6)和邊界條件(10)、引理1得

(22)

下面估計I1和I2。

由引理1和h?lder不等式及插值不等式得

C1(T)(‖utx‖2+‖ux‖2+‖uxx‖2)。

(23)

ε‖utt‖2+C1(T)(‖ux‖2+

‖uttx‖2+‖utx‖2)+C1(T)。

(24)

把式(23)和(24)代入(22)得

C1(T)(‖utx‖2+‖ux‖2+‖uxx‖2)+

ε‖utt‖2+C1(T)(‖ux‖2+‖utx‖2)+

上式兩邊在[0,t]上積分,并利用式(13),引理1得

引理3

(25)

證 明式(7)分別關于x和t求導,然后乘以utx,在[0,M]上積分得

M0+M1+M2。

(26)

這里

frtρ-1)utxdx。

參考文獻M0,M1的估計見[1]。

‖frr‖2+‖fr‖2)+‖ftx‖2+‖frt‖2，

則把M0,M1,M2的估計式代入式(26)得

‖frr‖2+‖fr‖2)+‖ftx‖2+‖frt‖2。

上式在[0,t]上積分,并利用引理1，2及條件(A3)得式(25)。

引理4

(27)

證 明式(6)關于x求三次導,得

6ρρxxuxx+6ρρxuxxx+2ρρxxxux+ρ2uxxxx=0。

(28)

式(28)兩端乘以2ρxxx,其結果在[0,M]上積分,然后通過分部積分,引理1和h?lder不等式得

12C1(T)‖ρx‖L∞‖ux‖L∞‖ρxx‖L2‖ρxxx‖L2+

12C1(T)‖ρxx‖L2‖ρxxx‖L2‖uxx‖L2+

12C1(T)‖ρx‖L∞‖ρxxx‖L2‖uxxx‖L2+

利用引理1,Cauchy不等式得

C2(T)‖uxxx‖2+C2(T)‖uxxxx‖2+C2(T)。

(29)

由式(7)得

(c2+2c1)ρ1+θuxx=ut+A(ργ)x-

(c2+2c1)(1+θ)ρθρxux+f。

(30)

式(30)兩端關于x求兩次導得

(c2+2c1)ρ1+θuxxxx=

-(c2+2c1)(1+θ)ρθρxuxxx+utxx+A(ργ)xxx-

ρθρxuxxx)-(c2+2c1)(1+θ)[ρθρxux]xx+

fxx+fxr(1+ρ-1)-frρ-2ρx+frrρ-1，

(31)

由式(31),條件(A3)，引理1，得到

(32)

由式(29)和式(32),引理3,Gronwall不等式得

(33)

由(17)和引理1,引理3得

(34)

由式(32),式(33)和式(34),引理3得

(35)

式(6)關于x求二次導得

(36)

式(6)關于t求導得

(37)

式(37)關于x求導得

2ρρxutx-ρ2utxx。

(38)

由式(36),式(37)和式(38),引理1～3,插值不等式得

‖utxx‖2ds)≤C4(T)。

引理5

(39)

證 明式(7)關于t求導,其結果平方,利用引理1～4,式(6)得

(40)

式(7)分別關于x,t求導,其結果平方,利用引理1～4,式(6),(40),條件(A3)得

引理6

‖ρxxxx‖2+‖uxxxx‖2+

(41)

證 明由式(19),引理4～5,條件(A3)得

C4(T)。

(42)

式(28)關于x求導其結果乘以ρxxxx,在[0,M]上積分，由引理1,引理3,引理4,Cauchy不等式得

‖uxxxxx‖2}+C1(T) ≤C1(T)‖ρxxxx‖2+

C1(T)‖uxxxxx‖2+C2(T)。

(43)

下面估計‖uxxxxx‖2。

式(31)關于x求導,由結果可以得到

‖uxxxxx‖2≤C1(T)(‖uxxxx‖2+‖utxxx‖2+

‖ρxxxx‖2+‖fxxx‖2+‖fxxr‖2+

‖fxrr‖2+‖frx‖2+‖frr‖2+‖frrr‖2)。

(44)

把式(44)代入式(43),利用條件(A3),Gronwall不等式得

(45)

由式(44),(45),引理4～5,條件(A3)得

由式(6),引理1～6可以得出下面的推論。

推論1

‖ρxxtt‖2)ds≤C4(T)。

(46)

引理7

(47)

證 明式(7)關于t求導兩次,其結果乘以uttt,然后分部積分,利用邊界條件(10),條件(A3),Cauchy不等式得

‖ρt‖2‖uxt‖2+‖frr‖2+‖frt‖2+

‖fr‖2‖ut‖2+‖ftt‖2)，

則

引理8

‖uxxxxt‖2)ds≤C4(T)。

(48)

證 明式 (7)關于x,t求導,得

式(7)關于x求導,t求導兩次，利用引理1～7，推論1得

式(7)關于x求導兩次,t求導，利用引理1～7，推論1得

引理9

(49)

證 明利用式(6),引理1～8，式(46)和插值不等式，能得到式(49)。

參考文獻：

[1]QIN Yu-ming， HANG Lan. Regularity of 1D compressible isentropic Navier-Stokes equations with density-dependent viscosity[J].J Differenital Equations,2008,245:3956-3973.

[2]WEN Huan-yao，ZHU Chang-jiang.Global classical large solutions to Navier-Stokes equations for viscous compressible and heat-conducting fluids with vacuum[J].SIAM J Math Anal,2013,45(2):431-468.

[3]DING S,WEN H,YAO L，et al. Global spherically symmetric classical solution to compressible Navier-Stokes equations with large initial data and vacuum[J].SIAM J Math Anal 2012,44(2):1257-1278.

[4]OKADA M,MATUSU-NECASOVA S,MAKINO T.Free bounary problem for the equations of one-dimensional motion of compressible gas with density-dependent viscosity[J].Ann Univ Ferrara Sez VII(N.S),2002,48:1-20.

[5]YANG T,YAO Z,ZHU C.Compressible Navier-Stokes equations with degenerate viscosity coefficient and vacuum[J].Comm Partial Differential Equations,2001,26:965-981.

[6]JIANG S,XIN Z, ZHANG P.Global weak solutions to 1D compressible isentropic Navier-Stokes equations with density-dependent viscosity[J].Appl Methods Anal,2005,12:239-252.

[7]YANG T,ZHAO H. A vacuum problem for the one-dimensional compressible Navier-Stokes equations with density-dependent viscosity[J].J Differential Equations,2001,184:965-981.

[8]FANG D, ZHANG T. Compressible Navier-Stokes equations with vacuum state in one dimension[J].Pure Appl Anal, 2004(3):675-694.

[9]FANG D, ZHANG T. A note on compressible Navier-Stokes equations with vacuum state in one dimension[J].Nonlinear Anal,2004,58:719-731.

[10]KONG Chun-xiang. Global existence behavior of the solutions for compressible flow[J].Henan Science,2013(11)：121-129.

(編輯亢小玉)

·學術動態·

第七批“百人計劃”西北大學入選人數再創新高

近日，陜西省委組織部公布了第七批陜西省“百人計劃”評選結果，西北大學23人入選，居全省各單位之首。

陜西省“百人計劃”項目設立于2009年，是陜西省為鼓勵和吸引高層次人才來陜西創業、工作、服務的一項高層次人才項目，主要分為全職項目、創業人才項目、青年項目、短期項目四種類型。項目設立以來，西北大學在前六批評選中，共獲批42人(全職項目18人、青年項目15人、短期項目9人)，加上第七批獲批的23人(全職項目6人、青年項目7人、短期項目10人)，共計獲批65人，獲批總人數為全省第一。

近年來，在陜西省委省政府的大力支持下，西北大學黨委和行政高度重視師資隊伍建設，校內各單位深入落實《西北大學“十二五”師資隊伍建設規劃》，西北大學師資隊伍建設工作不斷得到加強。

(薛鮑)