剪力釘剛度對組合梁斜拉橋受力性能的影響研究

黃永輝，黃超凡，黃志科

(廣州大學廣州大學－淡江大學工程結構災害與控制聯(lián)合研究中心，廣東廣州 510006)

鋼－混凝土組合結構是目前應用比較廣泛的新型結構，充分利用了混凝土的抗壓性能和鋼結構的抗拉性能.為使二者能夠更好結合充分發(fā)揮其性能，往往在鋼與混凝土界面加入例如剪力釘之類的剪力連接件.剪力連接件主要傳遞結合面的剪力，抵抗其在剪力作用下的變形，對結構的剛度和受力將產生較大的影響［1］.鋼－混凝土組合構件最早用于橋梁結構始于20世紀50年代［2］.鋼－混凝土組合結構橋梁(簡稱組合橋)是指將鋼梁與混凝土橋面板通過抗剪連接件連接成整體并考慮共同受力的橋梁結構形式［3］.相對于不按組合結構設計的純鋼橋，組合橋可以減小結構高度、提高結構剛度、減小結構在活載下的撓度.剪力連接件作為鋼－混凝土組合結構的重要構件，其剛度對結構的影響受到了很多學者的關注與研究.DOGAN等［4］做了6組相同的剪力釘推出實驗，對實驗構件施加相同的周期荷載.實驗發(fā)現(xiàn)在實驗中剪力釘?shù)膭偠入S著加載次數(shù)增加而逐漸減少.實驗結果表明通過評估剪力釘?shù)膭偠韧嘶軌蝾A測鋼－混凝土－鋼疊合體系的在周期荷載下的使用壽命.同濟大學的吳沖等［5］發(fā)現(xiàn)剪力釘通常受到雙軸的剪力及由于行車荷載產生的橫向彎矩，從而影響其受力性能.通過有限元方法分析了諸如剪力釘?shù)母叨取⒅睆降葏?shù)對剪力釘受力性能的影響.發(fā)現(xiàn)了直徑更大的剪力釘受雙軸剪力的影響比較小，初始彎矩產生的混凝土裂縫對剪力釘?shù)膭偠仁遣焕?同濟大學劉玉擎等［6］通過實驗研究了單釘剪力連接件和多釘剪力連接件的受力性能區(qū)別，發(fā)現(xiàn)單釘剪力連接件與多釘建立連接件具有相近的剛度，多釘剪力連接件的釘間距離對剛度的影響很小.單釘?shù)臉O限強度比多釘?shù)拇?0%左右，當荷載達到峰值時單釘?shù)南鄬浦当榷噌數(shù)拇?9%左右.徐驍青等［7］提出了剪力釘?shù)膭偠冗^大會導致組合梁結構中鋼與混凝土界面處的剪力的分布不均.為了解決這一問題，提出了用橡膠套裹住剪力釘以達到減小剪力釘剛度的效果.實驗發(fā)現(xiàn)和未進行處理的剪力釘比較，處理過的剪力釘?shù)目辜魪姸茸兓淮罂梢院雎裕羌袅︶數(shù)膭偠葏s明顯的減小了，受剪力學性能也隨之改變.綜上可知，對于剪力釘?shù)膭偠妊芯看蠖嗉性趯で笥绊懠袅︶攧偠鹊囊蛩兀鴮τ诩袅︶攧偠葘M合結構受力性能影響的參數(shù)分析較少，本文研究了不同剪力釘剛度對組合梁斜拉橋的受力性能的影響，從而為該類結構設計提供指導.

1 工程背景

該背景橋為雙索面獨塔組合梁斜拉橋，其跨度為2×100 m，橋塔、主梁、橋墩固結，采用雙柱式主塔，豎琴式雙索面斜拉索，橋寬20.1 m，橋型布置圖見圖1.工字型鋼梁作為主梁，橫梁、小縱梁通過節(jié)點板連接形成鋼構架，預制橋面板則架設在此鋼構架上，采用現(xiàn)澆膨脹混凝土濕接縫，通過剪力釘將混凝土橋面板和鋼主梁連接成一個整體.

圖1 某斜拉橋工程立面圖/mFig.1 Elevation of the bridge/m

2 剪力釘滑移本構關系

在眾多剪力釘荷載－滑移關系表達式中，OLLGAARD 等［8］提出的指數(shù)公式和 BUTTRY［9］的分數(shù)公式最具代表性，被廣大研究者所引用.

OLLGAARD提出的剪力釘荷載－滑移關系表達式如下:

式中，Δ表示滑移量(mm);Q表示剪力值(kN);Qu表示抗剪承載力設計值(kN).

BUTTRY提出的剪力釘荷載－滑移關系表達式如下:

式中，Δ表示滑移量(mm);Qu為剪力釘?shù)目辜舫休d力設計值(kN).

OLLGAARD和BUTTRY公式曲線對比見圖2，由圖2可知，盡管表達式不一樣，但兩者曲線的相差并不大.

采用全曲線模型在有限元建模時較難實現(xiàn)，一般均采用分段式模型.為簡化模型便于編程計算，有學者在實驗的基礎上提出了二折線或三折線模型來反映剪力釘荷載－滑移的非線性關系.其中最為經(jīng)典的為 OEHLERS二折線模型和CHANG三折線模型.

OEHLERS等［10］提出的剪力釘二折線荷載－滑移本構曲線見圖3.

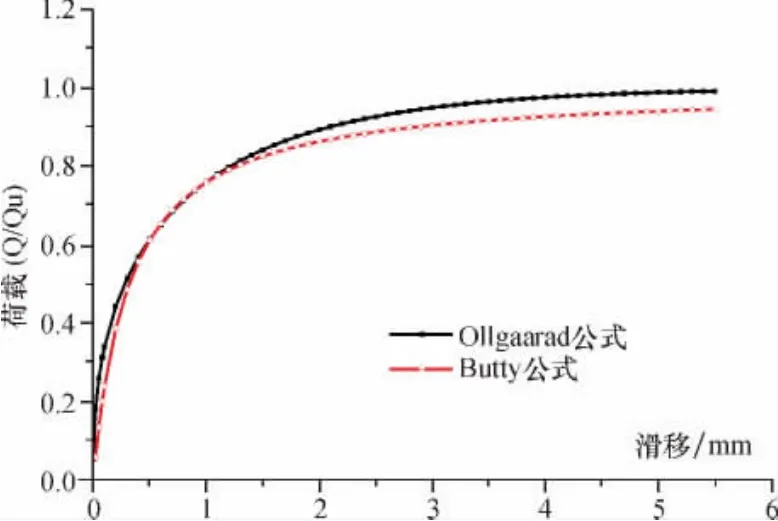
圖2 OLLGAARD和BUTTERY荷載－滑移曲線Fig.2 OLLGAARD and BUTTERY's Load-slip curves

彈性階段的剪切剛度為

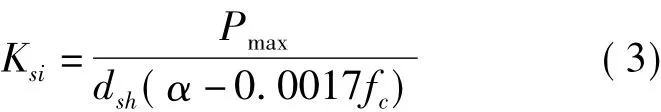
開始滑移點的滑移值為

極限滑移值為

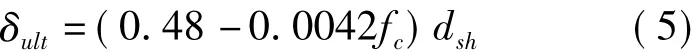
式中，Pmax表示剪力釘抗剪強度設計值(N);dsh表示剪力釘栓桿直徑(mm);fc表示混凝土抗壓強度設計值(MPa);α取值范圍為0.08～0.24.

CHANG等［11］提出的剪力釘三折線荷載－滑移本構曲線見圖4.但曲線中關鍵點的數(shù)值沒有給出理論計算公式，必須通過試驗獲得.

圖3 OEHLERS荷載－滑移曲線Fig.3 OEHLERS's Load-slip curve

圖4 CHANG荷載－滑移曲線Fig.4 CHANG's Load-slip curve

3 有限元模型的建立

采用ANSYS軟件建立有限元計算模型，其中，橋塔采用梁單元beam188模擬，拉索單元采用桁架單元Link10模擬，主縱梁，小縱梁、橫梁及橋面板均采用板殼單元shell63模擬，在鋼縱梁與橋面板結合的位置采用非線性彈簧單元Combin39模擬剪力釘，板殼單元和彈簧單元采用共節(jié)點的方式連接.

Combin39是一個具有非線性功能的彈簧單元，具有軸向或扭轉功能.軸向選項代表軸向拉壓單元，每個結點具有3個方向的平動自由度.圖5為Combin39單元的幾何參數(shù)圖.

由圖5可知，可以采用分段直線來模擬剪力釘?shù)暮奢d－滑移本構關系，因此，本文可采用OEHLERS方法來計算剪力釘?shù)暮奢d滑移曲線.

圖5 Combin39單元幾何參數(shù)圖Fig.5 Geometric parameters of Combin39

本次背景橋梁采用Φ22×200 mm剪力釘，各鋼梁采用的剪力釘布置見圖6，該橋共布置剪力釘49 754個.橋面板采用C50混凝土，其參數(shù)為Ec=34.5GPa，fc=23.1 MPa.

按OEHLERS方法計算可得，單個剪力釘?shù)暮奢d－滑移曲線見圖7.

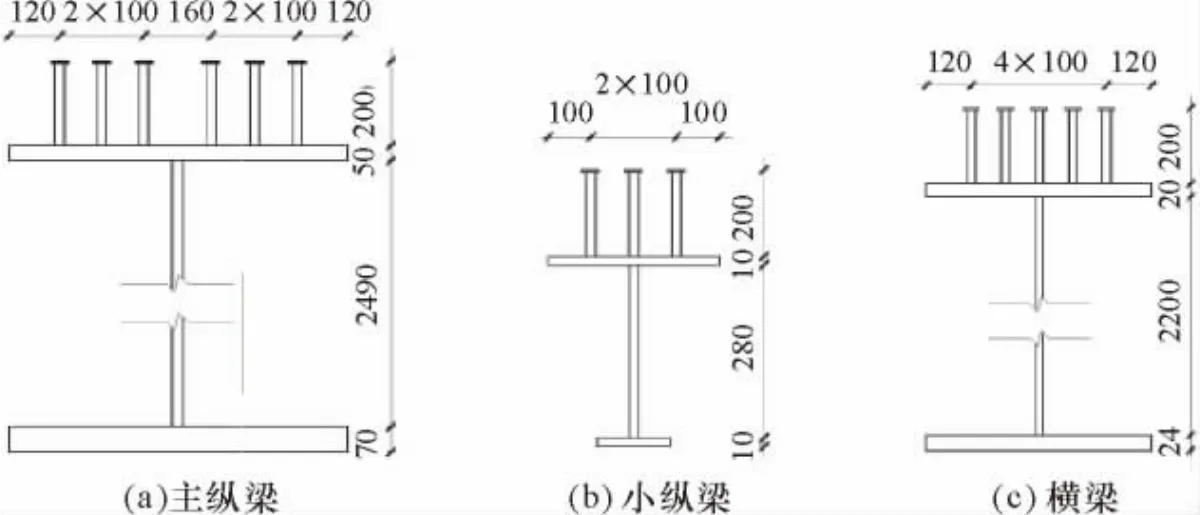
圖6 設計剪力釘布置圖/mmFig.6 Layout of stud shear connectors/mm

圖7 單個剪力釘?shù)暮奢d－滑移曲線Fig.7 Load-slip curve of single stud

為減小有限元模型的規(guī)模，從而提高計算速度，在建模時并不在所有剪力釘處劃分節(jié)點，而是將單元段內的所有剪力釘?shù)刃橐粋€剪力釘，這樣就減小了全橋模型的單元總數(shù).剪力釘?shù)牡刃偠葹?/p>

式中，nt為單元節(jié)段內剪力釘排數(shù)(橫向)，nl為單元節(jié)段內剪力釘列數(shù)(縱向)，Ke為單個剪力釘?shù)膭偠?

按照以上方法，建立好的有限元模型見圖8，加載示意見圖9.

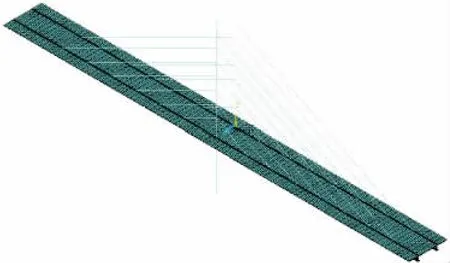
圖8 算例橋梁有限元計算模型Fig.8 Finite element model of the bridge

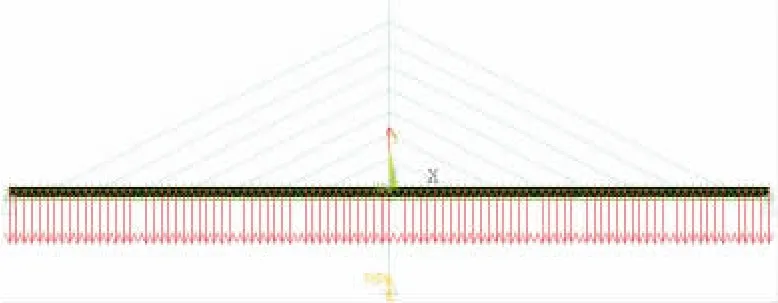
圖9 邊界條件及加載方式Fig.9 Boundary conditions and load arrangement

在本文的有限元計算模型中，主要分析以下兩種荷載工況:

(1)恒載工況:包括一期恒載和二期恒載;

(2)恒載+全橋均布車道荷載，右邊跨跨中作用集中力.

4 參數(shù)分析

4.1 剪力釘剛度對界面滑移值的影響

采用結構在工況1作用下的結果來分析不同的剪力釘剛度對界面滑移值的影響，其界面滑移值對比見圖10.由圖可知采用不同剛度的剪力釘時，界面滑移值沿橋縱向的分布規(guī)律是基本一致的.當采用0.5倍設計剛度和1倍設計剛度計算時界面滑移值都較小，且二者數(shù)值相差也很小，最大滑移不超過0.3 mm.當剛度小于0.3倍的設計剛度時，由圖可知滑移值會迅速變大，采用0.3倍設計剛度時最大滑移值為1.25 mm，采用0.1倍設計剛度時，最大滑移值為2.40 mm.

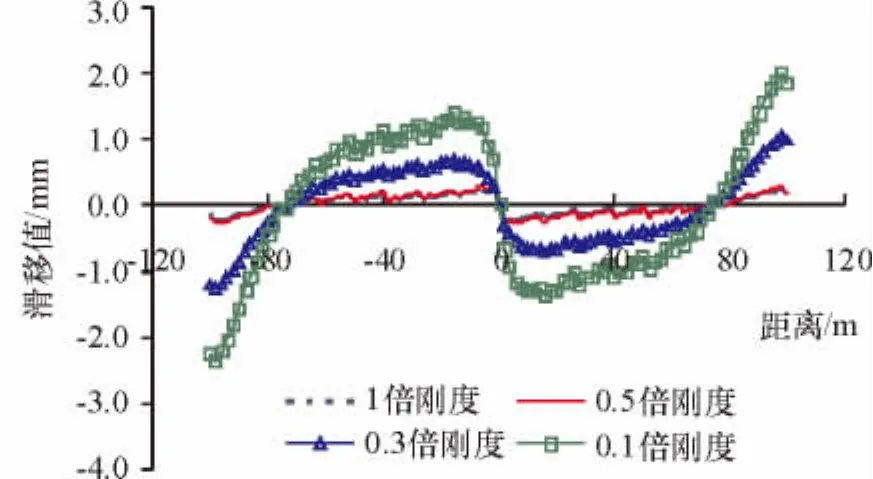
圖10 界面滑移值曲線對比圖Fig.10 Comparison of the interfacial slip curves

4.2 剪力釘剛度對位移的影響

不同剪力釘剛度模型對應的位移曲線見圖11，由圖可知橋梁模型的位移跟剪力釘剛度有著重要關系，剪力釘剛度的降低會使得橋梁的位移變大.當采用1倍設計剛度的剪力釘時，橋梁在工況1下的撓度最大值為0.18 m，當界面無剪力釘時，對應的最大撓度為0.22 m，撓度增幅達22.2%.

圖11 位移曲線對比圖Fig.11 Comparison of the displacement curves

4.3 剪力釘剛度對應力的影響

圖12、圖13分別為不同剪力釘剛度模型跨中截面的應變、應力圖.由圖12可知，隨著剪力釘剛度的減小，其應變分布規(guī)律偏離平截面假定越大.如果完全不考慮界面的粘結滑移，那么鋼梁底部拉應力為74.2 MPa，混凝土完全受壓.當布置設計剛度的剪力釘時，鋼梁底部拉應力為78.4 MPa，混凝土同樣也是完全受壓.當布置0.1倍設計剛度的剪力釘時，鋼梁上緣的壓應力區(qū)變大，最大壓應力超過了拉應力，且混凝土板下緣出現(xiàn)拉應力，這樣會大大削弱截面的整體剛度.由此可知，粘結滑移對組合梁橋應力分布有著非常重要的影響，剪力釘剛度對中和軸位置的影響同樣十分明顯，將導致鋼梁出現(xiàn)受壓，混凝土出現(xiàn)受拉的情況.設計時必須保證鋼－混凝土界面有足夠的粘結強度.

圖12 沿梁高應變分布曲線Fig.12 Strain distribution curve along the height of the beam

圖13 沿梁高應力分布曲線Fig.13 Stress distribution curve along the height of the beam

4.4 剪力釘剛度對極限承載力的影響

因為作用在橋梁結構上的荷載往往十分復雜，很難用統(tǒng)一的荷載集度來表示，而結構的極限承載力跟荷載的形式有很大的關系，這就使得定義極限承載力指標變得較為困難.本文參考文獻［12］，定義最大活載系數(shù)λmax和結構整體安全系數(shù)n2個參數(shù)來作為結構極限承載能力的指標.

不同剪力釘剛度模型的最大豎向撓度隨荷載的變化曲線見圖14.在工況2下的極限承載力計算結果見表1.

圖14 不同剪力釘剛度模型最大撓度－荷載曲線Fig.14 The maximum deflection-load curve of the models with different stud stiffness

表1 工況2極限承載力計算結果對比Table 1 Calculation results of ultimate bearing capacity of the bridge in load case 2

由表1可知，考慮粘結滑移時，對于采用0倍設計剛度、0.1倍設計剛度、0.5倍設計剛度、1倍設計剛度的模型，其最大活載系數(shù)分別為不考慮滑移模型的54%，71%，84%和91%，其結構整體安全系數(shù)分別為不考慮滑移模型的60%，65%，86%和95%，以上結果說明剪力釘剛度對組合梁斜拉橋的極限承載力有著重要影響.當采用0倍設計剛度時即混凝土板和鋼梁之間無剪力釘時，最大活載系數(shù)和結構整體安全系數(shù)減小約一半，表明剪力連接件的剛度對組合梁斜拉橋的極限承載能力影響較大.由圖14可知，不同剪力釘剛度對應的荷載位移曲線差別也較大，當布置大于0.5倍設計鋼度的剪力釘時，在荷載較小的情況下，考慮粘結滑移和不考慮粘結滑移模型剛度相差不大，當荷載增大到一定程度并引起剪力件滑移后，結構的整體剛度會有所下降.但是當剪力釘?shù)膭偠刃∮?.5倍設計剛度時，考慮粘結滑移和不考慮粘結滑移模型的荷載位移曲線在一開始就相差比較大.

5 結論

本文結合某斜拉橋實際工程，對剪力釘剛度對組合梁斜拉橋受力性能的影響進行了參數(shù)分析，得到了以下結論:

(1)采用不同的剪力釘剛度時，界面滑移值沿橋梁縱向的分布規(guī)律基本一致，但數(shù)值差別較大，界面滑移值隨著剪力釘剛度的減小而快速增大;

(2)剪力釘剛度對橋梁豎向撓度有重要影響，隨著剪力釘剛度的降低，橋梁的豎向撓度逐漸增大.當界面無剪力釘時，其跨中撓度增幅達22.2%.

(3)考慮剪力釘?shù)恼辰Y滑移后，應變沿梁高的分布規(guī)律不再滿足平截面假定，且偏離的程度隨著剪力釘剛度的減小而增大.剪力釘剛度對中和軸位置的影響也十分明顯，將導致出現(xiàn)鋼梁受壓，混凝土受拉的情況，組合梁橋設計時必須保證剪力釘有足夠的剛度.

(4)剪力連接件的剛度對組合梁斜拉橋的極限承載能力影響較大，當混凝土板和鋼梁界面無剪力釘時，結構的活載系數(shù)和整體安全系數(shù)減小約一半，當剪力件剛度小于設計剛度的0.5倍時，考慮粘結滑移和不考慮粘結滑移模型的荷載－位移曲線在一開始就相差比較大.

［1］ 藺釗飛，劉玉擎.焊釘連接件峰值滑移及剪力—滑移本構關系［J］.同濟大學學報:自然科學版，2014，42(7):1006-1010.LIN Z F，LIU Y Q.Peak slip and load-slip realationship of headed stud connectors［J］.J Tongji Univ:Nat Sci，2014，42(7):1006-1010.

［2］ OLLGAARD H G，SLUTTER R G，F(xiàn)ISHER J D.Shear strength of stud connectors in lightweight and normal-weight concrete［J］.Engin J Amer Instit Steel Constr，1971，8(2):55-64.

［3］ 聶建國，陶慕軒，吳麗麗，等.鋼-混凝土組合結構橋梁研究新進展［J］.土木工程學報，2012，45(6):110-122.NIE J G，TAO M X，WU L L，et al.Advances of research on steel-concrete composite bridges［J］.China Civil Engin J，2012，45(6):110-122.

［4］ DOGAN O，ROBERTS T M.Fatigue performance and stiffness variation of stud connectors in steel-concrete-steel sandwich systems［J］.J Constr Steel Res，2012，70(3):86-92.

［5］ CHEN X，KUNITOMO S，CHONG W，et al.Parametrical static analysis on group studs with typical push-out tests［J］.J Constr Steel Res，2012，72(5):84-96.

［6］ XUE D Y，LIU Y Q，YU Z，et al.Static behavior of multi-stud shear connectors for steel-concrete composite bridge［J］.J Constr Steel Res，2012，74(7):1-7.

［7］ XU X Q，LIU Y Q，HE J.Study on mechanical behavior of rubber-sleeved studs for steel and concrete composite structures［J］.Constr Build Mater，2014，53(2):533-546.

［8］ OLLGAARD J G，SLUTTER R G，F(xiàn)ISHER J W.Shear strength of stud connectors in lightweight and normal-weight concrete［J］.AISC Engin J，1971，8(2):55-59.

［9］ BUTTRY K E.Behavior of stud shear connectors in lightweight and normal-weight concrete［R］.Kansas:Missouri State Highway Department and University of Missouri-Columbia，1965.

［10］ OEHLERS D J.The stiffness of stud shear connections in composite beams［J］.J Constr Steel Res，1986，6(4):273-284.

［11］ SHIM C S，LEE P G，YOON T Y.Static behavior of large stud shear connectors［J］.Engin Struct，2004，26(12):1853-1860.

［12］滕啟杰.鋼管混凝土拱橋的極限承載力研究［D］.大連:大連理工大學，2007.TENG Q J.Study on the ultimate bearing capacity of concrete filled steel tube arch bridge［D］.Dalian:Dalian University of Technology，2007.