幾類(lèi)特殊和式極限求法的歸納

?

幾類(lèi)特殊和式極限求法的歸納

牛海軍

鐵嶺師范高等專(zhuān)科學(xué)校師范學(xué)院 (鐵嶺 112000)

摘 要對(duì)和式極限的求法進(jìn)行了歸納，介紹了利用夾逼定理、利用定積分定義、利用冪級(jí)數(shù)展開(kāi)式、利用數(shù)項(xiàng)級(jí)數(shù)收斂性等幾種常用的求和式極限的方法。

關(guān)鍵詞和式 極限 歸納

求極限是高等數(shù)學(xué)的重要內(nèi)容，求和式極限又是其中的一個(gè)難點(diǎn)，本文將常用的求和式極限的方法歸納一下。

1利用初等數(shù)學(xué)中的公式或技巧先求部分和再求極限

這種方法即利用數(shù)列中的一些已知的部分和公式或技巧(如裂項(xiàng)、乘系數(shù)等)來(lái)求和式極限。

例1：求極限

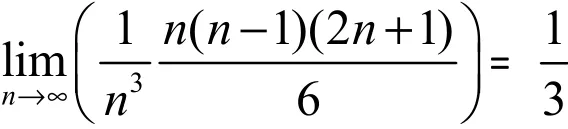
2　利用夾逼定理(即(“兩邊夾”法則)求和式極限

這種方法是將要求的和式適當(dāng)放大或縮小，再利用極限的夾逼定理來(lái)求極限。例2：求極限：

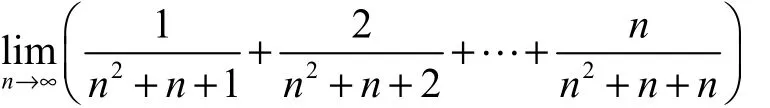
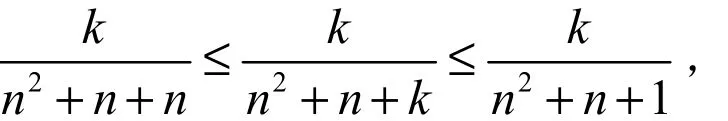
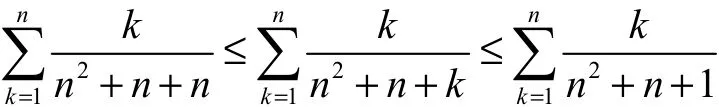
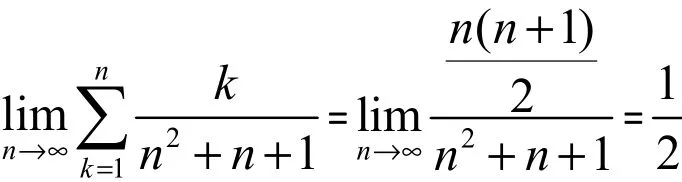
由夾逼定理，可得

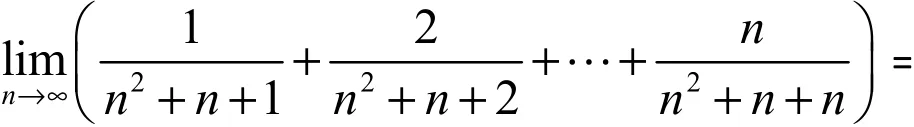
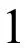
2。

3　利用定積分定義求和式極限

這種方法是根據(jù)定積分的概念將某些和式極限化為定積分定義中的積分和，再計(jì)算定積分求和式極限。例3 ：

解：

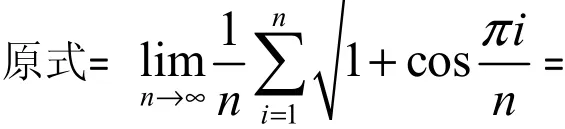
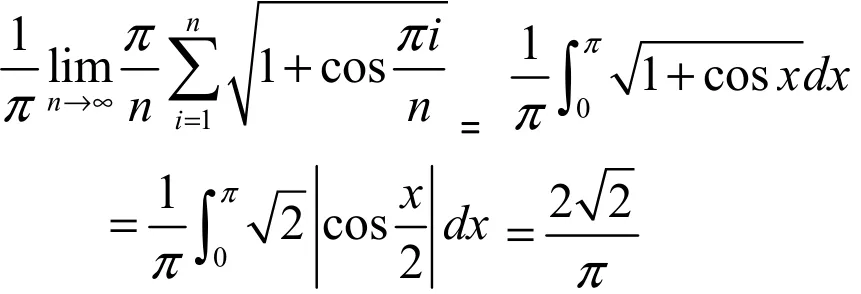
4　利用冪級(jí)數(shù)展開(kāi)式求和式極限

這種方法是利用在函數(shù)的冪級(jí)數(shù)(特別是麥克勞林)展開(kāi)式中選取適當(dāng)?shù)膞值來(lái)求和式極限。例4：求極限

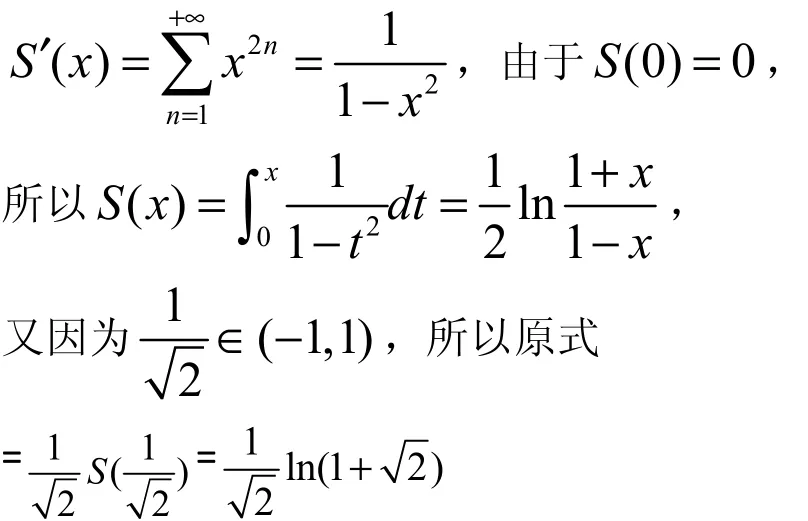
5　利用傅里葉級(jí)數(shù)展開(kāi)式求和式極限

這種方法是利用在函數(shù)的傅里葉(特別是正、余弦)展開(kāi)式，在其收斂域內(nèi)選取適當(dāng)?shù)膞值，即能轉(zhuǎn)化為通過(guò)對(duì)數(shù)項(xiàng)級(jí)數(shù)收斂的討論求和式極限。例5：求極限

f x= x展開(kāi)成余

弦級(jí)數(shù);

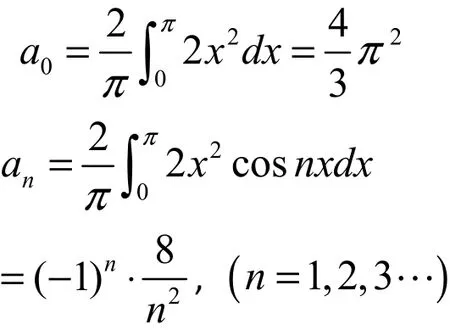
且該余弦級(jí)數(shù)在區(qū)間[?π , ]π上滿足狄利克雷充分條件，所以

6　利用(Stolz)定理求和式極限

Stolz定理：若數(shù)列{xn}和{yn}滿足以下條件：

(1)?自然數(shù)N0，當(dāng)n> N0時(shí)，yn+1> yn；

7　利用等價(jià)無(wú)窮小替換求和式極限

定理：p, q為兩個(gè)常數(shù)，且q >1?，則

解：由推論 原式

參考文獻(xiàn)

[1]同濟(jì)大學(xué)數(shù)學(xué)教研室.高等數(shù)學(xué)(第六版)[M].北京：高等教育出版社,2001.

[2]華東師范大學(xué)數(shù)學(xué)系.數(shù)學(xué)分析(上冊(cè)) 3 版)[M]. 北京: 高等教育出版社,2001.

[3]朱曉紅.關(guān)于和式極限求法的探討)[J].武漢工程職業(yè)技術(shù)學(xué)院學(xué)報(bào),2007,(3):74-76

[4]陳思源.關(guān)于和式極限的幾個(gè)重要定理及其應(yīng)用[J]. 河南科技,2010(4):394-396

[5]李冬梅.一類(lèi)特殊和式極限的簡(jiǎn)便求法)[J].鞍山師范學(xué)院學(xué)報(bào),2004,6 (4):1-13.

(責(zé)任編輯：文婷)