線性回歸模型的一種新有偏估計

?

線性回歸模型的一種新有偏估計

隋丹陽1鄂英力2

1遼寧裝備制造職業(yè)技術(shù)學院 (沈陽 110161) 2高明實驗學校(沈陽110000)

摘 要在線性回歸模型2下給出了有偏估計，其中K>0, c > 0為參數(shù)，?表示線性回歸模型的廣義最小二乘估計，討論了這種有偏估計的優(yōu)良性質(zhì)，得出了主要結(jié)論。

關(guān)鍵詞有偏估計 廣義最小二乘 嶺估計

0引言

考慮線性回歸模型：

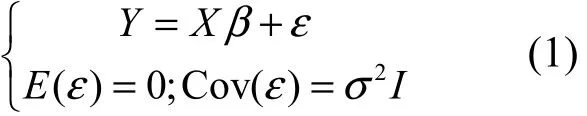
其中，Y是n×1觀測向量，X是n× p列滿秩設(shè)計陣，

β是p×1未知參數(shù)向量，ε為n×1隨機誤差向量。最小二乘估計是線性無偏估計類中方差最小的，但是當模型（1）存在復共線性時，最小二乘估計：

變得極不穩(wěn)定[1]，其均方誤差為XTX的特征

值）趨近于無窮大，LS估計的性能變得很差，特別是在經(jīng)濟問題中，回歸參數(shù)的經(jīng)濟意義往往得不到合理的解釋。近幾十年來，統(tǒng)計學家們針對最小二乘估計的改進做了很多研究，他們從消除多重共線性或減小估計的均方誤差出發(fā)，提出了各種新的估計方法，諸如嶺估計、壓縮估計、主成分估計、特征估計等。在實際應用中嶺估計無疑是最常用的一種有偏估計，因此人們對嶺估計的研究倍加重視，為了進一步改進它的性質(zhì)[2,3]，人們提出了種種修正嶺估計的方法，在一定條件下都可以優(yōu)于嶺估計。一般而言，對模型的限制越少越好，這樣在實際應用中適用的范圍才會更廣，并且在實際情況中，線性模型的誤差并不總是等方差且不相關(guān)的[4]。

1新估計的提出

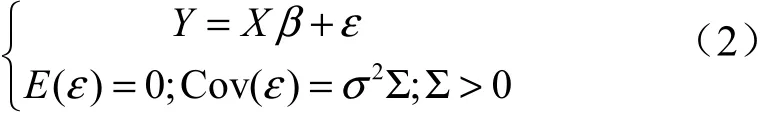
本文將模型推廣到奇異線性模型中：且模型（2）的廣義最小二乘估計[5]為。

為了便于討論這種估計的性質(zhì)，對模型（2）作一個適當?shù)淖兓海玫?/p>

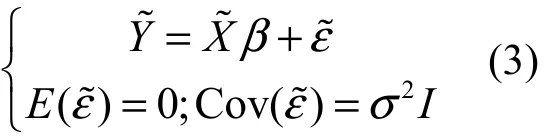
考慮模型（3）的典則形式：設(shè)2

1

p

λ λ λ

我們將對廣義嶺估計[6]做進一步改進，給出模型（2）的一個新估計：

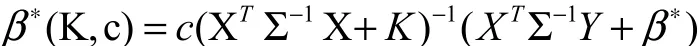
?的一些性質(zhì)

性變換。

證明：因為

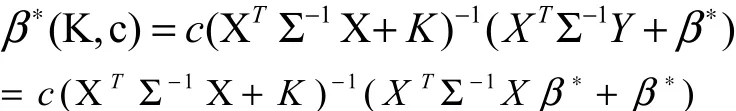
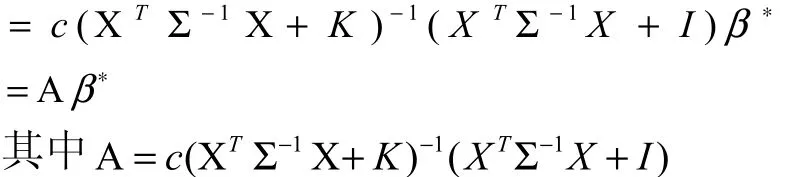
性質(zhì)2. β(K,c)

?是β?的有偏估計。證明：

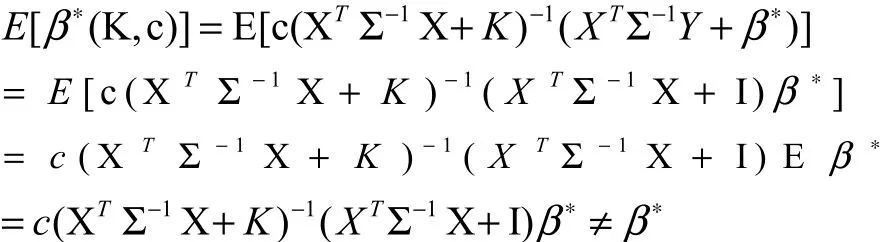
性質(zhì)3. 對任意的k> c >0，β?(K, c )是β?的壓縮，即

i。

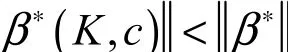
證明：對實對稱陣，T1X∑?X進行Schur分解。

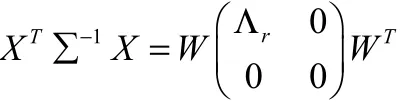
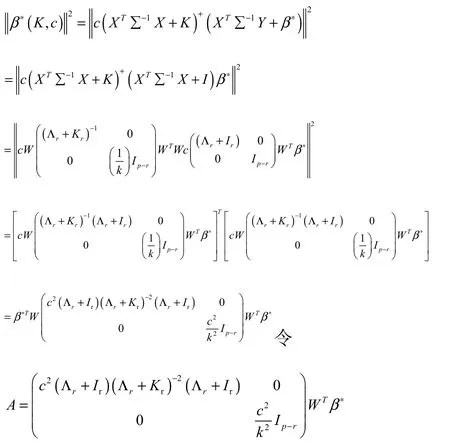
又因為0

因此，I? A>0，因為W為正交陣，所以有( )T0

可得

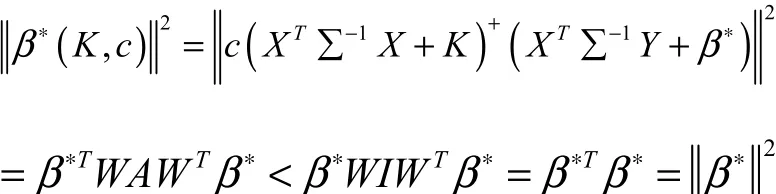
性質(zhì)4.對任意的0

i

k> c >，α(K,c)

?是α?向原點的壓縮。

證明：由模型（3）的典則形式可知

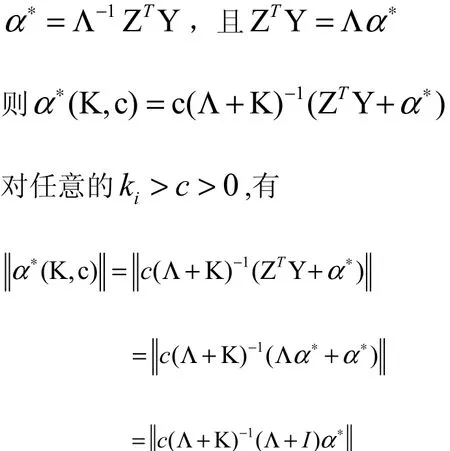
性質(zhì)5.

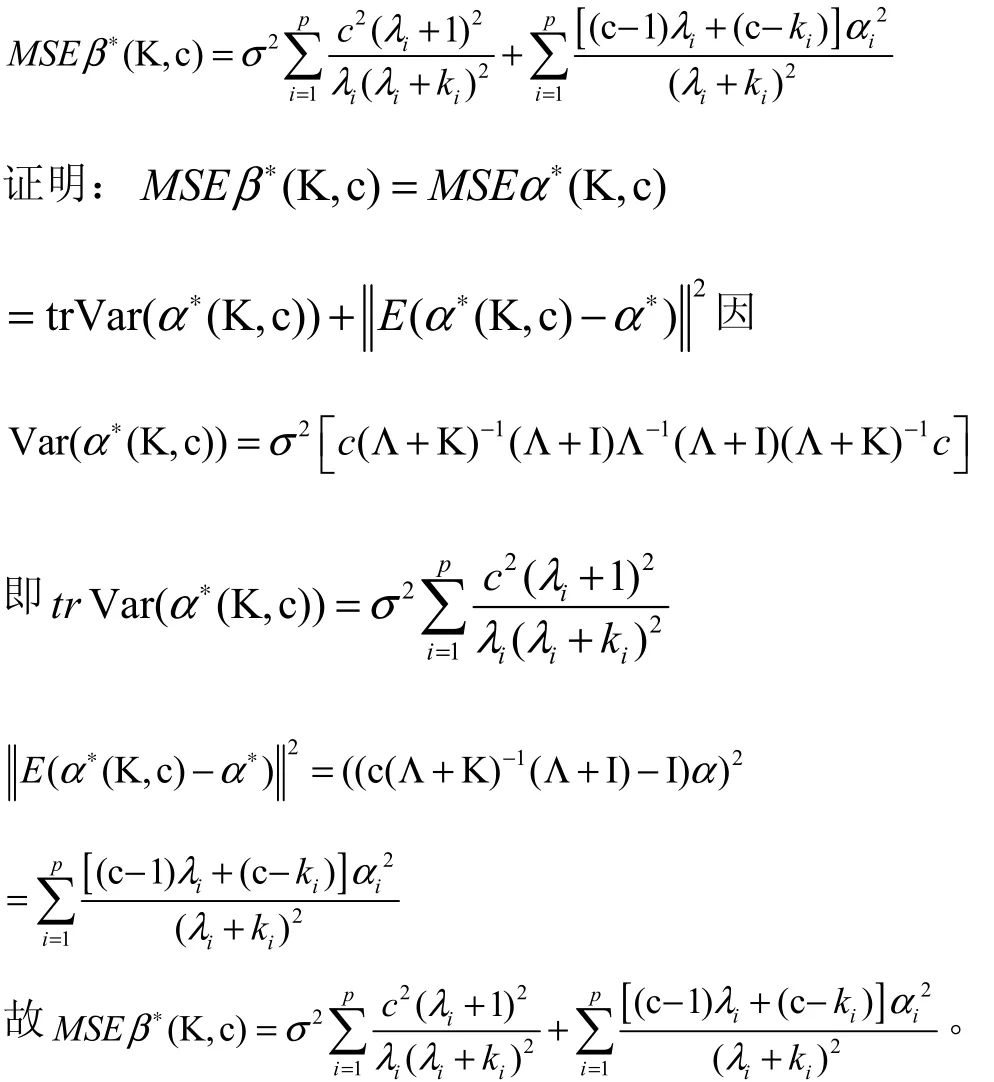
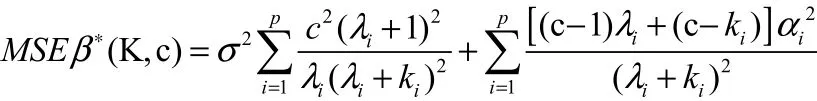
將上式分別對1,2, ,pk kk求偏導數(shù)，并令其為零，得

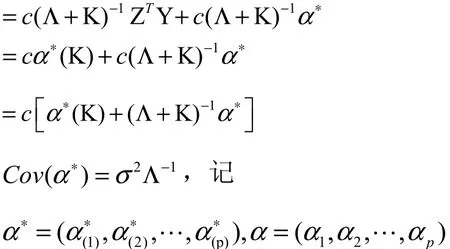
參考文獻

[1]王松桂.線性模型的理論及其應用[M].合肥：安徽教育出版社,1987.

[2]張建軍,吳曉平.線性回歸模型系數(shù)嶺估計的改進研究[J].海軍工程大學學報，2005,17(1):54-57.

[3]張偉. 線性回歸模型的一種有偏估計[J].武漢大學學報，2006,52(3):281-285.

[4]趙天璽，李兆勤.回歸系數(shù)的一種有偏估計[J].重慶工商大學學報.2007,24(6):541-614.

[5]王松桂,史建紅,尹素菊. 線性模型引論[M].北京:科技出版社,2005.

[6]郭效金.廣義嶺估計的新定義及其性質(zhì)[J].河南教育學院學報，2003,12（1）:35-36.

（責任編輯：林城）