Banach空間中混合均衡問題和相對擬非擴張半群公共解的一種逼近方法

李秀仁，王晶海

(福州大學數學與計算機科學學院，福建福州 350116)

0 引言

混合均衡問題是一類十分廣泛的均衡問題，它在非線性分析領域有著重要理論和應用價值．非線性分析領域中的許多問題都可以納入混合均衡問題的框架中加以研究，例如一般均衡問題、變分不等式問題、最優化問題和Nash均衡問題都是其特殊的情形．

設E為Banach空間，C為E的非空閉凸子集．設θ:C×C→R是一個均衡二元函數，即對任意的u∈C，θ(u，u)=0，φ:C→R是一個實值函數，混合均衡問題是求x∈C，使得MEP:θ(x，y)+φ(y)－φ(x)≥0，?y∈C．記Ω為混合均衡問題MEP(θ，φ)的解集．

由于混合均衡問題具有廣泛的應用，因而備受學者們的青睞．Fan L Y［1］在Hilbert空間中研究了混合均衡問題的解的存在性;Ceng等［2］通過使用KKM技術，得到混合均衡輔助問題的解的存在性和唯一性;文獻［3－5］分別用不同迭代方法討論并得到解的強收斂定理;Shioji等［6］在Hilbert空間中利用隱迭代，證明了在適當條件下序列{xn}強收斂于非擴張半群的不動點集中的一點;Suzuki［7］在Hilbert空間非擴張半群上利用隱迭代xn=αnu+(1－αn)T(tn)(xn)(n≥1)，證明了在適當條件下序列{xn}的強收斂性;2005年，Xu［8］將文獻［7］的結論推廣到具有弱連續的對偶映射的一致凸的Banach空間上;之后，Aleyner等［9］首次在一致光滑的Banach空間上利用顯迭代xn+1=αnu+(1－αn)T(tn)(xn)，n≥0，x0∈C，證明了在適當條件下序列{xn}的強收斂性;2007年，張石生等［10］在Banach空間上引入了一種新的非擴張半群的顯式復合迭代方法，并證明了其在適當條件下的強收斂性;2010年，唐金芳［11］在Hilbert空間中引進并研究了一種新的迭代算法，借以尋求混合均衡問題解集與非擴張半群不動點集的公共元;2011年，Ceng和Guu［12］在一致光滑和一致凸的Banach空間上建立一種求解廣義均衡問題和一族可數的相對非擴張映射不動點問題及極大單調算子的公共解的混合收縮投影算法;2012年，馬樂榮等［13］在Hilbert空間中，設計了兩種新的關于Meir－Keeler壓縮映像的粘滯型迭代算法，用以逼近非擴張半群的公共不動點，在適當的條件下，利用所提出的算法證明了非擴張半群公共不動點的強收斂定理;同年，Chang等［14］在Banach空間的框架下，借助修正的Halpern－Mann迭代算法，求解全局漸進擬φ非擴張半群的解集，并在適當的條件下，證明了該迭代序列的強收斂性;近來，Wattanawitoon［15］在Banach空間中通過一種混合投影算法尋求均衡問題和兩個相對擬非擴張映射的不動點，使研究的范疇更廣泛;2011年，Cholamjiak和Suantai［16］在Banach空間中，建立了逼近混合均衡問題和一可數族非擴張映射的公共解的迭代算法，并證明了算法的強收斂和弱收斂定理．

本文在Banach空間中，通過建立一種新的迭代算法，研究混合均衡和相對擬非擴張半群的不動點的公共解問題，得到該算法所產生的迭代序列的強收斂定理．

1 預備知識

為解出混合均衡問題，假設二元函數θ滿足下列條件:

(A1)θ(x，x)=0(?x∈ C);

(A2)θ為單調的，即θ(x，y)+θ(y，x)≤0(?x，y∈C);

(A3)θ(x，y)關于第一變量x為弱上半連續;

(A4)θ(x，y)關于第二變量y為凸和下半連續．

設U={x∈E:x=1}為E的單位球．稱Banach空間E為嚴格凸的如果對所有x，y∈U，x≠y有

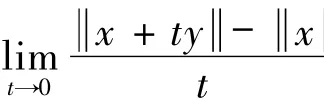
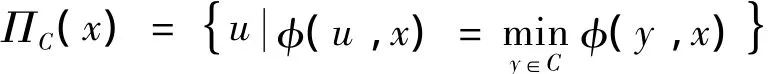
易見，若E為Hilbert空間，則φ(x，y)= x－y2，?x，y∈H，且廣義投影算子ΠC就是通常的投影算子．廣義投影算子ΠC的存在性和唯一性可參考文獻［16－19］．同時從函數φ(x，y)的定義可得

1)(y － x)2≤ φ(y，x)≤(y+x)2，?x，y∈E;

2)φ(x，y)= φ(x，z)+ φ(z，y)+2〈x － z，Jz－ Jy〉，?x，y，z∈E;

3)若E為一致凸和光滑的Banach空間，對所有x，y∈E有φ(x，y)=0當且僅當x=y;

4)φ(x，y)=〈x，Jx－Jy〉+〈y－x，Jy〉≤ x Jx－Jy+ y－x y，?x，y∈E．

設E*為E的對偶空間，C?E，T:C→C，若 Tx－Ty≤ x－y，?x，y∈C則稱映射T為非擴張．點x∈C使得Tx=x則稱x為T的不動點．用F(T)表示T的不動點集，即F(T)={x∈C:Tx=x}．若C中有一序列{xn}且該序列弱收斂于點ω∈C使得極限xn－Txn=0，則稱點ω是T的漸近不動點．用(T)表示T的漸近不動點集．稱T為相對非擴張的，若(T)=F(T)且對所有點x∈C及ω∈F(T)有φ(ω，Tx)≤φ(ω，x)．稱T為φ－非擴張的，若對任意x，y∈C有φ(Tx，Ty)≤φ(x，y)．稱T為相對擬非擴張的，如果F(T)≠Φ且對任意的x∈C，ω∈F(T)有φ(ω，Tx)≤φ(ω，x)．稱T為穩定非擴張(firmly－nonexpansive)，若對所有的x，y∈E有

設C為E的非空閉凸子集，一族映射{T(t):C→C，t≥0}，稱該族映射為C上的相對擬非擴張半群．如果以下條件滿足:

1)對任意的t1，t2∈R+，x∈C有T(t1+t2)x=T(t1)T(t2)x;

2)對任意的x∈C有T(0)x=x;

3)對任意的x∈C有t|→T(t)x是連續的;

4)F≠Φ，且對任意的t∈R+，x∈C，ω∈F有φ(ω，T(t)x)≤φ(ω，x)．其中:F:={x∈E:T(t)x=x，t≥0}=∩t≥0F(T(t))為映射族{T(t):C→C，t≥0}的公共不動點集．

引理1［16］設C為光滑的一致凸的Banach空間的非空有界閉凸子集，θ:C×C→R是一個均衡二元函數且滿足上述(A1)－(A4)條件，φ:C→R是一個實值函數且為凸下半連續．對任意r＞0，x∈E，定義映射Sr:E→2C:

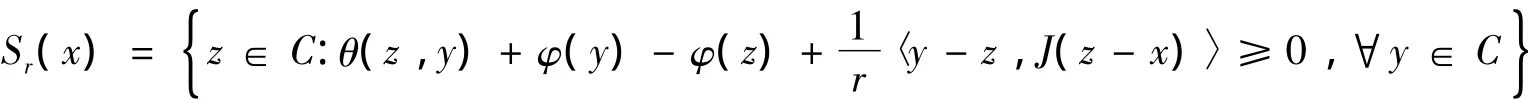
則下述情況都成立:

1)對每個x∈E，Sr(x)≠Φ;

2)Sr是單值的;

3)〈Srx－Sry，J(Srx－x)〉≤〈Srx－Sry，J(Sry－y)〉，對任意x，y∈E;

4)F(Sr)=MEP(θ，φ);

5)MEP(θ，φ)是非空閉凸的．

引理2［20］設C為光滑的一致凸的Banach空間的閉凸子集，θ:C×C→R是一個均衡二元函數且滿足上述(A1)－(A4)條件，φ:C→R是一個實值函數，r＞0．如果Sr為穩定非擴張，則對x∈E，ω∈F(Sr)有

引理3［21］設C為光滑的Banach空間的非空閉凸子集，x∈E，則x0=ΠCx當且僅當〈x0－y，Jx－Jx0〉≥0，?y∈ C．

引理4［21］設E為自反，嚴格凸和光滑的Banach空間，C為E的非空閉凸子集，x∈E，則φ(y，ΠCx)+φ(ΠCx，x)≤ φ(y，x)，?y∈C．

引理5［22］設E為一致凸和光滑的Banach空間，{xn}，{yn}為E中兩個序列，若φ(xn，yn)→0，且{xn}有界或{yn}有界，則xn－yn→0．

引理6［23］設E為一致凸和光滑的Banach空間，C為E的閉凸子集，T:C→C為閉的相對擬非擴張映射，則F(T)為C的閉凸子集．

引理7［24］設E為一致凸的Banach空間，Br(0)為E的閉球，則存在一個連續嚴格遞增凸的泛函g:［0，∞)→［0，∞)，g(0)=0，使得對任意x，y∈Br(0)有

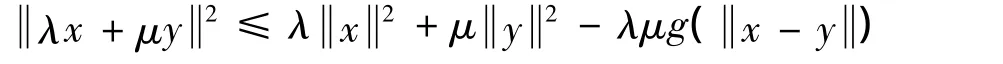
其中:λ，μ∈［0，1］且 λ+μ =1．

引理8［22］設E為光滑一致凸的Banach空間，r＞0，則存在一個嚴格遞增連續且凸的泛函g:［0，2r］→R，使得g(0)=0，且對任意x，y∈Br(0)有g(x－y)≤φ(x，y)．

引理9［25］設E*為一致凸的Banach空間，J為E的對偶映射，則J為單值的且在E的有界子集上一致連續，即B為E的有界子集，ε＞0，存在δ＞0，使得對任意x，y∈B， x－y ＜δ，有 J(x)－J(y) ＜ε．

2 主要結果

定理1 設E為一致光滑和一致凸的Banach空間，C為E的非空閉凸子集，θ:C×C→R是一個均衡二元函數且滿足上述(A1)－(A4)條件，φ:C→R為凸下半連續實值函數，W ={T(t):t≥0}為E中相對擬非擴張半群．設{xn}，{yn}，{zn}，{un}四個序列如下定義:

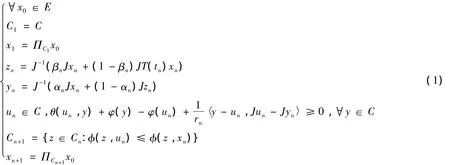
其中:J為E的正規對偶映射，un=Srnyn，序列{αn}，{βn}?(0，1)，對某個a＞0，有{rn}?［a，∞)，{tn}?［0，∞)為遞增且tn=∞．如果對rn＞0，Srn為穩定非擴張，且Γ:=F()∩MEP(θ，φ)=F(T(t))∩Ω≠Φ，那么序列{xn}，{un}強收斂于ω∈Γ，其中ω =ΠΓx0．

證明 分以下六步驟完成定理的證明．

第一步，證明對任意的n≥0，Cn是閉凸集．顯然C1=C是閉凸的，假設對某個k∈N，Ck是閉凸的，對于z∈ Ck使得φ(z，uk)≤φ(z，xk)，其等價于2(〈z，Jxk〉－〈z，Juk〉)≤ xk2－ uk2，可得 Ck+1是閉凸的．因此對所有的n≥0，Cn是閉凸集，這表明ΠCn+1x0是有定義的．

第二步，證明對任意的n≥0，Γ?Cn．顯見Γ?C1=C，假設對某個k∈N，Γ?Ck，則對任意的p∈Γ?Ck有:

及

由引理2可知，若Srn為穩定非擴張，則Srn為相對擬非擴張，考慮un=Srnyn，有φ(p，uk)=φ(p，Srkyk)≤φ(p，yk)≤ φ(p，xk)，即 p∈ Ck+1．因此，Γ ?Cnn=0，1，2，…．

第三步，證明{xn}為Cauchy列．由xn=ΠCnx0，則對任意z∈Cn，p∈Γ，有〈xn－z，Jx0－Jxn〉≥0及〈xn－p，Jx0－Jxn〉≥0．由引理4，當n≥1有 φ(xn，x0)= φ(ΠCnx0，x0)≤φ(p，x0)－φ(p，xn)≤φ(p，x0)，因此序列{φ(xn，x0)}有界．由xn= ΠCnx0，有φ(xn，x0)≤φ(xn+1，x0)，則序列{φ(xn，x0)}非遞減數列，從而φ(xn，x0)存在．由Cn的結構知，對任意正整數m≥n，有Cm?Cn，xm=ΠCmx0∈Cn，則 φ(xm，xn)= φ(xm，ΠCnx0)≤φ(xm，x0)－φ(ΠCnx0，x0)= φ(xm，x0)－φ(xn，x0)，令m，n→0有φ(xm，xn)→0．根據引理5可得，當m，n→0有xm－xn→0．由此可見，{xn}為Cauchy列．設xn→ω∈C．

移項可得(1－αn)βn(1－βn)g(JT(tn)xn－Jxn)≤φ(p，xn)－φ(p，un)．另一方面有:

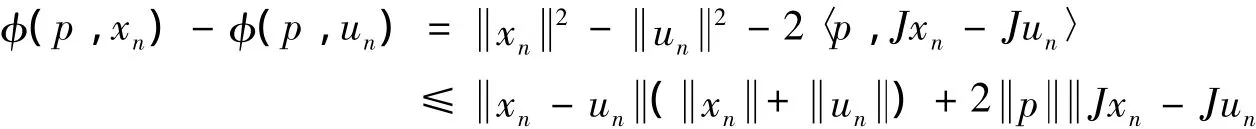
第五步，證明ω∈MEP(θ，φ)=Ω =F(Sr)．由Cn的結構可知φ(z，un)≤φ(z，xn)，又因un=Srnyn和引理2可得:

φ(un，yn)= φ(Srnyn，yn)≤φ(p，yn)－ φ(p，Srnyn)≤φ(p，xn)－ φ(p，Srnyn)= φ(p，xn)－ φ(p，un)當n→∞ 時φ(p，xn)－φ(p，un)→0，所以當n→∞ 時φ(un，yn)→0．由引理5得yn－ un=0，所以Jyn－Jun=0，從而，．另外，u=Sy有 θ(u，y)+φ(y)－ φ(u)+

nrnnnn〈y－un，Jun－Jyn〉≥0，?y∈C，由于θ的單調性和φ的下半連續性，注意到

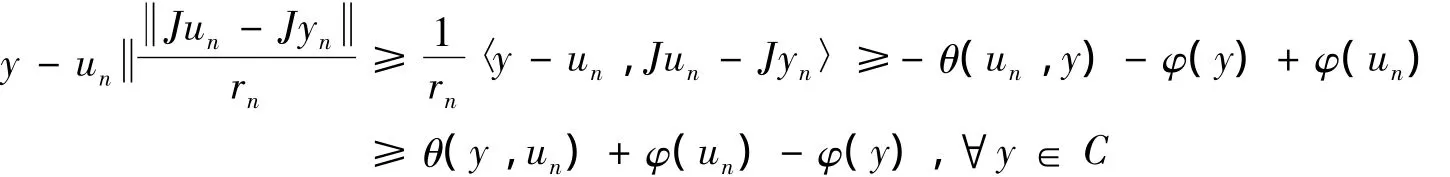
當n→∞ 時，un→ω，θ(x，y)關于第二變量凸下半連續性，所以θ(y，ω)+φ(ω)－φ(y)≤0，即θ(ω，y)+φ(y)≥φ(ω)，?y∈C，則可得ω∈MEP(θ，φ)=Ω =F(Sr)．綜上可知ω∈Γ．

第六步，證明ω =ΠΓx0．因xn=ΠCnx0，對所有的z∈Cn，有〈xn－z，Jx0－Jxn〉≥0且對任意的p∈ Γ，有〈xn－p，Jx0－Jxn〉≥0，則可知〈ω －p，Jx0－Jω〉≥0，?p∈Γ，再根據引理3可得ω =ΠΓx0．

綜上所述，定理1證明完畢．