線性模型的新的兩參數估計

薛美玉，梁飛豹

(福州大學數學與計算機科學學院，福建福州 350116)

0 引言

線性模型是現代統計學中應用最為廣泛的模型之一［1］．它在生物、醫學、金融、地質、國防等領域都有廣泛的應用．統計學家對線性模型作了大量研究，并出現了許多研究分支．其中，參數估計一直是一個非常活躍的分支．最小二乘估計(LS估計)因其優良性而在線性模型參數估計中占有重要地位［2］．但是，當數據具有復共線性時，LS估計變得不再優良．人們為此作了許多改進工作，例如，Stein于1960年提出了 Stein壓縮估計［3］，Hoerl和 Kennard于1970 年提出了嶺估計［4］，Liu于 1993 年提出了 Liu估計［5－6］，Ozkale和Kaciranlar于2007年提出了兩參數估計［7］，等等．

結合前人對LS估計的這些改進工作，提出線性模型參數估計的一種新方法——新的兩參數估計，并通過與最小二乘估計及舊的兩參數估計的比較，提出該估計的優越性．這里，為了便于比較，把文獻［7］Ozkale和Kaciranlar提出的兩參數估計稱為舊的兩參數估計，記為OTP估計，而把本文提出的新的兩參數估計記為NTP估計．

1 新的兩參數估計及其優良性

線性模型的一般形式為:

其中:Y是n×1可觀測向量;X是n×p列滿秩已知設計矩陣;β是p×1未知參數向量;ε是n×1隨機誤差向量;In是n階單位陣［8］．

定義1 稱 β^NTP=(XTX+kI)－1(XTX+dI)β^

LS為模型(1)中β的新的兩參數估計，其中，k＞d＞0，β^

LS=(XTX)－1XTY為β的最小二乘估計．

下面研究新的兩參數估計β^NTP的一些性質．為了表達方便，引入記號XTX=S和XTX+kI=Sk．那么，最小二乘估計 β^LS=S－1XTY，新的兩參數估計 β^NTP=Sk－1Sdβ^LS，舊的兩參數估計 β^OTP=(XTX+kI)－1(XTX+kdI)β^LS=Sk－1Skdβ^LS．

性質1 β^NTP是 β^LS的一個線性變換．

性質2 β^NTP是β的有偏估計．因為對任意k＞d＞0，E(β^NTP)=Sk－1Sdβ ≠ β．

性質3 當 β^LS≠0時，對任意k＞d＞0，總有 β^NTP＜ β^LS．表明 β^NTP是 β^LS向原點的一個壓

LSNTPLSNTPLS縮．

以上是 β^的一些基本性質，這些基本性質說明當存在復共線性時，β^改進了LS估計．此外，β^

NTPNTP

NTP還具備一些優良性．

定理1 β^是βNTP的可容許估計．

證明 因為β^NTP=Aβ^LS=Sk－1Sdβ^LS，由 Rao的定理［9］可得:

所以，對于任意k＞d＞0，β^NTP是β的可容許估計．

定理2 當(k－d)βTβ≤2σ2時，有:

1)MSEM(β^)＜ MSEM(β^);

NTPLS

2)GMSE(β^)＜ GMSE(β^);

NTPLS

3)MSE(β^)＜ MSE(β^)．

NTPLS

其中:MSEM(β^)、GMSE(β^)、MSE(β^)分別為β^的均方誤差矩陣、廣義均方誤差、均方誤差．

NTPNTPNTPNTP

證明 由于1)、2)、3)的等價性，只證1)．

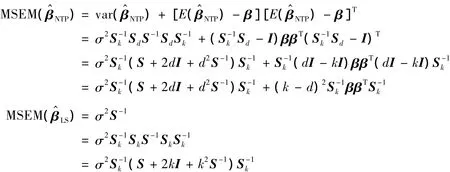
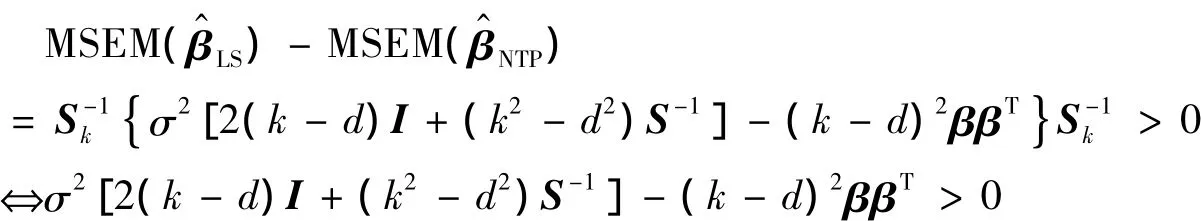
當k＞d＞0時，上式的一個充分條件是2σ2I－(k－d)ββT≥0，即(k－d)βTβ≤2σ2，從而定理得證．

定理3 當［2k－ (k+1)d］βTβ ≤2σ2時，有 MSEM(β^NTP)＜ MSEM(β^OTP)．

證明

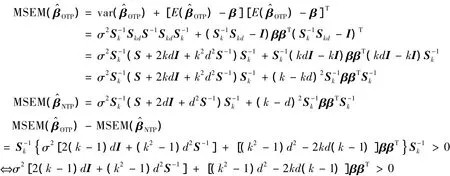
當k ＞ d ＞ 0，k ＞ 1時，上式等價于σ2［2I+(k+1)d S－1］+［(k+1)d－2k］ββT＞ 0，而該式的一個充分條件是2σ2I－［2k－(k+1)d］ββT≥0，即［2k－(k+1)d］βTβ≤2σ2，從而定理得證．

2 結論與展望

由于線性模型的廣泛應用，提出了線性模型參數的一種新的估計——新的兩參數估計:

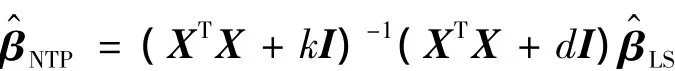
并討論了它的若干性質．例如，它是最小二乘估計的線性變換，具有有偏性、壓縮性、可容許性．比較突出的是，在均方誤差矩陣的意義下，證明了新的兩參數估計的優良性．但是，由于定理2和定理3所給的充分條件中含有未知參數β和σ2，所以需要用迭代的方法來確定k和d，這是筆者接下來要考慮的一方面．另外，β^NTP的大樣本性質，如相合性和漸進正態性，也是筆者后續工作中要考慮的另一方面．