多目標(biāo)聯(lián)盟競(jìng)賽算法

盧協(xié)平，劉秉瀚

(福州大學(xué)數(shù)學(xué)與計(jì)算機(jī)科學(xué)學(xué)院，福建福州 350116)

0 引言

聯(lián)盟競(jìng)賽算法［1］(league championship algorithm，LCA)是一種基于迭代的群體智能優(yōu)化算法．該算法的思路來(lái)源于體育團(tuán)隊(duì)在聯(lián)盟競(jìng)賽中的比賽現(xiàn)象．文獻(xiàn)［1］中的實(shí)驗(yàn)結(jié)果表明，聯(lián)盟競(jìng)賽算法相比粒子群優(yōu)化算法，無(wú)論從計(jì)算效果還是計(jì)算效率都有一定的優(yōu)勢(shì)．目前國(guó)內(nèi)外對(duì)該算法的研究主要包括:將算法擴(kuò)展為能夠解決約束優(yōu)化問(wèn)題的算法［2－3］和解決組合優(yōu)化問(wèn)題的離散算法［4］．

多目標(biāo)優(yōu)化問(wèn)題(multiobjective optimization problems，MOP)是指同時(shí)優(yōu)化多個(gè)目標(biāo)的問(wèn)題．一般情況單個(gè)目標(biāo)之間相互矛盾，使得不可能存在單個(gè)絕對(duì)最優(yōu)解，而是存在一個(gè)解集，稱為Pareto最優(yōu)解集(pareto optimal set)或非支配解集(nondominated set)．目前解決多目標(biāo)優(yōu)化問(wèn)題的常見(jiàn)方法是使用進(jìn)化算法，較為經(jīng)典的有Horn等提出的NPGA［5］，Knowles等提出的AGA［6］，Deb等提出的快速非支配排序遺傳算法NSGA－Ⅱ［7］以及近年Zhang等提出的一種新穎的基于分解的多目標(biāo)進(jìn)化算法MOEA/D［8］．這些算法使用Pareto支配關(guān)系指導(dǎo)算法搜索MOP的最優(yōu)解集，對(duì)一些測(cè)試問(wèn)題能夠取得不錯(cuò)的效果．但也存在不足，普遍表現(xiàn)在收斂速度慢，且求解非凸多峰多目標(biāo)測(cè)試函數(shù)(如ZDT4或DTLZ1)時(shí)效果較差．

本文提出多目標(biāo)聯(lián)盟競(jìng)賽算法(multiobjective league championship algorithm，MOLCA)，將聯(lián)盟競(jìng)賽算法擴(kuò)展為解決多目標(biāo)優(yōu)化問(wèn)題的算法，根據(jù)Pareto支配關(guān)系重新定義原算法在團(tuán)隊(duì)陣型比賽輸贏的判斷，并提出優(yōu)解擴(kuò)散策略使算法不輕易陷入局部最優(yōu)解．最后結(jié)合優(yōu)解擴(kuò)散策略開(kāi)關(guān)和分布性指標(biāo)使算法自動(dòng)停止運(yùn)行，避免不必要的算法迭代．實(shí)驗(yàn)結(jié)果表明，多目標(biāo)聯(lián)盟競(jìng)賽算法在求解大部分測(cè)試函數(shù)時(shí)，其收斂性指標(biāo)、分布性指標(biāo)和函數(shù)評(píng)價(jià)次數(shù)普遍比NSGA－Ⅱ和MOEA/D算法更有優(yōu)勢(shì)．

1 多目標(biāo)優(yōu)化問(wèn)題

以最小化多目標(biāo)問(wèn)題為研究對(duì)象．一個(gè)無(wú)約束的具有n維決策變量，m維子目標(biāo)的多目標(biāo)優(yōu)化問(wèn)題可表述為:

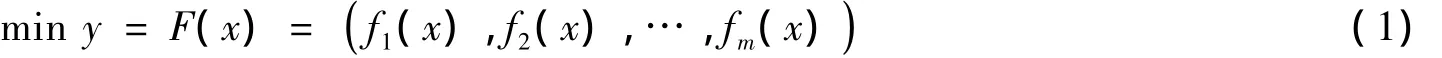
其中:x=(x1，…，xn)∈X?Rn為n維決策矢量，X為n維決策空間;y=(y1，…，ym)∈Y?Rm為m維目標(biāo)矢量，Y為m維的目標(biāo)空間，給出幾個(gè)重要定義．

定義1 Pareto占優(yōu)．設(shè)x1，x2∈X是式(1)的兩個(gè)可行解，則稱x1Pareto占優(yōu)x2，當(dāng)且僅當(dāng)

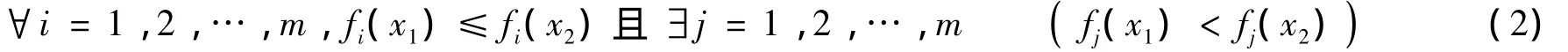
記作x1＞x2，也稱x1支配x2．

定義2 Pareto最優(yōu)解．解x*∈X稱為Pareto最優(yōu)解(或非支配解)，當(dāng)且僅當(dāng):

定義3 Pareto最優(yōu)解集．即所有Pareto最優(yōu)解的集合，定義如下:

Pareto占優(yōu)機(jī)制是目前最具代表性的占優(yōu)機(jī)制，且當(dāng)前大部分多目標(biāo)進(jìn)化算法都是基于該占優(yōu)機(jī)制，即把尋找Pareto最優(yōu)解集作為多目標(biāo)算法的最終目標(biāo)．本文的算法也不例外．

2 聯(lián)盟競(jìng)賽算法

2．1 聯(lián)盟競(jìng)賽算法基本流程

步驟1:初始化團(tuán)隊(duì)數(shù)量、團(tuán)隊(duì)陣型、比賽輪數(shù)S等，令當(dāng)前迭代次數(shù)t=0;

步驟2:產(chǎn)生一個(gè)賽季的比賽賽程;

步驟4:根據(jù)第t輪的比賽賽程進(jìn)行比賽，并按照一定規(guī)則判斷比賽輸贏;

步驟5:t=t+1，若t＞S，執(zhí)行步驟9;

步驟6:更新團(tuán)隊(duì)陣型:每個(gè)團(tuán)隊(duì)產(chǎn)生一個(gè)新陣型，若新陣型適應(yīng)值比當(dāng)前陣型適應(yīng)值更優(yōu)，則替換當(dāng)前陣型;

步驟7:若要產(chǎn)生新賽程，則根據(jù)某種規(guī)則產(chǎn)生新賽程并替換舊賽程，否則繼續(xù)使用舊賽程;

步驟8:轉(zhuǎn)步驟3;

2．2 聯(lián)盟競(jìng)賽算法的主要步驟

設(shè):L為參賽團(tuán)隊(duì)數(shù)量，S為最大比賽輪數(shù)，t為迭代輪數(shù)，n為團(tuán)隊(duì)的成員數(shù)(維數(shù))．Xti=(xti1，xti2，…，xtin)為團(tuán)隊(duì)i在第t輪比賽的團(tuán)隊(duì)陣型，f(Xti)為團(tuán)隊(duì)i在第t輪比賽的適應(yīng)值．主要步驟如下:

2．2．1 產(chǎn)生比賽賽程

常見(jiàn)的單循環(huán)賽制方法是逆時(shí)針輪轉(zhuǎn)法．設(shè)有8個(gè)團(tuán)隊(duì)，團(tuán)隊(duì)編號(hào)從1開(kāi)始．一個(gè)賽季有7輪比賽，賽程如下所示．(LCA允許在每個(gè)賽季后生成新賽程或繼續(xù)使用舊賽程)

2．2．2 判斷比賽輸贏

假設(shè)團(tuán)隊(duì)Xti和Xtj在第t輪比賽中是對(duì)手，適應(yīng)值分別是f(Xti)和f(Xtj)．令pti是團(tuán)隊(duì)i贏得這場(chǎng)比賽的概率，則pti滿足以下式子

若pti≥r0，則團(tuán)隊(duì)i贏、j輸;否則團(tuán)隊(duì)j贏、i輸．r0為［0，1］區(qū)間隨機(jī)數(shù)．

2．2．3 更新團(tuán)隊(duì)陣型

LCA使用SWTO分析法對(duì)團(tuán)隊(duì)陣型進(jìn)行更新，該方法包括內(nèi)部因素(優(yōu)勢(shì)或弱勢(shì))和外部因素(機(jī)會(huì)或威脅)．設(shè)第t輪比賽中，團(tuán)隊(duì)i和j是對(duì)手，團(tuán)隊(duì)l和k是對(duì)手;第t+1輪比賽，團(tuán)隊(duì)i和l是對(duì)手．使用sti和stl分別保存團(tuán)隊(duì)i和l在第t輪比賽的成績(jī)，值為1表示贏，－1表示輸．Xti=(xti1，xti2，…，xtin)的更新公式如下:

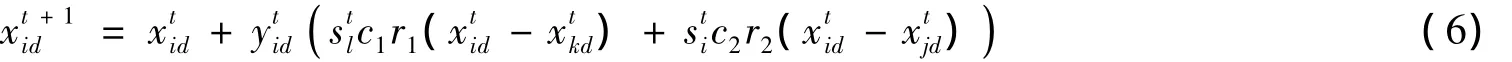
其中:d=1，…，n表示維數(shù);c1和c2是權(quán)重系數(shù);r1和r2是隨機(jī)數(shù);c1、c2、r1和r2∈［0，1］．ytid是二進(jìn)制數(shù)，為1表示允許第d維值更新，為0表示不允許更新．Yti=(yti1，yti2，…，ytin)為n維二進(jìn)制向量，qti用于控制團(tuán)隊(duì)i在第t輪比賽后團(tuán)隊(duì)隊(duì)員更新幅度，規(guī)定Yti集合中元素值之和為qti，即Yti中值為1的元素個(gè)數(shù)．式(6)第二項(xiàng)為外部因素，若stl為1(即團(tuán)隊(duì)k在上一輪比賽中輸了)則團(tuán)隊(duì)i往團(tuán)隊(duì)k的反方向發(fā)展，反之同理;第三項(xiàng)為內(nèi)部因素，若sti為1則團(tuán)隊(duì)i往團(tuán)隊(duì)j的反方向發(fā)展，反之同理．式中參數(shù)較多存在不合理性，但并非本文目的，期待后續(xù)論文對(duì)其改進(jìn)．LCA中使用截?cái)鄮缀畏植迹?］來(lái)定義qti的值，公式如下，其中r3是［0，1］區(qū)間的隨機(jī)數(shù)，pc∈(0，1)是輸入?yún)?shù)．

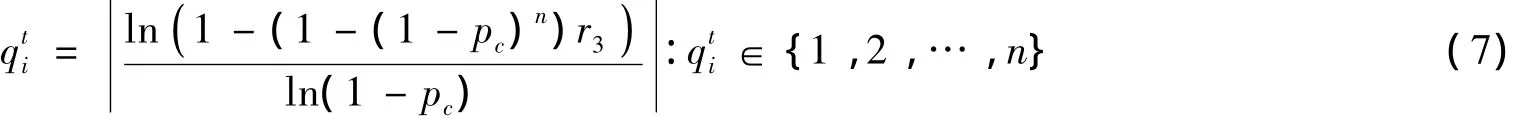
3 多目標(biāo)聯(lián)盟競(jìng)賽算法

Deb等提出的快速非支配排序遺傳算法NSGA－Ⅱ是近幾年來(lái)眾多多目標(biāo)進(jìn)化算法中較為優(yōu)秀和經(jīng)典的一個(gè)．因此本文的多目標(biāo)聯(lián)盟競(jìng)賽算法使用了該算法的框架，繼承了其優(yōu)點(diǎn)．在其算法框架基礎(chǔ)上，首先根據(jù)Pareto占優(yōu)機(jī)制重新定義了聯(lián)盟競(jìng)賽算法在團(tuán)隊(duì)陣型比賽輸贏上的判斷，并提出優(yōu)解擴(kuò)散策略改進(jìn)算法框架中生成子代群體的步驟，最后使用分布性指標(biāo)作為算法終止的依據(jù)．

3．1 算法基本流程

步驟1:初始化當(dāng)前(或父代)團(tuán)隊(duì)數(shù)量pop、當(dāng)前(或父代)團(tuán)隊(duì)陣型數(shù)組fatherpop、比賽輪數(shù)S等，令當(dāng)前迭代次數(shù)t=0，并產(chǎn)生比賽賽程;

步驟2:根據(jù)第t輪的比賽賽程進(jìn)行比賽，并按照一定規(guī)則判斷比賽輸贏;

步驟3:根據(jù)比賽結(jié)果產(chǎn)生子代團(tuán)隊(duì)群體數(shù)組childpop;

步驟4:將子代團(tuán)隊(duì)與當(dāng)前團(tuán)隊(duì)合并，并進(jìn)行快速非支配排序和擁擠距離計(jì)算［7］;

步驟5:按非支配等級(jí)和擁擠距離選擇pop個(gè)團(tuán)隊(duì)作為下一輪的父代種群，保存于fatherpop數(shù)組［7］;

步驟6:t=t+1，判斷是否滿足算法終止條件，若滿足轉(zhuǎn)步驟7，否則轉(zhuǎn)步驟2;

步驟7:將當(dāng)前所有團(tuán)隊(duì)作為最優(yōu)解集打印輸出．

其中步驟4和步驟5中的快速非支配排序、擁擠距離計(jì)算及選擇下一輪的父代種群均采用NSGA－Ⅱ算法中的方法．

3．2 團(tuán)隊(duì)輸贏判斷

與LCA不同，MOLCA是多目標(biāo)算法，因此團(tuán)隊(duì)輸贏的判斷需重新定義．本文根據(jù)Pareto占優(yōu)機(jī)制定義團(tuán)隊(duì)輸贏判斷規(guī)則，設(shè)x1，x2∈X，規(guī)則如下:

當(dāng)x1和x2無(wú)支配關(guān)系時(shí)，設(shè)兩者均為輸，以便于產(chǎn)生子代團(tuán)隊(duì)．

3．3 產(chǎn)生子代團(tuán)隊(duì)

首先引入優(yōu)解擴(kuò)散規(guī)模參數(shù)vscal，具體步驟如下:

步驟1:若本輪比賽結(jié)果全標(biāo)記為輸(全為平局)，且vcount＜vscal，轉(zhuǎn)步驟2，否則轉(zhuǎn)步驟3;

步驟2:根據(jù)優(yōu)解擴(kuò)散策略產(chǎn)生下一代群體;

步驟3:若vcount≥vscal，關(guān)閉優(yōu)解擴(kuò)散策略，且后續(xù)迭代中不能再采用優(yōu)解擴(kuò)散策略，轉(zhuǎn)步驟4;

步驟4:根據(jù)比賽結(jié)果每個(gè)個(gè)體均按式(6)產(chǎn)生一個(gè)子代個(gè)體，共產(chǎn)生規(guī)模為pop的子代團(tuán)隊(duì)群體．

其中vcount值為連續(xù)開(kāi)啟優(yōu)解擴(kuò)散策略的迭代次數(shù)，且每次在采取優(yōu)解擴(kuò)散策略前一輪迭代的fatherpop與采取優(yōu)解擴(kuò)散策略當(dāng)前輪的fatherpop有0．9×pop個(gè)個(gè)體的所有目標(biāo)值一樣．依據(jù)是，如果連續(xù)多次采用優(yōu)解擴(kuò)散策略，且每次群體的目標(biāo)值均無(wú)明顯變化，算法認(rèn)為群體基本收斂到Pareto前沿面．

優(yōu)解擴(kuò)散策略可理解為維多樣性搜索，目的是保證群體多樣性，防止在優(yōu)化多峰多目標(biāo)函數(shù)時(shí)陷入局部Pareto前沿面，matlab代碼如下:

(1)vi=1;

(2)for i=1:vscal

(3)for j=1:n

(4)vlen=(maxvalue(j)－minvalue(j))/(4*vscal);

(5)for k=1:vscal

(6) childpop(vi，:)=fatherpop(i，:);

(7) childpop(vi+1，:)=fatherpop(i，:);

(8) childpop(vi，j)=fatherpop(i，j)+vlen*k;

(9) childpop(vi+1，j)=fatherpop(i，j)－vlen*k;

(10) vi=vi+2;

(11)end

(12)end

(13)end

(14)childpop=region(childpop)．

其中:vi為子代種群下標(biāo)值，vlen為維搜索步長(zhǎng)，n為決策矢量維數(shù)，maxvalue(j)和minvalue(j)分別保存決策矢量第j維的決策上限和下限．

代碼第(2)行用于選取fatherpop的前vscal個(gè)團(tuán)隊(duì)個(gè)體;第(3)行遍歷每個(gè)個(gè)體的每一維;第(4)行是計(jì)算維搜索步長(zhǎng);第(5)行至第(11)行對(duì)每個(gè)個(gè)體的每一維以該維原來(lái)的值為基準(zhǔn)值以vlen為步長(zhǎng)分別遞增和遞減產(chǎn)生vscal個(gè)子代個(gè)體，共產(chǎn)生2×vscal個(gè)子代個(gè)體，覆蓋區(qū)間為2×vscal×vlen即占該維決策空間的一半;第(14)行用于限制childpop每個(gè)個(gè)體每維都在決策區(qū)間內(nèi)．優(yōu)解擴(kuò)散策略執(zhí)行一次將產(chǎn)生2×n×vscal2個(gè)子代團(tuán)隊(duì)，而vscal為常量，因此時(shí)間復(fù)雜度為O(n)．

優(yōu)解擴(kuò)散策略是針對(duì)優(yōu)化多峰多目標(biāo)函數(shù)，其有效性表現(xiàn)在抽取前vscal個(gè)個(gè)體遍歷其每維一半的決策空間，使原來(lái)的種群個(gè)體更加分散，因此不會(huì)帶來(lái)局部性;且該維的全局最優(yōu)值落在這一半決策空間內(nèi)的可能性較大，若該維陷入全局最優(yōu)區(qū)域，則其會(huì)將其它個(gè)體在該維上的決策值導(dǎo)向全局最優(yōu)值．因此每次使用優(yōu)解擴(kuò)散策略均會(huì)使每一維找到全局最優(yōu)值區(qū)域概率大大增加．

3．4 算法終止條件

首先介紹實(shí)驗(yàn)中采用的兩種多目標(biāo)優(yōu)化算法的評(píng)價(jià)指標(biāo)．收斂性指標(biāo)(convergence metric)和分布性指標(biāo)(spacing metric)．

收斂性指標(biāo):令P*=(p1，p2，…，p［P*］)為理想Pareto前沿面上均勻分布的Pareto最優(yōu)解集合，A=(a1，a2，…，a［A*］)是通過(guò)算法得到的近似Pareto最優(yōu)解集合．

收斂性指標(biāo)被定義為集合A中每個(gè)解ai距離P*的最小歸一化歐氏距離di的平均值，如式(9)所示，其中，fmaxm和fminm是集合P*中第m個(gè)目標(biāo)函數(shù)值的最大值和最小值．

分布性指標(biāo):令集合A是通過(guò)算法得到的近似Pareto最優(yōu)解集合．分布性指標(biāo)S定義如式(11)所示，

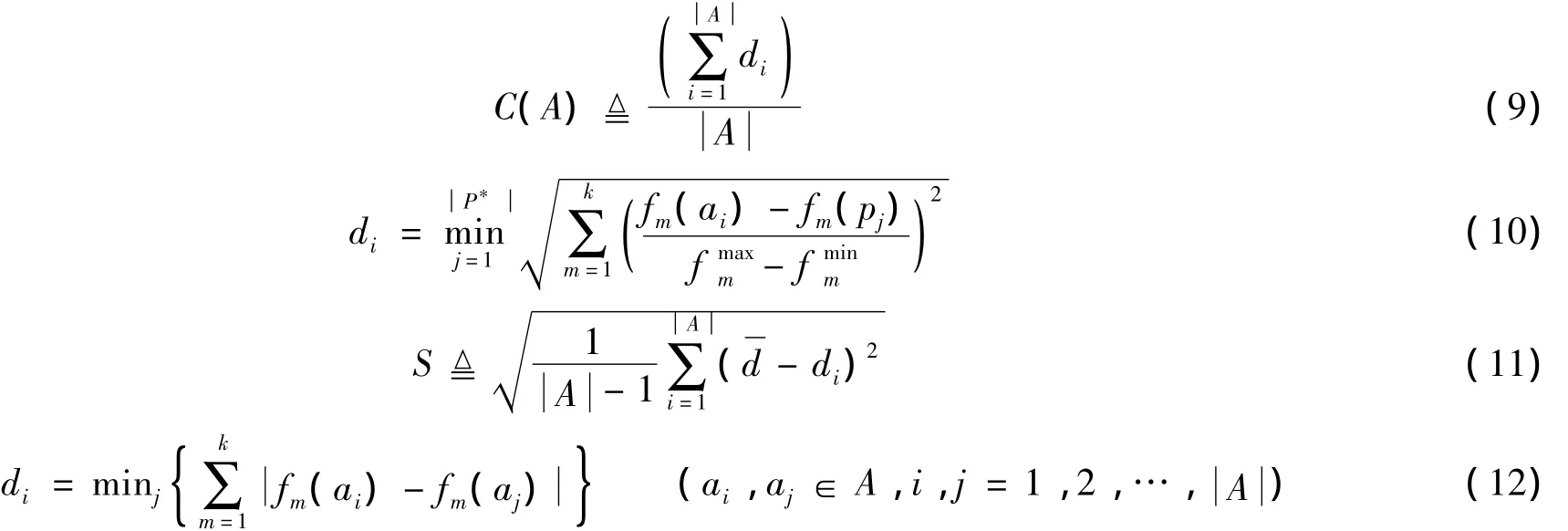
收斂性指標(biāo)越小意味著算法搜索到的近似Pareto最優(yōu)解集合越接近理想Pareto最優(yōu)解集合，分布性指標(biāo)越小意味著算法搜索到的近似Pareto最優(yōu)解集合分布越均勻．

MOLCA算法的終止條件定義為:當(dāng)前迭代輪數(shù)t≥S或者優(yōu)解擴(kuò)散策略已關(guān)閉且分布性指標(biāo)連續(xù)迭代2×vscal次無(wú)變小．

4 實(shí)驗(yàn)

選取NSGA－Ⅱ和MOEA/D算法作為比較算法對(duì)8個(gè)經(jīng)典多目標(biāo)函數(shù)進(jìn)行實(shí)驗(yàn)，函數(shù)相關(guān)數(shù)學(xué)描述如表1所示．實(shí)驗(yàn)中，三個(gè)算法均設(shè)置種群規(guī)模pop=200，優(yōu)化ZDT函數(shù)時(shí)最大迭代次數(shù)為250、優(yōu)化DTLZ函數(shù)時(shí)最大迭代次數(shù)為400．對(duì)MOLCA設(shè)置pc=0．1、c1=c2=1、vscal=5，對(duì)NSGA－Ⅱ設(shè)置交叉概率0．85，變異概率為0．01，對(duì)MOEA/D設(shè)置鄰居規(guī)模T=20．評(píng)價(jià)指標(biāo)有收斂性指標(biāo)、分布性指標(biāo)和函數(shù)評(píng)價(jià)次數(shù)．其中函數(shù)評(píng)價(jià)次數(shù)常作為算法終止條件，與最大迭代次數(shù)類(lèi)似．三個(gè)算法均對(duì)每個(gè)測(cè)試函數(shù)獨(dú)立運(yùn)行30次，實(shí)驗(yàn)結(jié)果如圖1、圖2和表2所示．圖1是算法平均收斂性指標(biāo)實(shí)驗(yàn)結(jié)果，圖2是算法平均分布性指標(biāo)實(shí)驗(yàn)結(jié)果，表2是函數(shù)評(píng)價(jià)次數(shù)實(shí)驗(yàn)結(jié)果，由于MOEA/D和NSGA－Ⅱ算法在獨(dú)立運(yùn)行的30次實(shí)驗(yàn)中都是迭代到固定輪數(shù)后算法才終止，其中測(cè)試ZDT時(shí)為250輪，即函數(shù)評(píng)價(jià)次數(shù)為250×pop=50 000，而測(cè)試DTLZ時(shí)為400輪，即函數(shù)評(píng)價(jià)次數(shù)為400×pop=80 000．

表1 測(cè)試函數(shù)的相關(guān)描述Tab．1 The relevant description of test functions

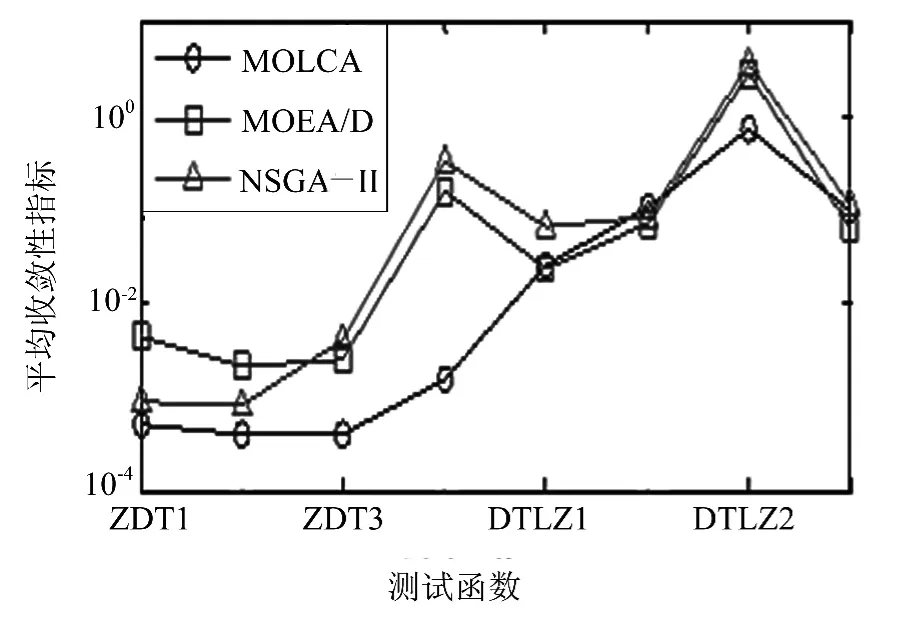
圖1 三種算法的收斂性指標(biāo)Fig．1 The convergence metric of the three algorithms

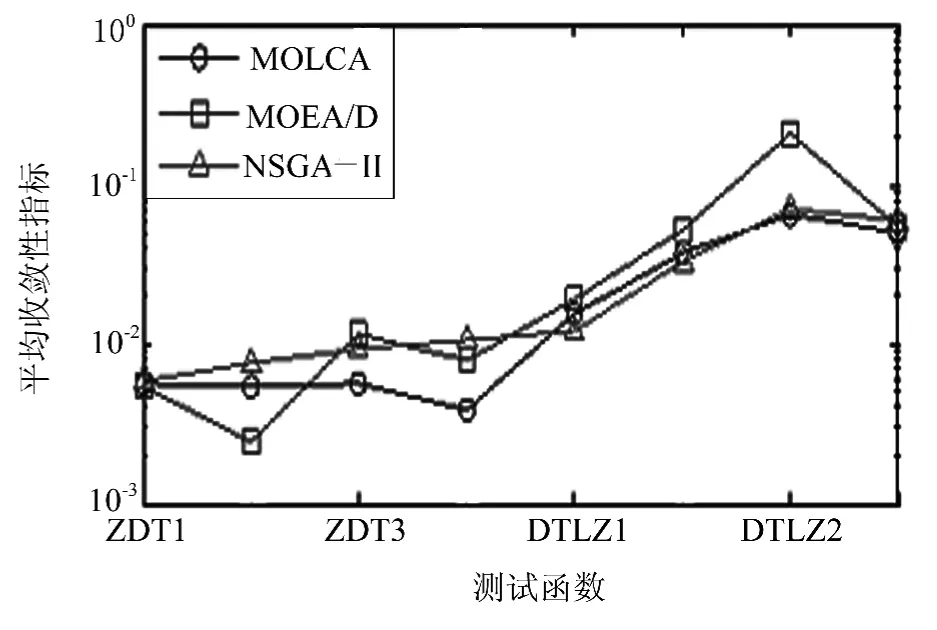
圖2 三種算法的分布性指標(biāo)Fig．2 The spacing metric of the three algorithms

表2 三種算法的函數(shù)評(píng)價(jià)次數(shù)Tab．2 The number of evaluations of three algorithms

從圖1收斂性指標(biāo)可以看出，對(duì)于優(yōu)化ZDT1、ZDT2、ZDT3、ZDT4和DTLZ3測(cè)試函數(shù)時(shí)，MOLCA算法較MOEA/D和NSGA－Ⅱ均有明顯優(yōu)勢(shì);對(duì)于優(yōu)化DTLZ1和DTLZ4測(cè)試函數(shù)時(shí)，MOLCA稍劣于MOEA/D，但仍優(yōu)于NSGA－Ⅱ;對(duì)于優(yōu)化DTLZ2測(cè)試函數(shù)時(shí)，MOLCA稍劣于MOEA/D和NSGA－Ⅱ．從圖2可以看出，對(duì)于優(yōu)化ZDT3和ZDT4測(cè)試函數(shù)時(shí)，MOLCA的分布性指標(biāo)較其它算法有優(yōu)勢(shì);對(duì)于優(yōu)化DTLZ2和DTLZ3函數(shù)函數(shù)時(shí)，MOLCA的分布性指標(biāo)與NSGA－Ⅱ相當(dāng)，優(yōu)于MOEA/D;對(duì)于優(yōu)化ZDT1、DTLZ1和DTLZ4，三個(gè)算法的分布性指標(biāo)均相差無(wú)幾;僅在優(yōu)于ZDT2函數(shù)函數(shù)時(shí)，MOLCA的分布性指標(biāo)稍差于MOEA/D．從表2可以看出，除優(yōu)化ZDT4和DTLZ2測(cè)試函數(shù)時(shí)，函數(shù)評(píng)價(jià)次數(shù)略多于其它算法之外，優(yōu)化其余測(cè)試函數(shù)時(shí)，函數(shù)評(píng)價(jià)次數(shù)均明顯少于其它算法．

綜上分析，多目標(biāo)聯(lián)盟競(jìng)賽算法在優(yōu)化大部分多目標(biāo)測(cè)試函數(shù)時(shí)，在不失解的分布均勻性情況下且使用更少的函數(shù)評(píng)價(jià)次數(shù)依然能獲得比MOEA/D和NSGA－Ⅱ更加接近于真實(shí)Pareto前沿面的解集，因此認(rèn)為多目標(biāo)聯(lián)盟競(jìng)賽算法是可行的和有效的．

5 結(jié)論

將聯(lián)盟競(jìng)賽算法擴(kuò)展為多目標(biāo)聯(lián)盟競(jìng)賽算法，根據(jù)Pareto支配關(guān)系重新定義團(tuán)隊(duì)陣型比賽輸贏的判斷，并在算法中加入優(yōu)解擴(kuò)散策略使算法不輕易陷入局部最優(yōu)解，最后結(jié)合優(yōu)解擴(kuò)散開(kāi)關(guān)和分布性指標(biāo)使算法自動(dòng)停止運(yùn)行．通過(guò)對(duì)8個(gè)ZDT和DTLZ測(cè)試函數(shù)的實(shí)驗(yàn)及MOEA/D算法和NSGA－Ⅱ算法的對(duì)比分析，驗(yàn)證了新算法具有優(yōu)良的解搜索能力．