具有非線性等式約束的故障診斷集員濾波器設計

阮玉鎮，苗琳璐，王 武

(1．福建工程學院機械與汽車工程學院，福建福州 350118;2．福州大學電氣工程與自動化學院，福建福州 350116)

0 引言

在控制界和信號處理界，故障診斷是動態系統的基本問題之一．因此，自1971年故障診斷技術產生以來，其研究得到了越來越多學者的青睞，目前依然是研究熱點之一［1－3］．在一些實際應用系統，如化學處理過程［4］、目標跟蹤［5］、投資問題［6］，其噪聲分布未知但有界，且希望系統的狀態能100%估計出．基于隨機噪聲的卡爾曼濾波方法［7］要求噪聲分布已知，對系統狀態的估計是點估計，無法估計出100%包含系統狀態的界，因此無法勝任此類情況．集員濾波就是針對這類情況出現的一種濾波方法，它僅要求噪聲約束界就能夠保證被估計狀態值在設計要求的范圍內．基于這些優點，其應用涉及到很多領域，如電力系統［8］、機器人系統［9］、非線性系統［10］等．

針對實際工程中有狀態約束的控制系統，許多學者提出研究狀態約束問題的方法［11］．投影法是狀態約束處理方法中研究最多、最普遍的一種方法，它的基本思想是首先獲得一個沒有約束的解決方案，然后將無約束的狀態投影到有約束的狀態約束表面，該方法克服了數值和空間問題，具有較強的可實現性，因此較多的文獻都是采用投影法．

綜上所述，針對具有狀態約束的動態系統，采用投影法處理狀態約束，選擇集員濾波方法用于故障診斷，所設計的濾波器不僅能有效檢測出故障，保證系統狀態、故障在一定范圍內，并且能判定出故障類型．

1 問題描述

考慮如下線性時變系統:

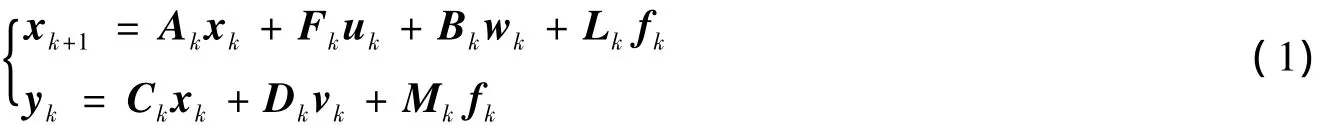
其中:xk∈Rn為系統狀態，uk∈Rnu為已知輸入，yk∈Rny為測量輸出，Ak，Bk，Ck，Dk，Fk，Mk和Lk為已知的時變矩陣，wk∈Rnw為過程噪聲，vk∈Rnv為測量噪聲，fk∈Rnf為故障信號，分別屬于超橢球集合:

其中:Qk=QTk＞0，Rk=RTk＞0和Sk=STk＞0為已知矩陣．系統的初始狀態x0，f0滿足超橢球集合約束:

其中:h(·)為非線性函數;dk為已知常數．

對于系統(1)，設計集員濾波器:

設計目標是對任意時刻k+1，具有非線性等式約束(4)的系統(1)，在給定過程噪聲wk、觀測噪聲vk和故障信號fk有界的情況下，設計集員濾波器(5)，保證系統狀態、故障信號100% 在超橢球界內，即系統狀態、故障信號滿足以下性能指標:

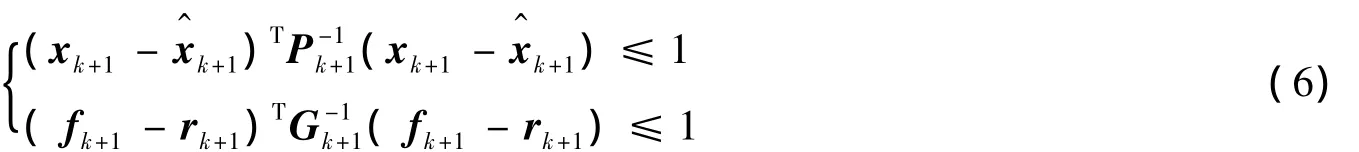
2 主要結果

定理1 針對具有非線性等式約束(4)的系統(1)，在任意k+1時刻，給定測量輸出yk+1，如果:

1)過程噪聲wk∈Wk、觀測噪聲vk∈Vk和故障信號fk∈Ψk;

2)xk和fk滿足:(xk－)TP－1k(xk－)≤1，(fk－rk)TG－1k(fk－rk)≤1，其中，rk，Pk和Gk已知;

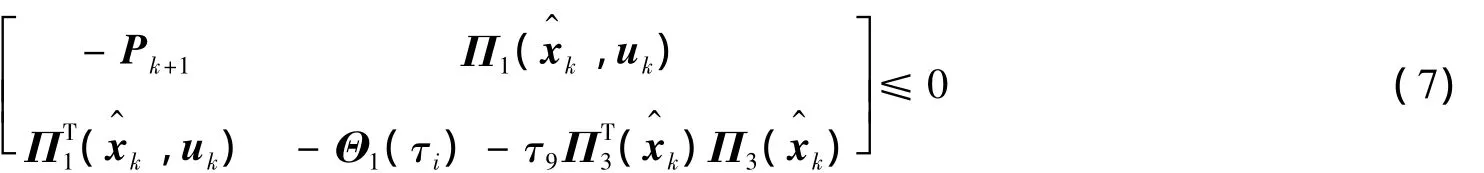
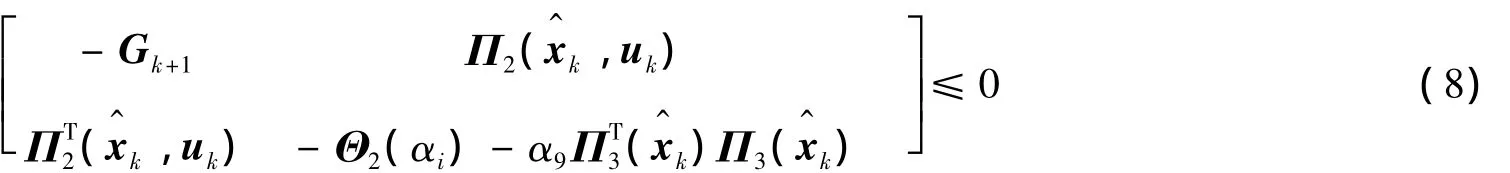
其中:

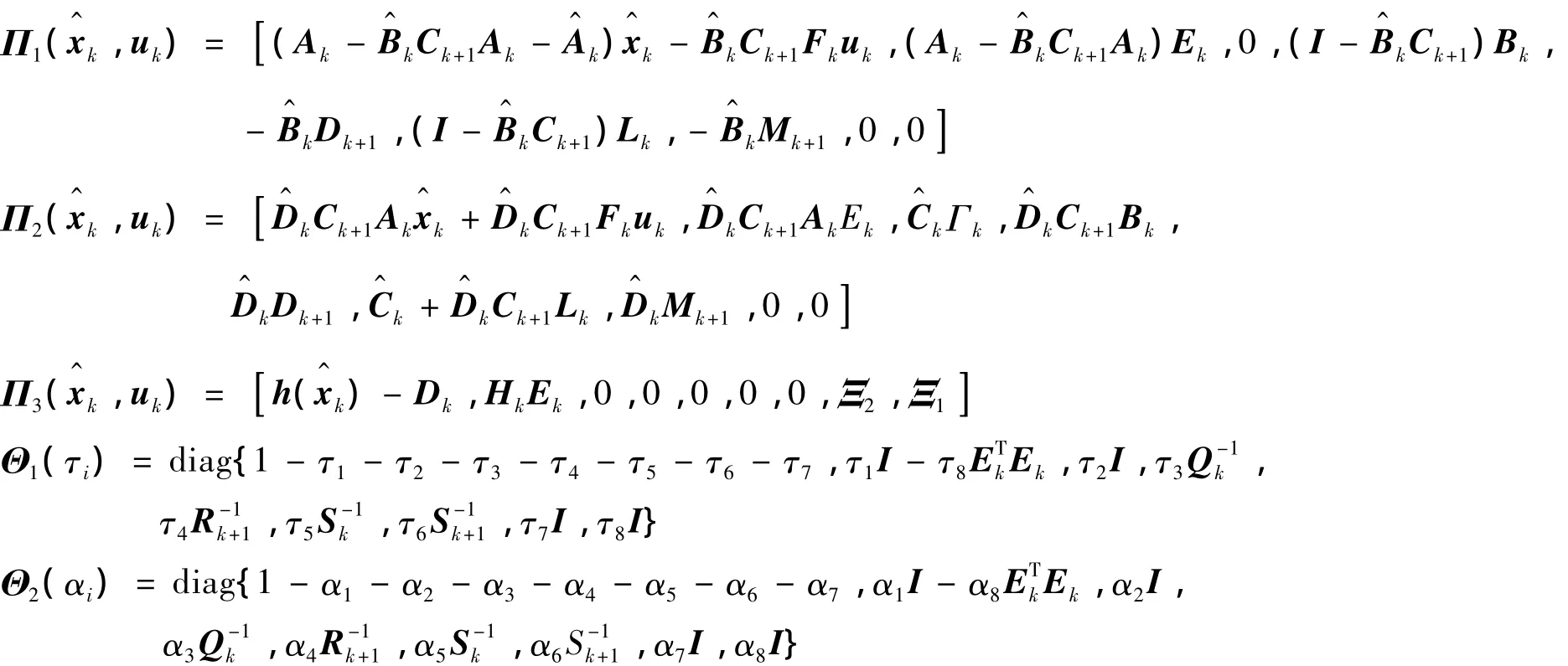
那么:①系統存在集員濾波器(5);②xk+1和fk+1滿足式(6)，即保證系統的狀態、故障信號100%包含在超橢球界內．

證明 假設在第k步時，系統狀態xk和故障fk滿足:

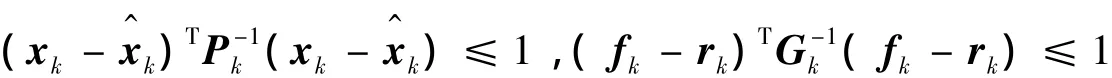
那么?z，?s滿足 z≤1， s≤1，且存在矩陣Ek和Γk滿足Pk=EkETk和Gk= ΓkΓTk，上述約束條件可轉化為:

那么在k+1時，由式(5)和式(9)可得狀態估計誤差和故障估計誤差分別為:

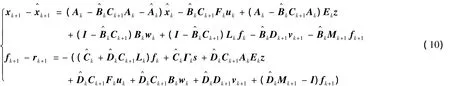
對非線性等式約束進行線性化，式(4)可寫為

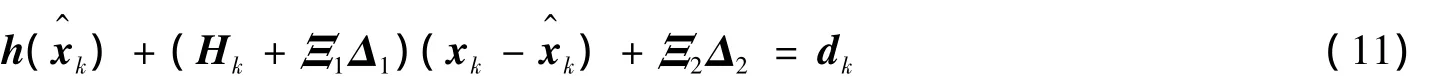
式中:Hk為雅克比矩陣;Ξ1和Ξ2是已知的標量矩陣;Δ1和Δ2是未知但有界的矩陣，且 Δ1≤1， Δ2≤1;Ξ1Δ1代表線性化過程基準點誤差;Ξ2Δ2代表泰勒展開時高階截斷誤差．代入式(9)，式(11)為:

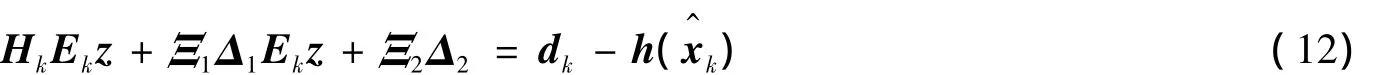
令Δ3=Δ1Ekz，那么式(12)為:

定義向量η為:

由式(10)，式(6)可寫為:

同理，式(13)可寫為:

已知向量 z，s，wk，vk+1，fk，fk+1，Δ2和 Δ3滿足:

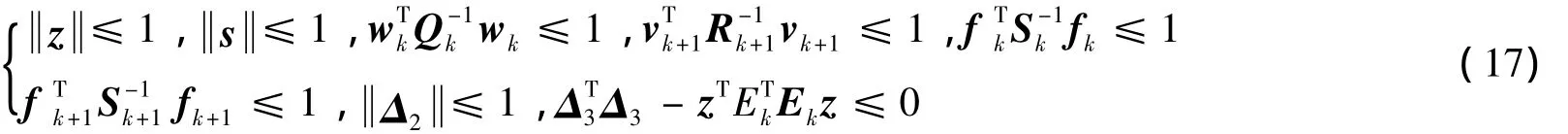
將式(17)寫成向量η的不等式形式，連同式(15)應用S－procedure引理，可得存在τi＞0，αi＞0，i=1～8使得式(18)成立．

由式(16)和式(18)應用Finsler引理可得:

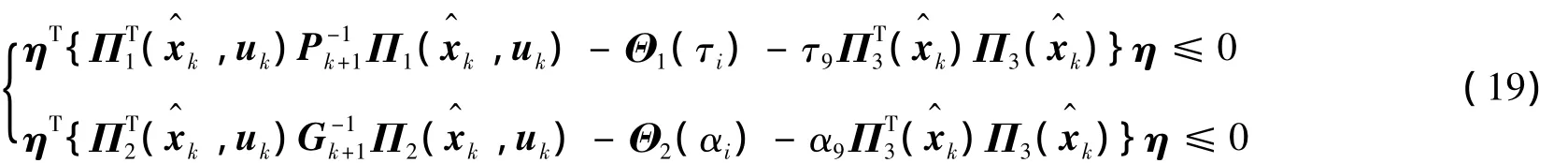
由Schur補引理可知，如果式(7)和式(8)成立，那么式(19)成立，即存在一個形如式(5)的集員濾波器，使得xk+1和fk+1滿足式(6)．證畢．

注1 定理1給出了存在集員濾波器的LMI條件和集員濾波器參數設計方法．利用Matlab LMI Toolbox，解決如下凸優化問題，就可得到集員濾波器參數．

注2 根據文獻［12］中給出的故障判別方法來進行故障檢測．故障檢測時，選取評價函數為:

其中:k0為初始評價時刻;L為評價步數．由于故障常常發生在有限時間段內，所以L是有限值．閾值的選取必須要考慮外界干擾的影響，為了盡量避免沒有故障信號時出現誤檢測，而有故障信號時又要盡量迅速地檢測出故障，取閾值函數為:

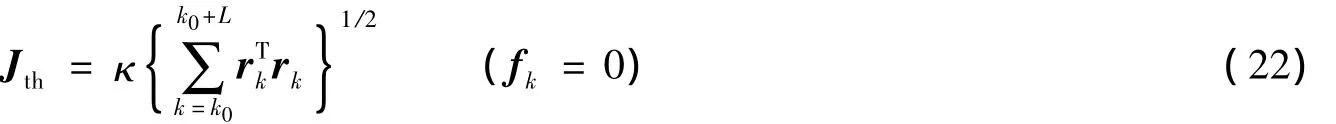
其中κ為閾值系數．通過計算每一時刻J(rk)和Jth的值來檢測故障是否發生，即

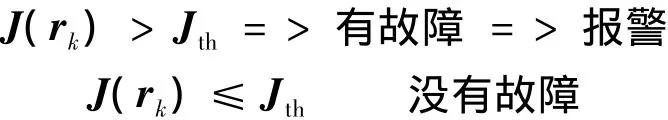
3 仿真研究

系統(1)參數如下:

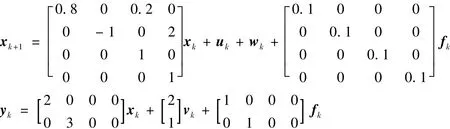
其中:xk= ［xk1xk2xk3xk4］T，fk= ［fk1fk2］T．非線性狀態約束為:(ζ+xk1)2+x2k2=ζ2

利用Matlab LMI Toolbox對優化問題(20)進行尋優，首先，假設同一時刻只有一個部件發生故障:

1)fk1，fk2，fk3和fk4取同種故障，且為正弦信號:

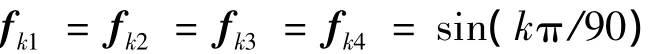
2)fk1，fk2，fk3和fk4取同種故障，且為方波信號:

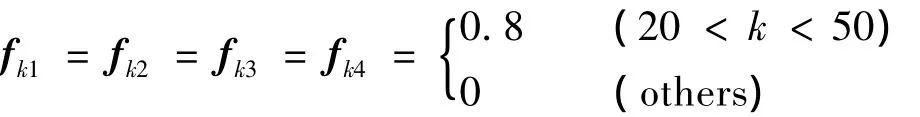
圖1和圖2給出了在1)、2)故障情形下，狀態變量xk1和xk2的真實值、估計值、上界線、下界線比較，無論故障為何種形式，只要故障信號的值有界，狀態變量xk1和xk2100%在上下界內，滿足性能要求．圖3和圖4分別是故障形式為1)、2)時的rk1估計值、上下界與真實值fk1比較圖，圖3和圖4表明故障信號的估計值100%在上下界內，也滿足性能要求，從故障波形圖還可以判斷出故障類型．

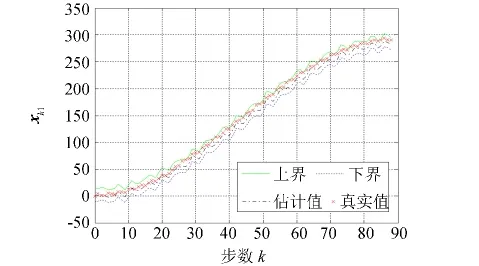
圖1 x k1真實值、估計值、上下界Fig．1 The upper bound，the lower bound，the estimate and the true value of x k1

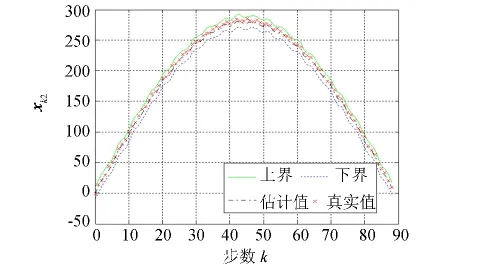
圖2 x k2真實值、估計值、上下界Fig．2 The upper bound，the lower bound，the estimate and the true value of x k2

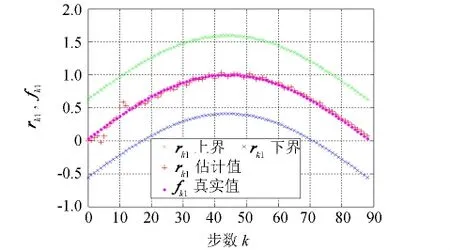
圖3 故障為情形1)時，r k1與f k1Fig．3 Under the fault of case 1，the true value of f k1 and the estimate value of r k1

圖4 故障為情形2)時，r k1與f k1Fig．4 Under the fault of case 2，the true value of f k1 and the estimate value of r k1

k2k1k2k1取κ=1．2，根據式(21)和式(22)計算每一時刻的殘差評價函數值J(r)和閾值Jth，判斷二者數值就可以檢測出故障．通過仿真得到當k=24時，J(rk)=0．653 42＞Jth=0．144，說明故障在出現后第24步就可以被檢測出來，如圖6所示．

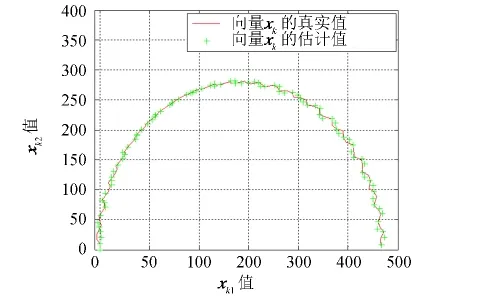
圖5 x k1/x k2真實值與估計值Fig．5 The true and the estimate value of x k1/x k2

圖6 故障為情形2)時，J(r k)和J thFig．6 The value of J(r k)and J thunder the fault of case 2

4 結論

針對具有非線性等式約束的線性時變系統提出了一種集員濾波器的設計方法，該方法保證系統狀態、故障100%包含在上下界內．對非線性約束進行線性化并采用S－過程和Finsler引理得到集員濾波器存在凸條件，運用LMI方法就可求解所設計的集員濾波器參數．數值仿真表明，所設計的集員濾波器能100%估計出系統狀態和故障的界，而且還能夠辨別出故障類型，及時檢測出故障．