一種基于遺傳算法的進路搜索算法

張文泉 余立建

在鐵路車站作業中，進路選排對接發車作業的效率和車站通過能力有著直接影響，如何高速有效地選排接發列車和調車作業進路，是保證行車安全和提高行車效率的重要內容。

在計算機聯鎖的進路選排中，進路搜索的方法有很多種。最常見的有鏈表法、二叉樹搜索法等。近年來智能優化算法在求解路徑優化等問題方面顯示了較強的優勢，所以也可以采用智能算法來進行進路搜索。本文就提出了一種基于遺 傳 算 法 （genetic algorithm，簡稱GA）的進路搜索算法，這種方法以遺傳算法為核心，具有快速、準確的特點，能夠有效地進行進路搜索。

1 站場數據結構分析

為了簡化建模過程，本文只考慮列車進路選排，暫不考慮調車進路選排，下面以 《6502電氣集中電路》中的一個典型站場簡化圖為例進行分析和建模。如圖1所示。

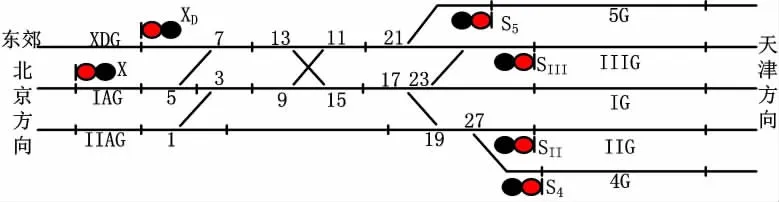
圖1 站場平面圖

首先需要簡化站場圖，將站場圖以節點的形式進行描述。因進路選排過程中，主要需要考慮信號機、軌道區段和道岔，將信號機、軌道區段以及道岔都作為站場圖節點，并進行統一定義。對于圖1所示站場，按照由下向上、由左向右的順序對節點依次進行奇數編號。由于信號機、道岔以及軌道區段在位置上可能重復，所以為了避免重復定義節點，在定義過程中先選擇道岔作為節點，再選擇軌道區段，最后再考慮信號機。對于一條進路，各個節點的前后連接關系十分重要，所以采用數據結構圖表示整個站場，圖1站場的數據結構圖如圖2所示。

圖2中，k1，k3…均表示當前節點的編號；pf1表示水平方向上所連接的前一節點的編號，pf2表示渡線方向上所連接的前一節點的編號，若不存在則賦值為0。

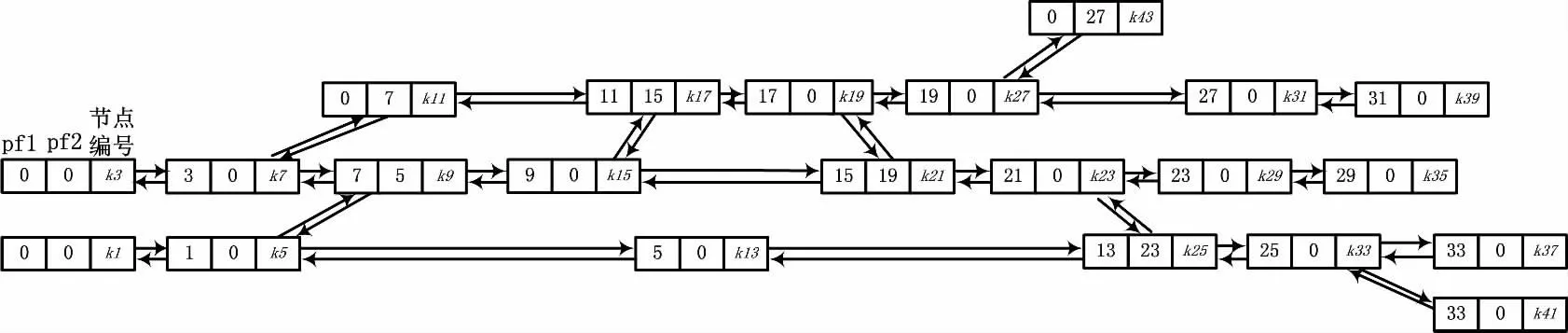
圖2 數據結構圖

2 進路搜索的遺傳算法建模

2．1 編碼與染色體

根據節點取值特點，選取二進制編碼。在遺傳算法中，一條特定的進路可以表示成一條染色體，將一組染色體放入到問題環境中，通過適者生存的規則選擇出適合環境的個體進行遺傳。Ki表示一條特定的進路，即是一條染色體，Ki＝ ｛ki1，ki2，…kin｝。

當站場數據結構圖確定后，節點數也就隨之確定。在進路選排過程中，如果讓節點ki為1表示選中、為0表示未選中，則 ｛k1，k2，…kn｝就可以表示一條搜索出的進路。于是進路搜索的問題就可以抽象成在眾多的解Ki＝｛ki1，ki2，…kin｝中選擇最優解的問題。

2．2 進路搜索的遺傳操作

設K為進路搜索的集合，算法初始狀態的進路搜索集合作為初始種群，在大小為m的初始種群中，Ki表示第i個染色體。遺傳算法的基本流程見圖3。

在整個遺傳算法過程中，主要進行三個遺傳操作，分別是復制操作 （選擇）、交叉操作和變異操作。復制操作是根據每個個體的適應度大小進行優勝劣汰，將適應度更高的遺傳到下一代。本文采用輪盤賭的方法，即將所有個體的適應度求和作為分母，每個個體自身的適應度作為分子，按比例進行選擇。因此，每個個體被選擇的概率為

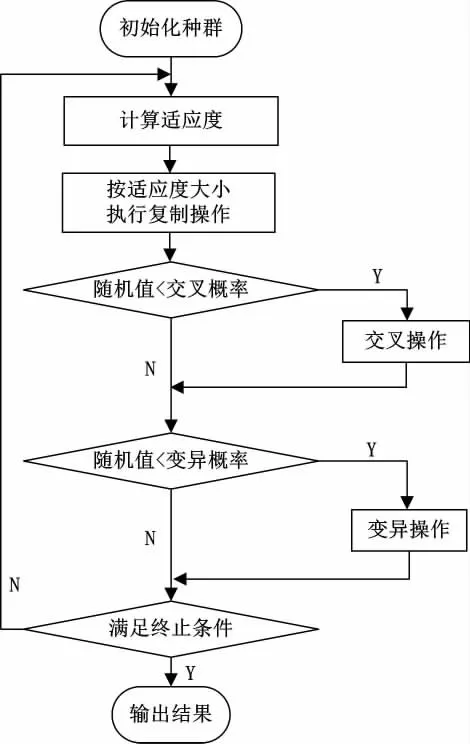
圖3 遺傳算法流程圖

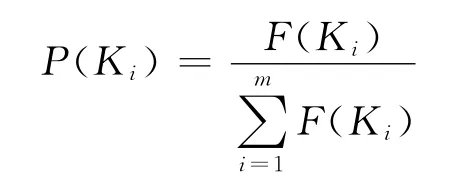
交叉操作是選擇父代中2個個體，將這2個個體的某一段進行交換得到新的2個個體，本文采用單點交叉。變異操作是對單個個體進行的操作，在單個個體的某個基因上按照某個較小的概率進行取反操作，使之產生新的個體，從而改善進路搜索能力。

2．3 適應度函數

一個個體若能夠構成一條合理的進路，則從始端節點到終端節點需依次相連。即一個個體中去除為0的信息后組成新的子集，該子集所包含的節點應連續。此時，各個節點的節點編號并不發生變化，用一個新的數組n表示。例如，某個個體K為 ｛0 1 0 1 1 0 0 1 0 0 1 1 0 0 1 0 0 1 0 0 0 0｝，對應的節點編號為 ｛1，3，5，…41，43｝，個體K去除0信息后組成新的子集 K′ 為 ｛1 1 1 1 1 1 1 1｝，對應的節點編號為 ｛3，7，9，15，21，23，29，35｝，記作數組n。

另外，同一組始端和終端節點之間可能存在著多條進路，因此還需要處理多余的變更進路。根據如上分析，確定了優化目標為

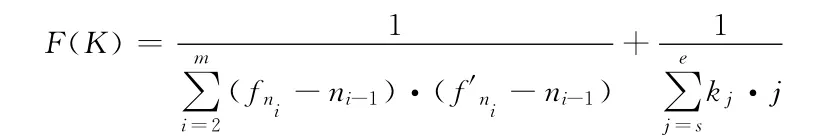
其中，fni表示節點kni的pf1值，f′ni表示節點kni的pf2值，ni表示個體去除0信息后組成子集的節點編號；m表示子集長度；kj表示節點取值，j表示節點編號；s表示始端節點編號；e表示終端節點編號。上式中的第一項表示能否構成合理進路，第二項表示去除多余變更進路。

3 進路搜索模型改進

雖然建立了基于遺傳算法的進路搜索模型，但是要將這種模型應用到實際的進路選排過程中，還需要考慮信號燈的變化以及道岔的轉動。因此，必須對上述的基本模型進行改進。

首先在一個站場中，每一架列車信號燈均對應一個股道區段，以圖1站場圖為例就有如表1所示的對應關系。

因此，當該股道區段所對應節點為始端節點時，則該股道區段所對應的列車信號機由紅燈狀態變為綠燈狀態，即信號開放。其次，當選定節點時，相應節點所對應的道岔需要進行動作。為了便于道岔動作的判斷，對前面的數據結構進行改進，加入一項新的數據L，即節點所在的股道編號，如圖4所示。

圖4 改進的單節點數據結構

其中，L（k3）＝0，即節點k3所在的股道編號為0。在整個站場中，L（i）表示節點ki所在股道的編號。在搜索到一條進路以后，進路中所有節點的前后節點隨之確定。此時，若L（i）≠L（i－1）或者L（i）≠L（i＋1），則節點ki所對應的道岔需要轉動。

表1 股道與信號燈對應關系

4 實例仿真分析

以圖1站場為例，可以選擇任意一條列車進路進行選排。下面以北京方向下行至5G接車進路的選排為例進行仿真分析。

步驟1：依次按下始端按鈕 （XJA）和終端按鈕 （S5LA）。此時，對應的進路搜索起始節點和終止節點被確定，分別是k3和k43，參見圖2。

步驟2：利用遺傳算法搜索列車進路。遺傳算法參數分別為，群體規模取80，交叉概率pc取0．6，突變概率pm取0．1。仿真結果如圖5所示。

顯然，在迭代32次以后適應度F達到最大值且不再變化，此時F＝1．0149。得到的最優個體為 ｛0 1 0 1 0 1 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 1｝，對應的最優進路節點為k3－k7－k11－k17－k19－k27－k43。經多次試驗表明，遺傳算法的初始種群均隨機產生，收斂速度也隨之變化，但均能在一定的迭代次數后收斂。

步驟3：相應道岔的轉動。根據數據結構可知，搜索到的節點確定以后，相對應道岔關系也隨之確定，如表2所示。

步驟4：開放信號燈。信號燈的開放和始端按鈕 （或起始節點）所在股道區段相關，由于此時的搜索起始節點k3所對應的股道區段是IAG，由表1可知，需開放信號燈X。

至此，整個進路選排完畢，X信號機開放。

值得注意的是在遺傳算法的計算過程中，有時會陷入局部最優從而影響最終結果，為了避免這種情況的發生，可以對遺傳算法進行改進。同時也可以采用冗余計算的方法，比較選取最優結果，防止局部最優解的出現。

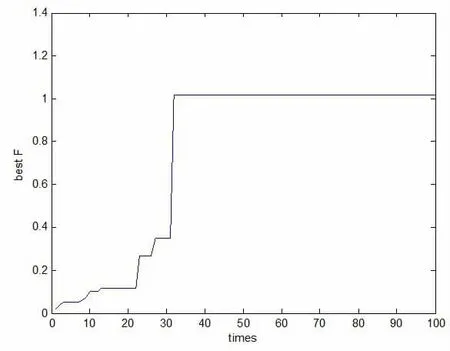
圖5 遺傳算法仿真結果

5 總結

通過對站場圖進行數據結構分析，在此基礎上提出了一種基于遺傳算法模型的進路選排算法。通過仿真證明，這種進路選排算法可以簡單便捷的搜索出一條合理的進路，是一種具有可行性的進路選排算法。

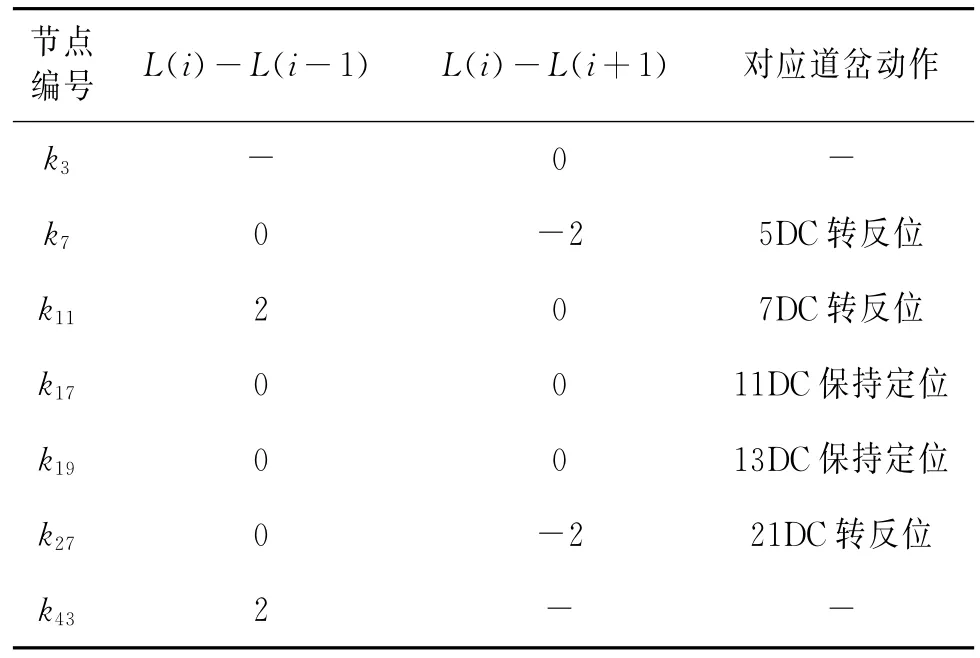
表2 道岔轉動關系

［1］ 何文卿．6502電氣集中電路［M］．北京：中國鐵道出版社，2011．

［2］ 陳志穎，董昱，楊柳，李亮．計算機聯鎖進路搜索算法的分析與研究［J］．鐵路通信信號，2007．4，43（4）：4．

［3］ 陳榮武，劉莉，郭進．基于遺傳算法的列車運行能耗優化算法［J］．交通運輸工程學報，2012．2，12（1）：111－112．