基于PMU/SCADA混合量測狀態估計及不良數據檢測方法

許　勇

(西南交通大學電氣工程學院,四川 成都　610031)

基于PMU/SCADA混合量測狀態估計及不良數據檢測方法

許勇

(西南交通大學電氣工程學院,四川 成都610031)

摘要：充分利用PMU量測及SCADA量測值，討論并發展了一種基于PMU/SCADA混合量測的電力系統狀態估計及不良數據檢測方法。首先利用快速分解狀態估計得到估計結果，再將狀態估計結果和PMU量測值進行二次線性狀態估計。同時利用二次線性狀態估計更新殘差協方差矩陣的方式來對SCADA量測量中的關鍵量測量是否存在不良數據進行檢測。最后采用IEEE 30節點系統驗證了該方法的有效性。

關鍵詞：電力系統；相量測量單元；混合狀態估計；不良數據檢測

0引言

電力系統狀態估計(state estimator)是電力調度中心能量管理系統(energy management system,EMS)非常重要的組成部分，更是電網安全評估、預防控制和運行分析等各種高級應用的基礎[1]。其基本原理是根據量測數據的冗余度，按照最佳估計準則對生數據進行相關處理，使得量測數據更好的接近真實值。

近年來，同步相量測量單元(phasor measurement unit,PMU)相對于數據監控及采集系統(SCADA)能對測量節點提供更高精度的相量測量。但是PMU量測裝置成本較高，不能在短時間內將SCADA完全取代，這將會與SCADA長期共存[2]，因此，將SCADA和PMU量測相結合進行混合狀態估計是一種比較理想的方法。目前相關研究已經取得了一定的成果[3-6]，文獻[7]提出了二次狀態估計的思想，這對提高狀態估計的精度有明顯提高，但是耗時較長，通過對非線性狀態估計進行優化的方法，這樣既可以提高狀態估計的精度、縮短估計運行時間，又能很好地滿足電力系統實時性的要求。

評價一種狀態估計算法是否優良，不僅要保證該算法能夠高效快速地估計出電力系統中狀態量的值，同時具備一定的不良數據處理能力，以確保狀態估計結果的準確性。首先對混合量測電力系統狀態估計算法進一步探討，并提出了一種對SCADA量測量中的關鍵量測量出現不良數據的檢測方法，最后，通過實驗驗證了該方法的有效性。

1混合量測線性狀態估計算法

1.1　非線性狀態估計模型

快速解耦狀態估計算法是將加權最小二乘法進行了改進，其量測量是通過SCADA獲取，其數學模型為

(1)

式中：Za和Zr分別為電壓幅值和電壓相角的量測數據；υa和υr分別為電壓幅值和電壓相角的量測誤差。

由于在電網中電壓幅值U主要受無功功率Q的影響，節點相角θ主要受有功功率P的影響，因此，Za主要是支路有功功率或有功注入量測量，Zr主要是支路無功功率或無功注入量測量。

同樣地，雅可比矩陣可改寫為

(2)

同時，權值矩陣也可以分解為有功和無功兩部分，即

(3)

由于節點電壓幅值主要受無功功率影響，節點電壓相角主要受有功功率影響，式(2)中Har≈0及Hra≈0。于是信息矩陣可以寫成

(4)

由于信息矩陣一般為稀疏矩陣，由潮流計算可得

(5)

將式(4)帶入式(5)右端，可得迭代修正方程為

AΔθ(l)=a(l)

BΔu(l)=b(l)

(6)

式中：

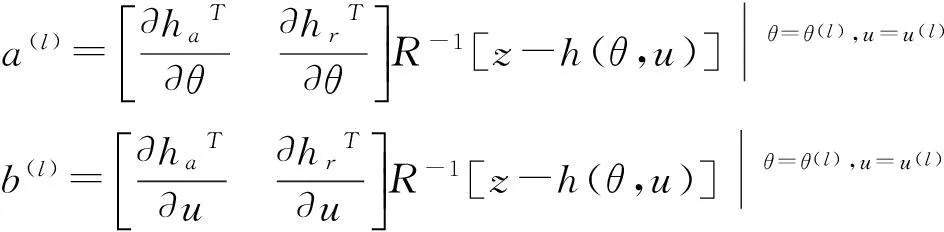
(7)

1.2　線性狀態估計模型的建立

將電力系統各節點和支路的實部電流和虛部電流及快速解耦狀態估計結果用直角坐標的各節點電壓向量表示，然后可以得到電力系統線性量測方程組，其數學模型為

(8)

由于雅可比矩陣高度稀疏，且與系統拓撲及參數無關，從而大大簡化了線性狀態估計的計算量。對于上面的量測方程，由加權最小二乘原理可以求得線性狀態估計計算式為

(9)

(10)

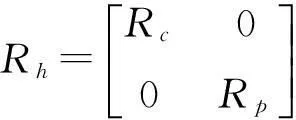
2不良數據檢測

當系統量測冗余度較低時，系統中可能存在關鍵量測量，而關鍵量測量不是一個冗余量測量。如果將關鍵量測量從量測系統中刪除，將導致系統不可觀測，因此，利用PMU量測信息來提高整個系統的量測冗余度并對SCADA量測中關鍵量測量出現不良數據時進行檢測。檢測的基本公式為

(11)

式中：

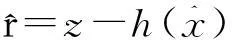
(12)

D=cov(r)=R-H(HTR-1H)-1HT

(13)

1) 非關鍵量測量的不良數據檢測

(14)

Dc=cov(r)=Rc-Hc(HcTRc-1Hc)-1HcT

(15)

式中：Rc和Hc分別是來自傳統狀態估計的量測誤差的協方差矩陣和雅克比矩陣。

2) 關鍵量測量的不良數據檢測

(16)

D=cov(r)

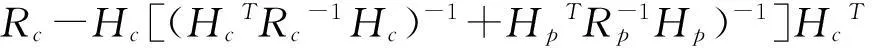
(17)

式中：Rp和Hp分別是混合量測狀態估計的量測誤差的協方差矩陣和雅克比矩陣。

3算例分析

采用IEEE 30節點系統對該算法進行算例分析。PMU裝置裝設位置為8、9、12、24、25節點，如圖1所示。仿真軟件選用Matlab 7.0。其中，SCADA量測值和PMU量測值都是在潮流計算結果的基礎上分別疊加10-2和10-4的正態分布隨機量測誤差，沒有加入PMU量測量之前，整個SCADA量測系統是完全可觀測的，并且冗余度的比例保持在1.1到1.3之間。所有的檢測情況都將檢測的閾值設置為2.81(99.5%的置信度)。

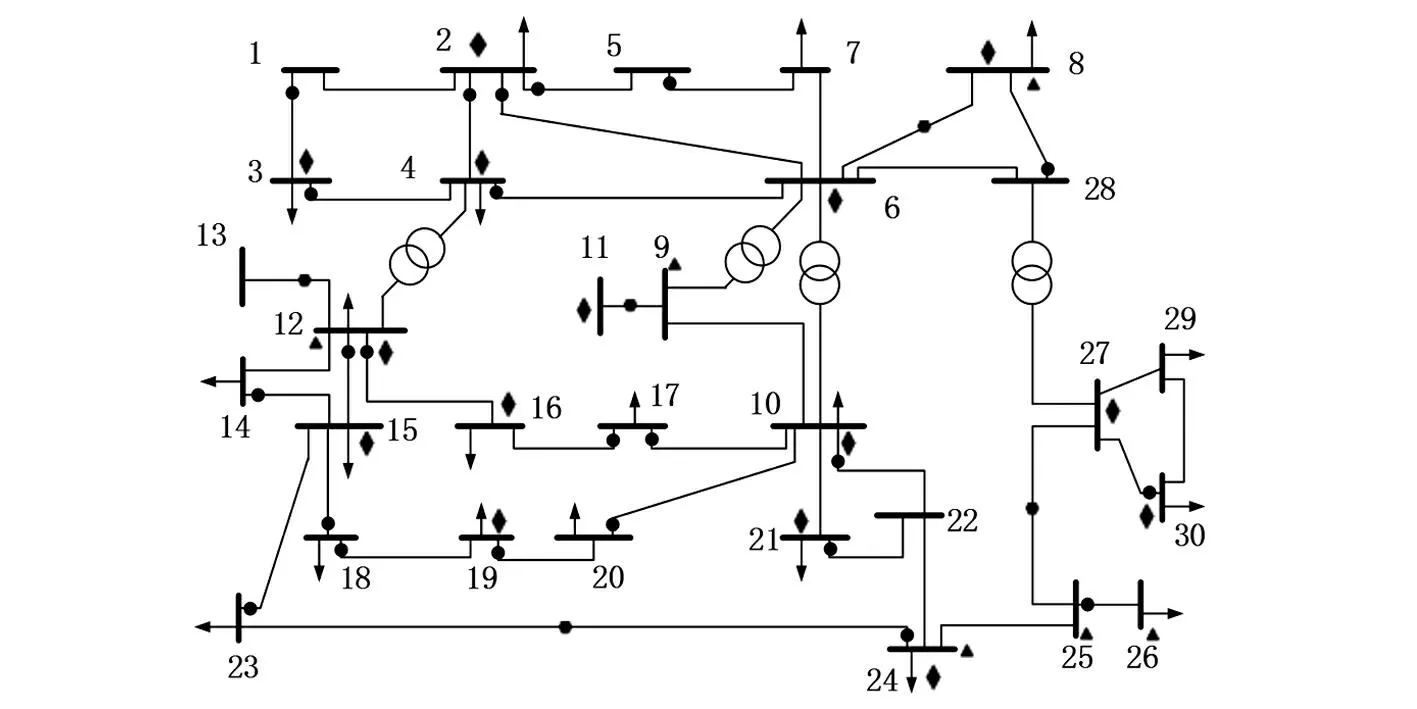
注：SCADA量測中 ●為支路潮流有功/無功功率； ◆為節點注入有功/無功功率； ■為節點電壓幅值;PMU量測中 為支路電流相量； ▲為節點電壓相量。圖1　IEEE 30節點網絡系統接線圖

本次實驗主要對以下幾種情況進行了如下分析。

1)狀態估計結果對比

圖2和圖3分別給出了所提方法、加權最小二乘算法、潮流真值的電壓幅值和相角的對比結果。

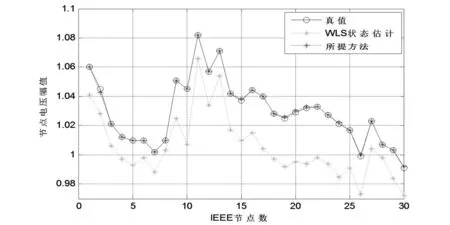
圖2　IEEE 30節點系統的電壓幅值對比結果

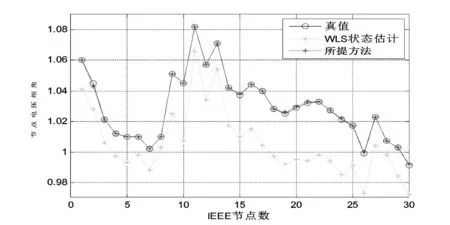
圖3　IEEE 30節點系統的電壓相角對比結果

為了更加清晰地對比所提方法，圖4、圖5給出了所提方法和加權最小二乘算法與真值的絕對誤差對比結果。

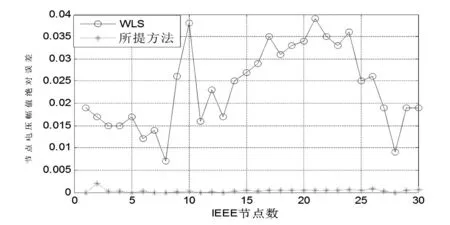
圖4　IEEE 30節點電壓幅值絕對誤差對比結果

圖5　IEEE 30節點電壓相角絕對誤差對比結果

通過圖4、圖5絕對誤差對比結果可以得出，所提出的方法對狀態估計結果有明顯的提高。

2)非關鍵量測量的檢測

在SCADA量測量中，對非關鍵量測量節點有功功率P4設置30%的量測誤差值。通過表格將較大的幾個量測殘差值列出來，如表1所示。

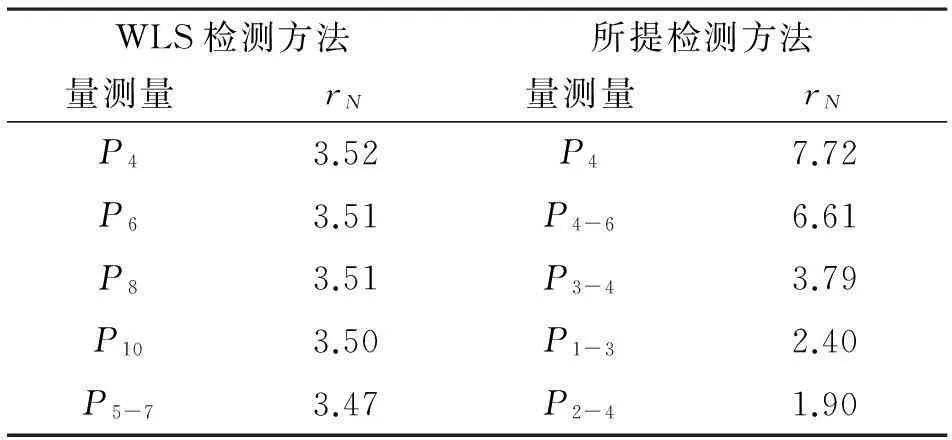
表1　IEEE 30節點系統非關鍵量測量標準化殘差值

為了進一步對比其他量測殘差值的大小，圖6、圖7將所有的SCADA量測量的標準化殘差值用直方圖展示出來。

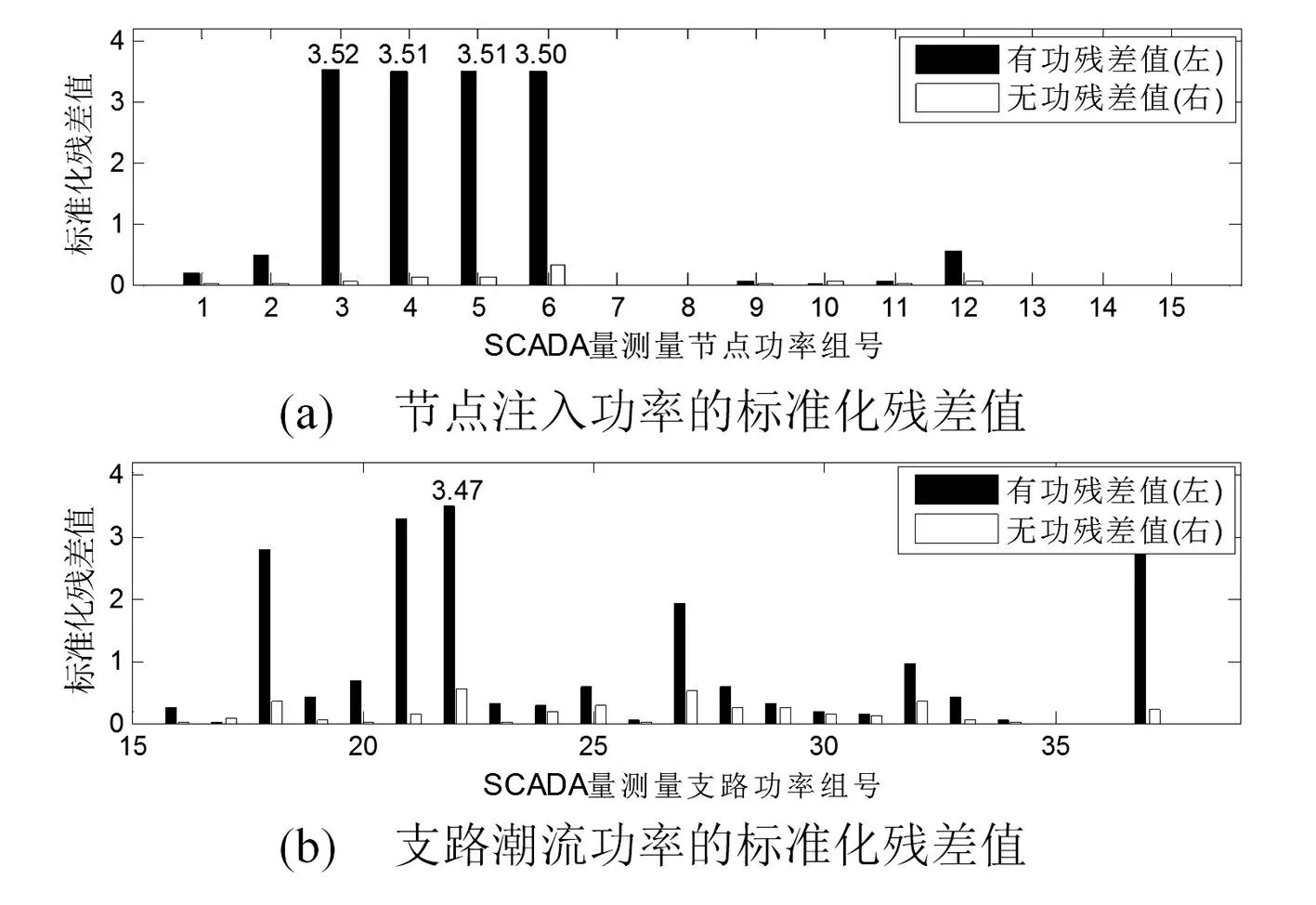
圖6　WLS狀態估計后的SCADA非關鍵量測量標準化殘差值

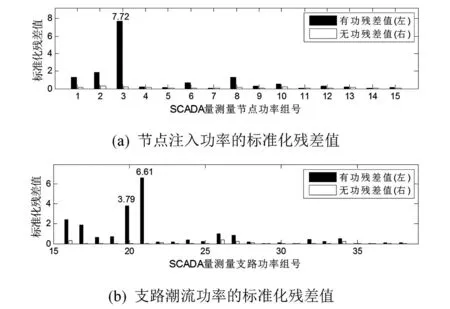
圖7　混合量測狀態估計后的SCADA非關鍵量測量標準化殘差值

對于非關鍵量測量中的不良數據，采用所提方法和WLS狀態估計算法都能將其檢測出來。

3)關鍵量測量的檢測

在SCADA量測量中，對關鍵量測量支路潮流無功功率Q24設置30%的量測誤差值，并將較大的幾個殘差值對應的量測量用列出來，如表2所示。

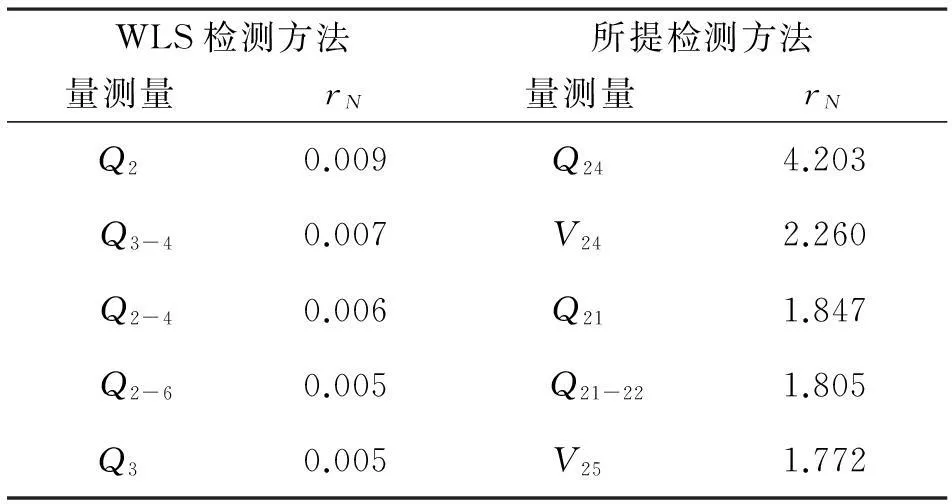
表2　IEEE 30節點系統關鍵量測量標準化殘差值

通過表2可以看出，通過加權最小二乘狀態估計算法計算各個量測量的標準化殘差值，所有量的測量殘差值都在檢測閾值范圍之內，無法將不良數據檢測出來，而通過混合量測狀態估計對殘差協方差矩陣更新后，可以看出量測量Q24的標準化殘差值大于閾值2.81，能夠被檢測出來。

為了對比其他殘差值的大小，圖8、圖9將所有的SCADA量測量的標準化殘差值用直方圖展示出來。

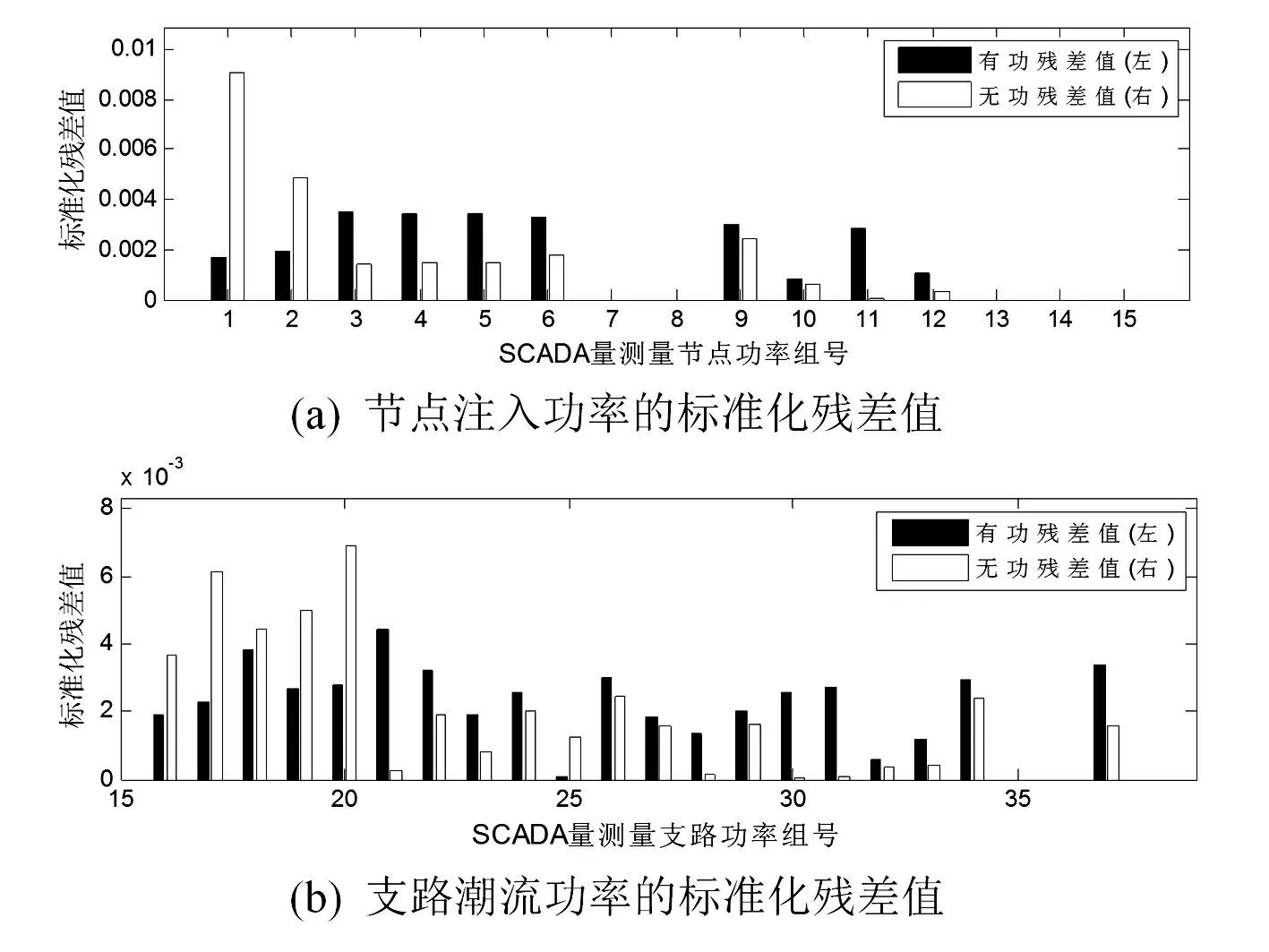
圖8　WLS狀態估計后的SCADA關鍵量測量標準化殘差值

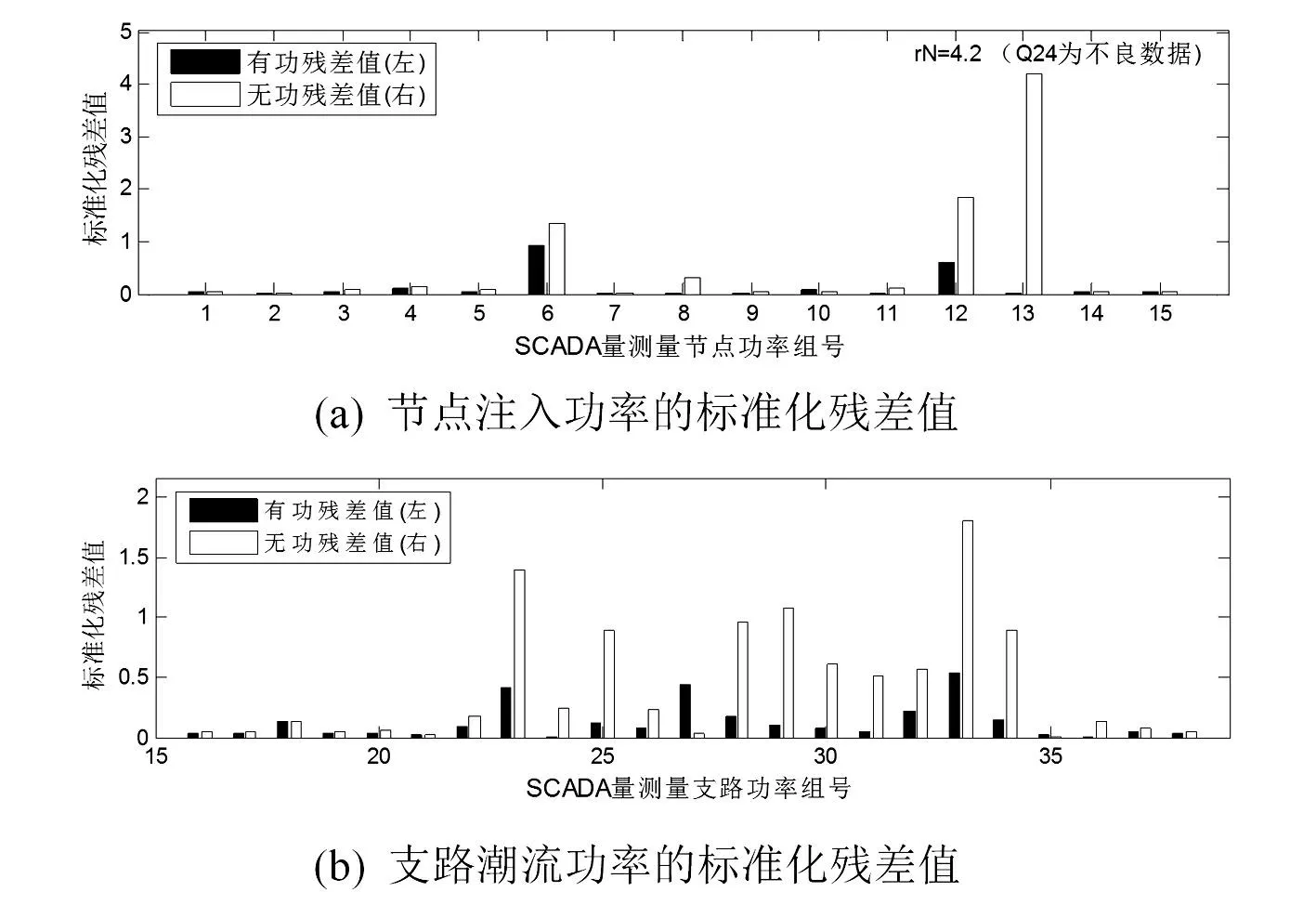
圖9　混合量測狀態估計后的SCADA關鍵量測量標準化殘差值

通過PMU量測量對殘差協方差矩陣更新后，當SCADA量測量中的關鍵量測量出現不良數據時，PMU量測量的標準化殘差值也將改變，如圖10所示。

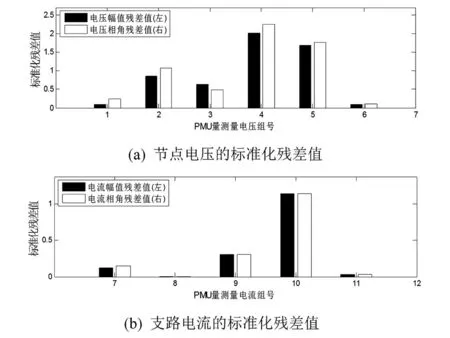
圖10　混合量測狀態估計后的PMU量測量標準化殘差值

根據實驗結果分析可知，所提狀態估計方法與僅有SCADA量測量的狀態估計的區別主要包括：1)量測量的冗余度不同：傳統狀態估計的量測量只是通過SCADA量測系統獲得，冗余度較低，系統中存在關鍵量測量；而混合量測狀態估計的量測量包含SCADA量測量和PMU量測量，冗余度高，不存在關鍵量測量。2)估計方式不同：傳統狀態估計只通過非線性狀態估計獲得估計結果，估計結果精度不高；而混合量測狀態估計方法將利用非線性狀態估計結果和PMU量測信息進行二次線性狀態估計，狀態估計結果的精度大大提高。

混合量測狀態估計方法的優點主要包括：狀態估計結果精度高，能夠檢測關鍵量測量中出現的不良數據。不足之處在于需要進行兩次狀態估計，需要多耗費一些時間。

4結語

充分利用PMU量測及SCADA量測值，討論并發展了一種基于PMU/SCADA混合量測的電力系統狀態估計及不良數據檢測方法。特別是當SCADA量測系統的關鍵量測量出現不良數據時，通過PMU量測量增加系統冗余度，同時利用二次線性狀態估計更新殘差協方差矩陣的方式來對SCADA量測量中的關鍵量測量中的不良數據進行檢測，通過IEEE 30節點系統對該方法進行了試驗，效果較好。

參考文獻

[1]李從善, 劉天琪, 李興源, 等. 用于電力系統狀態估計的WAMS/SCADA混合量測數據融合方法[J]. 高電壓技術, 2013, 39(11)：2686-2691.

[2]劉曉義, 宋佳音, 蔣輝雄, 等. 基于PMU/SCADA混合量測的電力系統狀態估計[J]. 電測與儀表,2012,49(559)： 11-15.

[3]薛輝, 賈清泉, 王寧, 等. 基于PMU量測數據和SCADA數據融合的電力系統狀態方法[J]. 電網技術, 2008,32(14)：44-49.

[4]李強, 周京陽, 于爾鏗, 等. 基于混合量測的電力系統狀態估計混合算法[J]. 電力系統自動化, 2005,29(19)：31-35.

[5]G. N. Korres, N. M. Manousakis. State Estimation and Bad Data Processing for Systems Including PMU and SCADA Measurements[J]. Electric Power Systems Research，2011(81)：1514-1524.

[6]P S Castro Vide, F P Maciel Barbosa, I M Ferreira. Combined Use of SCADA and PMU Measurements for Power System State Estimator Performance Enhancement[C]. Energetics (IYCE), Proceedings of the 2011 3rd International Youth Conference on. IEEE, 2011: 1-6.

[7]R. F. Nuqui, A. G. Phadke. Hybrid Linear State Estimation Utilizing Synchronized Phasor Measurements[J]. Power Tech, 2007 IEEE Lausanne，1665-1669.

中圖分類號：TM7

文獻標志碼：A

文章編號：1003-6954(2015)04-0051-05

作者簡介：

許勇(1988)，碩士研究生，主要研究方向為電力系統狀態估計。

(收稿日期：2015-03-09)

Abstract：A new state estimation method for bad data detection and identification based on PMU/SCADA hybrid measurement is presented by making full use of PMU and SCADA measurements. At first, the rapid decomposition state estimation is done on the condition of taking nodes' status values measured by SCADA, and then the linear state estimation is done with both state estimation results and PMU measurements. Meanwhile, whether there is bad data or not in critical measurements in SCADA is detected and identified by using the second linear state estimation to update the residual covariance matrix. Finally the effectiveness of the model is verified by the numerical calculation results of IEEE-30 bus system.

Key words：power system; phasor measurement unit (PMU); hybrid state estimation; bad data detection