一種基于改進粒子群算法的K-means算法

一種基于改進粒子群算法的K-means算法

林曉雪, 趙茂先

(山東科技大學 數學與系統科學學院，山東 青島 266590)

摘要：針對K-means算法對初始聚類中心敏感、算法容易收斂于局部解等問題，運用了增加飛行時間因子的粒子群算法，提高粒子群算法性能.利用改進的粒子群算法與K-means算法相結合，提高了基于粒子群算法的K-means算法性能．數值試驗驗證了提出算法的收斂性，且最優解的精度優于K-means算法、PSO算法和PSO-K算法．

關鍵詞：K-means算法；粒子群算法；飛行時間因子； PSO-K算法

中圖分類號：TP301.6 文獻標志碼：A

A K-means algorithm based on the improved

particle swarm optimization algorithm

LIN Xiao-xue, ZHAO Mao-xian

(College of Mathematics and Systems Science, Shandong University of Science and Technology, Qingdao 266590, China)

Abstract：Considering K-means algorithm was sensitive to the initial cluster centers and easy to converge to local solution and other issues, we increased flight time factor to improve particle swarm algorithm performance. The improved particle swarm algorithm and K-means algorithm were combined to improve the performance of K-means algorithm based on particle swarm optimization. Numerical experiments verified the proposed convergence of the algorithm, and the optimal solution accuracy was better than K-means algorithm, PSO algorithm and PSO-K algorithm.

Key words： K-means algorithm；PSO algorithm；flight time factor；PSO-K algorithm

K-means算法[1]是基于劃分的經典聚類算法，具有容易理解、實現簡單、收斂速度快等優點，但由于局部極值點的存在以及啟發算法的貪心性，使得傳統K-means算法有對初始聚類中心敏感、極易收斂于局部極值的缺點．目前，針對初始聚類中心的選取，許多研究者提出了不同改進算法．Jim等[2]提出了一種快速找到聚類中心的算法，該算法使用聚類中心的位移拒絕不可能的候選點，算法縮短了計算時間．Aliasa等[3]提出了修改后的移動K均值算法用來解決分割問題，修改后的算法是找到最近的中心為每個像素的更好聚類中心．Merwe等[4]率先提出用粒子群(Particle Swarm Optimization，PSO)算法解決聚類問題，文章介紹了粒子群算法是如何連接各個聚類中心，如何更好的實現K-means算法．Chen等[5]通過粒子群算法尋找聚類中心，根據聚類中心對粒子進行位置編碼．Niknam等[6]提出了基于粒子群算法、蟻群算法和K均值聚類分析的高效混合的方法．

在分析上述研究成果和K-means算法存在缺陷的基礎上，本文提出一種基于自適應飛行時間因子PSO算法的K-means算法．通過采用自適應飛行時間因子的PSO算法，動態調整粒子的飛行時間，避免了PSO算法中粒子出現早熟收斂的現象，消除K-means算法對初始聚類中心選取的依賴性，得到全局最優的N個聚類中心，然后以此為初始聚類中心執行改進的算法獲得理想的聚類劃分．

1基本算法簡介

1.1　K-means算法

K-means算法的基本原理是基于劃分的聚類算法，給定一組數據集X，數據總數n，首先隨機地選取k個初始聚類中心(聚點)，把每個對象分配給離它最近的聚點，從而得到一組聚類．然后，計算每個聚類的均值作為新的聚點，并把每個數據重新分配到最近的聚點，循環執行這一過程，直到滿足終止條件結束算法．

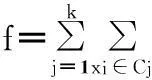
1.2　PSO算法

粒子群優化算法是一種基于群體智能方法的進化計算技術，最早由Kennedy和Eberhart[7]于1995年提出．粒子群算法就是粒子在d維空間搜索一個目標函數的最優解，在該空間中有N個粒子，粒子具有位置Zr和速度Vr，每個粒子的位置Zr代表了一個潛在解．將Zr代入目標函數就可以算出其適應度，根據適應度的大小來衡量解的優劣．第r個粒子目前自身搜索到的最好位置(pbest)為Pr，所有粒子目前搜索到的最優位置(gbest)記為Pg．最早期的PSO算法通過下面的公式來更新自己的速度和位置：

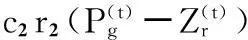
(1)

(2)

其中t是迭代次數；r1和r2為[0,1]之間均勻分布的隨機數，以增加搜索隨機性和種群的多樣性；c1和c2是學習因子，也稱加速因子，代表將每個粒子推向pbest和gbest位置的統計加速項權值．

為了提高基本PSO算法的性能，Shi等[8]提出了帶有慣性權重因子w的粒子群算法，后來稱這個改進的算法為標準粒子群算法(Stand Particle Swarm Optimization，SPSO)．SPSO算法將基本PSO算法中的速度更新公式改為下式：

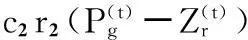
(3)

位置更新公式與基本PSO算法相同．上式中w稱為慣性權重因子，是一個非負數，用來控制粒子的全局搜索能力與局部搜索能力之間的平衡．w較大時，粒子搜索全局空間的趨勢較大，有能力探索新的區域，使算法全局搜索能力加強；反之w較小時，粒子局部搜索能力較強．w適中時PSO算法找到全局最優解的機會較大，鑒于以上分析，Shi等讓w隨迭代次數而線性遞減：

(4)

其中wmax為慣性權重初始值；wmin為慣性權重終值；tmax為最大迭代次數；t為當前迭代次數．實驗表明，這種改進明顯改善了算法的性能，因此后來的改進都在SPSO的基礎上進行的改進．

2PSO-K算法

由于K-means算法容易受初始聚類中心選取的影響，算法易收斂于局部極值．針對K-means算法的缺陷，不少學者提出了將優化算法與K-means算法相結合的算法，基于粒子群算法的k-means算法(PSO-K算法)是一種用粒子群算法的思想來解決聚類問題的優化算法，算法在一定程度上克服了K-means算法的缺陷．

2.1　PSO-K算法原理

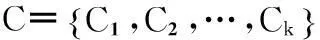
對于每個聚類中心的計算公式和樣本集總的類間離散度和公式如下：

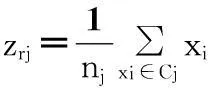
(5)

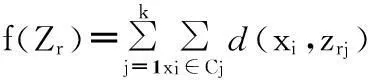
(6)

粒子的適應度按照公式(6)計算．其中Zr為第r個粒子(1≤r≤N)，N為粒子個數，zrj為第r個粒子的第j個類的聚類中心位置，d(xi,zij)為第i個樣本數據到對應聚類中心的距離．聚類準則函數f(Zr)為各類樣本到對應聚類中心的距離總和，也就是粒子的適應度函數．這里d(xi,zrj)為歐式空間距離．距離公式、粒子的速度和位置更新公式如下：

d(xi,zrj)=‖xi-zrj‖

(7)

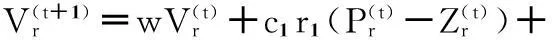
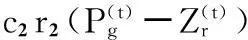
(8)

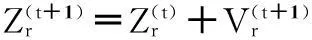
(9)

當聚類中心確定時，聚類的劃分由最鄰近法則確定，即每個數據優先劃分到離它最近的聚類．

2.2　PSO-K算法步驟

(1)種群初始化．給定樣本總數n，維數d，聚類個數k，先將每個樣本隨機指派為一類，作為最初的聚類劃分，根據公式(5)計算各類的聚類中心，作為粒子的初始位置編碼，初始化粒子速度，計算粒子的適應度．反復進行N次，共生成N個初始粒子；

(2)根據公式(6)、(7)計算每個粒子的適應度值；

(3)對每個粒子的適應度值和它所經歷的最好位置Pr的適應度值比較，如果更好，更新Pr；

(4)對每個粒子的適應度值和群體所經歷的最好位置Pg的適應度值比較，如果更好，更新Pg；

(5)根據公式(4)、(8)和(9)更新粒子的速度和位置；

(6)根據K-means算法中的最鄰近法則，將每個樣本重新歸類，得到新的聚類劃分；

(7)判斷是否滿足終止條件，如果滿足輸出最優解；否則返回(2)．

終止條件為粒子群的最好適應度值在給定的迭代數內幾乎不改變或達到給定最大迭代次數．

3改進的PSO-K算法

3.1　自適應飛行時間因子的PSO算法

最基本的PSO算法中粒子的位置更新公式為(2)，現在增加飛行時間因子T，T表示第r個粒子的飛行時間，在基本PSO算法中T=1，因此PSO算法中的位置更新公式變為以下公式：

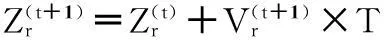
(10)

本文采用如下改進的飛行時間因子的計算方法：

T=F(αt,βt)=T0+αtTα-βtTβ

(11)

其中αt,βt分別表示種群多樣性和種群進化度；T0為T的初始值，一般取0.8~1.0；Tα,Tβ用來調節αt,βt對飛行時間因子的影響程度．αt用來表示粒子的聚集程度，粒子越聚集，種群的多樣性就越差；粒子越分散，種群多樣性越好，算法就越不容易陷入局部最優解．αt的公式表示如下：

(12)

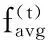
種群進化度指標βt．βt用來表示種群的進化程度，βt的公式表示如下：

(13)

由公式(13)可知βt的取值范圍，βt∈(0,1]．當βt=1時，表明算法沒有進化，如果在給定的次數下算法都沒有進化，可以認為算法找到了全局最優解或陷入了局部最優；當βt越小表示種群進化速度越快．

在進化初期βt值較小，此時粒子的飛行時間應該長點，即飛行時間因子T應較大．隨著進化程度的減慢，βt值逐漸增大，粒子的飛行時間應該逐漸減小．若較為分散，粒子群的多樣性就好，粒子群就不容易陷入局部最優．因此T的大小應該隨著粒子群的聚集程度增大而增大，隨著種群進化程度的降低而減小．即T隨著αt的增大而增大，隨著βt的增大而減小，從而可以將T表示為αt和βt的函數，即公式(11)所示．由于0<αt≤1,0<βt≤1，所以T0-Tβ

基于上述分析，基本的PSO算法就改為一種自適應改變飛行時間因子的PSO算法，相當于提高了PSO算法性能，增強了算法的收斂度．

3.2　改進的PSO-K算法步驟

本文提出的改進PSO-K算法是采用增加飛行時間因子的PSO算法，與K-means算法相結合從而提高PSO-K算法的收斂性．

改進的PSO-K算法具體步驟如下：

Step1 對粒子群進行初始化操作．給定固定參數w，c1，c2，vmin，vmax，T0，Tα，Tβ．從數據集X中隨機選擇k個中心點，將其作為粒子位置Zr的初值．同時初始化粒子的速度Vr、個體最優位置Pr和群體最優位置Pg．這一過程循環N次，可生成N個初始化粒子．

Step2 根據公式(6)、(7)，計算粒子的適應度值．

Step3 比較每個粒子的適應度值和它所經歷的最好位置Pr的適應度值，如果更好，更新Pr．

Step4 比較每個粒子的適應度值和群體所經歷的最好位置Pg的適應度值，如果更好，更新Pg．

Step5 根據速度公式(4)、(8)式和位置公式(10)-(13)分別更新粒子的速度和位置．

Step6 根據K-means算法中的最鄰近法則，將每個樣本重新歸類，得到新的聚類劃分．

Step7 判斷是否滿足終止條件，如果滿足輸出最優解；否則返回(2)．

終止條件為粒子群的最好適應度值在給定的迭代數內幾乎不改變或達到給定最大迭代次數．

4實驗結果及分析

本實驗為了驗證文中改進的PSO-K算法的有效性，采用的數據集為UCI數據集中經常用來測試聚類效果的數據集Iris數據集、wine數據集以及Breast Cancer數據集．

表1　測試數據集表

本文實驗參數設置如下：粒子群的種群規模N=20，加速因子c1=c2=2，粒子群的最大迭代次數tmax=100，threp=4，threg=5，粒子群的適應度方差閾值threσ=0.1．文中增加飛行時間因子的PSO算法中，在經過多次試驗之后，發現T0為0.8~1.0時算法效果較好，所以本文中T0=0.9．Tα和Tβ可以動態調整，一般較大的Tα會使算法容易跳過最優解陷入振蕩狀態，較大的Tβ會使算法容易陷入局部最優．經過多次實驗，發現Tα在0.05~0.1之間取值，Tβ在0.4~0.6之間取值時算法性能較好，本次試驗Tα和Tβ分別取值0.08和0.45．實驗中將K-means算法、PSO-K算法與文中算法進行比較，每種算法分別執行20次，測試結果取其平均值．算法的聚類準確率以及適應度值的比較分別見表2、表3．

由表2可知，無論是對低維Iris數據集，還是高維wine數據集和Breast Cancer數據集， K-means算法的聚類準確率最低，PSO-K算法比K-means算

表2　K-means、PSO-K算法與文中算法聚類準確率比較

表3　K-means、PSO-K算法與文中算法適應度值比較

法聚類效果好一些，相比之下文中算法聚類效果最好．由表3可知，無論是對低維Iris數據集，還是高維wine數據集和Breast Cancer數據集， K-means算法的適應度值最大，PSO-K算法比K-means算法的適應度值小一些，相比之下文中算法的適應度值最小．適應度值越小則表明聚類劃分得到的類內數據對象之間緊密程度越好，由此可知文中改進算法的聚類效果最好．

為了驗證算法的收斂性能，對Iris數據集進行測試得到三種算法的收斂曲線圖(圖1)．

圖1　三種算法的收斂曲線圖

從圖1中可以看出 K-means算法前期收斂速度最快，但算法容易收斂于局部解，PSO-K算法由于粒子群早熟收斂問題，收斂速度沒有K-means算法收斂速度快．文中改進算法由于增加了自適應飛行時間因子，提高了PSO算法性能，同時又對早熟收斂的粒子執行變異操作，這樣就增加了算法的收斂速度．所以文中算法的收斂性較理想．

5結束語

本文研究的基于粒子群算法的K-means算法是聚類分析研究的新的主流方向，通過采用自適應飛行時間因子的PSO算法與K-means算法相結合，提出了的改進的PSO-K算法．通過數值實驗，文中算法比K-means算法、PSO-K算法具有更優的全局收斂性，進而驗證了本文算法的可行性和有效性．然而與傳統K-means算法相比，文中算法的運算時間有所增加，如何提高K-means算法精確度并同時保持較快的計算速度，是進一步需要研究的課題．

參考文獻：

[1] Hartigan J A. Clustering Algorithms[M]. New York: John Wiley & Sons Inc, 1975.

[2] Jim Z C, Huang T J, Liaw Y C. A fast k-means clustering algorithm using cluster center displacement[J]. Pattern Recognition, 2009(42):2551-2556.

[3] Aliasa M F, Isa A M, Suaiman S A,etal. Modified moving k-means clustering algorithm[J]. International Journal of Knowledge-based and Intelligent Engineering Systems, 2012(16): 79-86.

[4] Merwe D W, Engelbrecht A P. Data Clustering using Particle Swarm Optimization[C]// Evolutionary Computation, 2003: 215-220.

[5] Chen C Y, Fun Y. Particle Swarm Optimization Algorithm and Its Application to Clustering Analysis[J].International Conference on Networks, 2004, 3(21): 789-794.

[6] Niknam T, Amiri B. An efficient hybrid approach based on PSO, ACO and k-means for cluster analysis[J]. Applied Soft Computing, 2010(10): 183-197.

[7] Kennedy J, Eberhart R. Particle Swarm Optimization[J]. International conference on neural network, 1995, 4(2): 1942-1948.

[8] Shi Y, Eberhart R. A Modified Particle Swarm Optimizer[C]// International conference on Evolutionary Computation Anchorage, 1998: 69-73.

(編輯：姚佳良)