基于模糊物元法的路面結(jié)構(gòu)性能評(píng)價(jià)指標(biāo)權(quán)重研究
基于模糊物元法的路面結(jié)構(gòu)性能評(píng)價(jià)指標(biāo)權(quán)重研究
喬中美
(河北省高速公路廊坊北三縣管理處廊坊065000)
摘要引用信息熵所反映出來(lái)的數(shù)據(jù)本身效用值來(lái)計(jì)算指標(biāo)的權(quán)重系數(shù),建立了基于熵權(quán)理論的模糊物元模型,有效地避免了權(quán)重分配困難的問(wèn)題。該模型根據(jù)路面結(jié)構(gòu)評(píng)價(jià)指標(biāo)具體分布情況,動(dòng)態(tài)計(jì)算路面結(jié)構(gòu)評(píng)價(jià)指標(biāo)的權(quán)重,克服了規(guī)范中所有路面評(píng)價(jià)指標(biāo)權(quán)重系數(shù)完全相同的不足,結(jié)果更具說(shuō)服力。結(jié)合實(shí)例,通過(guò)與規(guī)范標(biāo)準(zhǔn)計(jì)算結(jié)果比較,進(jìn)一步驗(yàn)證了該模型的合理性與實(shí)用性。
關(guān)鍵詞熵模糊物元權(quán)重路面結(jié)構(gòu)評(píng)價(jià)
DOI10.3963/j.issn.1671-7570.2015.02.029
收稿日期:2014-12-04
現(xiàn)行《公路技術(shù)狀況評(píng)定標(biāo)準(zhǔn)》(JTG H20-2007)給出的路面使用性能綜合評(píng)定指標(biāo)的權(quán)重為固定值,認(rèn)為各個(gè)公路中各項(xiàng)計(jì)算指標(biāo)所占權(quán)重相同,不能對(duì)不同的干線公路的使用性能差別對(duì)待。雖然計(jì)算過(guò)程簡(jiǎn)單,省去了很多麻煩,但是這也在一定程度上犧牲了計(jì)算結(jié)果精度及合理性。為了準(zhǔn)確評(píng)價(jià)各干線公路的使用性能,建立一套科學(xué)合理的路面綜合評(píng)價(jià)體系,許多專家學(xué)者都致力于這方面的研究。劉艷,康海貴等[1]將遺傳算法應(yīng)用到路面綜合評(píng)價(jià)模型之中;宋俊敏等[2]則探討了神經(jīng)網(wǎng)絡(luò)在路面綜合評(píng)價(jià)中的應(yīng)用;任重昕,劉雙[3]應(yīng)用灰色聚類法對(duì)林區(qū)路面性能進(jìn)行了綜合評(píng)價(jià)。以上研究雖然也解決了路面綜合評(píng)過(guò)程中不同公路差異性的問(wèn)題,但是當(dāng)路面檢測(cè)數(shù)據(jù)過(guò)于龐大時(shí),就會(huì)出現(xiàn)計(jì)算過(guò)程繁瑣,而且對(duì)計(jì)算人員的數(shù)學(xué)功底有很大要求。而且缺乏比較客觀可靠的確定評(píng)價(jià)因子權(quán)重的方法[4,5]。模糊物元理論常常用于研究不相容的問(wèn)題[6],適用于評(píng)價(jià)多指標(biāo)問(wèn)題,通過(guò)建立物元模型把求解問(wèn)題的過(guò)程形式化。本文將熵權(quán)理論引入到路況指標(biāo)權(quán)重的計(jì)算中,并結(jié)合模糊物元理論,能夠較客觀、全面地評(píng)價(jià)路面性能。
1模糊物元模型
1.1 基本概念
在模糊物元分析理論中事物M及其特征C和量值x組成物元R=(M,C,x)或R(M,C,C(M)),把事物的名稱M、量值x和特征C稱為物元3要素。如果物元模型中的量值x具有模糊性,便稱其為模糊物元。事物M有n個(gè)特征C1,C2,…,Cn及其對(duì)應(yīng)的量值x1,x2,…,xn,則稱R為n維模糊物元。m個(gè)事物的n維物元互相組合便構(gòu)成m個(gè)事物的n維復(fù)合模糊物元Rmn,即
(1)
式中:Rmn為m個(gè)事物的n個(gè)模糊物元;Mi為第i個(gè)事物(i=1,2,…,m);Ci為第j個(gè)特征(j=1,2,…,n);xij為第i個(gè)事物第j個(gè)特征對(duì)應(yīng)的模糊物元量值。
1.2 模糊物元從優(yōu)隸屬度
各單項(xiàng)指標(biāo)對(duì)應(yīng)的模糊量值從屬于標(biāo)準(zhǔn)方案對(duì)應(yīng)的評(píng)價(jià)指標(biāo)的模糊量值的隸屬程度,稱為從優(yōu)隸屬度。從優(yōu)隸屬度一般為正值,據(jù)此建立的準(zhǔn)則,稱作從優(yōu)隸屬度準(zhǔn)則。各評(píng)價(jià)指標(biāo)對(duì)于不同方案來(lái)說(shuō),有的是越小越優(yōu),而有的則是越大越優(yōu),因此,對(duì)于隸屬度不同時(shí)采用不同的計(jì)算公式,為了充分反映路面評(píng)價(jià)各項(xiàng)指標(biāo)的相對(duì)性,采用模型如下。
越大越優(yōu)模型:μij=Xij/maxXij
越小越優(yōu)模型:μij=Xij/minXij
式中:μij為從優(yōu)隸屬度;maxXij為各個(gè)方案中評(píng)價(jià)指標(biāo)中的最大值;minXij為各個(gè)方案中評(píng)價(jià)指標(biāo)中的最小值。
由此可以建立隸屬度從優(yōu)模糊物元矩陣:
(2)
1.3 模糊物元矩陣
標(biāo)準(zhǔn)模糊物元是指從優(yōu)隸屬度模糊物元Rmn中各評(píng)價(jià)指標(biāo)的從優(yōu)隸屬度的最大值或最小值。本文以路面結(jié)構(gòu)設(shè)計(jì)指標(biāo)的最大值作為最優(yōu),也就是各評(píng)價(jià)指標(biāo)從優(yōu)隸屬度均為1。若Δij(i=1,2,…,n;j=1,2,…,m)表示標(biāo)準(zhǔn)模糊物元Ron與復(fù)合從優(yōu)隸屬度模糊物元Rmn中各項(xiàng)差的平方,則組成差平方復(fù)合模糊物元Δ,即Δij=(μoj-μij)2,可表示為
(3)
2熵值法計(jì)算權(quán)重系數(shù)
在傳統(tǒng)路面結(jié)構(gòu)評(píng)價(jià)中,PCI,RQI,RDI,SRI等指標(biāo)的權(quán)重規(guī)范中規(guī)定的是定值,然而實(shí)際道路評(píng)價(jià)時(shí),對(duì)于不同的路面結(jié)構(gòu),各個(gè)指標(biāo)值分布大小和離散程度各不相同,加權(quán)計(jì)算時(shí),采用固定的權(quán)重明顯不合理。在信息理論中,熵值大小反映了信息無(wú)序化程度,其值越小,系統(tǒng)無(wú)序度越小,故可用信息熵評(píng)價(jià)所獲系統(tǒng)信息的有序度及其效用,即由路面評(píng)價(jià)指標(biāo)值組成的判斷矩陣確定各項(xiàng)指標(biāo)權(quán)重大小,這種方法可以盡量消除每種指標(biāo)權(quán)重確定時(shí)人為的干擾,計(jì)算結(jié)果更符合實(shí)際工程情況。其具體計(jì)算過(guò)程如下。
(1) 構(gòu)建m個(gè)事物n個(gè)評(píng)價(jià)指標(biāo)的判斷矩陣R=(xij)mn(i=1,2,…,n;j=1,2,…,m)。
(2) 歸一化計(jì)算判斷矩陣,得到判斷矩陣B
(4)
式中:xmax為路面評(píng)價(jià)指標(biāo)中最滿意者;xmin為路面評(píng)價(jià)指標(biāo)中最不滿意。
(3) 根據(jù)熵權(quán)理論的定義,m個(gè)待評(píng)價(jià)事物分別具有n個(gè)評(píng)價(jià)指標(biāo),各評(píng)價(jià)指標(biāo)的熵可以依據(jù)下式確定。
(5)
(6)
當(dāng)fij=0時(shí),為使lnfij有意義,可以將lnfij理解成一很大的數(shù),當(dāng)其fij相乘時(shí)結(jié)果趨近于0,故可認(rèn)為fijlnfij=0。但當(dāng)fij=1,fijlnfij也等于0,這顯然與實(shí)際情況不符,故需對(duì)fij進(jìn)行修正,其定義
(7)
(4) 評(píng)價(jià)指標(biāo)體系的熵權(quán)W計(jì)算
(8)
(9)
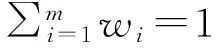
3路面結(jié)構(gòu)性能評(píng)價(jià)的應(yīng)用
《公路瀝青路面設(shè)計(jì)規(guī)范》(JTGD50-2006)中路面使用性能評(píng)價(jià)PQI=wPCI×PCI+ wRQI×RQI+wRDI×RDI+wSRI×SRI。對(duì)于各項(xiàng)權(quán)重為定值,本文應(yīng)用權(quán)重分析法確定各項(xiàng)權(quán)重。以廊坊某條公路檢測(cè)數(shù)據(jù)為例,路面結(jié)構(gòu)檢測(cè)結(jié)果見(jiàn)表1。
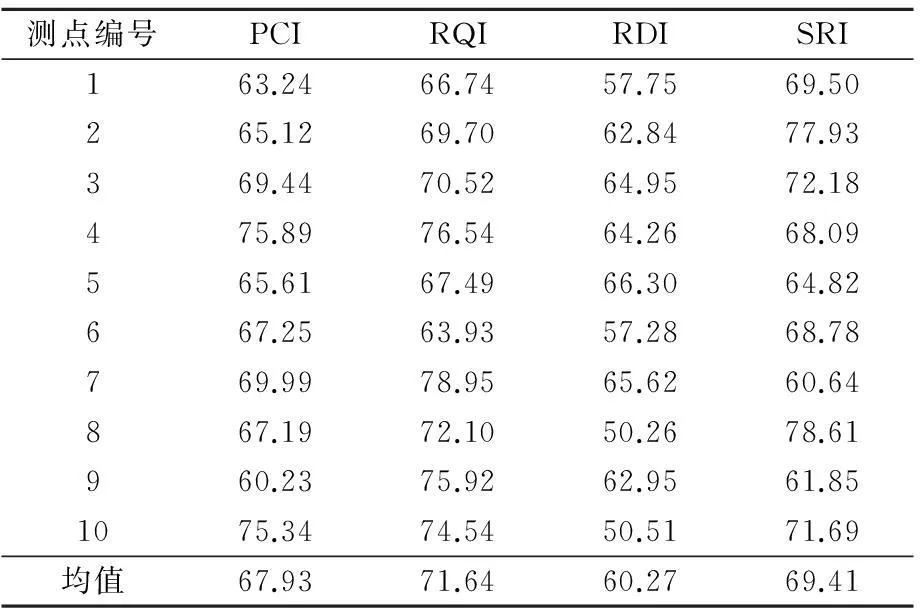
表1 路況指標(biāo)檢測(cè)結(jié)果
對(duì)于一條公路,將每一個(gè)檢測(cè)點(diǎn)看成是樣本點(diǎn)。權(quán)重計(jì)算步驟如下。
3.1 建立評(píng)價(jià)模型
(1) 構(gòu)建復(fù)合模糊物元。根據(jù)表1數(shù)據(jù),對(duì)10個(gè)測(cè)點(diǎn)的4個(gè)指標(biāo)進(jìn)行復(fù)合模糊物元。
(2) 根據(jù)式(2)、式(3),以越大越優(yōu)原則構(gòu)建從優(yōu)隸屬度模糊物元。
(3) 根據(jù)標(biāo)準(zhǔn)模糊物元Rmn和構(gòu)建差平方模糊復(fù)合物元RΔ。

(4) 用熵值法確定權(quán)重。根據(jù)式(5)構(gòu)造歸一化判斷矩陣B。

由式(6)和式(7)計(jì)算可得熵Hi=(1.105 31.099 71.067 11.062 6)T和wi=(0.314 30.297 60.201 10.168 9)T,i=(1,2,3,4)。計(jì)算結(jié)果與《公路技術(shù)狀況評(píng)定標(biāo)準(zhǔn)》相比較,見(jiàn)表2。

表2 路面評(píng)價(jià)指標(biāo)權(quán)重對(duì)比結(jié)果
依據(jù)表2中各項(xiàng)評(píng)價(jià)指標(biāo)權(quán)重計(jì)算表1中各項(xiàng)指標(biāo)加權(quán),得到PQI分布情況見(jiàn)圖1。
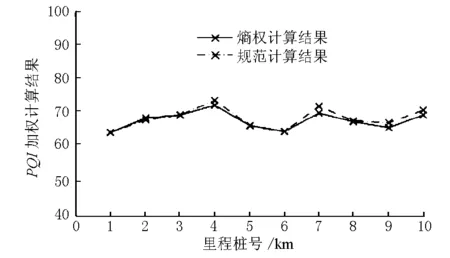
圖1 PQI分布結(jié)果對(duì)比
由表2、圖1可見(jiàn),基于熵權(quán)理論計(jì)算得到的路面結(jié)構(gòu)評(píng)價(jià)指標(biāo)權(quán)重與規(guī)范中的規(guī)定值雖然存在一定的偏差,但是整體趨勢(shì)相同;利用上述權(quán)重系數(shù)計(jì)算得到的PQI指標(biāo)略小于依據(jù)規(guī)范中固定權(quán)重計(jì)算的結(jié)果,該結(jié)果可以更加真實(shí)地反映路面結(jié)構(gòu)各個(gè)性能指標(biāo)的實(shí)際情況。
4結(jié)語(yǔ)
將熵值理論與模糊物元模型相結(jié)合,應(yīng)用路面結(jié)構(gòu)綜合評(píng)價(jià)中克服了原有路面結(jié)構(gòu)評(píng)價(jià)方法中各個(gè)控制指標(biāo)權(quán)重固定不變的缺點(diǎn),通過(guò)動(dòng)態(tài)確定指標(biāo)權(quán)重,充分考慮了不同路面結(jié)構(gòu)指標(biāo)分布趨勢(shì)變化,更具有針對(duì)性。通過(guò)實(shí)例分析結(jié)果可以看出,該種方法計(jì)算得到的各個(gè)指標(biāo)權(quán)重與規(guī)范中規(guī)定值整體趨勢(shì)相近,可以應(yīng)用于實(shí)際工程。
參考文獻(xiàn)
[1]劉艷,康海貴,孫敏.基于遺傳算法的模糊優(yōu)選神經(jīng)網(wǎng)絡(luò)路面性能評(píng)價(jià)模型[J].大連理工大學(xué)學(xué)報(bào),2010(1):117-122.
[2]宋俊敏,李明,范虎彪,等.基于BP神經(jīng)網(wǎng)絡(luò)的路面使用性能評(píng)價(jià)方法研究[J].公路,2008(12):140-144.
[3]任重昕,劉雙.灰色聚類法在林區(qū)路面性能綜合評(píng)價(jià)中的應(yīng)用[J].東北林業(yè)大學(xué)學(xué)報(bào),2012(2):114-117.
[4]李濟(jì),李巖,李德峰.基于改進(jìn)AHP法定權(quán)的模糊優(yōu)選模型在地下水質(zhì)評(píng)價(jià)中的應(yīng)用[J].華北水利水電學(xué)院學(xué)報(bào),2002,23(2):4-6.
[5]劉慧,龔士良.集對(duì)分析及在地下水環(huán)境質(zhì)量評(píng)價(jià)中的應(yīng)用[J].工程勘察,2000(5):16-18.
[6]蔡文.物元模型及應(yīng)用[M].北京:科學(xué)技術(shù)文獻(xiàn)出版社,1994.

