核天體物理反應率擬合方法研究

核天體物理反應率擬合方法研究

周勇1,2，李志宏1，張海黔2

(1.中國原子能科學研究院 核物理研究所，北京102413；

2.南京航空航天大學 材料科學與技術學院，江蘇 南京211100)

摘要：為進行大規模核天體網絡運算，通常將核天體物理反應率擬合為與溫度相關的數值表達式，以簡化程序中的核物理輸入量。通過分析國際上常用的幾種核天體物理數據庫，本工作得到了一種新的擬合方法，其對反應率的擬合精度較目前國際上通用的REACLIB和NACRE數據庫的擬合方法的有明顯改善。該擬合方法適用于直接反應和窄共振、寬共振、閾下共振和多諧共振反應，方便建立核天體物理反應率數據庫。

關鍵詞：核天體物理反應率；擬合方法；相對離差

中圖分類號：O571.4 文獻標志碼：A

收稿日期：2014-09-10;修回日期：2014-12-12

作者簡介：周勇(1992—)，男，四川廣安人，碩士研究生，粒子物理與原子核物理專業

doi：10.7538/yzk.2015.49.11.1921

Study on Fitting Method

for Nuclear Astrophysics Reaction Rate

ZHOU Yong1,2, LI Zhi-hong1, ZHANG Hai-qian2

(1.ChinaInstituteofAtomicEnergy,P.O.Box275-46,Beijing102413,China；

2.CollegeofMaterialScienceandTechnology,

NanjingUniversityofAeronauticsandAstronautics,Nanjing211100,China)

Abstract:In large-scale nuclear astrophysics network computing, the nuclear astrophysics reaction rates were usually fitted to numerical reaction rates concerning temperature in order to reduce the input nuclear parameters. By analyzing the existing databases adopted internationally, a new fitting method was present in this paper, which can give much better fitting results than REACLIB and NACRE. This new fitting method can be applicable to direct reaction rates, isolated and narrow resonance reaction rates, multi-resonant reaction rates, subthreshold states and broad low energy resonances reaction rates, and is convenient to build nuclear astrophysics reaction rate data library.

Key words：nuclear astrophysics reaction rate; fitting method; relative scatter

核天體物理反應率是恒星演化研究中的重要物理量，它決定了核反應的路徑，進而影響恒星演化的進程。核天體物理網絡計算涉及數以萬計的帶電粒子和中子的核反應、核衰變以及它們隨溫度的變化曲線。盡管理論上可輸入與這些核反應、核衰變相關的核物理參數，通過微積分運算求解任何溫度下的天體物理反應率，但實際網絡計算中由于參數多，程序需要耗費巨大的CPU運行時間，計算效率非常低。

為解決這個問題，實際運用中常把核天體物理反應率擬合成與溫度相關的數值表達式，以簡化核反應程序對質量、電荷、能量、幾何參數以及反應截面等核反應參數的調用，從而提高網絡計算的效率。經相應擬合后，核天體物理反應率的解析表達式轉化為與溫度相關的純粹的數值表達式，弱化了物理參量的影響，擬合函數不再有明確的物理意義。

目前國際上常用的核天體物理數據庫主要有REACLIB[1]和NACRE[2]，它們采用各自推導的擬合公式將反應率數值化，并制成核反應率數據庫，可為核反應的網絡計算程序所調用。本工作擬分析比較REACLIB和NACRE數據庫采用的擬合方法，以提出一種精度更高的擬合公式。

1核天體物理反應率

在恒星物質中，恒星氣體的原子核之間的相對運動速度的分布φ遵從Maxwell-Boltzmann分布：

(1)

其中:T為氣體溫度；m為原子核質量；v為原子核之間的相對運動速度；k為Boltzmann常數。

對于兩體反應，核天體物理反應率可表示為它們的相對速度與反應截面σ(v)的卷積：

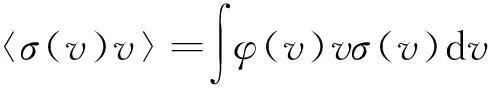
(2)

在實際計算中，采用質心系速度v和約化質量μ，將式(1)代入式(2)，并利用E=μv2/2，可得：

(3)

考慮天體物理S因子隨能量的變化較反應截面的變化更平緩，為方便外推，通常用天體物理S因子代替式(3)中的反應截面，S因子為：

(4)

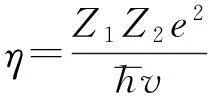
(5)

2反應率的擬合方法

反應率表達式(式(5))中的積分項通常無解析解，因此必須采用近似方法或數值積分的辦法求解反應率。

NACRE數據庫對于直接反應采用的擬合形式為：

(6)

NACRE數據庫對于共振反應采用的擬合形式為：

(7)

(8)

(9)

(10)

式中：下標NR+tail代表非共振和尾貢獻，r、MR、SR、BR分別代表窄共振、多諧共振、閾下共振、寬共振；Nrate為所取T的最高次數；E0(T)、Er分別為伽莫夫峰和共振峰對應能量；Γ為共振峰半高寬；C0、C1、D1～5、ci等為擬合系數。總的反應率為式(6)～(10)的和。

REACLIB數據庫對于直接反應和共振反應均采用下式擬合：

a4T1/3+a5T+a6T5/3+a7lnT)

(11)

當直接和共振過程同時存在時，總反應率可表示為兩個表達式(式(11))之和。

不同的擬合公式擬合同一組實驗數據時給出的擬合誤差不同，而同一種擬合公式擬合不同實驗數據時的擬合效果也有較大差別。另外，實驗給出的反應率數據存在相應精確度及可信度，這對擬合也存在一定影響。統一討論擬合公式的系統誤差存在較大難度。為簡化討論，在具體擬合時假定實驗數據絕對精準，且均可信。由于目前對反應率的實驗測量誤差遠小于擬合過程產生的誤差，所以上述假定是合理的。通常用相應的評價指標對比給出不同擬合公式的擬合精度，從而說明擬合公式的優越性。

為分析擬合結果的誤差，定義相對離差r作為評價指標：

(12)

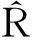
根據定義，r直接反映數據點的擬合情況，擬合數據與實驗數據差別越小，即r越接近0，表明擬合效果越好。rmax反映了一組數據中擬合值與實驗值偏差最大的情況，即能將該組數據擬合誤差約束在內的精度。

為方便比較，將NACRE擬合直接反應的公式中的多項式取到T5項，使得它與REACLIB同樣有7個擬合參數。用REACLIB方法擬合李二濤[3]所給直接輻射俘獲反應6He(p,γ)7Li的天體物理反應率，擬合結果給出的rmax=0.1%。NACRE方法擬合同樣數據得到的rmax=0.2%。可看出，對直接輻射俘獲反應而言，REACLIB公式的擬合精度較NACRE的好。對于包含窄共振的7Li(p,γ)8Be反應[2]，REACLIB公式擬合的rmax=0.8%，NACRE方法擬合的有效區域內rmax=11%。它們擬合結果的比較示于圖1。可看出，NACRE擬合方法的擬合相對離差分布較REACLIB大很多，擬合精度遠不及REACLIB。對于包含閾下共振能級的13C(α,n)16O反應[4]，REACLIB方法擬合的rmax=1.3%，較NACRE方法得到的rmax=9%好[2]。對于含有多個共振能級的復雜核反應9Be(α,n)12C[2]，REACLIB方法擬合該反應的rmax=15%，NACRE方法在使用較多的擬合參數時給出了rmax=10%的稍好結果。總之，通過本工作的比較分析發現，絕大多數情況下，REACLIB方法的擬合精度較NACRE的高。

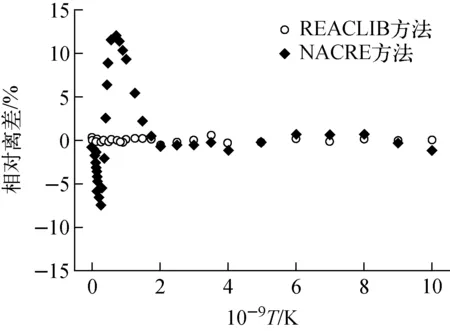
圖1　REACLIB與NACRE方法 擬合 7Li(p，γ) 8Be反應率的比較 Fig.1　Comparison of 7Li(p，γ) 8Be reaction rate fitted by REACLIB and NACRE methods

在關鍵的核天體物理網絡計算中，對核天體物理反應率的精度要求較高。比如，對于s過程路徑上的核反應，反應率的精度要求在5%以內[5]，而部分關鍵核(如純s過程、瓶頸和分支點涉及的核素)的反應率精度要求在1%以內[6]。對于大部分反應，REACLIB方法均能達到要求，但對于某些S因子隨能量變化劇烈且含有復雜多級共振的核反應，REACLIB方法也無法達到網絡計算要求的精度。使用擬合精度差的天體物理反應率進行計算，不僅會給模型計算帶來很大的不確定性，也會讓人們為提高實驗精度的所有付出付諸東流，因此有必要尋找更好的核天體物理反應率擬合公式。

3對擬合公式的改進

考慮到REACLIB對于直接反應的擬合精度較NACRE的好，結合REACLIB與NACRE后，給出一新的擬合公式：

(13)

式中：第1個e指數項為直接反應REACLIB公式的形式且增加了a7這一項，是對直接反應的擬合，該項只是在數值方法上提高了擬合精度，并無明確的物理意義；第2個e指數項為共振反應NACRE公式的形式，是對閾下共振和寬共振的擬合；第3個e指數項為共振反應NACRE公式對窄共振與多諧共振的擬合形式。

第1個e指數項中增加了a7項后，擬合反應2H(d,n)3He[7]的rmax=0.3%，而REACLIB公式擬合的rmax=0.7%。更多的擬合結果表明：添加a7項能改善擬合效果。

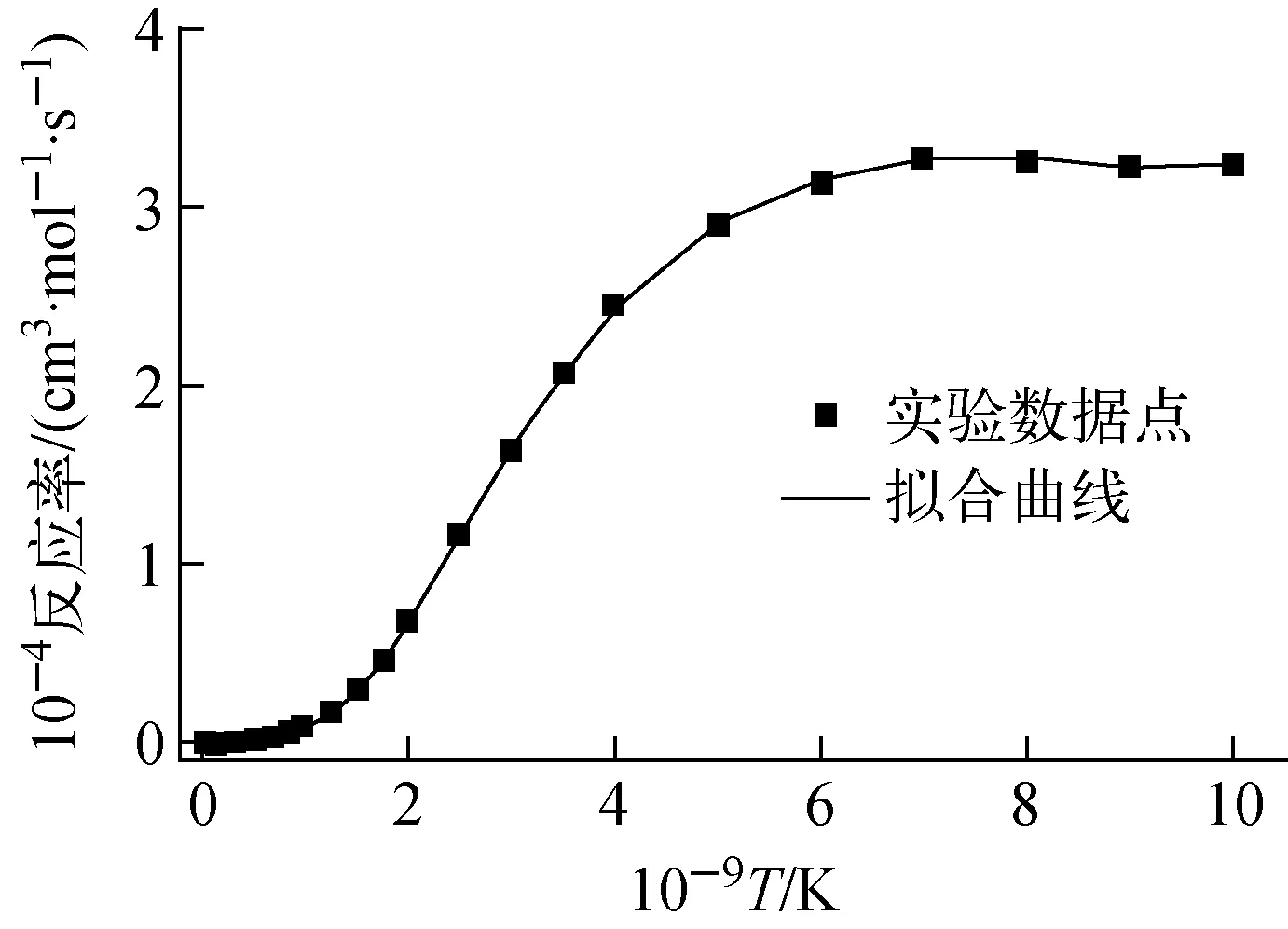
圖2　本工作得到的擬合方法 擬合 9Be(p，γ) 10B的反應率-溫度曲線 Fig.2　Curve of 9Be(p，γ) 10B reaction rate vs temperature fitted by new fitting method

在數值分析中，采用不同的函數族得到的擬合形式具有不同的擬合精度。經檢驗，發現添加T7/3形式的項較添加其他形式的項，如T8/3、T2、T3、ln(T+1)等更好。REACLIB公式擬合中T的指數系列為0、-1、-1/3、1/3、1、5/3、7/3，這種形式也要較其他指數系列，如0、-1、1、2、3、4、5和0、-1、-1/3、1/3、2/3、1、4/3的形式要好。

利用本工作得到的擬合方法擬合寬共振反應9Be(p,γ)10B[2]的反應率，得到的擬合系數如下：a1=-7.604 015，a2=0.003 624，a3=-12.447 558，a4=39.352 005，a5=-18.774 197，a6=-18.670 023，a7=4.659 769，a8=6.114 395，a9=21.124 178，a10=27.844 288，a11=4.994 859，a12=9.635 295，a13=14.123 683，a14=-1.228 151。與實驗給出的反應率數據相比，擬合的rmax=1.1%。從圖2所示的本工作得到的擬合方法擬合9Be(p，γ)10B的反應率-溫度曲線可看出，擬合數據點與原實驗數據點在低溫區和高溫區均符合非常好。

利用本工作得到的擬合方法擬合復雜共振反應9Be(α,n)12C[2]的rmax=4%，較REACLIB方法給出的結果rmax=15%以及NACRE方法給出的結果rmax=10%均好。對于寬共振反應9Be(p,γ)10B[2]，本擬合方法得到的rmax為1.1%，好于REACLIB方法與NACRE方法的結果rmax=1.2%與rmax=7%。對于寬共振反應10B(p,γ)11C[2]，本工作得到的rmax=0.6%，也好于REACLIB方法的rmax=1.8%與NACRE方法的rmax=13%。擬合效果可從圖3所示的本工作擬合的10B(p，γ)11C反應率與REACLIB數據庫的比較明顯看出。更多的擬合結果也表明，本工作得到的擬合方法較REACLIB方法和NACRE方法的擬合效果有明顯改善。

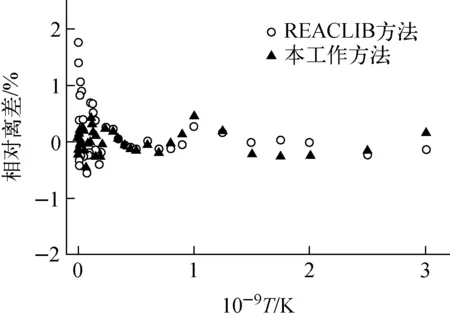
圖3　本工作擬合的 10B(p，γ) 11C反應率 與REACLIB數據庫的比較 Fig.3　Comparison of 10B(p，γ) 11C reaction rate fitted by new fitting method and REACLIB

無論目前國際上通用的核天體物理反應率擬合公式還是本工作得到的擬合方法，均只針對實驗數據涉及的溫度范圍內的反應率進行擬合。由于外推過程中的誤差無法準確估計，且通常外推計算存在較大的誤差(>10%)，擬合公式不適用于實驗涉及溫度范圍外的反應率的計算，即不能外推計算。

4結論

本工作系統研究了核天體物理反應率的擬合方法，使用REACLIB和NACRE數據庫給出的公式擬合了大量實驗數據，結果發現兩者的擬合精度仍不能滿足核天體物理網絡計算的要求。為改進REACLIB的擬合公式，通過增加對擬合反應率較敏感的T7/3項，并將多種共振反應相關的參數項添加到擬合公式中，形成包含14個待定系數的擬合方程。該擬合方法涵蓋了所有核反應的類型，適用于任何核反應數據的擬合。與已有的天體物理反應率數據庫相比，改進后的擬合方法有如下優點：

1) 適用范圍廣，可進行天體物理反應網絡中的任何反應類型的擬合；

2) 擬合精度高，即使是相當復雜的多共振9Be(α, n)12C反應體系，本擬合公式可給出相對離差小于4%的擬合精度，好于REACLIB數據庫給出的15%和NACRE數據庫給出的10%；

3) 統一性好，避免了REACLIB和NACRE直接反應用一種公式、有共振時用另一種公式的擬合方法，適用于建立標準化的核天體物理反應率數據庫。

參考文獻：

[1]RAUSCHER T, THIELEMANN F K. Tables of nuclear cross sections and reaction rates: An addendum to the paper “Astrophysical reaction rates from statistical model calculations”[J]. Atomic Data and Nuclear Data Tables, 2001, 79(1): 47-64.

[2]ANGULO C, ARNOULD M, RAYET M, et al. A compilation of charged-particle induced thermonuclear reaction rates[J]. Nuclear Physics A, 1999, 656(1): 3-183.

[3]李二濤.6He(p，γ)7Lig.s.和11B(p，γ)12Cg.s.天體物理S因子和反應率的間接測量[D]. 鄭州：鄭州大學，2009.

[4]郭冰. 利用(d，p)反應確定不穩定核的天體物理(p，γ)反應率[D]. 北京：中國原子能科學研究院，2007.

[5]KAPPELER F. Reaction cross sections for the s, r, and p process[J]. Prog Part Nucl Phys, 2011, 66: 390-399.

[7]CHRISTIAN L. Nuclear physics of stars[M]. Berlin: Wiley-VCH, 2007: 171-177.