級聯雙穩隨機共振和基于 Hermite 插值的局部均值分解方法在齒輪故障診斷中應用

第一作者李永波男，博士生，1986年8月生

通信作者徐敏強男，教授，博士生導師，1960年生

級聯雙穩隨機共振和基于Hermite插值的局部均值分解方法在齒輪故障診斷中應用

李永波,徐敏強，趙海洋，張思楊，黃文虎

(哈爾濱工業大學深空探測基礎研究中心，哈爾濱150001)

摘要：針對于弱信號在齒輪故障中難以提取問題，提出了一種基于級聯雙穩隨機共振 (Cascaded Bistable Stochastic Resonance，CBSR)降噪和局部均值分解(Local Mean Decomposition，LMD)齒輪故障的診斷方法。隨機共振可有效削弱信號中的噪聲，利用噪聲增強故障信號的微弱特征；LMD方法可自適應將復雜信號分解為若干個具有一定物理意義上PF分量之和，適合處理多分量調幅調頻信號。首先將振動信號進行CBSR消噪處理，然后對消噪信號進行LMD分解，通過PF分量的幅值譜找到齒輪的故障頻率。通過齒輪磨損故障診斷的工程應用，表明該方法可以有效提取齒輪故障微弱特征，實現齒輪箱的早期故障診斷。

關鍵詞：級聯雙穩隨機共振 局部均值分解 故障診斷 齒輪

基金項目：國家自然科學基金資助項目(10772061)

收稿日期：2013-09-09修改稿收到日期：2014-02-20

中圖分類號:TH165.3文獻標志碼：A

Application of cascaded bistable stochastic resonance and Hermite interpolation local mean decomposition method in gear fault diagnosis

LIYong-bo,XUMin-qiang,ZHAOHai-yang,ZHANGSi-yang,HUANGWen-hu(Deep Space Exploration Research Center, Harbin Institute of Technology, Harbin 150080, China)

Abstract:Aiming at the difficulty of extracting the weak signal in gear fault diagnosis, a method for gear fault diagnosis based on cascaded bistable stochastic resonance(CBSR)denoising and local mean decomposition(LMD)was proposed. The technique of stochastic resonance can remove noise in signals effectively and make use of noise to strengthen the weak fault feature; LMD can decompose a complicated signal into several stationary PF (product function) components with reality meanings, so it is very suitable to analyze the multi-component amplitude-modulated and frequency-modulated signals. Here, the CBSR was employed in the pretreatment to remove noise in vibration signals, the denoised signal was decomposed with LMD, and then the fault frequency of gear was found by inspecting the amplitude spectra of PF components. The engineering application of the method in fault diagnosis of gear wear demonstrated that it can extract the weak feature of gear fault effectively and realize the early gear fault diagnosis.

Key words:cascaded bistable stochastic resonance; local mean decomposition; fault diagnosis; gear

在實際的旋轉設備中，由于現場環境惡劣，例如振動傳遞路徑的多變、強背景噪聲以及多分量的振動源激勵等，導致測點信號的信噪比低、特征微弱且噪聲污染信號嚴重[1]。因此在設備早期故障階段，特征信號往往會被淹沒，難以實現早期故障診斷。微弱特征提取方法較多，多是以盡量消除或抑制噪聲為主，然而對于特殊非線性系統，此方法在降低噪聲同時也削弱了特征信號。隨機共振[2]是利用輸入信號的噪聲，在非線性系統的協同作用下達到共振輸出，使能量從高頻向低頻轉移，從而在削弱噪聲的同時加強微弱信號，實現微弱的特征有效提取。文獻[3]提出了采用級聯雙穩隨機共振的方法，使能量不斷從高頻向低頻轉移，即高頻噪聲能量逐級削減，低頻調制信號能量逐級被加強，適用于從強背景噪聲下提取微弱信號。

對齒輪進行故障診斷時，多采用振動信號來獲取齒輪故障的特征，由于齒輪在傳遞過程中產生振動信號為多分量的調幅調頻信號，在處理過程中常采用時頻的處理方法如：窗口傅里葉變換[4]、小波變換[5]和Hilbert-Huang[6]變換(HHT)等。但這些方法都有局限性，窗口傅里葉變換的時頻窗口不可調，小波變換的時頻窗口雖可調，但對信號的局部特征不具有自適應性。HHT是一種自適應的信號處理方法,但是在解調過程中會出現端點效應、模態混淆和無法解釋的負瞬時頻率等。在此基礎上Smith等[7-8]提出一種新的自適應的時頻分析方法-局部均值分解LMD,并首先在腦電圖領域上使用。LMD可將一復雜的疊加信號分解為一系列的PF(Product Function)分量和一個余項之和，每個PF分量是由一個包絡信號a(t)和一個純調頻信號sn(t)相乘得到，包絡信號可由瞬時幅值的乘積得到，而瞬時頻率可由純調頻信號求得，因此LMD方法可自適應將多分量信號自適應分解為若干個單分量的調幅-調頻信號[9],鑒于齒輪振動信號具有的多分量耦合特性，LMD是其理想的信號分析方法。

針對齒輪振動信號的強背景噪聲和多分量耦合特性，提出一種基于CBSR消噪和Hermite插值的LMD齒輪故障研究方法。該方法利用CBSR系統將高頻噪聲能量逐級向低頻故障特征轉移，可有效降低高頻噪聲對LMD分解的影響，同時借助Hermite插值作為極值點包絡線擬合方法，得到更精確的包絡估計函數，從而實現對含噪信號的準確分解。通過仿真信號驗證該方法的有效性，并將其應用到齒輪箱振動信號的故障診斷中。

1基于CBSR消噪和Hermite插值的LMD方法

LMD作為一種新時頻分析方法，具有良好的非線性、非平穩信號分析能力，已在機械故障診斷領域得到了廣泛應用。但是由于實際振動信號中往往夾雜大量噪聲，LMD在進行由高頻到低頻自適應分解時，由于受到噪聲影響，得到的PF分量數目增加，產生冗余分量，嚴重時會導致不收斂。當噪聲較大，而故障調制信號微弱時，LMD分解會致使故障信號與噪聲信號的混疊，難以提取故障特征，甚至會導致信號的突變，導致分解結果嚴重失真，影響了LMD分解的準確性。

由于LMD存在上述問題，因此在進行分解時需要對信號進行降噪預處理，文獻[10]提出了小波包降噪和LMD相結合的方法，即首先使用小波包進行降噪處理，后進行LMD分解。但由于小波降噪實質是通過抑制噪聲的方式來提高信噪比，當噪聲頻率與故障特征頻率相近時，在削弱噪聲的同時會削弱故障信息，使得故障信號難以提取[11]。本文提出基于CBSR消噪與LMD相結合的方法，CBSR能夠逐級削弱噪聲，同時加強弱故障信號，相比于小波包降噪更加適用于弱故障信號的特征提取。將信號經過CBSR處理，降低噪聲對LMD的影響，提高LMD分解質量。

1.1級聯雙穩隨機共振理論

(1)隨機共振基本原理

雙穩隨機共振系統[12]是指小周期信號驅動下，系統輸出不能發生躍遷，只能在一個穩態上，而當在弱噪聲和小周期信號共同作用下，隨著噪聲強度的增加，當兩者達到最佳匹配關系時，系統輸出發生躍遷，輸出信號放大最明顯。雙穩隨機共振系統如圖1所示：

圖1　雙穩隨機共振系統 Fig.1 Bistable stochastic resonance system

隨機共振系統由3個不可缺少的因素組成：非線性系統、周期信號s(t)和噪聲信號n(t)，通常用非線性郎之萬方程(Langevin)來描述雙穩態系統：

(1)

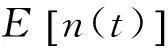
E[n(t)n(t′)]=2Dδ(t-t′)

(2)

式中:D為噪聲強度，δ(t)為沖擊函數。

當A=D=0時，即沒有外部周期驅動力和噪聲，由上式聯立得出勢陷阱方程為：

(3)

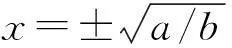
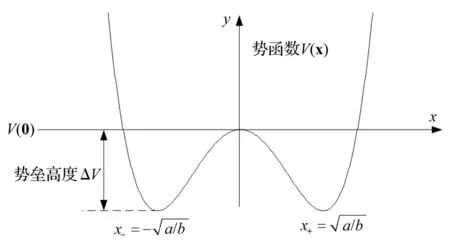
圖2　雙穩系統勢陷阱圖 Fig.2 Bistable system potential pitfalls diagram

實際采樣過程中，采樣頻率一般設置較高，不滿足隨機共振的絕熱近似理論小參數的要求[11]。本文采用二次采樣的方法，首先對大參數信號進行重新采樣，從高頻到低頻進行線性壓縮，使其變為小參數信號，將小參數信號輸入隨機共振系統進行共振處理，然后將處理完的數據按照壓縮尺度還原為大參數信號，使得隨機共振在大參數下得以應用。

(2)CBSR系統

CBSR系統是將單個雙穩隨機共振系統前后進行串聯得到，流程如圖3所示。通過雙穩隨機共振系統的輸出信號，具有洛倫茲分布的特性，即高頻譜能量被逐級遞減，低頻譜能量則被加強。圖4(a)是含噪聲的兩正弦信號的疊加，頻率分別為f1=20 Hz，f2=400 Hz，在圖4(b)中可以清楚的看到兩個特征頻率。圖4(c)、(e)和(g)是經1級、2級和3級CBSR系統輸出后的時域波形圖，其相對應的頻譜圖為圖4(d)、(f)和(h)，將圖

4(b)與圖4(d)、(f)和(h)相對比，發現高頻譜能量被逐級遞減，低頻譜能量則被加強。將圖4(a)與(c)、(e)和(g)相對比，發現隨著級聯級數的增加，高頻成分被逐級濾除，在時域上呈現為輸出波形變得逐漸光滑，提高信噪比的同時達到了對信號的整形。

圖3　CBSR系統 Fig.3 CBSR system

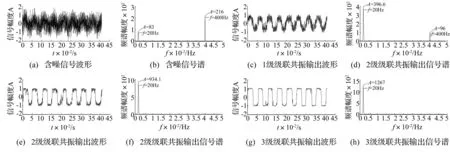
圖4　含噪信號級聯雙穩隨機共振輸出 Fig.4 Noisy signals and CBSR output

1.2基于Hermite插值的LMD算法

LMD分析方法的本質是從原始信號中分離出一個純調頻信號和一個包絡信號,將該純調頻信號和包絡信號相乘便可以得到一個單分量的PF,將具有物理意義的PF分量從原始信號中分離出來并進入下一次迭代，循環處理至所有的PF分量被分離出來，剩余一單調函數為止。其中PF分量的幅值為對應包絡函數，瞬時頻率由純調頻信號sin(t)通過式(4)求出。

(4)

LMD在分解過程中，局部均值函數m(t)和包絡估計函數a(t)都是采用滑動平均法獲得，由于滑動平均法在平滑處理過程中會產生相位誤差，導致局部均值函數m(t)和包絡估計函數a(t)的失真，影響了LMD分解結果的準確性。三次樣條(spline)插值法[13]可有效解決上述問題，但因其在節點處具有二階導數連續的特性，對于非光滑信號會產生過包絡和欠包絡現象。標準三次 Hermite 插值法是一種工程中廣泛應用的插值曲線構造方法，相比于三次樣條插值，它構造的曲線僅要求節點處一階導數連續，這樣既能保證各點的連續性和平滑性又使其具有優良的保形特性，更適合于具有非平穩非線性的齒輪箱振動信號的包絡擬合。因此本文采用Hermite插值的方法構造包絡線，首先利用Hermite插值函數分別擬合信號的局部極大值點和局部極小值點，獲得信號的上包絡線Eup(t)和下包絡線Elow(t)，然后局部均值函數m(t)由式(5)求得，包絡估計函數a(t) 由式(6)求得。

(5)

(6)

完成局部均值函數m(t)和包絡估計函數a(t)后，則按照LMD原方法循環求解各PF分量，直至循環結束。

1.3基于CBSR消噪和Hermite插值的LMD方法的算法流程

該算法首先將含噪信號輸入CBSR系統降噪，然后將共振輸出信號進行LMD分解，提高其分解質量，具體步驟如下：

(1)將原始含噪信號x(t)進行二次采樣使其滿足隨機共振絕熱小參數的要求。

(2)將小參數信號輸入CBSR系統進行降噪得到xn(t)。

(3)將xn(t)還原為原始信號采樣頻率。

(4)計算得出原始信號xn(t)的極值點序列nk，對其進行端點延拓，得到新的極值點序列Xk。

(5)從極值點序列Xk一端開始，選取局部相鄰的極大(或小)值點，利用Hermite插值法進行連線，生成上下包絡線，分別記為Eup(t)和Elow(t)。

(6)利用式(5)和式(6)計算得到局部均值函數m(t)和包絡估計函數a(t)。

得到局部均值函數和包絡估計函數后，繼續執行LMD的后續步驟即可以實現基于CBSR消噪和Hermite插值的LMD的算法，算法流程見圖5所示。

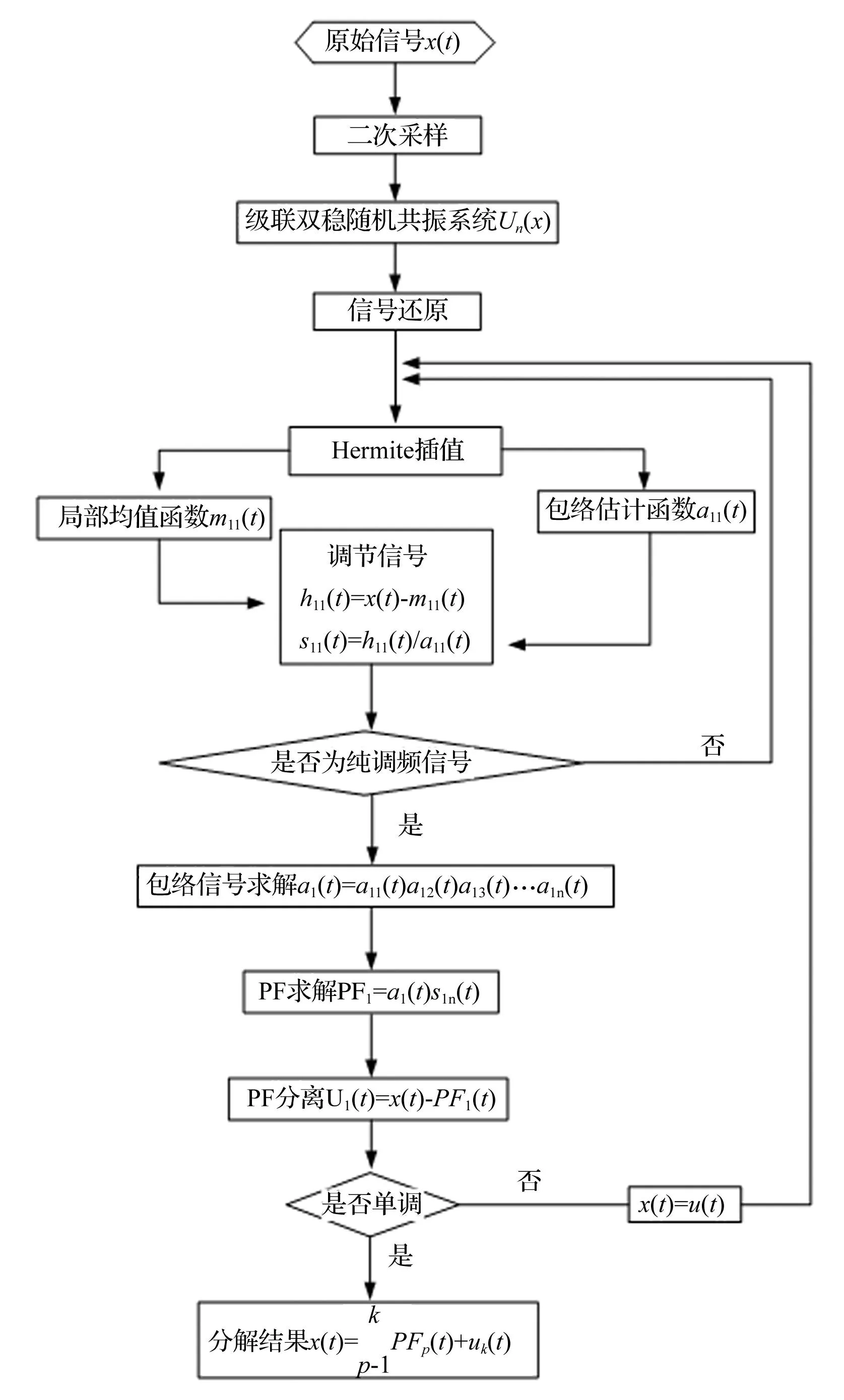
圖5　基于CBSR消噪和Hermite插值的LMD算法流程圖 Fig.5 Flow chart of the CBSR denoising and Hermite interpolation LMD

2仿真數據試驗

為了說明經CBSR系統降噪處理后可提高LMD的分解質量，本文選取仿真信號x(t)的表達式為：

該仿真信號由一個調幅信號x1(t)和一個調頻信號x2(t)組成，同時摻雜有白噪聲，設定采樣頻率為1 000Hz,采樣點數為2 048。

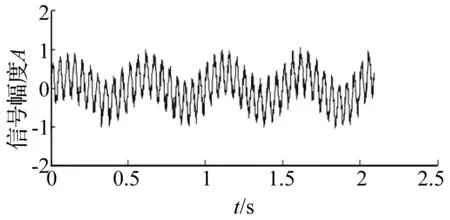
圖6　含噪信號的時域波形 Fig.6 Waveforms of noisy signal

為了說明級聯雙穩隨機共振和Hermite-LMD方法的優越性，分別同小波降噪和spline-LMD方法、級聯隨機共振和spline-LMD方法進行對比，三種方法均以鏡像延拓法降低端點效應的影響，迭代終止條件誤差設置為10-4。設定二次采樣頻率為5 Hz, 隨機共振參數a=0.1，b=1，采用2級隨機共振降噪。三種方法的分解結果如圖7、圖8和圖9所示。

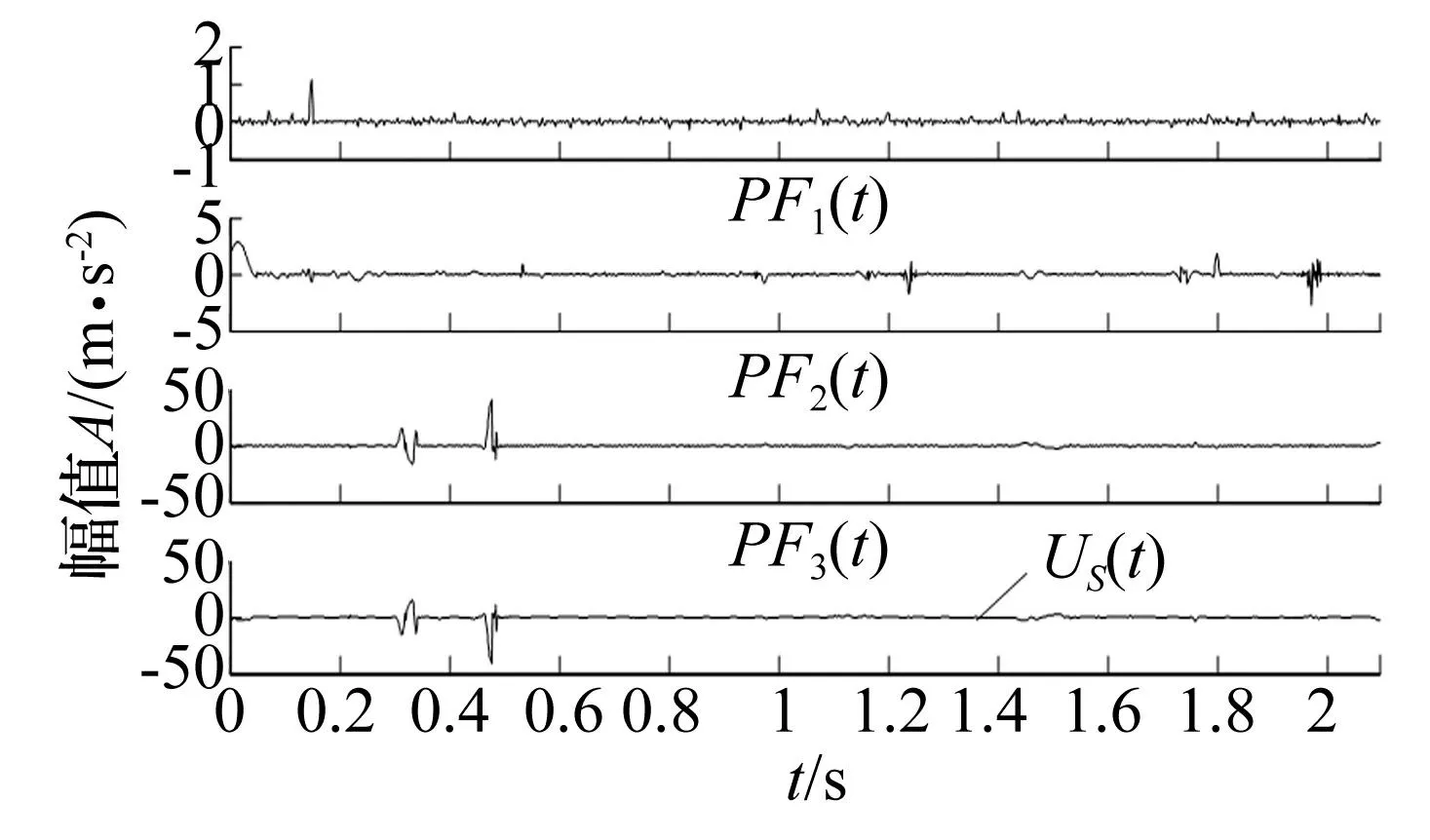
圖7　小波降噪輸出后spline-LMD分解結果 Fig.7 spline-LMD results of the wavelet denoising output

圖7是原信號進行小波降噪后的spline-LMD分解結果，從圖中可以看出，分解的結果嚴重失真，失去分解的物理意義。

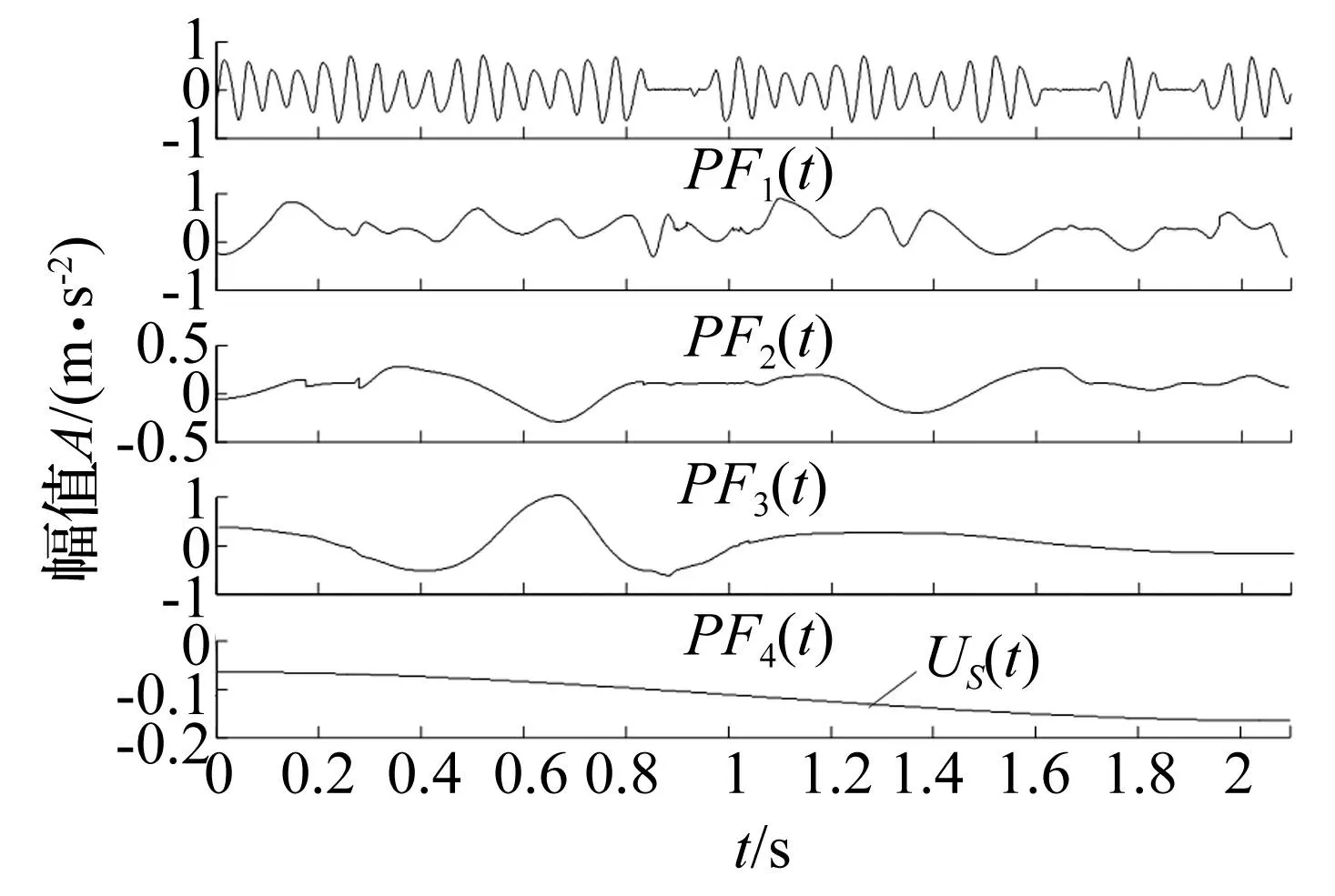
圖8　級聯隨機共振輸出后spline-LMD分解結果 Fig.8 Spline-LMD results of the CBSR output

圖8和圖9是原信號進行2級CBSR降噪后的spline-LMD和Hermite-LMD分解結果，從圖8中可看出經CBSR處理后spline-LMD分解為5個PF分量和一個殘余分量，高頻成分有所減少，未見高頻分量，其中PF1分量對應調頻信號x2(t),PF2分量對應調幅信號x1(t)，雖然都存在局部失真，但較圖7已有較大改進。圖9中可看出Hermite-LMD分解為三個PF分量和一個殘余分量，高頻成分基本濾除，能夠清晰地找出調頻信號x2(t)和調幅信號x1(t)(分別對應PF1分量和PF2分量)，能夠較準確分解出有效成分。與圖7對比發現，經過CBSR處理后， LMD的分解層數減少，分解的準確度明顯提高，優于其他兩種方法分解的結果。

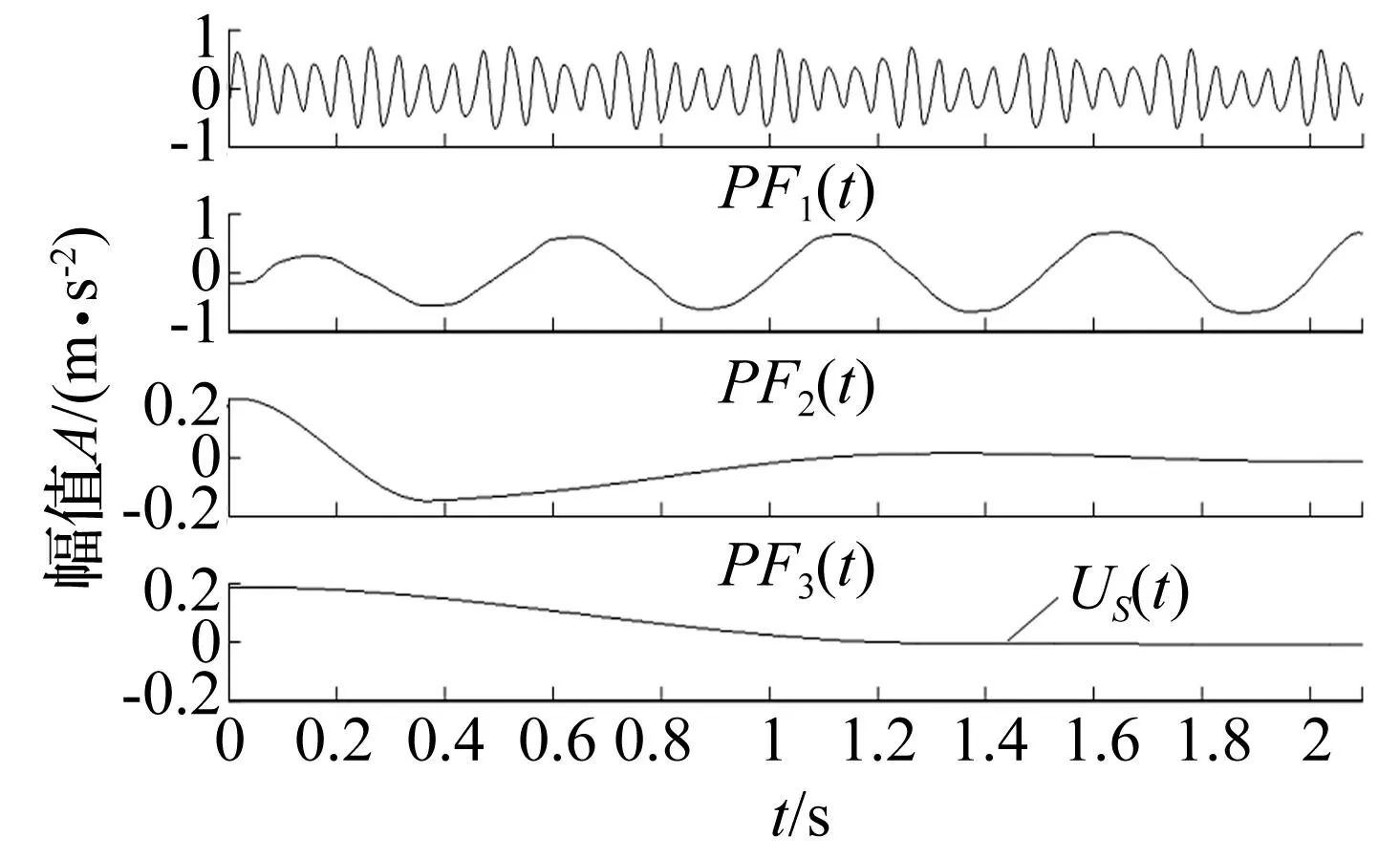
圖9　級聯隨機共振輸出后Hermite-LMD分解結果 Fig.9 Hermite-LMD results of the CBSR output

3齒輪磨損故障診斷實例

本文中采用的試驗臺是江蘇千鵬旋轉機械振動故障試驗平臺，如圖10(a)所示，該試驗臺可變速模擬在不同轉速條件下的故障特征，其型號為QPZZ-Ⅱ，該試驗臺的組成為：電力驅動系統、齒輪箱及磁粉制動器。電力驅動系統為變頻異步電動機，其調速范圍是0~1 500 r/min；本實驗臺所用的齒輪箱從輸入端到輸出端只有一對齒輪嚙合形成單級傳動，即為一級齒輪箱，具有減速的特性，表1為齒輪的幾何參數。通過磁粉制動器模擬齒輪箱工作負載，其型號為CZ-0.5，額定轉矩為5N·M。小齒輪的轉速為1 500 r/min,由此可得齒輪的嚙合頻率為fm=1 375 Hz, 大齒輪軸的轉動頻率為f1=18.33 Hz，小齒輪軸的轉動頻率為f2=25 Hz，設定采樣頻率為fs=10 000 Hz。

表1　齒輪箱齒輪的幾何參數

圖10　機械振動故障試驗平臺 Fig.10 The fault experiment platform of mechanical vibration

本試驗臺所用故障件是齒輪箱中的大齒輪，在試驗過程中，利用已磨損的齒輪，模擬齒輪箱傳動機構長期使用的磨損故障。在輪齒齒面兩側各磨0.1 mm，其故障注入部位如圖10(b)所示。

根據齒輪箱的結構特點，在齒輪箱軸承底座處故障敏感部位設置了測點，利用加速度傳感器測試齒輪箱振動信號，振動信號的時域波形如圖11所示。

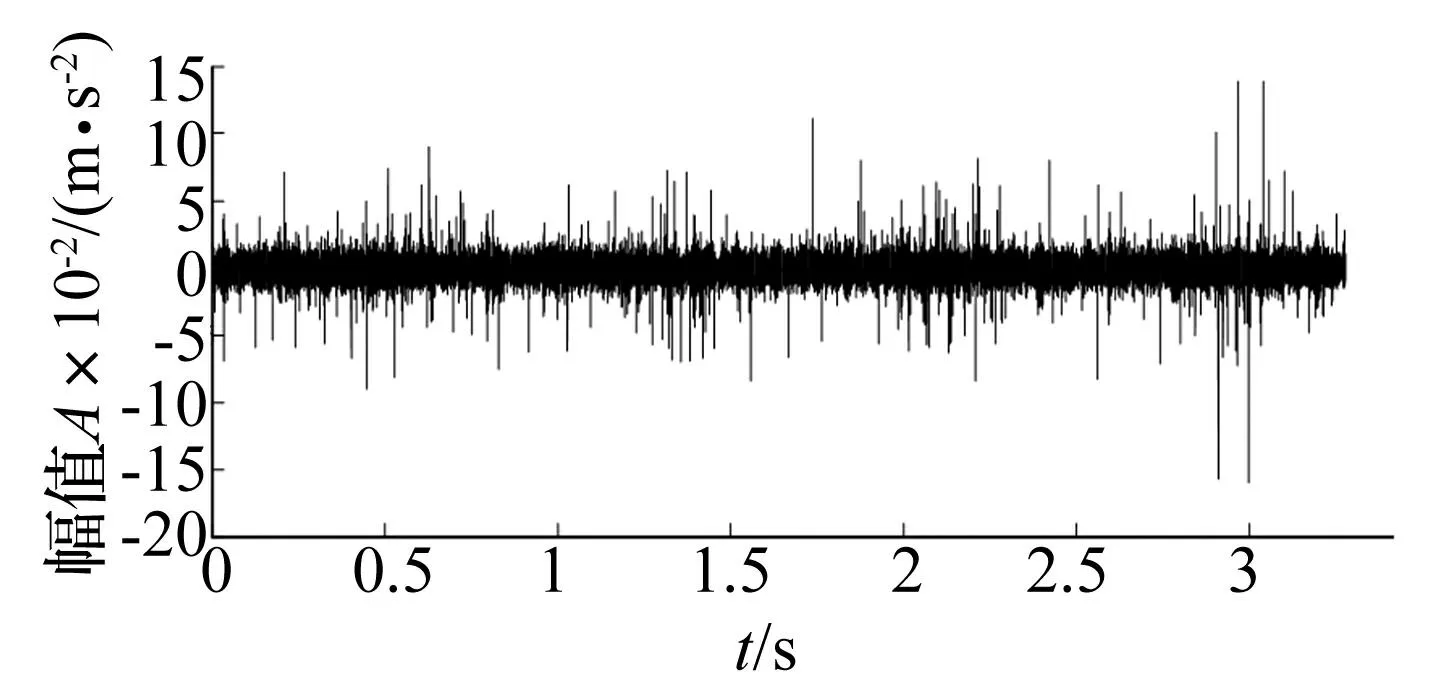
圖11　齒輪箱輕度故障的加速度信號 Fig.11 The acceleration signal of gear with tiny faults

在齒輪故障診斷中，齒輪的故障振動信號是以齒輪箱系統的共振頻率為載波頻率，以齒輪故障特征頻率為調制頻率的調幅信號，由于內部運動部件較多，實測信號可認為是由多個調幅信號耦合而成。因此，齒輪箱的振動信號是典型的非平穩多分量信號，適合用LMD方法進行分解。當齒輪存在局部磨損故障時，在嚙合時會產生沖擊振動，其信號的幅值和相位發生變化，產生幅值和相位調制，在頻域上產生以嚙合頻率為中心以磨損軸轉頻為間隔的調制邊頻帶，通過對邊頻帶識別可以對齒輪故障進行診斷。而當齒輪出現斷齒故障時，其邊頻帶變現為數量較多、幅值較大、分布較寬。當齒輪出現點蝕故障時，其邊頻帶數量稀少且分布稀少。

為驗證本文提出方法對齒輪箱故障特征的提取能力的優越性，分別采用基于小波降噪和spline-LMD、基于CBSR降噪和spline-LMD和基于CBSR降噪和Hermite-LMD的方法對故障信號進行分解。分解過程中以鏡像延拓法降低端點效應，迭代終止條件的誤差設置為10-3，采用2級CBSR系統降噪，參數設置如下：二次采樣頻率為10 Hz,a=1，b=1，進行2級降噪。由于分解結果中的前幾個PF分量包含了設備狀態的主要信息，所以僅給出了各種方法分解結果的前四個PF分量，分別如圖12~圖14所示。

圖12是三次樣條(spline)插值法的分解結果，發現PF3分量在0.5至1 s時間段產生了突變，無法繼續分解，而另兩種方法能順利完成分解，說明了隨機共振降噪相比于小波降噪的優越性。

為說明Hermite插值形成包絡線的優越性，截取分解過程中0.005-0.007 s時間段信號進行對比，如圖15所示。其中三次樣條插值的構成的上下包絡線為實

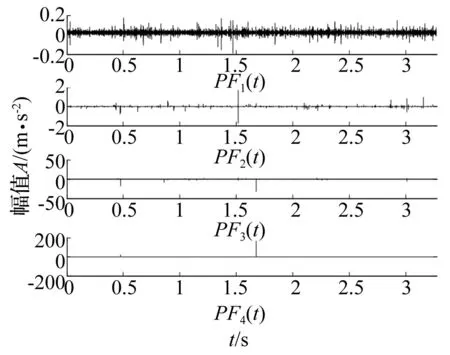
圖12　小波降噪后進行spline-LMD法的分解結果 Fig.12 Spline-LMD decomposition results of the wavelet deniosing output

圖13　級聯隨機共振輸出后spline-LMD法的分解結果 Fig.13 Spline-LMD decomposition results of the CBSR output

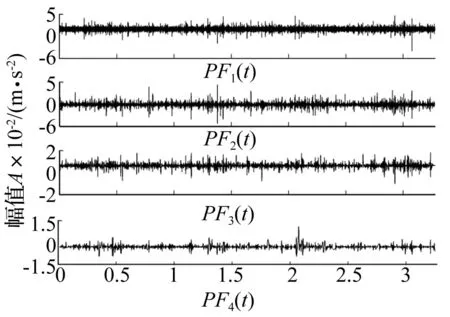
圖14　級聯雙穩隨機共振輸出 Hermite-LMD法的分解結果 Fig.14 Hermite-LMD decomposition results of the CBSR output

線，從圖中發現有明顯的過包絡現象，從而導致LMD分解結果失真。同樣應用Hermite插值法對該段信號進行上下包絡，如圖15中虛線所示，發現采用Hermite插值較好避免了過包絡現象，對信號包絡較好，說明了Hermite插值法對非平穩信號具有良好的適應性。

圖15　三次樣條和Hermite插值的包絡結果 Fig.15 The envelopes of the cubic spline and Hermite interpolation

由于齒輪故障信號激起的共振頻率多分布在信號的高頻段，調制頻率分布于低頻段。因此，進一步對PF(t)分量的瞬時幅值a(t)做FFT變換，得到瞬時幅值的幅值譜，進行頻譜分析，可得出齒輪箱內部運動部件的激勵頻率，以此評定設備運行狀態。分別對基于小波降噪和spline-LMD、基于CBSR消噪和spline-LMD和基于CBSR消噪和Hermite-LMD的方法的第一個PF分量的瞬時幅值進行頻譜分析，頻譜圖如圖12和圖13所示。

由圖16可知，在基于小波降噪和spline-LMD方法的頻譜中沒有找到故障頻率(即故障齒輪的轉動頻率為f1=18.33 Hz)，而在基于CBSR降噪和spline-LMD、基于CBSR降噪和Hermite-LMD方法的頻譜中在故障頻率處均出現了峰值，說明信號經CBSR系統處理后，故障調制信號被加強，噪聲信號被減小，提高了信號的信噪比，然后經LMD分解后能夠發現故障信息。驗證了CBSR降噪和LMD方法應用于齒輪故障診斷的有效性，相比于小波降噪方法，它能夠更加準確的捕捉到故障微弱特征，并提高LMD分解的質量。

圖16 基于小波和spline-LMD方法的PF1分量幅值頻譜Fig.16TheamplitudespectrumsofthePF1componentsofwaveletandspline-LMDmethod圖17 基于CBSR和spline-LMD方法的PF1分量幅值頻譜Fig.17TheamplitudespectrumsofthePF1componentsofCBSRandspline-LMDmethod圖18 基于CBSR和Hermite-LMD方法的PF1分量幅值頻譜Fig.18TheamplitudespectrumsofthePF1componentsofCBSRandHermite-LMDmethod

對比圖17和18可以發現，三次樣條插值法中，故障頻率周邊有較多峰值干擾，故障頻率不明顯，而Hermite插值法比三次樣條插值法的故障頻率以及其它倍頻的峰值更加顯著。為了進一步說明本文提出方法的有效性，將兩種方法的幅值頻譜進行歸一化對比，如圖19所示。可以看出，spline-LMD方法的故障頻率幅值明顯低于Hermite-LMD方法且在故障頻率的二倍頻處沒有峰值。因此，基于CBSR消噪和Hermite插值LMD方法可以更加準確地診斷出齒輪磨損的早期故障。

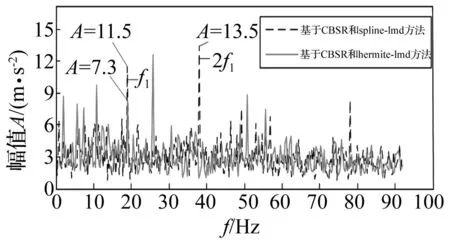
圖19　級聯雙穩隨機共振輸出后 spline-LMD和Hermite-LMD的幅值譜 Fig.19 The amplitude spectrum of the spline-LMD and Hermite-LMD method after the CBSR output

4結論

提出了CBSR與基于Hermite插值的局部均值分解相結合齒輪故障診斷的方法。

(1)針對強背景噪聲下，直接采用LMD法難以提取弱的故障特征，提出將信號進行CBSR降噪處理后進行LMD分解的方法，CBSR系統基于非線性低通濾波原理，將高頻噪聲能量逐級向低頻故障特征轉移，降低高頻噪聲對LMD分解的影響，提高LMD分解的準確性；

(2)給出了CBSR消噪與LMD分解相結合的算法流程，并通過仿真數據試驗驗證了該方法優越性；

(3)以齒輪箱齒輪故障振動信號為對象，驗證了該方法對弱故障信號提取的有效性，實現了齒輪箱早期磨損故障的準確診斷。

此外，在CBSR中二次采樣頻率取值范圍的確定仍無理論依據，還有待進一步研究。

參考文獻

[1]畢果,陳進. 基于譜相關的齒輪振動監測技術研究[J].振動與沖擊, 2009, 28(7): 17-21.

BI Guo,CHEN Jin. The study of gear vibration based on the Spectrum[J]. Journal of Vibration and Shock，2009, 28(7): 17-21.

[2]Benzi R，Sutera A，Vulpiani A. The mechanism of stochastic resonance[J]. Journal of Physics A ：Mathematical and General，1981，14：453-457.

[3]趙艷菊，王太勇,冷永剛,等. 級聯雙穩隨機共振降噪下的經驗模式分解[J]. 天津大學學報, 2009, 42(2): 123-128.

ZHAO Yan-ju, WANG Tai-yong，LENG Yong-gang.Empirical mode decomposition based on cascaded bistable stochastic resonance denoising[J]. Journal of Tianjin University, 2009, 42(2): 123-128.

[4]Cohen L. Time-frequency distribution-areview[J].Proceedings of the IEEE, 1989, 77(7): 941-981.

[5]壽海飛. 基于小波分析的齒輪故障診斷研究[D].杭州.浙江工業大學，2007.

[6]Huang N，Long S R． A new view of nonlinear water wave: the Hilbert spectrum[J]． Ann． Rev． Fluid Mech． 1999，31: 417-57.

[7]王衍學，何正嘉，訾艷陽，等. 基于LMD的時頻分析方法及其機械故障診斷應用研究[J]．振動與沖擊，2012，31(9): 9-12.

WANG Yan-xue,HE Zheng-jia,ZI Yan-yang. Several key issues of local mean decomposition method used in mechanical fault diagnosis[J]．Journal of Vibration and Shock，2012，31(9): 9-12.

[8]Smith J S. The localmean decomposition and its ap-plication to EEG perception data[J]. Journal of the Royal Society Interface, 2005, 2(5): 444-450.

[9]程軍圣，張亢，楊宇. 局部均值分解與經驗模式分解的對比研究[J].振動與沖擊，2009，28(5): 13 -16.

CHENG Jun-sheng，ZHANG Kang, YANG Yu. The comparison of the local mean decomposition method and the empirical mode decomposition method[J]. Journal of Vibration and Shock，2009，28(5): 13-16.

[10]孫偉，熊邦書,黃建平,等. 小波包降噪與 LMD 相結合的滾動軸承故障診斷方法[J]. 振動與沖擊, 2012, 31(18): 153-156.

SUN Wei, XIONG Bang-shu,HUANG Jian-ping.Fault diagnosis of a rolling bearing using Wavelet packet de-noising and LMD[J]. Journal of Vibration and Shock, 2012, 31(18): 153-156.

[11]冷永剛, 王太勇. 二次采樣用于隨機共振從強噪聲中提取弱信號的數值研究[J]. 物理學報, 2003, 52(10): 2432-2437.

LENG Yong-gang,WANG Tai-yong. The study of two sampling used to extraction of weak signal from strong noise [J]. Acta Physica Sinica, 2003, 52(10): 2432-2437.

[12]雷亞國，韓東，林京．自適應隨機共振新方法及其在故障診斷中的應用[J]．機械工程學報，2012，48(7): 62-67.

LEI Ya-guo, HAN Dong，LIN Jing. New adaptive stochastic resonance method and its application to fault diagnosis[J]. Journal of Mechanical Engineering, 2012，48(7): 62-67.

[13]張亢, 程軍圣, 楊宇. 基于有理樣條函數的局部均值分解方法及其應用[J]. 振動工程學報, 2011, 24(1): 97-103.

ZHANG Kang, CHENG Jun-sheng，YANG Yu. The local mean decomposition method based on rational spline and its application[J]. Journal of Vibration Engineering, 2009, 2011, 24(1): 97-103.