基于 FE-SEA 混合法的空心阻振質量阻振性能研究

第一作者溫華兵男，副教授，1977年生

基于FE-SEA混合法的空心阻振質量阻振性能研究

溫華兵，彭子龍，劉林波

(江蘇科技大學振動噪聲研究所，江蘇鎮江212003)

摘要：闡述了FE-SEA混合法的基本原理，分別采用FEM、SEA和FE-SEA混合法對帶阻振質量薄板結構的振動速度進行預測。通過設計帶近似等質量的空心梁與實心梁阻振質量的薄板結構模型實驗，對上述三種方法的預測結果進行了驗證。通過定義特征尺寸與波長的比值△，找到了各自的控制頻域。結果表明：采用Δ作為劃分上述三種方法有效頻域的指標是可行的；在分析頻率8 kHz范圍內，空心阻振質量比實心阻振質量的整體阻振效果提高了10 dB左右；尤其是在中高頻區的阻振效果更加明顯，但在100 Hz以下的低頻區阻振效果不如實心阻振質量的好。說明空心阻振質量比實心阻振質量具有更好的應用前景。

關鍵詞：FE-SEA混合法；空心方鋼；實心方鋼；阻振質量；傳遞損失；速度響應；特征尺寸

基金項目：國家自然科學

收稿日期：2013-11-08修改稿收到日期：2014-03-07

中圖分類號:TB532文獻標志碼：A

Vibration-isolating performance of hollow-square-steel blocking mass based on hybrid FE-SEA method

WENHua-bing,PENGZi-long,LIULin-bo(Institute of Noise and Vibration, Jiangsu University of Science and Technology, Zhenjiang 212003, China)

Abstract:The basic principle of the FE-SEA hybrid method was presented, and a plate structure model with blocking masses was built based on FEM, SEA and FE-SEA hybrid method, separately. By performing the model tests of plate structures with approximate equal-mass hollow beam and solid beam, the predicted results with the above three different methods were verified using tests. Defining a parameter △ to indicate the ratio of characteristic dimension to wavelength, and according to △, the whole frequency range was divided into some parts, the governing frequency ranges suitable for each analysis method were found. The results showed that the method of adopting the parameter △as the index of distinguishing effective frequency ranges is feasible; within the range of 8 kHz, the vibration-isolating performance of the whole structure with hollow blocking mass is nearly 10dB higher than that with solid blocking mass, especially, in mid-high frequency range the vibration-isolating effect is much obvious; however, the vibration-isolating performance of the structure with hollow blocking mass is worse compared with that with solid blocking mass within the frequency range below 125Hz; the hollow blocking mass has a better application prospect than the solid blocking mass does.

Key words:hybrid FE-SEA method; hollow-square steel; solid-square steel; blocking mass; transmission loss; velocity response; characteristic dimension

傳統的分析復雜結構振動與聲輻射的方法主要有確定性分析方法和統計性分析方法兩大類。前者以有限元法(FEM)為主，它吸取了差分法對求解域進行離散處理的啟發，又繼承了里茲法選擇試探函數的合理方法，使得處理的問題更為復雜，因而得到廣泛的應用。但是隨著分析頻率的提高并且為了滿足每個波長內6～10個單元的原則，使得網格急劇增加，計算成本加大。并且有限元模型的建立是基于系統的確定性物理參數，實際的結構在制造和裝配過程中不可避免產生公差，而系統在高頻區對參數微小變化異常敏感，導致計算產生嚴重失真。

而統計性分析方法目前主要是統計能量法(SEA)，它從時間、頻率、空間平均的統計角度預測子系統間的能量流傳遞、各子系統的能量響應。但是其理論前提對于模態密集的高頻振動是合理的，這就使得該方法在有效分析頻率上受到限制。

尤其當復雜結構在中頻區內承受來自外界的振動與噪聲載荷時，模態密度存在較大差異的結構呈現出復雜的力學特性。單純采用FEM或SEA都無法解決這類問題[1]。為此，Langley等[2-3]分別創立了基于模態耦合和波動理論的FE-SEA混合法，從而使復雜結構全頻段的振動與聲輻射問題的解決成為可能。

基于阻抗失配機理，阻振質量常常被布設在板的結合處，使結構中傳遞的振動波受到部分反射，從而達到隔聲的目的。車馳東等[4]基于波動理論研究了多轉角阻振質量結構對結構聲的阻抑特性。王獻忠等[5]采用FE-SEA混合法求解含阻振質量基座的聲振響應問題，并進行了雙層殼模型實驗研究。申華等[6]在實心方鋼阻振的理論基礎上，研究了平板結構受點激勵時空心方鋼阻振質量對結構中振動波傳遞的阻抑特性。

對于不同截面形狀的阻振質量的阻振性能目前研究仍然較少，如何使阻振質量既滿足有較好的阻振效果又能節省材料成為阻振質量進一步研究的問題。由于阻振質量和板殼結構之間的模態密度存在較大差異，尤其當所構成的結構較為復雜時，采用波分析法的解析較為困難，單一使用FEM或SEA所建立的模型也不能用于寬頻范圍的振動特性分析。分別采用FEM、SEA和FE-SEA混合法研究了近似等質量的空心阻振質量與實心阻振質量的薄板結構的阻振特性，并通過實驗進行了驗證。

1基于波動理論的FE-SEA混合法基本原理[3]

1.1系統整體運動方程

類比有限元頻響分析，經傅里葉變換FE-SEA混合法中系統的動力學方程為

(1)

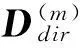
(2)

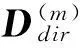
(3)

式中:〈Sqq〉為確定性子系統中節點的位移響應：

(4)

符號·-H表示矩陣的共軛轉置并求逆的運算。

1.2直接場與混響場的互易關系

隨著隨機邊界上的不確定性因素的增加，方程(4)里面混響場受擋力f(m)rev趨近下面的極限

(5)

式中:αm為與混響場振幅相關的比例常數。

(6)

式中:Em和nm分別為第m個隨機子系統在混響場中所具有的能量和第m個隨機子系統的模態密度。

1.3混合連接的功率平衡方程

如圖1所示，對于與確定性子系統相連的第m個隨機子系統，在混合連接處存在以下功率平衡方程

(7)

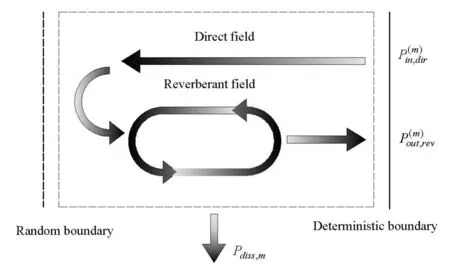
圖1　隨機子系統中功率平衡示意圖 Fig.1 Schematic representation of energy flow balance within a statistical subsystem

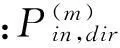
(8)

式中:

(9)

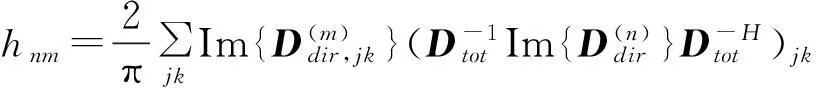
(10)

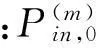
(11)

式中:htot,m為第m個隨機性子系統在混響場中的能量損耗系數：

(12)

而Pdiss,m可表示為

Pdiss,m=ωηmEm

(13)

式中:ηm為第m個隨機子系統的內損耗因子。

將式(8)～(13)代入式(7)，即可對隨機性子系統的響應進行求解。然后根據互易關系，即式(5)～(6)得到作用在確定性子系統上的力譜。最后根據(1)～(4)建立系統整體動力學方程，求解確定性廣義坐標下的集合平均值〈Sqq〉，每個頻率重復進行。

新時期，新發展，十八大以來，我國進入了全面深化改革的新的歷史時期，鄉村振興戰略規劃出了新時期農業農村工作的發展路徑，農業不斷向著綠色、現代化邁進。與時代同步，面對深化改革和綠色發展的新要求，化肥流通行業也在不斷轉型升級，開創出了創新融合發展的新格局，有力推動了化肥工業的供給結構性側改革，為新時代的新農業發展提供了有力的支持。

2數值計算

按照上述基本原理，建立帶近似等質量的空心梁與實心梁板結構的混合法模型，其結構示意圖見圖2。板A～F為邊長0.5 m厚度3 mm的正方形鋼板，密度7 800 kg/m3，泊松比為0.3，彈性模量為2.1×1011Pa。為了產生入射的平面彎曲波，在A板、B板間加裝了一根大剛度實心方形截面梁(以下簡稱中間梁)，并在中間位置施加一隨機激勵力，其大小可由下文的實驗測得，如圖3所示；在A板、C板間布置實心阻振質量(尺

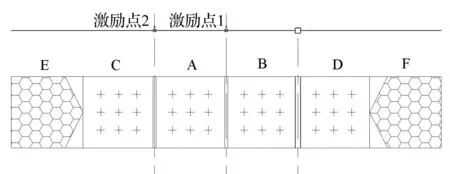
圖2　帶阻振質量薄板結構模型 Fig.2 Sheet structure model with blocking masses

寸同中間梁)，在B板、D板間布置空心阻振質量，其參數如表1所示。為了吸收E板與F板邊緣的反射波，以模擬半無限長的情況，在E板與F板的上下表面和端部粘貼了5 mm厚粘彈性阻尼材料，其密度為1 000 kg/m3，泊松比0.49。計算時各板、阻振質量、阻尼材料的內損耗因子均來自下文的實驗測量，如圖4所示。

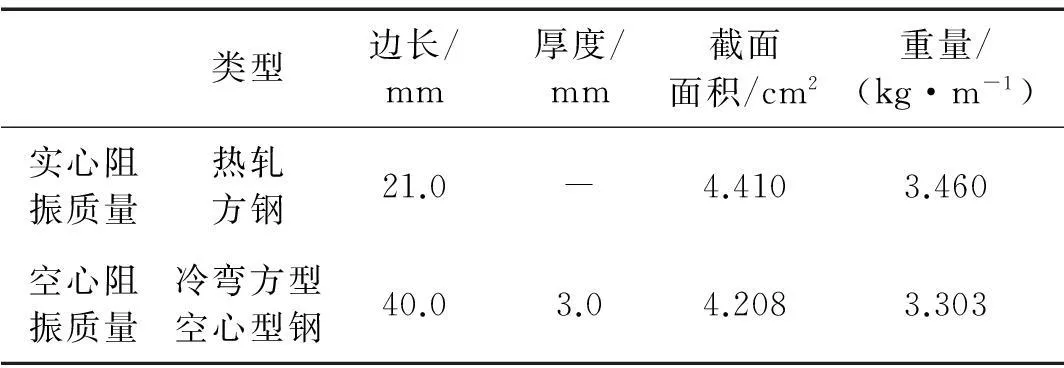
表1　阻振質量參數

考慮到FE-SEA混合法中子系統的劃分與波長的內在聯系，有必要對結構中波長隨頻率的變化情況進行分析。并且由于薄板中彎曲波長通常遠小于拉伸和剪切方向的波長，模型中的薄板又以彎曲為主，所以只考慮彎曲波即可。薄板或梁中彎曲波長可表示為[7]：

(14)

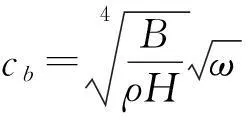
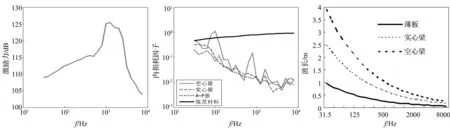
圖3 激振力頻譜圖Fig.3Excitingforcespectrogram圖4 內損耗因子Fig.4Dampinglossfactor圖5 結構中的彎曲波長Fig.5Structuralbendingwavelength

由于薄板與阻振質量的剛度相差較大，薄板與阻振質量分別采用SEA、FEM建模。并且為了驗證FE-SEA混合法建模的正確性，還分別采用了FEM、SEA在31.5～8 000 Hz頻率范圍內(1/3倍頻程)進行分析。同時，為了找出各自方法的有效頻率區間，本文還定義了特征尺寸D與波長λb的比值這一無量綱數作為判定上述三種方法有效性的指標。

(15)

具體計算結果見后文與實驗測試結果的對比。

3實驗驗證

圖6　實驗現場 Fig.6 Experimental site

為了驗證基于FE-SEA混合法建立模型的正確性，本文還開展了帶阻振質量薄板結構的阻振性能對比實驗研究，實驗現場如圖6所示。實驗時，為了減小板邊緣的反射波的影響以及粘貼阻尼層后結構阻抗突變的影響，阻尼層被布置成圖6中所示的V形狀，試樣由多根彈性繩懸掛以模擬自由邊界條件。

考慮到中間、左側實心梁尺寸、材料完全一樣，且兩次激勵力大小一樣，同時為了消除兩次激勵點輸入阻抗的差異，因此在假定阻尼材料完全吸收邊界反射波的情況下，可以認為激勵點2時單位激振速度下的C板的平均振動速度即為激勵點1時左側實心梁與右側空心梁入射波的大小。從而，可以采用傳遞損失來衡量空心、實心阻振質量的阻振效果。其表達式為：

(15)

式中:R、ω、v分別為傳遞損失、分析圓頻率、對應板的單位激勵速度下的平均振動速度，角標s、h、1、2分別表示實心、空心、激勵點1、激勵點2，上標橫線表示平均值，C、D分別表示C板、D板。

激勵中間梁時不同區域板結構的振動速度實測值(基準值為10-6)如圖7所示，傳遞損失的實測值如圖8所示。

通過對比可見：①位于施加激勵的中間梁兩側的A板與B板的振動速度實測值在4kHz以下差異不明顯，在4kHz以上頻率B板的振動速度比A板高5 dB左右。其原因在于：阻振質量相當于一個“低通濾波器”，在低頻區，空心阻振質量與實心阻振質量對入射波的反射能力差別不大；但在高頻區，空心阻振質量的反射能力逐漸凸顯，使得B板的反射波的能量加強，因而振動速度幅值比A板高。②D板與C板的振動速度在低頻區差異不明顯；但在800 Hz以上中高頻區，振動速度較C板低5 dB左右，尤其在1.25～2.5 kHz頻率范圍內，較C板低10 dB以上；D板的總振動速度比C板低12 dB。③在63 Hz以下的低頻區，實心阻振質量的阻振效果比空心阻振質量的好4 dB左右；在0.16～1.25 kHz以上的中頻區，兩者總體差異不大，但空心阻振質量的阻振效果略好2 dB左右；在高于1.25 kHz的高頻區，兩者的阻振效果逐步加大，尤其在1.25～2.5 kHz頻率范圍內，空心阻振質量的阻振效果比實心的高10 dB左右。

由此發現，空心阻振質量比實心阻振質量在較高頻區的阻振效果更加明顯。其原因可能在于：高頻區空心阻振質量由于其內部結構的差異，對于入射波的反射能力比實心阻振質量好，在中間梁受到同等激勵的情況下，使得D板的振動水平比C板低。

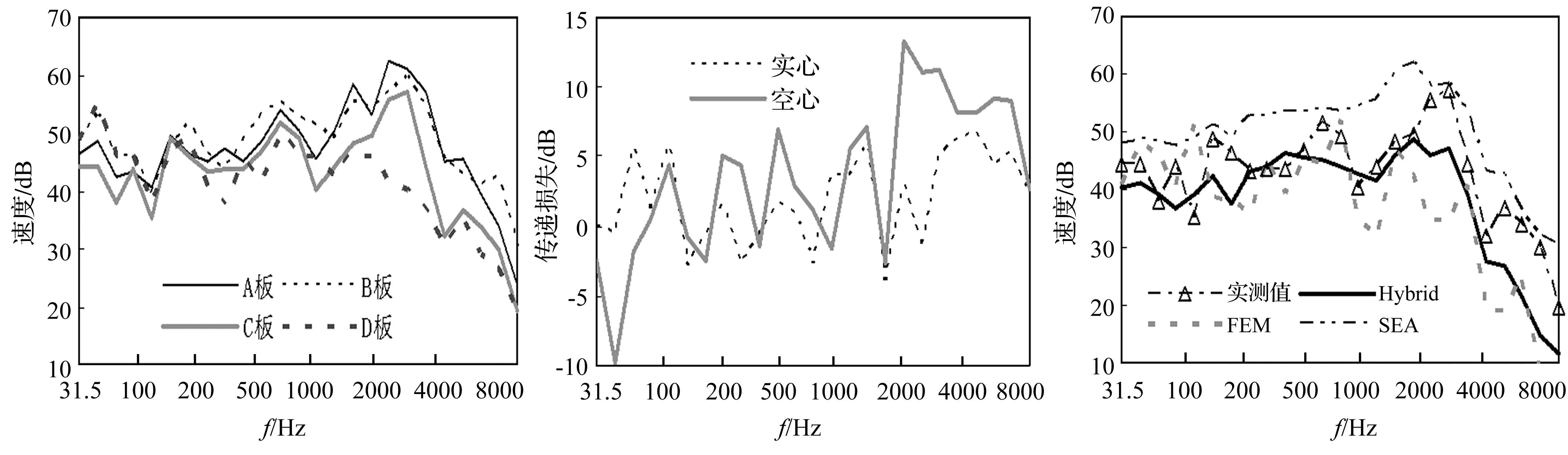
圖7 不同區域的振動速度實測值Fig.7Velocitymeasuredvaluesofdifferentareas圖8 傳遞損失的實測值對比Fig.8Measuredvaluesoftransmissionloss圖9 C板的振動速度比較Fig.9ComparisonofvibrationvelocityofsheetC

分別采用FEM、SEA、FE-SEA混合法對模型進行數值計算，得到C板、D板的振動速度對比結果分別如圖9、圖10所示。由于薄板的特征尺寸為其對角線長0.707 m，空心梁與實心梁的特征尺寸為0.5 m，根據(15)式可得結構的特征尺寸D與波長λb的比值Δ隨頻率的變化曲線如圖11。

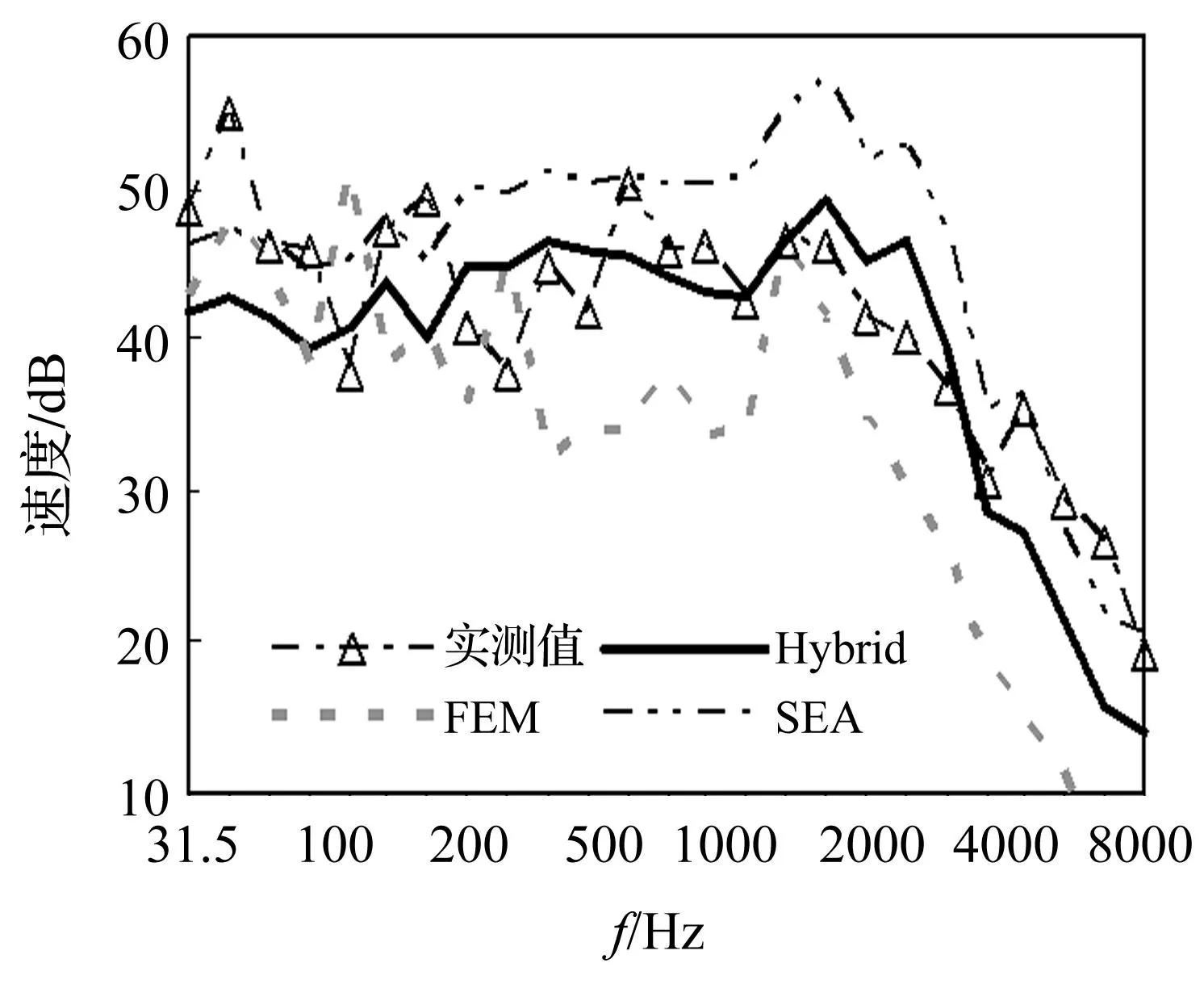
圖10　D板的振動速度比較 Fig.10 Comparison of vibration velocity of sheet D

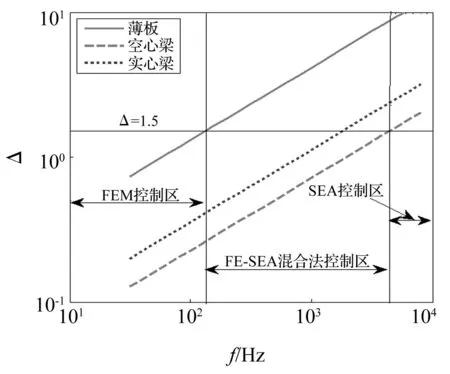
圖11　Δ隨頻率的變化曲線 Fig.11 Variation curves of Δ with infrequency

通過對比發現：

(1)對于C板、D板的振動速度，當頻率低于125 Hz時，其FEM的計算結果與實測值最接近；在0.16～4 kHz的中頻區，FE-SEA的計算結果與實測值最接近；而當頻率高于5 kHz時，SEA的計算結果與實測值最接近。

(2)C板與D板振動速度的FEM計算結果，隨著分析頻率的提高，逐漸偏離實驗值，呈下降趨勢。其主要原因在于有限元在高頻區對結構參數、振動速度載荷的不確定性以及結構制造工藝誤差異常敏感，使得誤差不斷積累。而SEA的計算結果在4 kHz以下，基本上高于實測值，且誤差較大，主要原因在于結構沒有達到較高的模態密度，不滿足SEA理論假設的基本前提。

(3)C板與D板的振動速度的FE-SEA混合法計算結果在中頻區與實驗值吻合的較好，整體誤差在3dB以內。且整個模型劃分為672個有限元單元，6個統計能量子結構，采用1.98 GHz的CPU臺式計算機的計算時間大約20 s，計算效率較FEM大幅度提高。

由Δ隨頻率的變化曲線可見：

(1)當結構中所有子系統的Δ≤1.5時，即特征長度小于3個半波長時，可統一采用FEM對結構整體分析；當所有子系統的Δ≥1.5，即特征長度可以容納至少3個半波長時，整體結構采用SEA進行分析；介于上述兩類情況之間的頻率區間，采用FE-SEA混合法進行處理。

(2)Δ隨頻率的變化曲線所反應的規律與圖9、圖10的對比結果基本符合，說明采用結構的特征尺寸D與波長λb的比值Δ作為劃分FEM、SEA、FE-SEA混合法的有效控制區是可行的。

(3)顯然在不同頻域內合理的選擇計算方法可以使誤差減小到最低限度，但是即使如此，來自實驗和數值計算的誤差仍然不可避免。其中一個主要原因在于結構的內損耗因子數量級相對較小，造成測量誤差較大。

4結論

設計了帶近似同質量的空心阻振質量與實心阻振質量的薄板結構模型，并分別采用FEM、SEA、FE-SEA混合法對其阻振性能進行數值計算和實驗研究，通過對板結構的振動速度數值解與實驗值對比，得到以下主要結論：

(1)近似同質量下的空心阻振質量的阻振效果在低頻區沒有實心阻振質量的好，但在中高頻區其傳遞損失逐漸凸顯，隨頻率呈上升趨勢，在大部分頻率下其阻振效果比實心阻振質量好，尤其在高頻區，阻振效果更加明顯。在分析頻率8kHz范圍內，空心阻振質量比實心阻振質量的整體阻振效果提高了10 dB左右。

(2)結構的特征尺寸D與波長λb的比值Δ隨頻率的變化曲線在雙對數坐標系下呈直線上升趨勢。當結構中所有子系統的Δ≤1.5時，即特征長度小于3個半波長時，可統一采用FEM對結構整體分析；當所有子系統的Δ≥1.5，即特征長度可以容納至少3個半波長時，整體結構采用SEA進行分析；介于上述兩類情況之間的頻率區間，采用FE-SEA混合法進行處理。

參考文獻

[1]張瑾，馬興瑞，韓增堯，等.中頻力學環境預示的FE-SEA混合方法研究[J].振動工程學報，2012,25(2):206-214.

ZHANG Jin, MA Xing-rui, HAN Zeng-yao, et al. FE-SEA hybrid method for the mid-frequency dynamic prediction[J]. Journal of Vibration Engineering, 2012,25(2):206-214.

[2]Langley R S, Bremner P. A hybrid method for the vibration analysis of complex structural-acoustic systems[J]. Journal of the Acoustical society ofAmerica,1999,105(3):1657-1671.

[3]Shorter P J, Langley R S. Vibro-acoustic analysis of complex systems[J]. Journal of Sound and Vibration,2005, 288:669-699.

[4]Che C D, Chen D S. Structure-borne sound attenuation in a multi-corner structure with attached blocking mass[J]. Journal of Ship Mechanics, 2010,14(9):1052-1064.

[5]王獻忠，孫龍泉，賈地，等. 含阻振質量基座的圓柱殼隔振特性[J]. 華中科技大學學報(自然科學版)，2012，40(5):50-53.

WANG Xian-zhong, SUN Long-qing, JIA Di, et al. Isolation characteristics of cylindrical shell with blocking mass base[J]. J. Huazhong Univ. of Sci. & Tech.(Natural Science Edition). 2012,40(5):50-53.

[6]申華，溫華兵，陸金銘，等. 空心方鋼阻振質量結構的阻振效果研究[J]. 中國造船，2013，54(1):101-107.

SHEN Hua, WEN Hua-bing, LU Jin-ming, et al.Research on the vibration isolation performances of hollow-square-steel vibration isolation mass structure[J]. Shipbuilding of China, 2013,54(1):101-107.

[7]趙松齡. 噪聲的降低與隔離[M]. 上海：同濟大學出版社，1985.