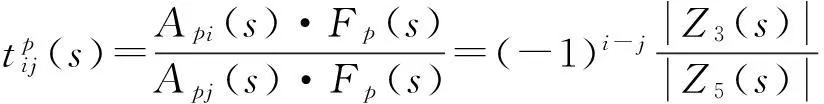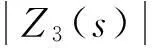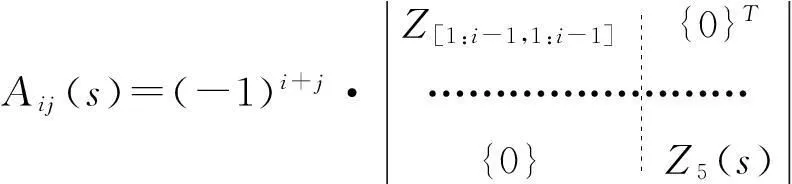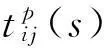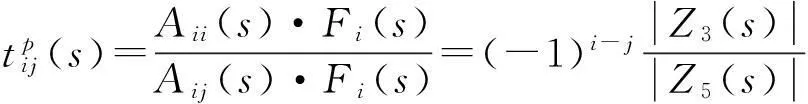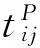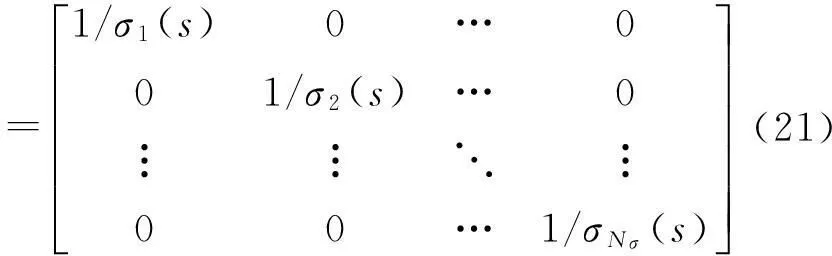多自由度系統中標量傳遞率的不變性及其應用

第一作者張昱男，博士生，1982年9月生

多自由度系統中標量傳遞率的不變性及其應用

張昱，朱彤，周晶

(大連理工大學海岸和近海工程國家重點實驗室，大連116024)

摘要：標量傳遞率函數描述了多自由度系統中兩個自由度的響應之間的關系，隨著應用范圍的延伸，近年來標量傳遞率逐漸受到了重視。本文從串聯系統出發，證明了多激勵作用下多自由度系統中標量傳遞率在某些條件下具有不變性，提出了該性質的統一的適用模型，并通過數值方法驗證了結論的正確性。在振動臺模型實驗中的應用表明，該性質可以在實際問題中起到指導作用。

關鍵詞：傳遞率；標量傳遞率函數；模態參數識別

基金項目：國家重點基礎研究發展計劃(973計劃)(2011CB013702);國家自然科學基金委創新研究群體基金(51121005)

收稿日期：2013-12-11修改稿收到日期：2014-04-30

中圖分類號:TB123文獻標志碼：A

Invariability of scalar transmissibility in a MDOF system and its application

ZHANGYu,ZHUTong,ZHOUJing(State Key Lab of Coastal and Offshore Engineering, Dalian University of Technology Dalian 116024, China)

Abstract:Scalar transmissibility attracting more and more attention in recent years describes the relationship between responses from two positions of one multi-degree of freedom (MDOF) system. The invariability of scalar transmissibility in a MDOF system under multiple loads was proved here, and the results were further extended to one unified model. A numerical test was performed to verify the correctness of the conclusion. Then, its application in a shaking table model test indicated that this property is helpful to dealing with practical problems.

Key words:transmissibility; scalar transmissibility function; modal parameter estimation (MPE)

經過60余年的發展，運行模態分析(Operational Modal Analysis，OMA)技術日臻成熟，目前的研究主要集中于解決一些具體的問題，源于白噪聲激勵假設的有色激勵問題即是其中之一[1]。Deviendt等[2-3]提出了一種獨特的基于傳遞率的OMA方法，這種方法不限制激勵的成分，是一種從根本上解決有色激勵問題的方案。

多自由度系統中的傳遞率分為兩類，一類描述兩個不同自由度的響應間的關系，稱作轉移函數(transmissibility function)[4]，偽傳遞率(pseudo-transmissibility)[5]，標量傳遞率(scalar transmissibility)[6]或直接傳遞率(direct transmissibility)[7]；另一類描述系統中不相交的兩個自由度集合間的關系，稱作多變量傳遞率(multivariable transmissibility)[6]，整體傳遞率(global transmissibility)[8]或簡稱為傳遞率(transmissibility)[9]。得益于在損傷識別[5, 10]，隔振[11]等領域中的廣泛應用，第二類傳遞率的性質得到了較為深入的研究，Ribeiro等[9, 12]提出了包括不變性在內的一些性質；相比之下對第一類傳遞率的研究非常有限。

Deviendt等[6, 13-15]提出的方法以第一類傳遞率為基礎，本文中稱其為標量傳遞率函數(Scalar Transmissibility Function，STF)。STF與模態參數間不存在直接的聯系，但如果不同荷載條件下相同兩點間的STF僅有有限個交點，則分析頻段內模態頻率的集合將是對應交點頻率集合的子集，這就是基于STF的OMA的理論基礎。顯然，基于STF的OMA適用的一個必要條件是不同荷載下相同兩點間的STF互異，因此在設計工況時必須避免工況改變但STF不變的情況出現，確實無法避免則必須選擇其它的OMA方法。對多自由度系統中STF不變性的研究，目前僅見于文獻[16]，Liu等以單激勵下的串聯系統作為研究對象，提出了三種形式的結構模型，證明在一定條件這些模型中的STF不隨激勵的變化而改變，并以數值算例驗證了結論的正確性。

本文以與文獻[16]不同的方式證明了STF的不變性在多激勵條件下同樣存在，并提出了該性質的統一適用模型；隨后通過數值算例驗證了該結論的正確性；在第三節中將該性質應用于振動臺模型實驗中，對實驗方案的選擇起到了指導作用；最后，對結論進行了簡練的總結。

1理論

多自由度系統的標量傳遞率函數(STF)tij(s)定義為

(1)

式中，s為拉普拉斯域變量；Yi(s)和Yj(s)分別為自由度i和j的運動響應(位移，速度或加速度)的拉普拉斯變換。分別稱自由度i和j為原點自由度和參考自由度。

系統的傳遞函數矩陣[H(s)]可表示為動剛度矩陣[Z(s)]的逆矩陣，即

(2)

式中，N是自由度的數量；adj([Z(s)])是[Z(s)]的伴隨矩陣；Aij是[Z(s)]關于第i行第j列元素的代數余子

式。[Z(s)]與系統的質量矩陣[M]，阻尼矩陣[C]和剛度矩陣[K]之間的關系為

(3)

可以將Yi(s)表示為如下的各自由度的激勵的加權和的形似

(4)

綜合式(1)和式(4)，得到

(5)

顯然STF只包含了系統某部分的零點信息，與作為整體性質的極點信息無關。

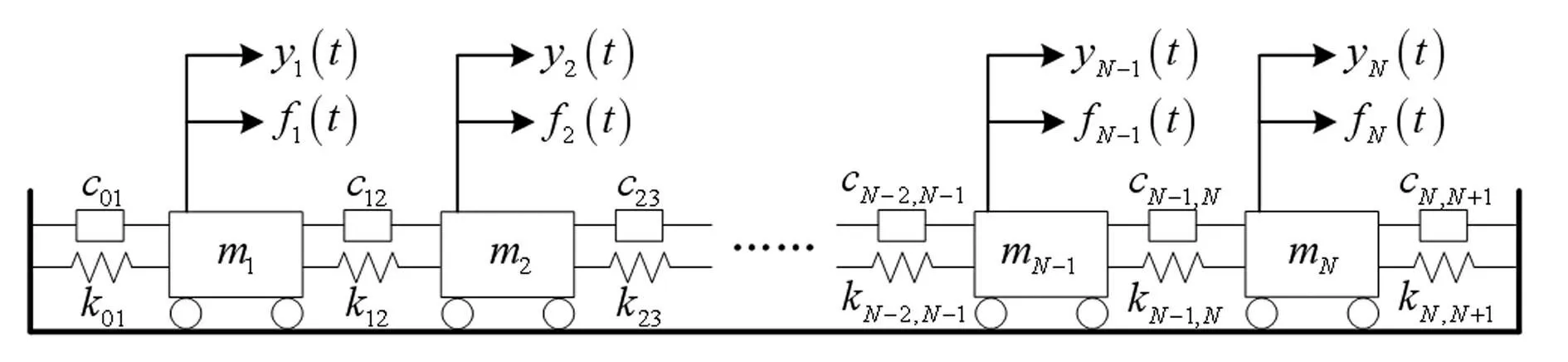
圖1　N自由度串聯系統 Fig.1 N-DOF series system

考慮如圖1所示的由集中質量，黏滯阻尼器和線性彈簧組成的N自由度串聯系統，系統的動剛度矩陣具有如下的三對角結構

(6)

其中，mi為第i個質量塊的質量，cij和kij分別為i、j兩個質點間的阻尼和剛度；ci和ki定義為

ci=ci-1,i+ci,i+1

ki=ki-1,i+ki,i+1

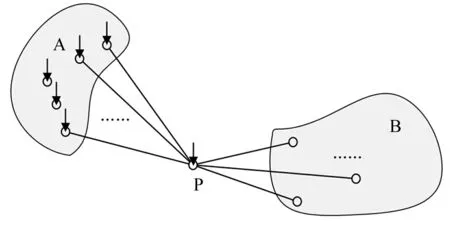
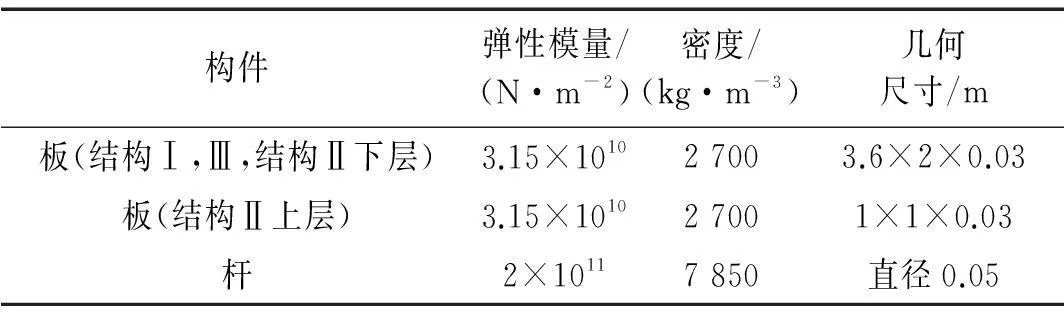
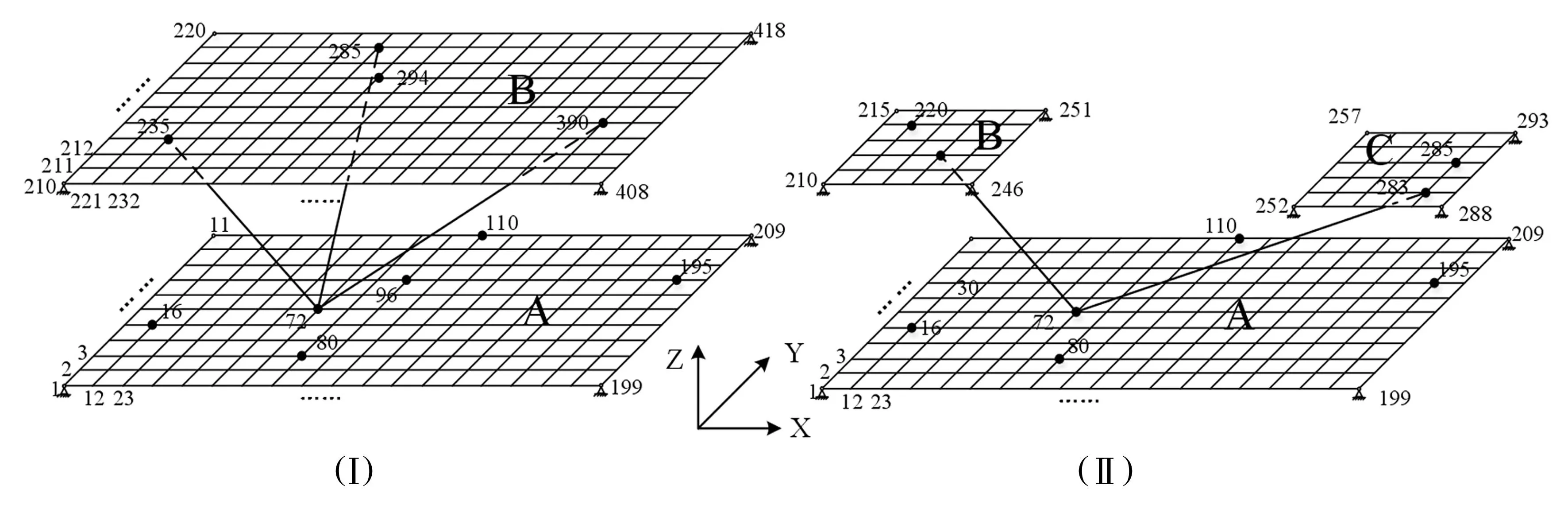
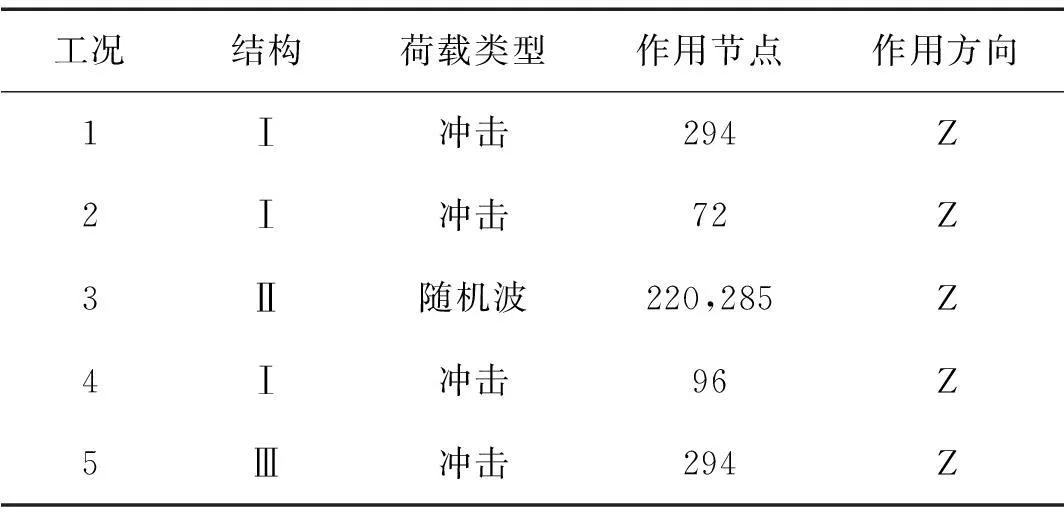
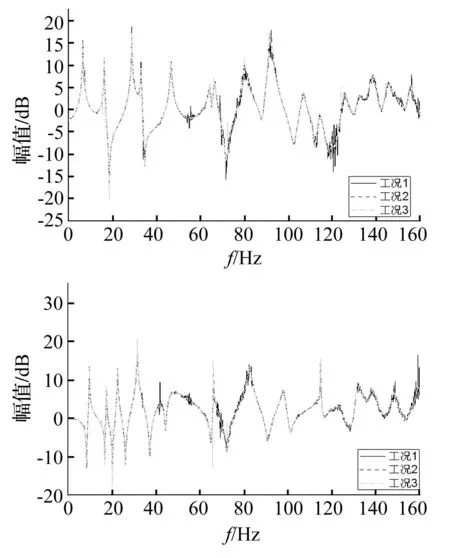
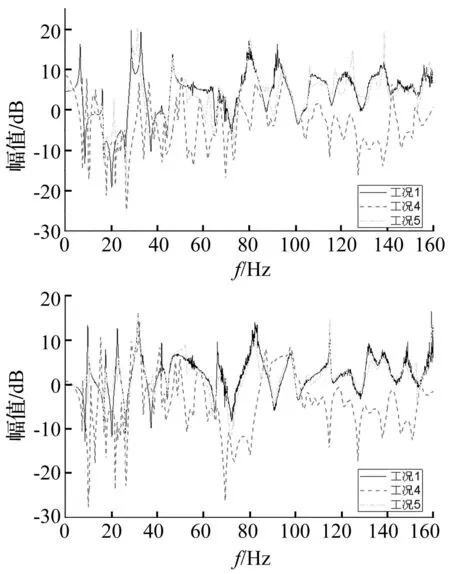
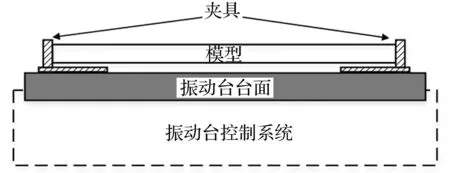
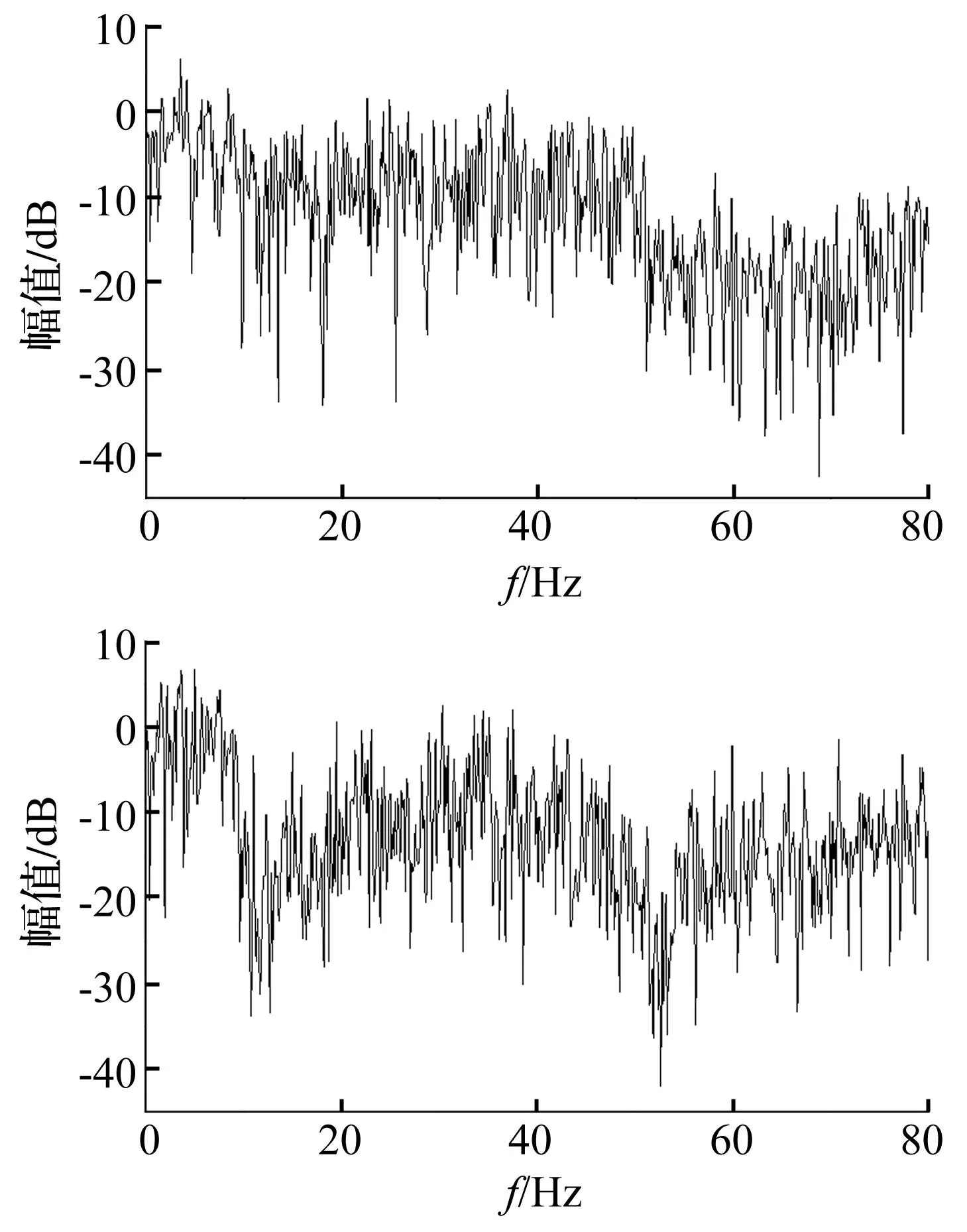
設p

(7)

(8)

式(7)和式(8)中的子矩陣[Z1(s)]~[Z5(s)]按如下方式定義

[Z3(s)]=[Z[i+1:N,i+1:N]]∈C(N-i)×(N-i)

(9)

式中，Z[i:j,k:l]表示由[Z(s)]的第i到第j行，第k列到第l列元素組成的子矩陣。假設系統中僅作用于自由度p的激勵不為零，將式(7)和式(8)代入式(5)中，得到

(10)

(11)

(12)

顯然，式(10)與式(12)的結果完全一致。通過相似的方式可以證明若i

如果系統是線性的，多個激勵共同作用下的結構響應將等于每個激勵單獨作用下結構響應的疊加。因此依次在自由度集合P={p1,p2,…,pn}中的每一個元素上施加荷載時系統的響應之和等于在這n個荷載共同作用下的結構的響應，即

(13)

(14)

根據前面的結論，如果P中的元素滿足max(p1,p2,…,pn)≤ min(i,j)或min(p1,p2,…,pn)≥ max(i,j)，有

(15)

將式(15)代入(14)中，得到

(16)

顯然，在如圖1所示的串聯系統中，只要非零激勵僅作用于某兩個自由度所圍區域的一側，這兩個自由度間的STF與激勵的數量和分布無關。

考慮到前面的討論中未規定自由度編號的規則，可以進一步將結論加以推廣：如果一個線性系統能夠劃分為如圖2所示的兩個子結構A和B，且A和B中任一自由度都至多與一個自由度p相聯系，則當激勵作用于A的自由度或p時，B中任意兩個自由度之間或者p與B中任意自由度之間的STF與激勵的數量，作用位置，大小，分布和屬性無關，僅由與子結構B的物理性質及p和B間聯系的屬性決定。

圖2　子結構示意圖 Fig.2 Substructures

2數值驗證

本節通過一組數值實驗驗證第1節中的結論。

考慮如圖3所示的兩個由板和桿組成的結構，所有的板均在四個角受到簡支約束，其參數如表1所示。結構Ⅰ的A、B板間距0.12m；結構Ⅱ的B、C板與A板的間距分別為0.12 m和0.06 m；結構Ⅲ與結構Ⅰ的區別僅在于將連接節點390和節點72的桿改為連接節點390和節點96。為了滿足僅有1個自由度關聯的前提，所有桿的端點都僅在Z方向與A板中的相應節點耦合。

表1　結構Ⅰ和結構Ⅱ中構件的參數

對結構Ⅰ~Ⅲ施加如表2所示的5種工況，其中工況3中作用于結構Ⅱ的不同節點上的隨機波互不相關。計算各工況中板A節點16到195，80到72的Z方向位移間的STF，t16,195，t80,72，所得結果如圖4和圖5所示。可以看到，在滿足前提條件的情況下，不同工況中板A的自由度間的STF是基本一致的，與激勵類型、數量和其它結構的形式無關。如果前提條件得不到滿足，雖然節點72與節點96位置非常接近，且結構Ⅲ中僅對一根桿進行了改動，但是不同工況中板A的自由度間的STF的變化是顯著的。需要說明的是，圖4中沖擊激勵下的STF中存在的某些“非一致”的震蕩是由如泄漏和加窗這樣的因素產生的，因為隨著信號截斷長度和指數窗衰減率的改變，這些震蕩的幅度也會發生變化，但整體的一致性趨勢卻不會隨之變化；另外，通過平穩的隨機響應計算得到的STF一般都不存在類似的問題，因此可以認為這些震蕩不是STF本身的差異。

圖3　結構Ⅰ和結構Ⅱ Fig.3 Structure Ⅰ & Ⅱ

工況結構荷載類型作用節點作用方向1Ⅰ沖擊294Z2Ⅰ沖擊72Z3Ⅱ隨機波220,285Z4Ⅰ沖擊96Z5Ⅲ沖擊294Z

圖4　工況1~3中的t 16,195(上) 和t 80,72(下) Fig.4 t 16,195 (top) and t 80,72 (bottom) from load condition 1~3

圖5　工況1，4，5中的t 16,195(上) 和t 80,72(下) Fig.5 t 16,195 (top) and t 80,72 (bottom) from load condition 1, 4 and 5

3實驗應用

本節中利用STF的不變性對實驗的方案進行選擇。

考慮如圖6所示的管線振動臺模型實驗系統，模型通過夾具固定在振動臺臺面上，水平向振動響應通過自南向北布設的10個加速度傳感器(H1~H10)捕捉。對于實驗設計和特征提取來說，模態參數數據都是必不可少的，考慮到實驗中管線將處于較為復雜激勵條件下，所以通過OMA技術獲取模態參數更為合適。

整個實驗系統可以劃分為如圖7所示的四個部分，實驗過程中振動臺控制系統驅動臺面運動，臺面再通過固定在其上的夾具將這種運動傳遞給模型。由于臺面的剛度和質量遠大于模型的，可以近似認為圖7中的實驗系統能夠表示為圖2所示結構形式，其中振動臺控制系統提供激勵，與振動臺臺面耦合的控制系統部件是子結構A，振動臺臺面和夾具相當于自由度b，將模型作為子結構B。這樣，無論振動臺以何種方式輸入平動激勵，在激勵的非零頻帶中模型在對應方向的響應都將保持不變，因此基于STF的OMA方法不適用于該類實驗，應該另選其它的分析方法。

圖6　管線振動臺模型實驗系統及水平向加速度測點 Fig.6 Vibration table test system of pipe model and acceleration measuring point of horizontal direction

圖7　振動臺模型實驗系統的組成 Fig.7 Components of vibration table model test system

這里基于文獻[15]中提出的虛擬頻響矩陣(virtual frequency response matrix)驗證上述判斷的正確性，下面簡略介紹文獻[15]中方法的原理。在Nl次互不相關的加載過程中，關于參考自由度j可以得到Nl(No-1)個STF，將這些STF關于每個復變量s組成矩陣[T(s)]，規模為(No-1)×Nl。[T(s)]的第i行第l列的元素是第l種荷載條件下自由度i到j間的STF，表示為tij(l)(s)。將[T(s)]進行奇異值分解，表示為

[T(s)]=[U(s)][Σ(s)][V(s)]H

(17)

奇異值矩陣[Σ(s)]是由Nσ=min(Nl,No-1)個以降序排列的奇異值組成的對角矩陣，表示為[Σ(s)]=diag(σ1(s),σ2(s),…,σNσ(s))，其中σ1(s)≥σ2(s)≥…≥σNσ(s)。

可以證明[2]，tij(l)(s)在系統極點s=λr處僅與對應模態在自由度i和j上的振型系數有關，表示為

(18)

因此，當s→λr時，矩陣[T(s)]將趨于如下的秩一矩陣

(19)

矩陣[T(s)]的偽逆可基于奇異值分解表示為

(20)

偽逆矩陣[Σ(s)]+是如下的由奇異值的倒數組成的對角矩陣

由于當s→λr時，[T(s)]除σ1外的其它奇異值都近似為0，所以

(22)

式中，c是不為零的常數。此時偽逆矩陣[T(s)]+的全部元素都將趨于無窮大，表示為

(23)

定義虛擬頻響矩陣[Hvirt(ω)]為[15]

[Hvirt(ω)]=[T(ω)]?

(24)

其中，ω是圓頻率變量。顯然，系統極點集合是[Hvirt(ω)]中元素的極點集合的子集。

圖8　由不同荷載下結構響應得到的虛擬頻響矩陣的 元素。上：第1行第1列元素；下：第2行第5列元素 Fig.8 Elements of virtual frequency response matrix from structure responses of different load conditions. top: element from row 1 column1; bottom: element from row 2 column 5

根據這一理論，基于振動臺先后分別輸入水平向白噪聲，EL-centro1940波，天津波時圖6中全部測點的加速度響應可以得到一系列規模為3行9列的虛擬頻響矩陣，其第1行第1列和第2行第5列的元素關于頻率的圖像如圖8所示。顯然，圖像中未包含顯著的模態信息。

4結論

綜上所述，本文的結論可以系統地表述如下：如果一個線性結構可以表示為如圖 2所示的子結構A-中間自由度p-子結構B的形式，則在激勵不為零的頻段中，子結構B中的STF具有如下的性質。

(1)子結構A中各自由度的質量或約束條件的變化不會對子結構B中的STF造成影響；

(2)子結構A中各自由度間的聯系屬性(剛度，阻尼)的變化不會對子結構B中的STF造成影響；

(3)如果系統中的激勵全部作用于子結構A，或自由度p上，在激勵不為零的頻段中子結構B中的STF或者自由度p與子結構B中自由度間的STF與激勵的數量，大小，分布和屬性無關。

本文中通過數值算例驗證了以上性質的有效性；在振動臺模型實驗中的成功應用表明，這些性質對處理實際的問題是有價值的，隨著針對標量傳遞率函數的研究的深入，這種價值也必然會得到越來越多的體現。

參考文獻

[1]Jacobsen N J. Separating structural modes and harmonic components in operational modal analysis[C]. IMAC XXIV,St. Louis, Missouri, USA,2006.

[2]Devriendt C, Guillaume P. The use of transmissibility measurements in output-only modal analysis[J]. Mechanical Systems and Signal Processing,2007,21(7):2689-2696.

[3]De Sitter G, Devriendt C, Guillaume P. Transmissibility-based operational modal analysis: Enhanced stabilisation diagrams[J]. Shock and Vibration,2012,19(5):1085-1097.

[4]Bendat J S, Piersol A G. 隨機數據分析方法[M]. 凌福根 譯. 北京:國防工業出版社,1976.

[5]Sampaio R P C, Maia N M M, Ribeiro A M R, et al. Damage detection using the transmissibility concept[C]. 6th International Congress on Sound and Vibration,Copenhagen, Denmark,1999.

[6]Devriendt C, De Sitter G, Guillaume P. An operational modal analysis approach based on parametrically identified multivariable transmissibilities[J]. Mechanical Systems and Signal Processing,2010,24(5):1250-1259.

[7]Maia N M M, Urgueira A P V, Almeida R A B. Whys and wherefores of transmissibility[A]. Beltran F. Vibration Analysis and Control-New Trends and Developments[M].Rijeka:InTech,2011:197-216.

[8]Urgueira A P V, Almeida R A B, Maia N M M. On the use of the transmissibility concept for the evaluation of frequency response functions[J]. Mechanical Systems and Signal Processing,2011,25(3):940-951.

[9]Maia N M M, Silva J M M, Ribeiro A M R. The transmissibility concept in multi-degree-of-freedom systems[J]. Mechanical Systems and Signal Processing,2001,15(1):129-137.

[10]顧建祖, 郝文峰, 駱英, 等. 基于固有模態函數振動傳遞率的結構損傷識別[J]. 建筑科學與工程學報,2011,28(1):27-32.

GU Jian-zu, HAO Wen-feng, LUO Ying,et al. Structural damage identification based on intrinsic mode function vibration transmissibility[J]. Journal of Architecture and Civil Engineering,2011，28(1):27-32.

[11]張春良, 鄭文, 梅德慶, 等. 復雜激勵環境下精密隔振系統的振動傳遞率研究[J]. 中國機械工程,2010,21(1):1-5.

ZHANG Chun-liang, ZHENG Wen, MEI De-qing,et al. Research on vibration transmissibility of vibration isolation system with complex vibration environment[J]. China Mechanical Engineering,2010，21(1):1-5.

[12]Ribeiro A M R, Silva J M M, Maia N M M. On the generalization of the transmissibility concept[J]. Mechanical Systems and Signal Processing,2000,14(1):29-35.

[13]Devriendt C, Guillaume P, De Sitter G, et al. Operational modal analysis by using transmissibility measurements with changing distributed loads[C]. 14th International Congress on Sound & Vibration,Cairns, Australia,2007.

[14]Guillaume P, Devriendt C, Vanlanduit S. Operational modal analysis in presence of unknown varying harmonic forces[C]. 14th International Congress on Sound & Vibration,Cairns, Australia,2007.

[15]Devriendt C, Weijtjens W, De Sitter G, et al. Combining multiple single-reference transmissibility functions in a unique matrix formulation for operational modal analysis[J]. Mechanical Systems and Signal Processing,2013,40(1):278-287.

[16]Liu W, Ewins D J. Transmissibility properties of MDOF systems[C]. IMAC XVI,Santa Barbara, California, USA,1998.