多輸入多輸出正弦掃頻試驗控制新方法

第一作者張步云男，博士生，1987年8月生

多輸入多輸出正弦掃頻試驗控制新方法

張步云，陳懷海，賀旭東

(南京航空航天大學機械結構力學及控制國家重點實驗室，南京210016)

摘要：研究了多輸入多輸出正弦掃頻試驗控制中信號發生、頻響函數估計和控制算法等關鍵問題。針對步進式正弦掃頻信號發生中因信號不連續而導致振動臺或激振器發生沖擊或損壞的問題，提出了兩個不同頻率的正弦信號平滑過渡的窗函數疊加延拓法，在滿足掃頻時間條件的同時也提高了試驗控制精度；以單位正弦掃頻信號作為激勵，改變不同激勵點的相位以產生滿秩激勵矩陣，運用相關積分法識別響應穩態正弦時域信號的幅值與相位，根據線性振動理論求解結構的頻響函數；以多個控制點的幅值為控制對象，推導出掃頻控制基本理論公式，通過參考值與反饋信號的比較來修正激勵信號以滿足試驗條件。以一懸臂梁為研究對象，建立了兩輸入兩輸出正弦試驗控制系統，結果表明該方法在掃頻控制中取得良好的效果。

關鍵詞：振動控制；掃頻系統；頻響函數估計；多輸入多輸出

基金項目：國家青年自然科學基金(11102083); 江蘇高校優勢學科建設工程資助項目

收稿日期：2013-10-21修改稿收到日期：2014-04-30

中圖分類號:O328文獻標志碼：A

New control method for MIMO swept-sine test

ZHANGBu-yun,CHENHuai-hai,HEXu-dong(State Key Laboratory on Mechanics and Control of Mechanical Structures,Nanjing University of Aeronautics & Astronautics, Nanjing, 210016, China)

Abstract:Swept-sine test is often used to simulate the real vibration situations of aircrafts, vehicles, watercrafts, and electronic devices. Here, a control method for the newly developed multi-input multi-output (MIMO) swept-sine test was proposed. A new method named overlapped windows and extension (OWAE) was proposed to smooth the discontinuous signal segments of two sinusoid waves with different frequencies. The method improved the control precision and met the requirement of swept time. The correlated integration method was used to identify amplitude and phase of a steady state sine signal. The structures’ frequency response functions (FRFs) were calculated with the linear time invariant (LTI) system theory. The swept control’s basic theoretical formulas with amplitudes and phases as control objects for a MIMO swept-sine test were derived. The excitation signal was updated by comparing the feedback response signal and the reference signal. An example was given to simulate a two-input two-output swept-sine control system. The results showed the validity of the proposed control method.

Key words:vibration control; swept-sine system; FRF estimation; multi-input multi-output (MIMO) system

正弦振動試驗是在實驗室中模擬真實環境中因振蕩、旋轉、脈動等產生的正弦振動，從而檢驗產品的可靠性與耐久性的一種環境試驗。因為正弦信號產生比較容易[1]，且在某些情況下可以代替復雜的隨機振動而降低試驗難度，所以用正弦信號作為振動試驗的激勵信號已成為振動試驗重要的一部分[2-4]。雖然正弦振動試驗理論及試驗技術已臻完善，但試驗中的一些關鍵問題如正弦信號的產生、控制系統的頻響函數估計等仍值得學者們深入研究。步進式正弦掃頻過程中，由于信號頻率的變化而產生的信號連接中斷會使振動臺產生沖擊，從而損壞振動臺或其它儀器設備。于慧君等[5]對前后兩段不連續信號采用加半正弦窗函數疊加處理方式，使信號平滑過渡。但是窗函數長度的選擇關系到處理效果，而且加窗后改變了原來信號的長度，不便于信號的發送。姜雙燕[6]在其博士論文中對正弦振動信號的連續發送和采集進行了研究，借鑒隨機振動試驗中時域隨機化生成純隨機信號法，采用加窗搭接的方法處理正弦信號。楊志東等[7]提出正弦控制試驗中信號綜合與分析的方法，初步解決掃頻信號的非穩態問題。牛寶良等[8]針對掃頻信號幅值處理的峰值法、均值法、均方根法、最小二乘法等需要整周期采樣的缺點，提出了變采樣率發送和采集信號，從而進行正弦振動控制試驗。但現有的儀器設備并不能滿足變采樣率的條件，故需研究新的試驗策略。本文提出窗函數疊加延拓方法在不改變采樣頻率和掃描時間的前提下，完成對不連續信號的平滑過渡，保證了設備的安全性。

為了取得好的控制效果，正弦振動試驗中系統頻率響應函數的精確估計起到關鍵作用。目前實驗室中采用正弦激勵、隨機激勵和錘擊法測量頻響函數。Gloth[9]在對步進式正弦信號激勵、多點正弦激勵、隨機激勵、脈沖激勵和掃頻激勵研究后選擇慢掃頻信號作為激勵，因為慢掃頻激勵可以對試件提供較大的推動力，并且可以節省測試時間。本文采用單元激勵，激勵矩陣由互不相關的列向量組成，在求頻響函數的時候可以直接進行求逆，而不用擔心出現病態頻響。文末以一懸臂梁為研究對象建立多輸入多輸出正弦振動試驗控制系統，驗證所提出方法的可靠性與有效性。

1正弦信號的產生與發送

1.1　基本公式

正弦振動試驗分為定頻試驗和掃頻試驗，掃頻方式有線性掃頻和對數掃頻兩種。掃頻試驗可分為快速掃頻和步進式掃頻，本文研究的即為步進式掃頻振動試驗。設一正弦信號為

x(t)=a(t)sinφ(t)

(1)

式中a(t)表示正弦幅值隨時間而變化，φ(t)是t時刻的相位。信號的頻率也是時間t的函數，如

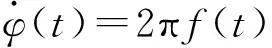
(2)

f(t)的單位為Hz，隨時間變化規律有如下兩種形式

(3)

式中:α為線性掃描率(Hz/s)，β是對數掃描率(otc/min)。設掃描起始頻率為fs，終止頻率為fe，掃描時間為T，則有

(4)

根據式(4)可知，fs、fe、T、α或β知其三可得第四個值。由式(1)~(4)可得到正弦信號的表達式

(5)

1.2　信號平滑連接

在正弦掃頻試驗中，信號的生成與發送問題至為關鍵。激勵信號中包含了頻率、幅值和相位三個要素，為了得到穩態的響應，必須使激勵信號持續一段時間。步進式正弦掃描的頻率不是連續變化的，需要在試驗之前按規定的掃描方式設定掃頻的頻率點。每個頻率的掃描時間相同，若有M個頻率點，總掃描時間為T，則頻率變化時間間隔為t=T/M，則在0，t，2t，…，(M-1)t時刻處，根據式(3)可得頻率值為f1，f2，f3，…，fM。

因每個頻率掃描周期相同，相鄰掃描信號間的連接會出現間斷的現象，如圖1所示。文獻[5]使用窗函數疊加的方法解決道路模擬試驗振動信號預處理過程中信號平滑連接問題。但是加窗重疊法減少了時域信號的長度，這在掃頻試驗中是無法滿足掃頻時間要求的。本文在此方法基礎上提出加窗重疊拓延法，保證信號平滑過渡的同時，還保證掃頻時間滿足試驗要求。設兩段信號分別表示為x1和x2，它們的頻率分別為fi和fi+1，幅值為ai和ai+1，它們的連接處如圖1所示。

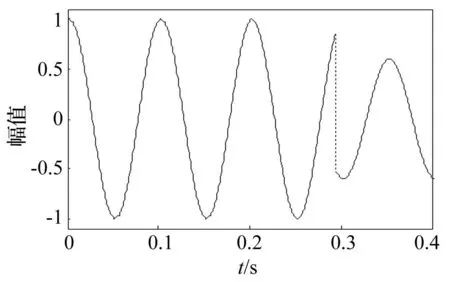
圖1　兩段不連續的信號 Fig.1 Two discontinuous signals

在信號處理過程中，采集信號后進行A/D轉換得到離散的時域信號。設信號采樣長度為N，則記兩段信號分別為x1(i)和x2(j)，i,j=1,2,…，N。記窗函數為w，其長度為n。自兩段信號過渡處分別向前、后取兩段長度為n/2的信號分別與窗函數的后半段、前半段相乘，然后再相加得到新的信號yk：

(6)

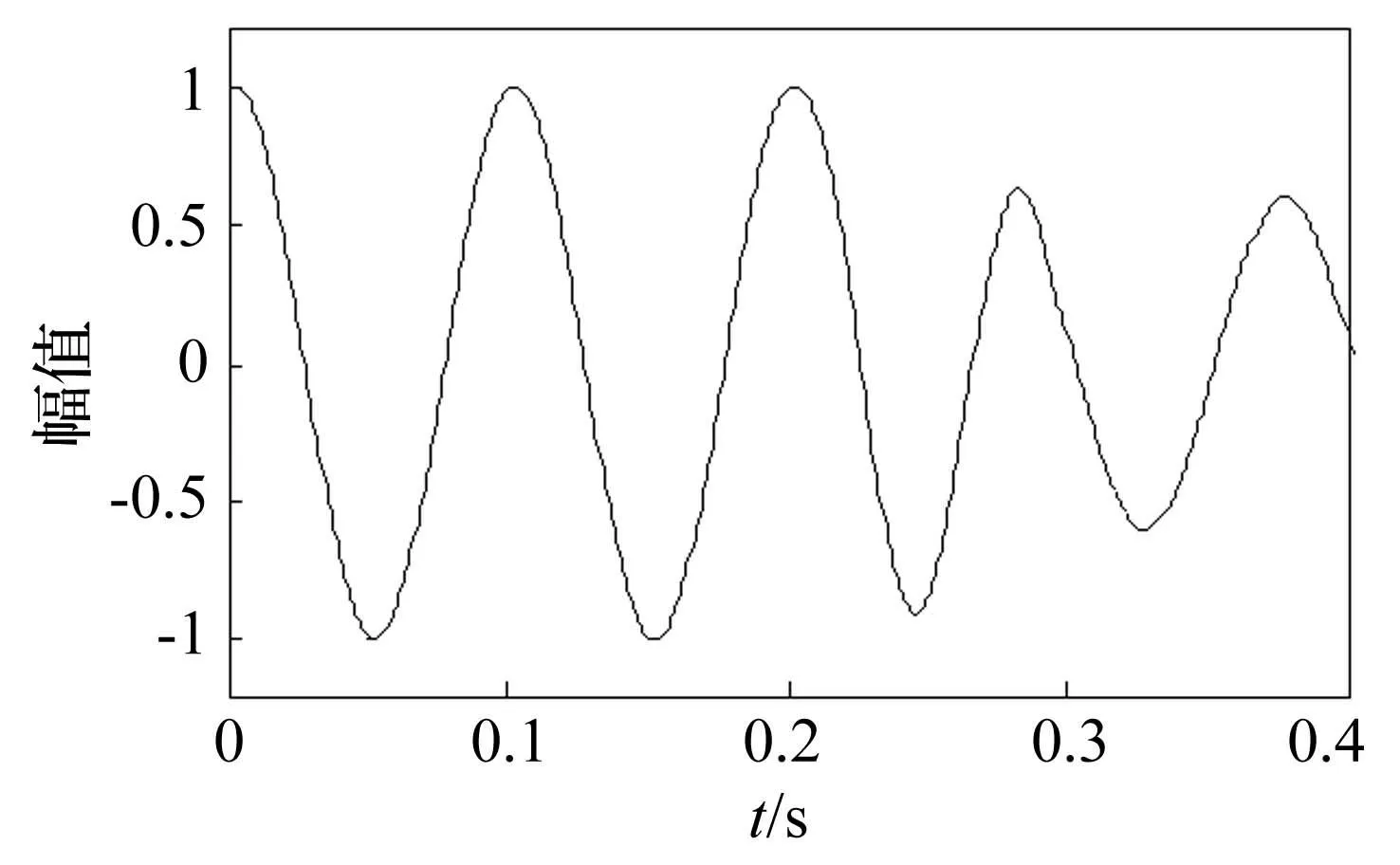
圖2　平滑過渡后的信號 Fig.2 Continuous signal

從圖2可以看出，經過處理后的信號在原間斷處變得平滑，但是x2的相位發生了改變，故本法對正弦振動的幅值控制精確，對相位控制則較差。

2多輸入多輸出正弦控制

2.1　相關積分法

相關積分法是一種時域中常用的信號處理方法，它能有效地抑制噪聲的影響，提高測試信號的信噪比。采用時域相關積分法識別正弦信號的幅值和相位，可以避免頻域計算法的泄漏問題。設采集一段時域信號u，經過A/D轉換為數字信號ui，信號長度為N，采樣間隔為t。已知正弦頻率為f0，其表達式可寫為

ui=Af0sin(2πf0·iΔt+φf0)

(7)

式中Af0表示待識別信號的幅值，φf0表示相位。計算ui和sin(2fiΔt)和cos(2fiΔt)的相關函數：

(8)

由此可以得到穩態正弦函數的幅值和相位分別為

(9)

式(8)~(9)即為相關積分法識別正弦信號幅值和相位的計算公式。此法識別精度高，計算簡單，運算速度快，適于實時振動試驗控制。在頻響函數估計中，需要用相關積分法識別響應信號的幅值與相位，與激勵信號的比即可得到頻響函數。

2.2　頻響函數

振動環境試驗中，頻響函數即為振動系統的數學模型，起到關鍵的作用，其測量和估計精度都會影響試驗控制效果。在多輸入多輸出振動試驗中測試頻響函數有多種方法，如利用隨機信號作為激勵同時測量多點的響應，根據H1、H2或Hv估計等方法估算頻響函數。這種方法簡單快捷，但是由于噪聲干擾的存在，導致估計結果不準確。本文采用多次掃頻激勵法估計頻響函數，雖然時間較長，但是可以得到更精確的頻響函數估計，對振動試驗控制的精度有顯著的提升。

對于多輸入多輸出振動系統，設有p個激勵點，l個響應點，頻響函數H是l×p的矩陣。若第一次激勵向量為d1=[d11d21…dp1]T，響應為u1=[u11u21…ul1]T，則激勵、頻響和響應的關系為

(10)

式中Hij是頻響矩陣H中的元素。由于頻響函數表征系統輸出與輸入的傅氏變換之比，對于穩態的正弦運動，傅氏變換即正弦信號在頻域的幅值與相位的組合。用相關積分法識別出響應的幅值與相位便能得到式(10)。

重復上述過程，用互不相關的p組激勵向量分別激勵，得到p組響應

u1=Hd1

u2=Hd2

?

up=Hdp

(11)

將式(11)聯立便可得到

(12)

即U=HD，U=[u1u2… up]稱為響應矩陣，D=[d1d2… dp]稱為激勵矩陣。因為d1，d2，…，dp互不相關，所以D是滿秩矩陣。由此可得頻響函數H為

H=UD-1

(13)

最簡單的激勵矩陣D為如下形式

(14)

即對角線及上三角的元素為1，下三角的元素為-1。1和-1表示激勵大小相同，方向相反，即相位相差為。用此單元滿秩矩陣作為激勵矩陣，使得計算更為簡單，也更容易實現。

2.3　控制方法

正弦振動試驗的流程如圖3所示。在試驗前先設定參考值r，參考值由幅值和相位組成；然后測試試件的頻響函數矩陣H，根據線性振動理論求得驅動信號d，加載到試件上后得到響應信號與參考值進行比較，得出誤差；再通過控制方法不斷修正驅動信號，直到響應滿足試驗條件要求。

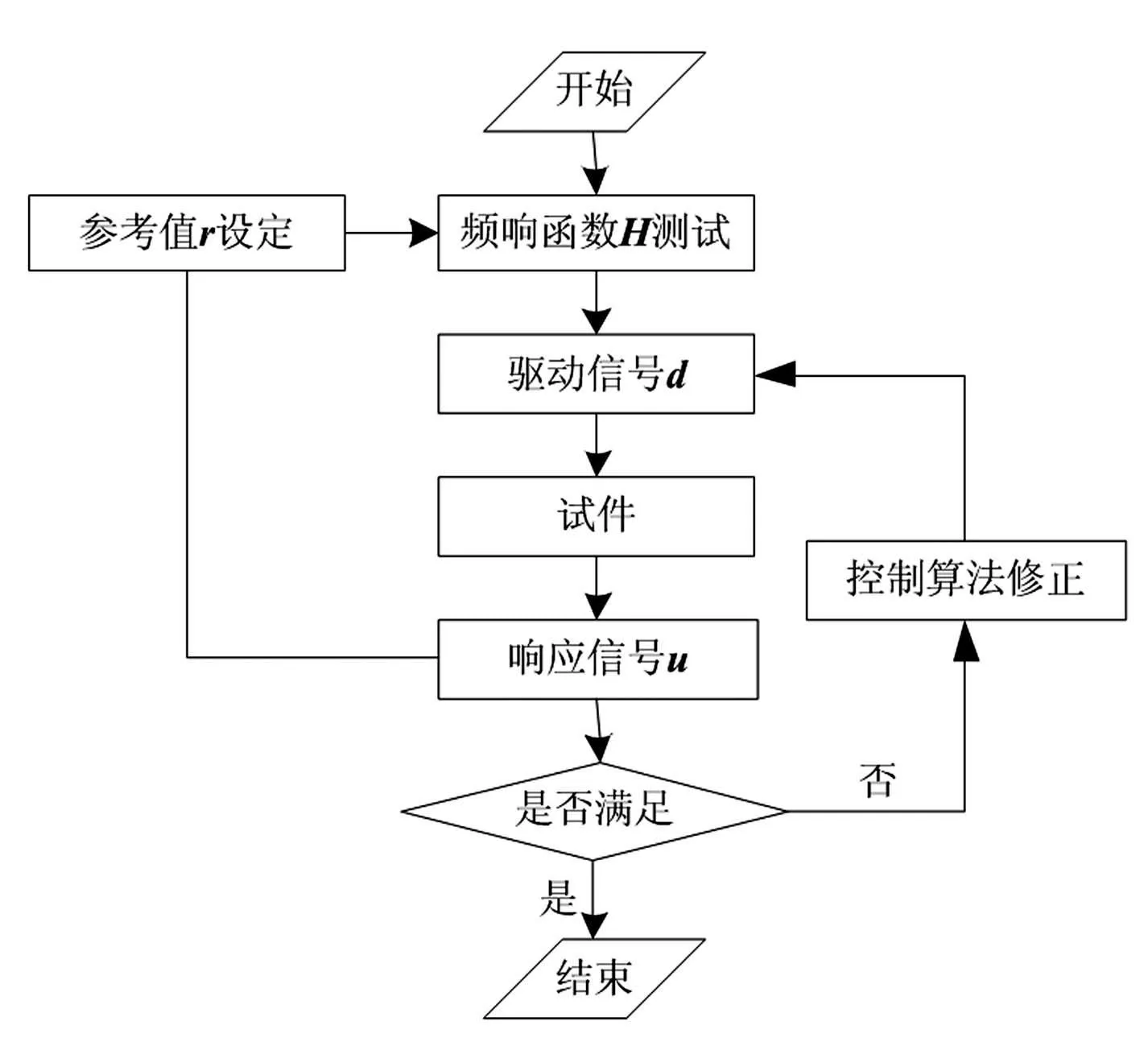
圖3　正弦控制流程圖 Fig.3 Folw digram of sine vibration control

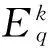
(15)

式中K表示修正因子，其大小決定收斂的精度與速度。

假設初始響應信號與參考值之比為1.1，取不同的K觀察響應收斂程度。分別取K為0.5，1，2，6，其收斂情況如圖4所示。

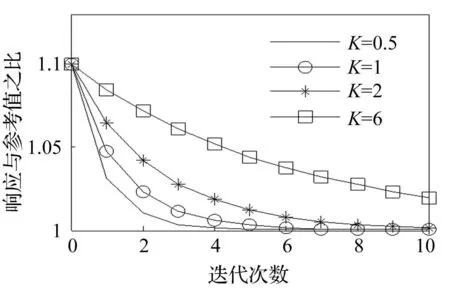
圖4　修正因子K對收斂速度的影響 Fig. 4 Effect of K on the rate of convergence

從圖中可以看出收斂速度與K大小成反比，K取值越小，收斂速度越快。

3試驗驗證

本文采用一懸臂梁作為試驗對象建立多輸入多輸出振動試驗系統。懸臂梁左端固定，試驗系統示意圖如圖5所示。梁的材料為不銹鋼，長度為1 115 mm，寬為50 mm，高為14 mm。兩個激振點分別布置在離懸臂端143 mm和376 mm處，控制點的位置也在這兩處，即對梁進行多輸入多輸出原點控制。

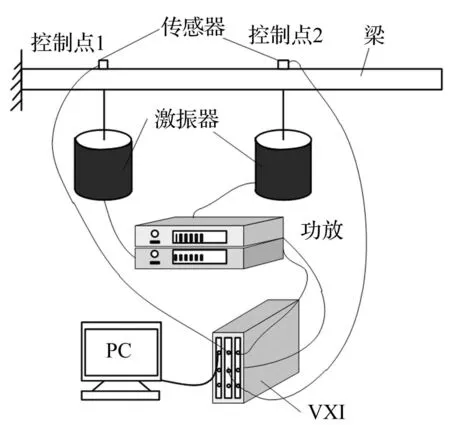
圖5　多輸入多輸出振動試驗系統示意圖 Fig. 5 Diagrammatic sketch of MIMO test system

試驗中采用Agilent VXI Plus & Play作為數據采集與發送儀器，兩臺Labworks PA-138功率放大器，兩個Labworks ET-139激振器，兩個PCB 333B32傳感器。試驗現場如圖所示。左圖為試驗總體布局，右上圖是VXI數據采集與發送系統，右下圖是激振器、懸臂梁和傳感器的布置。

圖6　振動試驗現場 Fig.6 Test scenes

根據振動環境試驗標準[2]，設置試驗參考值，見表1。掃描頻帶為10 Hz~2 000 Hz，在低頻區設置位移為目標值，中高頻區設置加速度為目標值。加速度與位移的換算關系為

(16)

式中，加速度A的單位為g，位移Z的單位為mm，頻率f的單位為Hz。

表1中設定了交越頻率點的參考值，位移與加速度相接的交越頻率點可以按照式(16)計算。設定好之后在對數坐標下進行線性連接即可獲得參考值的譜線。分別設定±3 dB為警報線，±6 dB為停止線。

按照2.2節中頻響函數估計方法，得到系統的頻響函數幅頻特性曲線如圖7所示。

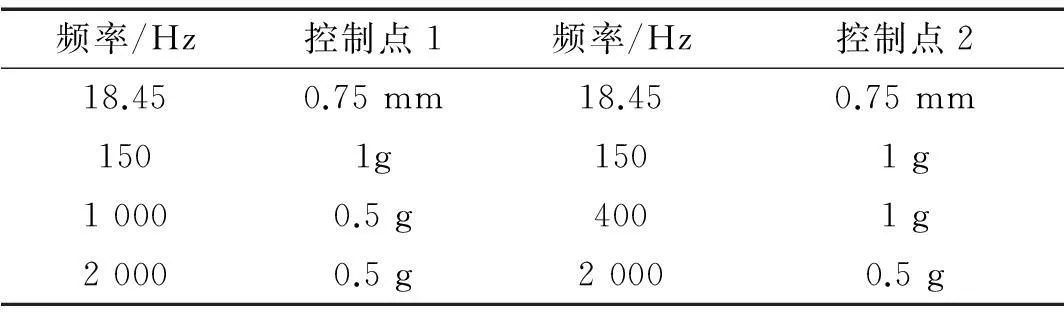
表1　MIMO控制參考值設置

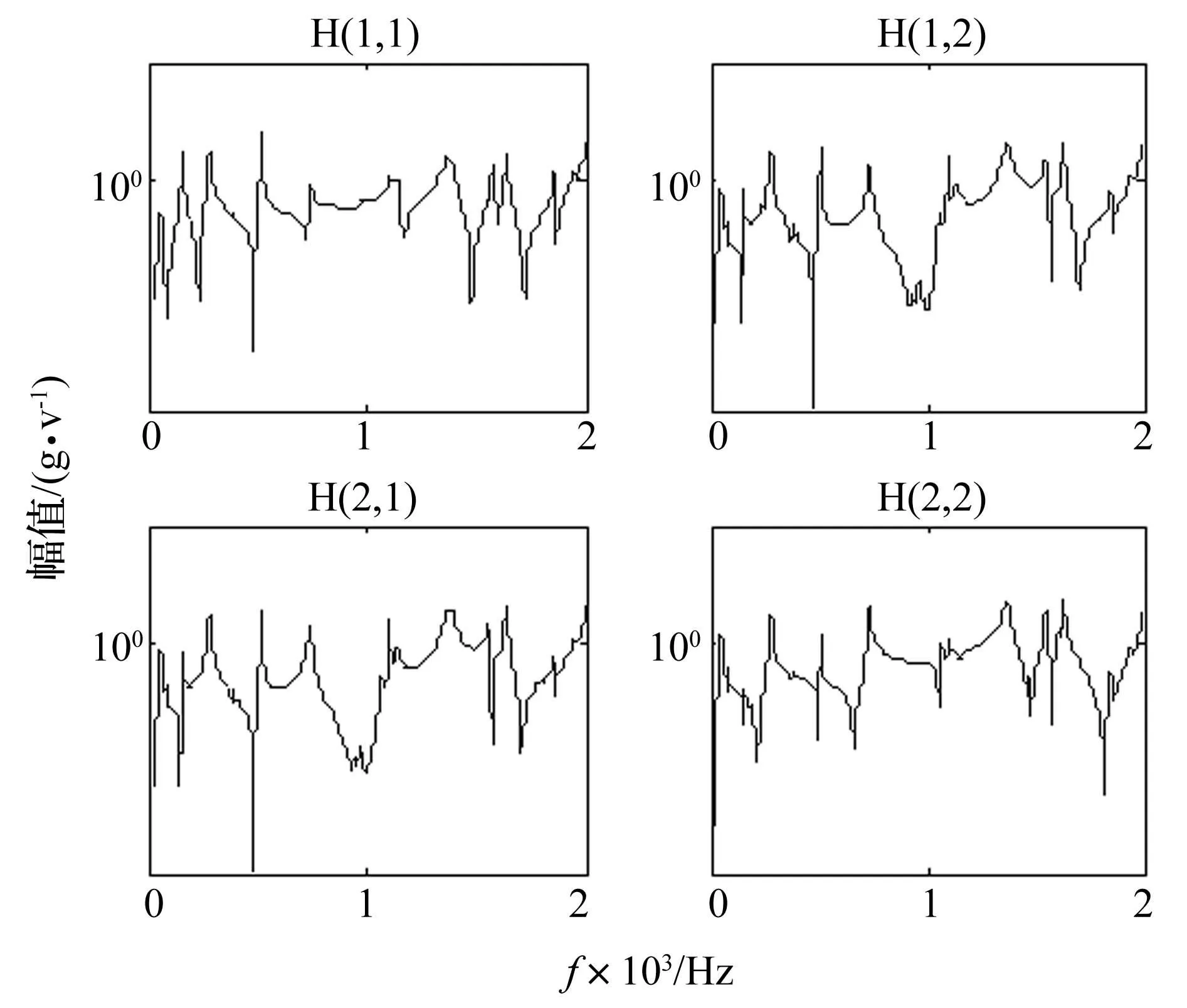
圖7　系統頻響函數幅頻曲線 Fig.7 Amplitude curves via frequency of FRF

按對數掃描方式從10 Hz開始進行正弦掃描，激勵信號的按照第2節的方法生成。從低頻到高頻掃描一次，控制兩個響應點的幅值，得到掃描結果如圖8和圖9所示。

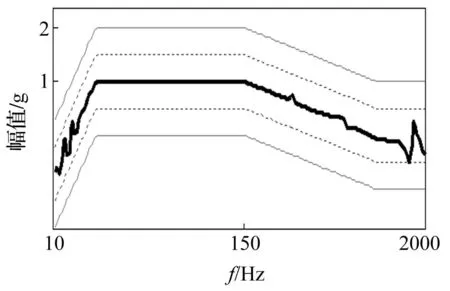
圖8　第1點控制結果 Fig.8 Control result of Point.1

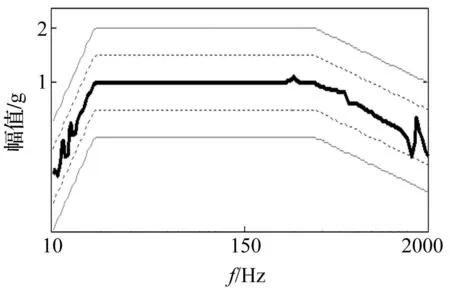
圖9　第2點控制結果 Fig.9 Control result of Point.2

從圖中可以看出兩點的響應幅值都已很精確地控制在參考值的容差范圍之內，在低頻和高頻部分有一些幅值的震蕩，但總的來說達到正弦掃描控制的試驗要求。

4結論

本文針對多輸入多輸出正弦振動控制系統中相關問題進行了深入的研究，討論了不連續信號的平滑過渡、頻響函數的估計和正弦振動控制算法等問題，最后通過建立MIMO振動試驗系統進行試驗。結果表明：

(1)本文所提出的窗函數疊加延拓法能夠平穩地處理不連續信號的過渡問題，在不改變采樣頻率的情況下保證了試驗的時間。

(2)文中所用的多次掃頻激勵法能精確地估計系統的頻響函數，保證了振動試驗控制的精確度。

(3)試驗結果表明本文提出的振動試驗方法切實可行。至于相位的控制，則需進一步研究。

參考文獻

[1]胡志強. 隨機振動試驗應用技術[M]. 北京：中國計量出版社，1998.

[2]Chinese PLA General Armament Department. GJB150.16A-2009, Laboratory Environmental Test Methods for Military Materiel[S]. 2009.

[3]夏益霖. 多點正弦模態試驗技術的注記[J]. 強度與環境, 1993,4:10-20.

XIA Yi-lin. Notes on the multiple-input modal testing technique with sine dwell excitation[J]. Structure & Environment Engineering, 1993,4:10-20.

[4]Thomas J R. Multi-frequency swept sine testing for automotive durability testing of engine mounted components[R]. SAE Technical Paper.

[5]于慧君, 陳章位, 王慶豐. 一種加窗重疊信號平滑連接方法及其在振動信號預處理中的應用[J]. 振動與沖擊, 2007,26(8):39-40.

YU Hui-jun, CHEN Zhang-wei, WANG Qing-feng. A signal smooth linking method and its application vibration signal pre-processing[J]. Journal of Vibration and Shock, 2007, 26(8):39-40.

[6]姜雙燕. 多軸向多激勵振動控制的研究與實現[D]. 南京：南京航空航天大學，2011.

[7]楊志東, 叢大成, 韓俊偉, 等. 正弦掃頻振動控制中的信號綜合與信號分析[J]. 振動工程學報, 2008,21(3):309-313.

YANG Zhi-dong, CONG Da-cheng, HAN Jun-wei, et al. Signal synthesis and analysis for swept-sine vibration control[J]. Journal of Vibration Engineering, 2008,21(3):309-313.

[8]Niu BL, Yan X. A FFT-based variety smpling-rate sine sweep vibration controller[C]// IEEE Int. Conf. Neural Networks & Signal Processing, Nanjing, Chian, 2003,12:14-17.

[9]Gloth G, Sinapius M. Analysis of swept-sine runs during modal identification[J]. Mechanical System and Signal Processing, 2004,18:1421-1441.