一題多解欣賞——第30屆全國中學生物理競賽復賽第2題評析

一題多解欣賞
——第30屆全國中學生物理競賽復賽第2題評析

陳東波

(紹興市上虞中學浙江 紹興312300)

收稿日期：(2014-06-10)

【題目】質量均為m的小球1和2，由一質量可忽略、長度為l的剛性輕桿連接，豎直地靠在墻角，小球1在桿的上端，如圖1所示．假設墻和地面都是光滑的，初始時給小球2一個微小的向右的初速度．問在系統運動過程中，當桿和豎直墻之間的夾角等于何值時，小球1開始離開豎直墻面？

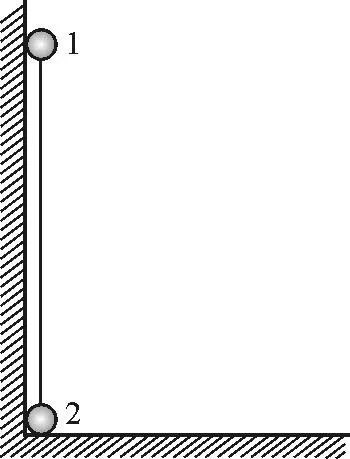
圖1

參考解答：如圖2，在小球1未離開豎直墻面之前，桿與豎直墻之間的夾角為θ時，小球1的坐標為

x1=0y1=lcosθ

(1)

小球2的坐標為

x2=lsinθy2=0

(2)

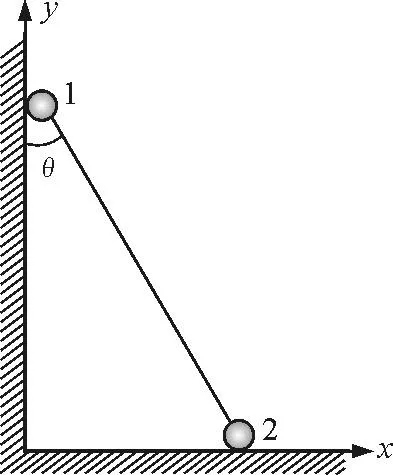
圖2

小球1 的速度為

(3)

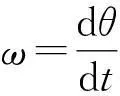
(4)

由機械能守恒定律，有

(5)

由式(5)得

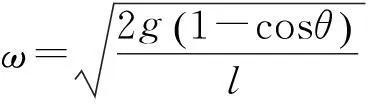
(6)

這里考慮到隨著時間t的增加，θ變大，因此

ω>0．

系統質心C的x坐標為

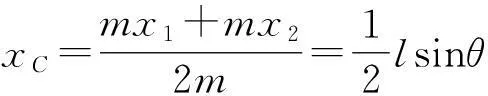
(7)

質心速度的x分量為

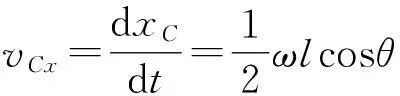
(8)

質心加速度的x分量為

(9)

由式(6)得

(10)

在得到上述結果時又利用了式(6)，把式(6)、(10)代入式(9)，得

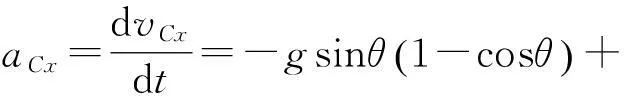
(11)

設豎直墻面對小球1的正壓力為T，質心C在x方向上的運動滿足

T=2maCx

(12)

由式(12)可知，當aCx=0時，T=0.

此時，小球1開始離開豎直墻面，且θ=0為運動的初始時刻，即可得

此即小球1離開豎直墻面時，桿與墻面的夾角．

另解1

假設小球1被某種水平外力T束縛，使其只能在豎直平面內運動，則當桿與豎直墻面夾角為θ時，小球1與小球2的速度在沿桿方向的分速度必然有

v1cosθ=v2sinθ

由機械能守恒定律可得

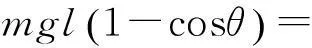
由系統牛頓運動定律，小球1在水平方向所受合外力為零，則系統在水平方向所受合外力為

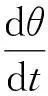
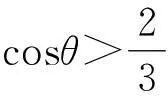
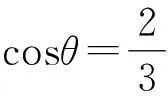
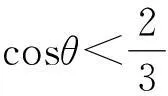
另解2

現假設墻面對小球1的彈力為T1，此時小球1沿豎直平面運動，水平方向合力為零，輕桿彈力必為

小球2沿水平平面運動，則水平地面對小球2的支持力為

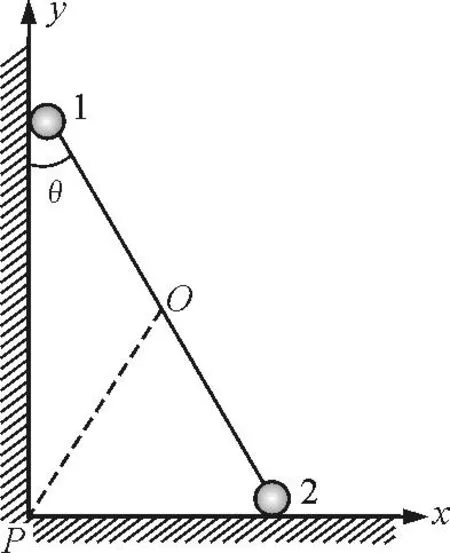
圖3

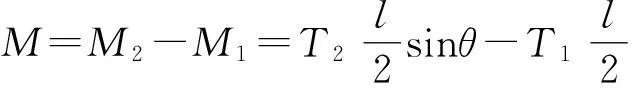
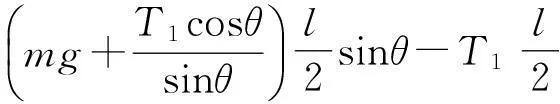
可得系統繞O轉動的角加速度為

上式整理可得

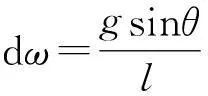
左右都乘以ω

考慮到在零時刻，ω和θ都為零，則有

在小球1離開墻面之前，考慮到直角三角形的中線性質，OP與豎直墻面的夾角始終等于輕桿與豎直墻面的夾角，則O點運動的角速度與角加速度大小都等于輕桿轉動的角速度與角加速度的大小，則可以得到O的法向加速度與切向加速度分別為

當小球1離開墻面時，系統在水平方向不受外力，O點在水平方向加速度為零，即

a//=ansinθ-atcosθ=

化簡可得

另解3

如另解2分析，O點運動的角速度大小等于輕桿轉動的角速度ω，則有機械能守恒定律及柯尼系定律可得

可得O點運動所需向心力為

這個力等于系統所受重力、墻面彈力、地面彈力在沿OP方向分力的矢量和．再利用另解2中墻面彈力、地面彈力的關系可得

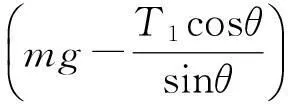
即

因為墻面彈力T1取負值不合題意，故可得答案．