物理建模能力培養(yǎng)的實(shí)踐探索*——從劍橋大學(xué)一道彈性碰撞測(cè)試題談起

物理建模能力培養(yǎng)的實(shí)踐探索*①
——從劍橋大學(xué)一道彈性碰撞測(cè)試題談起

張紅洋馬小虎

(陜西師范大學(xué)物理學(xué)與信息技術(shù)學(xué)院陜西 西安710062)

*陜西省教育科學(xué)規(guī)劃課題“基于課堂教學(xué)案例促進(jìn)教師專業(yè)發(fā)展的研究”,項(xiàng)目編號(hào)：SGH13061；陜西師范大學(xué)基礎(chǔ)教育課程中心 “基于課堂視頻案例促進(jìn)教師專業(yè)發(fā)展研究”的研究成果,項(xiàng)目編號(hào)：JCJY201007

摘 要：以劍橋大學(xué)一道彈性碰撞測(cè)試題為例，分析、討論了在大學(xué)物理教學(xué)中如何培養(yǎng)學(xué)生的物理建模能力等問題.

關(guān)鍵詞：彈性碰撞建模能力培養(yǎng)物理模型

作者簡(jiǎn)介：張紅洋(1973-)，男，博士，副教授，碩士生導(dǎo)師，主要從事大學(xué)物理教育研究.

收稿日期：(2015-04-29)

1問題的引出

對(duì)教學(xué)活動(dòng)有效性的追求是教育永恒的主題之一.建模是人類認(rèn)知和科學(xué)探究的基礎(chǔ)，是一種能夠有效激發(fā)、支持和評(píng)估學(xué)習(xí)者概念轉(zhuǎn)變的強(qiáng)有力的策略.物理教學(xué)活動(dòng)中,對(duì)學(xué)生建模能力的重視和培養(yǎng)，將會(huì)為學(xué)生學(xué)習(xí)和教師教學(xué)提供新的動(dòng)力和支持.建模可以幫助學(xué)生把自己的思維表達(dá)出來并外顯化，使其隱性的思維過程可視化并得到檢驗(yàn)，從而可使學(xué)生進(jìn)行有意義的學(xué)習(xí).

劍橋大學(xué)為了檢驗(yàn)學(xué)生的學(xué)習(xí)質(zhì)量和教學(xué)的有效性，曾設(shè)計(jì)了一套題目測(cè)試學(xué)生的物理建模能力，僅有30%的學(xué)生能夠正確解答，結(jié)果很不理想[1].筆者在教學(xué)實(shí)踐中，曾用這些題目對(duì)陜西師范大學(xué)物理專業(yè)的3屆大學(xué)三年級(jí)的學(xué)生進(jìn)行測(cè)試，發(fā)現(xiàn)學(xué)生對(duì)這些問題難以正確地分析和解決，究其原因，這些題目均需要學(xué)生能從題目描述的物理情境中抽象并構(gòu)建出合適的物理模型，而傳統(tǒng)的物理教學(xué)則對(duì)學(xué)生的建模能力沒有足夠重視.

下面以劍橋大學(xué)一道物體碰撞的題目為例，做些討論分析.

【題目】如圖1所示,乒乓球和高爾夫球(乒乓球在高爾夫球上面)同時(shí)從距地1 m高的地方自由下落，請(qǐng)問乒乓球會(huì)彈起多高？

圖1

要解決這個(gè)題目，首先需要從真實(shí)的實(shí)際問題情境中構(gòu)建出正確的物理模型.物理模型是人們?yōu)楦媒沂臼挛锉举|(zhì)和內(nèi)在特性而建立起的一種簡(jiǎn)化模型.建模能力是物理學(xué)習(xí)的核心能力之一，也是學(xué)生解決實(shí)際問題的重要途徑和方法[2].

2運(yùn)用動(dòng)量守恒定律和能量守恒定律求解

建模1：將實(shí)際情境中的高爾夫球和乒乓球進(jìn)行理想化建模，作為理想剛體，并根據(jù)其質(zhì)量特點(diǎn)，認(rèn)為高爾夫球的質(zhì)量遠(yuǎn)遠(yuǎn)大于乒乓球.

建模2：將其碰撞過程和作用過程(球與地面的作用過程和高爾夫球與乒乓球的作用過程)建模為理想化碰撞過程，即其過程中動(dòng)量和能量守恒.

設(shè)高爾夫球的質(zhì)量為M，乒乓球的質(zhì)量為m.由于高爾夫球的質(zhì)量遠(yuǎn)遠(yuǎn)大于乒乓球的質(zhì)量，即M?m，當(dāng)高爾夫球與地面碰撞后(此碰撞過程較易理解，在此不做討論)以大小不變的速度跳起時(shí)，兩球以方向相反、大小相同的速度v0做完全彈性的對(duì)心碰撞，如圖2所示[3].

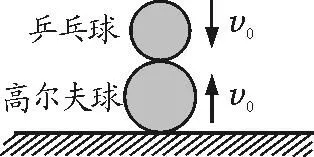
圖2

設(shè)兩球相互碰撞后高爾夫球的速度為v1，乒乓球的速度為v2，并規(guī)定豎直向上為正方向，如圖3所示.

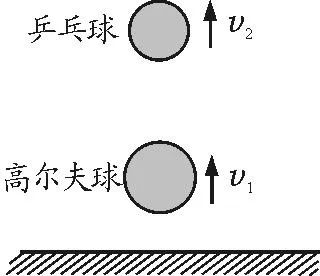
圖3

由題意可得

Mv0-mv0=Mv1+mv2

(1)

(2)

由式(1)和(2)聯(lián)立求解得出

又因?yàn)镸?m，容易得出碰撞后高爾夫球的速度v1=v0，而乒乓球的速度v2=3v0,根據(jù)位移-速度公式

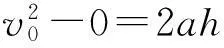
(3)

得乒乓球從高度h=1 m落至地面時(shí)的速度為v0

(4)

根據(jù)動(dòng)量能量守恒得，當(dāng)乒乓球經(jīng)彈性碰撞速度方向向上時(shí)，速度大小為3v0，根據(jù)式(3)得

(3v0)2=2gh1

(5)

由式(4)和式(5)得

h1=9h

(6)

不難得出，乒乓球碰撞后彈起高度為9 m.

這種解法的關(guān)鍵是構(gòu)建動(dòng)量與能量守恒模型.能量與動(dòng)量都是物體運(yùn)動(dòng)量的量度方式.在研究小球碰撞問題時(shí)，該系統(tǒng)只在碰撞物體間內(nèi)力的相互作用下，當(dāng)一種運(yùn)動(dòng)轉(zhuǎn)化為另一種運(yùn)動(dòng)形式時(shí),一方面能量發(fā)生傳遞與轉(zhuǎn)化,同時(shí)在另一方面也必伴隨著動(dòng)量的傳遞與轉(zhuǎn)化,而且它們都遵循各自的守恒定律.因此當(dāng)把問題轉(zhuǎn)換為模型時(shí)，只需考慮守恒問題[4].

3運(yùn)用彈性碰撞模型和參考系轉(zhuǎn)換方法求解

這種解法的總體思路是：通過對(duì)物理碰撞過程的情景分析，構(gòu)建多個(gè)物理碰撞模型，并靈活運(yùn)用參考系變換方法，將抽象復(fù)雜的物理問題轉(zhuǎn)換成簡(jiǎn)單具體的物理模型，從而實(shí)現(xiàn)不用復(fù)雜的數(shù)學(xué)公式和計(jì)算，高屋建瓴地解決問題，體現(xiàn)物理思想與方法的博大精深.

知識(shí)準(zhǔn)備與模型構(gòu)建1：小球以速度v0運(yùn)動(dòng)，如圖4(a)所示，與墻碰撞后，該小球會(huì)以方向相反，大小與v0相同的方式運(yùn)動(dòng)，如圖4(b)所示.

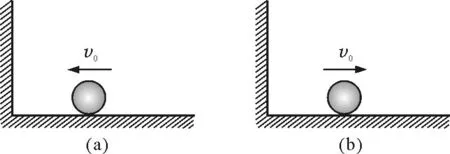
圖4

知識(shí)準(zhǔn)備與模型構(gòu)建2：若球A的質(zhì)量mA遠(yuǎn)遠(yuǎn)大于球B的質(zhì)量mB，小球A,B速度大小均為v0，相向而行.若以A為參考系(參考系轉(zhuǎn)換)，則B的速度為2v0，相撞后A的速度可視為不變(因?yàn)閙A遠(yuǎn)遠(yuǎn)大于mB)，而球B則會(huì)以2v0的速度與初始運(yùn)動(dòng)方向相反的方向運(yùn)動(dòng).再通過參考系轉(zhuǎn)換將球A參考系轉(zhuǎn)換為地面參考系，則可以得出球B的速度為3v0，如圖5所示.

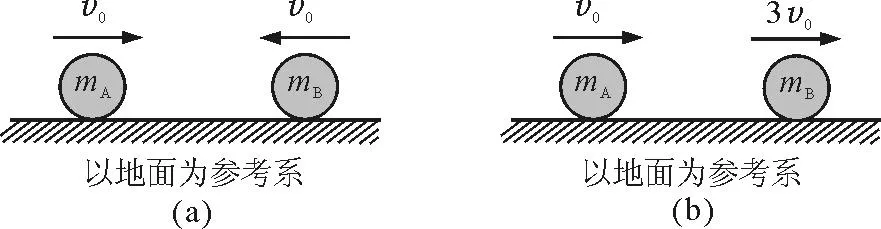
圖5

基于以上兩方面的知識(shí)準(zhǔn)備與模型構(gòu)建，本問題的解決過程如下.

高爾夫球和乒乓球的彈性較強(qiáng)，故在本研究中，可以將其視為理想彈性物體，其每一次碰撞過程均被視為完全彈性碰撞過程，當(dāng)乒乓球和高爾夫球從距地1 m處同時(shí)落下，到達(dá)地面時(shí)有相同的速度v0，如圖6所示.

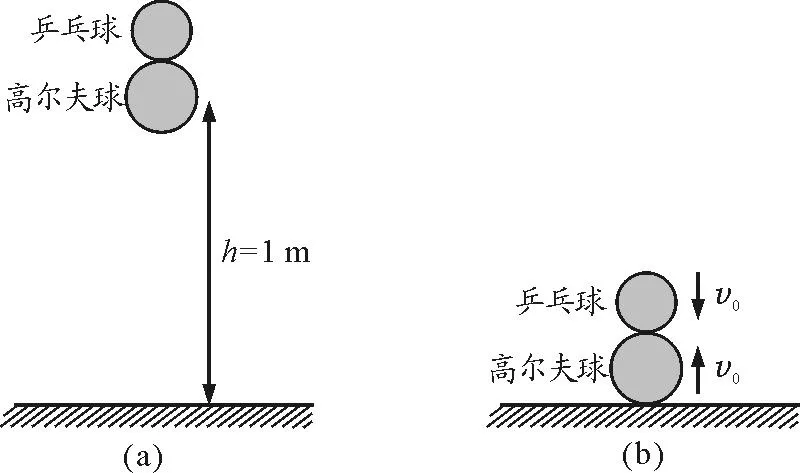
圖6

高爾夫球的質(zhì)量遠(yuǎn)遠(yuǎn)大于乒乓球，高爾夫球擊地后以與初速度大小相等,方向相反的速度向上彈回，故和知識(shí)準(zhǔn)備與模型建構(gòu)2相似.高爾夫球相當(dāng)于球A，乒乓球則相當(dāng)于球B.可得乒乓球在碰撞后的速度為3v0，如圖7所示.

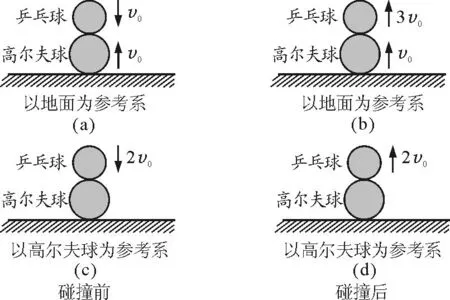
圖7

根據(jù)式(1)～(4)可得乒乓球彈起的高度是9 m.

該解法的關(guān)鍵在于構(gòu)建不同參考系下的物理模型，通過選好參考系，使解題思路更為簡(jiǎn)潔、清晰，使解題過程更為簡(jiǎn)單、自然[5].通過構(gòu)建簡(jiǎn)化的運(yùn)動(dòng)模型，探究小球在不同參考系下的運(yùn)動(dòng)狀態(tài)，掌握不同參考系之間的內(nèi)在聯(lián)系，實(shí)現(xiàn)參考系之間的數(shù)量變換，達(dá)到解決問題的目的.

4小結(jié)

以上兩種解法，解題方法雖存在差異，但正確構(gòu)建物理模型則貫穿于問題解決的核心過程.很多學(xué)生不能把題目中的對(duì)象和過程簡(jiǎn)化成理想的物理模型，仍然按常規(guī)邏輯思考，陷入如下誤區(qū)，一是摩擦力做功可否忽略，二是兩者質(zhì)量關(guān)系不知道，用功能關(guān)系求解時(shí)有障礙，想用動(dòng)量、能量方面的知識(shí)求解，卻感覺無從下手.這個(gè)問題并不是為了讓學(xué)生認(rèn)為高爾夫球的質(zhì)量相對(duì)于乒乓球的質(zhì)量來說是無窮大的.一些學(xué)生在答題紙上寫道：?jiǎn)栴}的答案取決于(它們的)重量.有的學(xué)生認(rèn)為兩個(gè)球在下落之前是并排放置的(而不是一上一下).由此可見，學(xué)生不能正確解答的重要原因在于不能通過題目中對(duì)物理情境的描述建立合適的物理模型.

因此建立正確、合理的物理模型，能透過現(xiàn)象識(shí)別和發(fā)現(xiàn)模型是解題的關(guān)鍵所在[2].從這個(gè)題中可以看到，英國(guó)物理教育重在通過實(shí)驗(yàn)探究，利用形象、生動(dòng)的模式，指導(dǎo)學(xué)生怎樣去認(rèn)識(shí)、分析、解決問題，通過總結(jié)、概括，進(jìn)而提升到教會(huì)學(xué)生物理思想和物理方法的教育理念.

參 考 文 獻(xiàn)

1Sanjoy Mahajan,David MacKay. Physics Teaching.http://www.inference.phy.cam.ac.uk/teaching/survey,2014

2陳淑萍．教會(huì)學(xué)生用物理模型思考問題．物理教師，2012.33(3)

3曹磊，譚樹杰.各國(guó)物理教學(xué)改革剖析.上海:上海教育出版社,1996.207～209

4王光裕．關(guān)于動(dòng)量守恒與能量守恒問題．南京工業(yè)大學(xué)學(xué)報(bào)(自然科學(xué)版)，1981,36(5)：103～109

5沈亮. 轉(zhuǎn)換參考系巧解物理問題.中學(xué)物理,2013,31(11) : 88～89